Dans cette page, on a présenté le modèle 3D de la géométrie euclidienne sur une sphère épointée. C’est aussi, au sens de Bolyaï et Lobatchevsky, une horisphère pour la géométrie hyperbolique, et donc travailler ce modèle, même si on reste dans une géométrie euclidienne, a du sens pour l’appropriation de la géométrie hyperbolique.
Cet article propose au lecteur de construire quelques figures élémentaires sur l’horisphère avec des macros structurées dans les dossiers suivants :

Dans un premier temps, on utilisera surtout les deux premiers dossiers, le troisième nécessitant une pratique plus régulières du logiciel. Dans tous les cas, les objets à montrer dans les macros sont toujours des points, y compris pour les droites.
Comme l’intersection de deux droites se fait par la données de deux points constituants de cette droite, les macros qui renvoient des droites renvoient aussi des points de ces droites. C’est en particulier le cas de la médiatrice qui renvoie aussi le milieu des deux points et un autre point.
Conjugaison. Les 1 sont la projection stéréographique et son retour. On l’utilisera pour des constructions affines. Les 2 échangent la sphère et l’écran du logiciel pour travailler directement en euclidien.
Cercle Alt uA prend un point sur le segment [SN] et renvoie une latitude pour y placer un point.
La figure proposée contient déjà 4 points et 5 droites que l’on peut cacher, ainsi que les projections utiles pour les conjugaisons (que l’on peut cacher bien entendu)
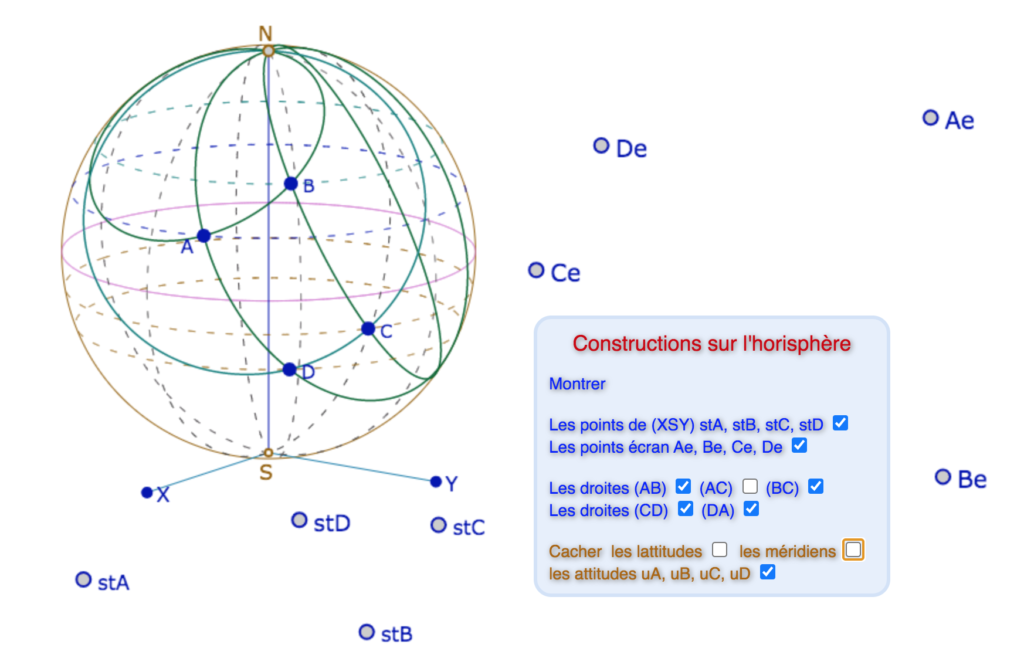
La macro Cercle 3 pts est significative des subtilités que l’on peut rencontrer parfois dans les modèles : elle permet de construire des Hori-cercles car ce sont des cercles euclidiens. Mais comme la Hori-droite passant par deux points A et B est le cercle euclidien passant par A, B et N, cette macro permet aussi de construire les Hori-droites.
Rappels : il faut être en mode consultation (aucun outil actif) pour piloter la sphère au doigt ou à la souris, et être en monde standard (flèche gauche sélectionnée) pour pouvoir créer des objets, et bien entendu en mode macro pour les utiliser.
Préférer ouvrir cette figure dans un nouvel onglet, ou encore télécharger le fichier
Quelques pistes de constructions possibles
En géométrie affine : on peut chercher à construire des figures autour des parallèles : théorème de Varignon etc … ou des propriétés sur les symétries : la composée de trois symétries centrales … etc …
En géométrie euclidienne : le théorème du pivot, reprendre la construction de Gergonne, ou encore illustrer l’existence de la droite d’Euler : les points O, G, H sont alignés.

Vous pouvez enregistrer votre figure avec l’outil d’enregistrement du tableau de bord ci-contre :
Si le fichier est en .txt, (selon le système) mettre .dgp. On peut le relire avec l’appli DGPad ou en ligne en la glissant sur la web-app du même nom.
0 commentaire