Dans les trois modèles plans bornés par un disque (géométrie euclidienne, hyperbolique et elliptique) les droites de la géométrie sont représentées par des arcs de cercle.Or la gestion continue de l’intersection d’arcs de cercle relève d’une problématique fondamentale de la géométrie dynamique : l’incompatiblité entre la continuité et le déterminisme. Cette page donne quelques informations à ce sujet, et présente plusieurs solutions utilisées. Il n’est pas du tout nécessaire de rentrer dans ces détails pour simplement utiliser les figures du site. Mais ces précisions peuvent intéresser quelques lecteurs plus concernés par l’implémentation de la géométrie dynamique.
Commençons par quelques explorations élémentaires sur le détermnisme des figures.
Dessin / Figure : par dessin, on entend une instance d’une figure.
Une figure dynamique est alors un chemin continu sur l’ensemble des dessins géométriques répondant à la même signification (en particulier la même construction)
Déterminisme : c’est la capacité d’une figure à retrouver son instance initiale si les objets initiaux reprennent des positions initiales. Pour une utilisation scolaire, le déterminisme est la condition minimale d’un cahier des charges pour un logiciel de géométrie dynamique. L’autre est celle de la continuité de l’intersection des objets.
Voyons deux exemples de base
Intersection d’une droite et d’un cercle
Ce type d’intersection ne pose aucun problème. Les changements que l’on observe des intersections sont naturelles dans le contexte dynamique. Une droite, qu’elle soit définie par deux points ou non, est toujours orientée. Quand une droite tourne autour d’un point, ses intersections avec d’autres objets peuvent paraître interchangées, mais elle ne le sont pas par rapport à l’orientation interne à la droite.
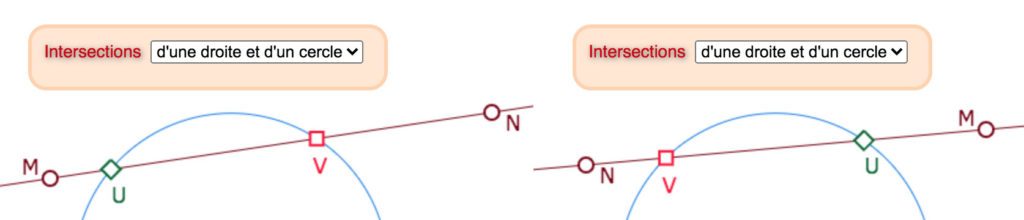
Inversion de U et V quand la droite change d’orientation
De même pour deux cercles, il y a un changement des intersections quand un cercle change d’orientation, par exemple en passant « par l’infini » (selon la construction cela peut être simplement une inversion de deux points). Mais ce changement est lui aussi tout à fait naturel. Par exemple ci-dessous il y a des chemins de modification continue (isotopie) pour passer de la configuration de gauche à celle de droite.
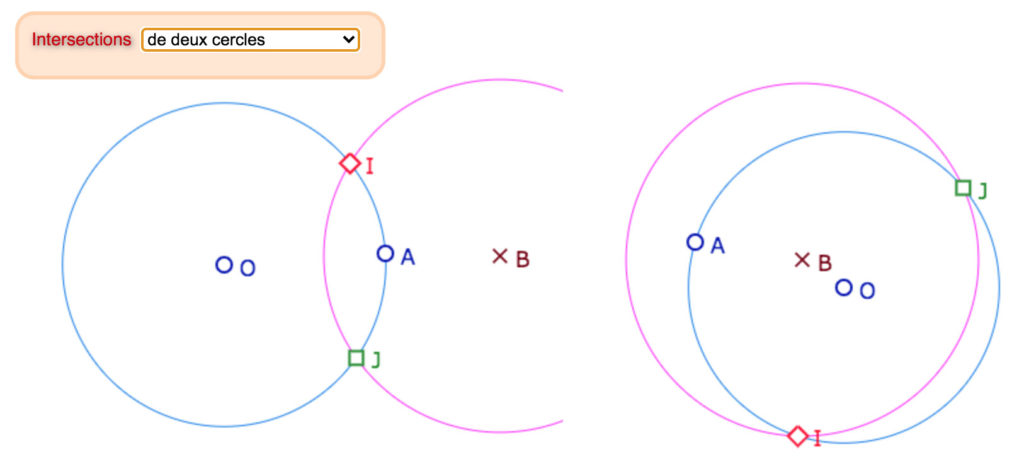
Selon comment on fait aller O vers B, on pourrait croire à un changement d’orientation du cercle et une inversion des intersections, mais si on fait entrer O dans le cercle et qu’on le fait tourner autour de B, on voit que la configuration de droite correspond bien à la continuité des intersections de deux deux cercles
Manipulation de la figure
Dans le cas droite-cercle, placer M ou N à l’intérieur du cercle,
puis faire tourner l’autre point de la droite autour pour voir la continuité des intersections.
Dans le cas des deux cercle, celui de centre B a son rayon modifiable directement en prenant le cercle.
Faire différentes explorations avec le cercle de centre O passant par A comme proposé ci-dessus.
Reste que si la définition proposée d’une figure dynamique était assez claire pour les premiers logiciels de géométrie dynamique (les premières versions de Cabri-géomètre par exemple), elle devient plus confuse avec les logiciels contemporains qui incorporent de la programmation, et en particulier permettent une programmation de rupture, précise et maitrisée, du déterminisme. Il en résulte que le projet d’une conceptualisation axiomatique de la géométrie dynamique, comme nouvelle géométrie, un moment recherchée par certains auteurs a été abandonnée.
Dans l’histoire de la géométrie dynamique, le logiciel Cinderella 1, écrit par Richter-Geber et Kortenkamp à partir de 1999, a eu une place à part. C’est le seul logiciel qui avait été écrit dans un contexte d’étude et de respect total de la continuité, en particulier sur l’intersection des coniques. Les auteurs avaient alors montré – entre autres résultats – que la continuité nécessitait un plongement dans un plan projectif complexe, qui était alors l’environnement naturel du logiciel, utilisé dans l’enseignement supérieur. Finalement, le logiciel a du être entièrement réécrit (Cinderella 2) pour une utilisation scolaire car s’il respectait à merveille la continuité sur des objets forts complexes, il était inutilisable en classe, car ne respectait pas le déterminisme sur des configurations élémentaires.
Nous précisons maintenant quelques éléments théoriques relatifs à cette problématique de continuité et déterminisme, et la mise en œuvre pratique de quelques solutions à ces questions.
Conjecture d’isotopie et théorème de Mnev
Conjecture d’isotopie : l’espace de ces dessins est-il connexe par arc ? Passe-t-on d’une instance à une autre par un chemin continu ? (le déplacement du pointeur du logiciel, souris ou doigt selon l’environnement).
C’est la conjecture d’isotopie que nous allons préciser avec la question de l’orientation.
Conjecture de Ringel (1956) : deux familles de points du plan affine \(\{x_1, x_2, …, x_n\} \) et \(\{y_1, y_2, …, y_n\} \) sont des configurations orientées équivalentes si tous les triplets \(\{x_i, x_j, x_k\} \) et \(\{y_i, y_j, y_k\} \) ont la même orientation.
Pour une figure donnée \(F\), si \(\phi\) et \(\gamma\) sont deux réalisations de \(F\), basées sur les points libres \({A_i}\) et \({B_i}\), existe-t-il un chemin continu de \(A\) vers \(A’\) tel que \(\phi(A’)\) se superpose à \(\gamma(B)\) ?
La conjecture d’isotopie énonce que l’on peut déformer continûment tous les \(x_i\)en les \(y_i\) par une isotopie du plan dans lui-même, de façon que chaque étape intermédiaire toutes les orientations locales soient préservées. Autrement dit l’espace des états d’une configuration orientée de points est un espace topologique connexe.
Théorème de Mnev (1985) – donc avant l’existence de la géométrie dynamique (1988)
La conjecture d’isotopie est infirmée avec une preuve constructible sur un ensemble de 19 points. (rapportée à 14 par Suvorov en 1986).
La conjecture est vraie pour un ensemble de moins de 9 poinrs (Finashin 1986).
Les conséquences pour la géométrie dynamique
Le théorème de Mnev a beaucoup surpris. Pour la géométrie dynamique, il pose la question de la définition même de ce qu’est une figure dynamique en relation à l’accessibilité à toutes ses instances.
Déjà, et c’est fondamental, le théorème de Mnev montre que continuité et déterminisme ne sont pas compatibles.
Une des principales problématiques de la géométrie dynamique va être de garder le déterminisme dans son cahier des charges toute en proposant une continuité maximale, en particulier des intersections.
En pratique, beaucoup de progrès ont été obtenus entre l’origine de la géométrie dynamique (1988) et les outils actuels comme par exemple des progrès substantiels sur la continuité des intersections entre deux coniques – surtout deux ellipses.
Mais, de par des choix de déterminisme incontournables, il reste des problèmes dans des configurations de base que l’utilisateur, si c’est nécessaire, doit résoudre lui-même sur chaque figure. Dans cette page nous présentons deux situations archétypiques que l’on va rencontrer dans les modèles des différentes géométries.
Ces deux situations vont être l’occasion de présenter deux techniques différentes de résolution, selon que la solution est de faire un choix entre deux points :
• qui n’existent pas simultanément
• qui existent simultanément.
1. Continuité de l’intersection de deux arcs de cercle
On l’a dit, nous allons avoir à définir l’intersection de deux droites d’une géométrie (hyperbolique, elliptique ou même non arguésienne dans le modèle de Hilbert) comme intersection de deux arcs de cercles euclidiens dans le modèle proposé pour cette géométrie. Or, la gestion continue de l’intersection d’arcs de cercle demande une intervention spécifique, ceci dans tous les logiciels de géométrie dynamique.
Cela est dû au nécessaire changement d’orientation des cercles définis par trois points quand le centre du cercle passe par l’infini, soit quand, dans la manipulation directe de l’un des trois points, on passe par l’alignement des trois points. Par définition, l’intersection de deux arcs de cercle est l’une des intersections des deux cercles supports. Or quand un arc change d’orientation, cette intersection change. Ci dessous\(U\) et \(V\) sont les deux intersections possibles de deux arcs.
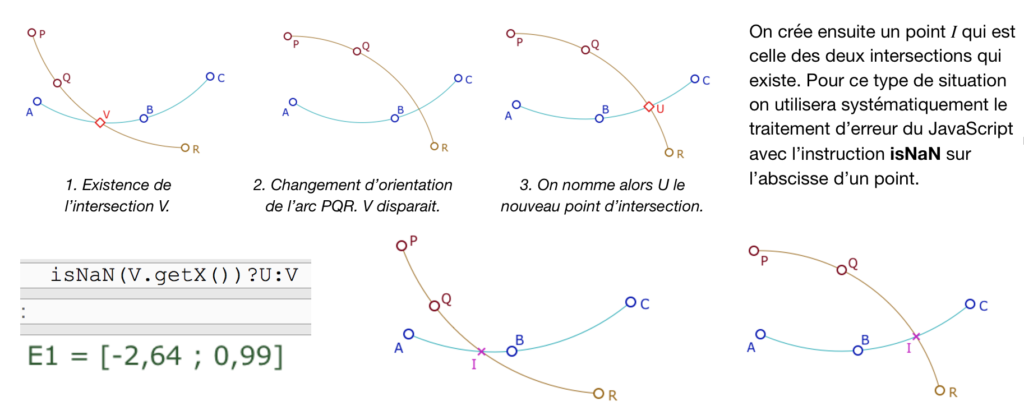
Autrement dit, si \(V\) n’existe pas, on prend \(U\) sinon on prend \(V\). Cette expression renvoie alors les coordonnées d’un point. Point que le logiciel propose, bien entendu, de créer (non illustré ici). C’est le point \(I\) dans les illustrations ci-dessus.
• Explorer la figure en déplaçant l’un des 6 points qui définissant les deux arcs.
• On peut illustrer l’unicité effective du point \(I\) – pour la géométrie dynamique – en créant un segment (par exemple \([CI]\)) et en vérifiant que ce segment existe toujours quand l’un des arcs change d’orientation.
• Rappel : Pour cela il faut d’abord activer le mode standard en cliquant sur le pointeur à gauche dans le tableau de bord. Ensuite cliquer/taper sur le point \(C\) pour faire apparaitre la palette contextualisée. Choisir l’outil segment puis lâcher sur \(I\).
2. Choix entre deux points
Dans un environnement «papier-crayon», ou dans les livres, le choix des intersections est implicite « sur la figure », car cette figure est un dessin statique, mais il doit être nettement plus explicite dans les environnements dynamiques. Voyons le, sur un exemple élémentaire de géométrie euclidienne, la construction du quatrième point d’un parallélogramme par ses seules propriétés métriques : un quadrilatère non croisé dont les côtés opposés sont de même longueur, ce qui est la construction « au compas » souvent proposée aux élèves du collège.
Soient donc trois points \(A, B, C\) non alignés. On se propose de construire \(D\) tel que \(ABCD\) soit un parallélogramme. \(D\) est à l’intersection du cercle de centre \(A\) de rayon\(BC\) et du cercle de centre \(C\) de rayon \(BA\).

Mais laquelle des deux intersections ? Dire que c’est celle «qui réalise le parallélogramme» remet en valeur la géométrie perceptive du début de l’école primaire alors qu’au début du collège on est dans une «géométrie des propriétés».
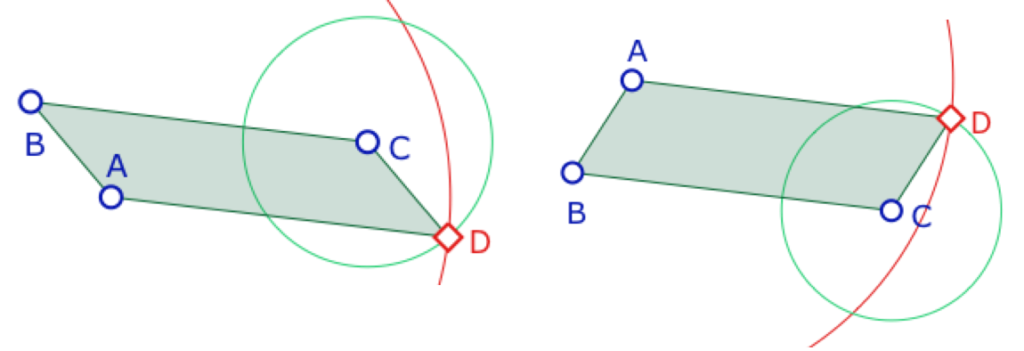
D’un point de vue dynamique, ce n’est pas le point simplement pris dans la figure comme l’illustration de gauche, car cette intersection, dite «prise à la volée» ne correspond pas à la situation de droite.
Il faut donc spécifier, algorithmiquement, laquelle des deux intersections du cercle convient. On peut arriver assez facilement à faire préciser aux élèves qui rencontrent ce problème, par des propriétés de la symétrie centrale, que c’est celle des deux intersections qui est dans l’autre demi-plan de \(B\)par rapport à la droite \((AC)\). Et comme cette droite \((AC)\) est la droite des centres des deux cercles, c’est aussi celle des deux intersections qui est la plus éloignée de \(B\).
On aurait pu reprendre la technique précédente avec un isNaN sur l’intersection des côtés \([AD]\) et \([BC]\). On se propose cette fois de ne pas utiliser le traitement d’erreur du langage, mais plutôt l’existence des deux intersections.
En pratique, on nomme donc les deux intersections \(U\) et\(V\)et on construit le point \(D\) comme combinaison linéaire booléenne de ces deux points. Cette technique de combinaison linéaire booléenne de points sera souvent utilisée dans les deux modèles du menu « Non Arg », dans plusieurs situations. Voyons cela en détail, c’est l’occasion d’illustrer une des utilisations du mode «expression» du logiciel.
Les deux booléens sont \(d(U,B)>d(V,B)\) et \(d(V,B)>d(U,B)\). Si le premier est vrai la solution est le point \(U\) sinon – si le second est vrai – c’est le point \(V\). Dans l’illustration ci-dessous à gauche, prise en cours d’écriture de l’expression, la solution est le point \(V\) donc le produit \(U(d(U,B)>d(V,B))\) est le point \(U\times 0\) soit l’origine du repère, ce que rend l’expression E1. On note l’icone «Point» qui permet de créer le point. L’illustration de droite correspond à l’expression booléenne complète. On créé ainsi le point \(D\) rendu par l’expression E1.

Clairement, le parallélogramme est une figure fondamentalement affine : \(D\) est toujours, tout simplement, le symétrique de \(B\) par rapport au milieu de \(A\) et \(C\), ce qui est sa définition en classe de 5° au collège. En faire une figure euclidienne complique la construction dynamique. La figure suivante propose de manipuler cette configuration avec plusieurs options d’exploration.
Agir sur les trois points de base A, B et C, en choisissant les différentes options proposées dans la figure.