Avec les bissectrices, on aborde une situation plus complexe, à la fois d’un point de vue théorique et d’un point de vue de mise en oeuvre des figures dynamiques.
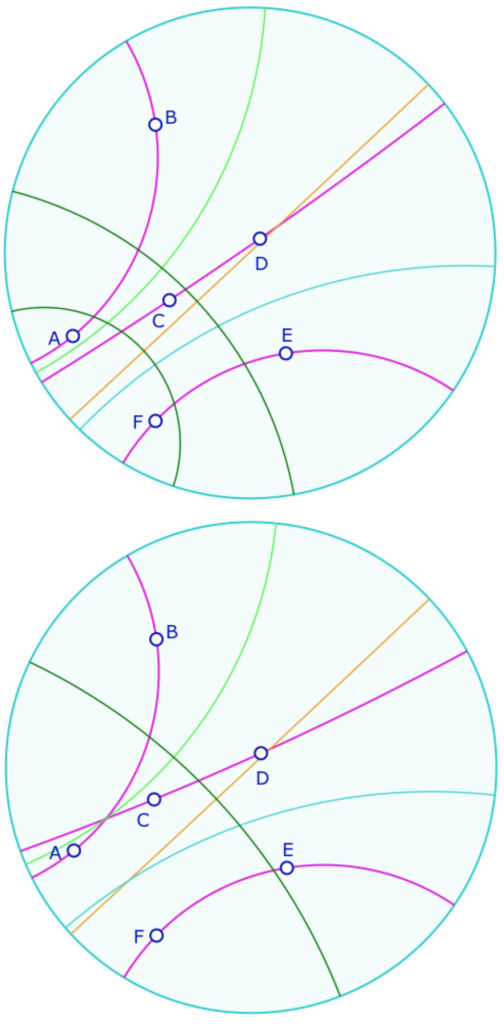
Aspect théorique : les bissectrices d’un trilatère ne sont pas, en général, en pinceau.
Ci-contre, la droite en vert clair est la bissectrice de \((AB)\) et \((CD)\), en bleu celle de \((CD)\) et \((EF)\), et en marron, celle de \((AB)\) et \((EF)\). Or on voit que les perpendiculaires communes, en vert foncé, de deux couples de bissectrices ne sont pas confondues : les bissectrices du trilatère \((AB), (CD), (EF)\) ne sont pas en pinceau.
Aspect pratique : rencontre avec la dualité continuité/déterminisme.
Il n’y a pas de propriété caractéristique des trilatères ayant leurs bissectrices en pinceau. Bachmann montre (Th 21a de cette page) néanmoins que, pour des trilatères sans sommets (pas de sécantes), si deux bissectrices sont sécantes alors les bissectrices des trois droites sont en pinceau. Et c’est un résultat théorique très utile en pratique.
Mais en géométrie dynamique, on s’intéresse aussi à la continuité des solutions. Or on a déjà présenté l’antagonisme qu’il existe entre déterminisme et continuité quand les situations sont un peu complexes. C’est même le cœur du progrès de l’implémentation en géométrie dynamique : maintenir le plus la continuité en respectant toujours le déterminisme.
Les bissectrices sont l’occasion d’illustrer très concrètement cette question. Des solutions seront présentées et utilisées un peu plus loin dans cette page, sans que cela soit nécessaire de détailler les aspects techniques utilisés.
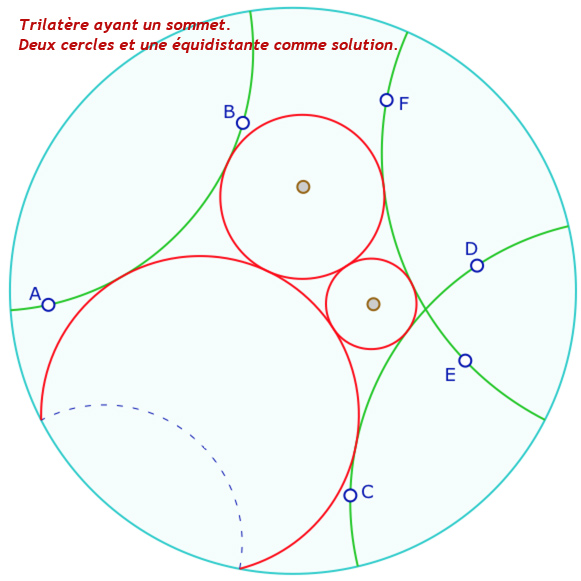
Ci contre, on déplace légèrement \(C\), deux bissectrices sont sécantes mais pas les trois contrairement au théorème que l’on vient de citer, car on a privilégié la continuité de la bissectrice verte : en passant de la situation du haut à celle du bas, il est assez naturel que la bissectrice verte devienne la bissectrice intérieure de l’angle à l’intersection des deux droites \((AB)\) et \((CD)\).
Implémenter un maximum de continuité
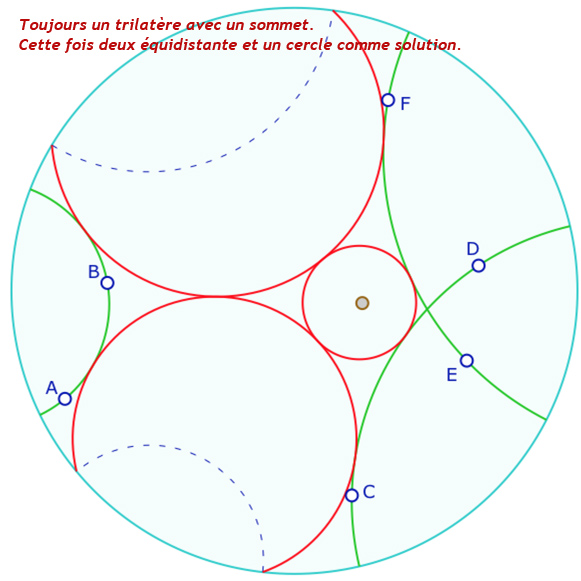
Le théorème de Bachmann n’est bien entendu pas faux : il y a bien des bissectrices en pinceau comme ci- contre : c’est une autre bissectrice que celle utilisée par continuité de la manipulation directe (première illustration à gauche). Dans la seconde illustration de gauche, on a fait tourner \(C\) autour de \(D\), on a donc une autre position des points \(C\) et \(D\) mais la même droite \((CD)\). Cette fois, c’est la bissectrice initiale, celle en vert, qui est en pinceau avec les deux autres.
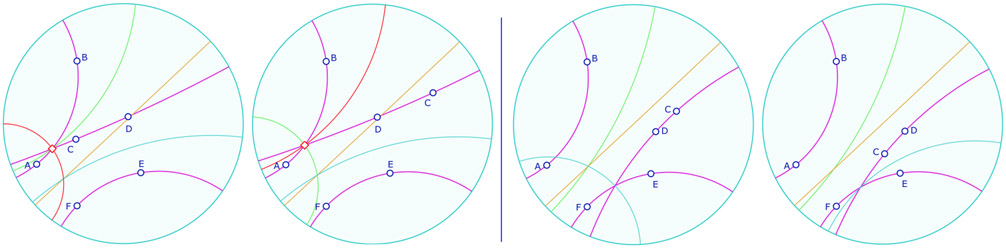
Cet exemple illustre la subtile différence entre théorie et implémentation dynamique pratique. La théorie de Bachmann traite des droites en général. Dans le champ des configurations nous manipulons des droites définies par deux points : ce n’est pas la même chose pour la manipulation, surtout quand les trilatères sont «avec un sommet».
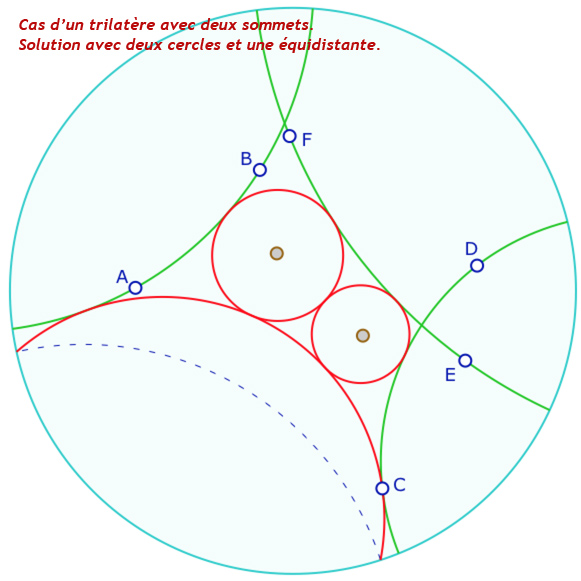
Dans les deux dernières illustrations ci-dessus, on rend cette fois les droites \((CD)\) et \((EF)\) sécantes, on a la même situation : un cas où les bissectrices choisies sont en pinceau, un autre cas (inversion de \(C\) et \(D\)), où il faudrait choisir une autre bissectrice (non présente dans l’illustration).
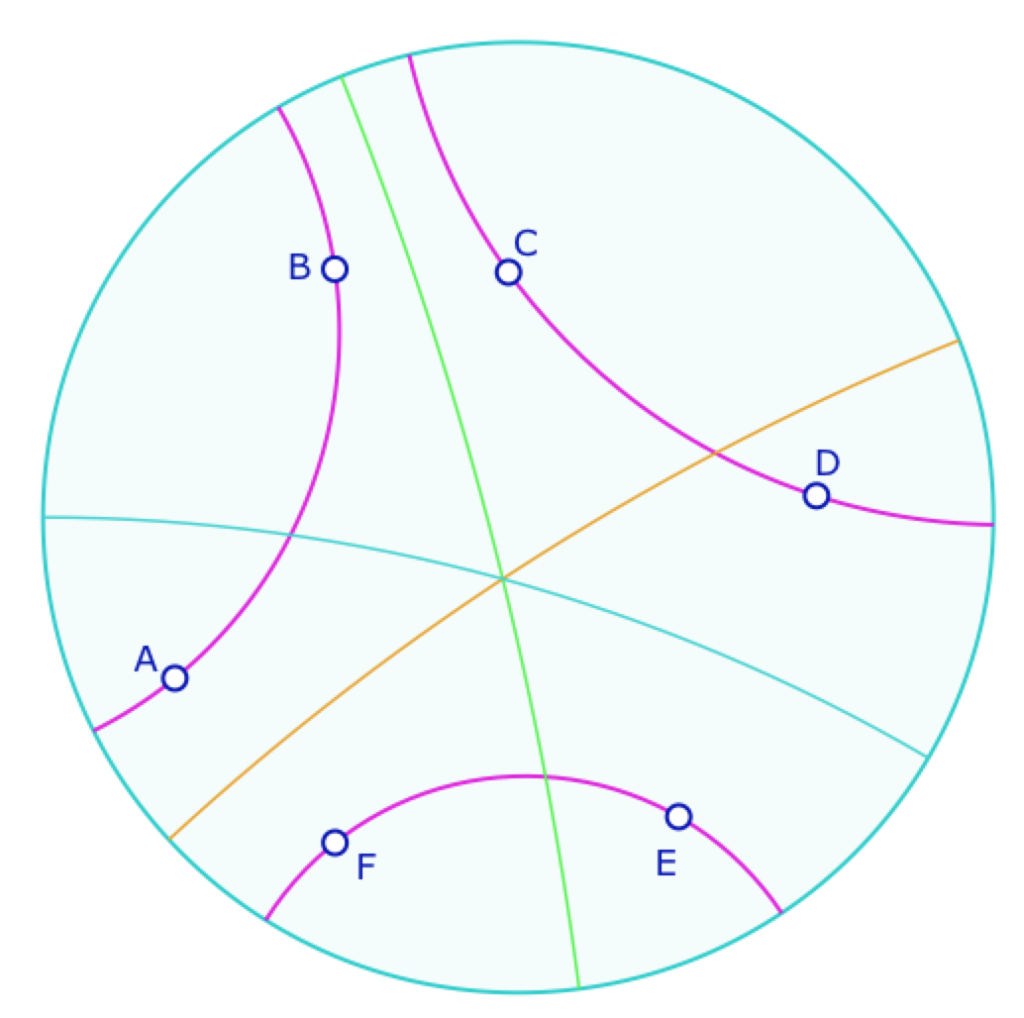
Continuité pour les bissectrices (pour les configurations de Gergonne et de Malfatti)
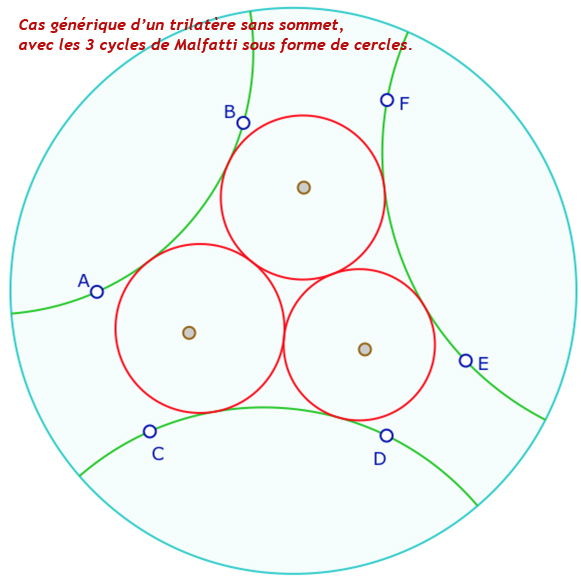
D’une manière générale on traitera des trilatères comme ci-contre (qu’on dira « de Bachmann ») : des trilatères sans sommet, et bissectrices sécantes, donc en faisceaux à centre. La macro mise en œuvre assure la continuité quand les trilatères deviennent « à sommet ».
Toutefois, on aura compris qu’il n’y a aucune chance d’obtenir une continuité totale, en particulier en faisant tourner un point tout autour d’un autre.
Signalons que les macros développées pour ce menu DP mais aussi dans les menus Ell et PS sont, volontairement, entièrement géométriques.
Une autre approche serait possible, avec la programmation Blockly qui permet d’aborder autrement les rapports entre déterminisme et continuité.
Le point de Gergonne
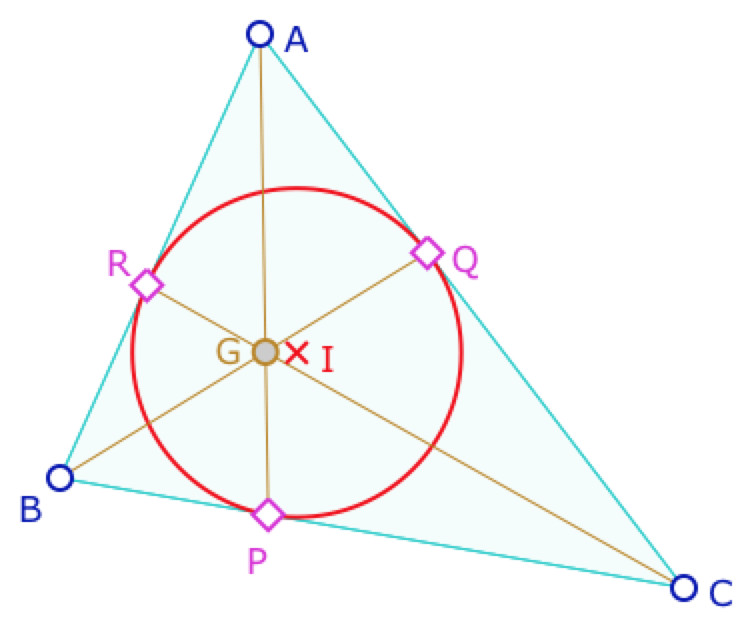
Soit un triangle \(ABC\), \(I\), le centre du cercle inscrit, \(P, Q, R\) les contacts du cercle inscrit sur les côtés du triangle. Alors les trois droites allant d’un sommet au point de contact du côté opposé sont concourantes. Ce point de concours est connu comme étant le point de Gergonne.
Cette propriété, en géométrie euclidienne, se montre facilement avec, par exemple, l’outil barycentrique, ce qui en fait une preuve uniquement euclidienne. On en a donné une illustration dans le modèle borné de l’horisphère.
Pourtant la propriété est absolue, vraie en géométrie hyperbolique, et dans le cas général, pour un trilatère … ayant un cercle inscrit.
En bleu les bissectrices. En mauve les droites d’un faisceau passant par le point de contact du cercle sur la droite opposée.
Manipulation : on peut transformer le trilatère sans sommet en un trilatère ayant un, deux ou trois sommets.
Préférer ouvrir la figure dans un nouvel onglet
Explorations diverses (dont la continuité) sur les bissectrices d’un trilatère.
Les trois bissectrices sont déjà construites ainsi que deux de leurs perpendiculaires communes quand elles ne sont pas sécantes.
Vous pouvez refaire – par exemple – la figure de Gergonne, c’est assez rapide.
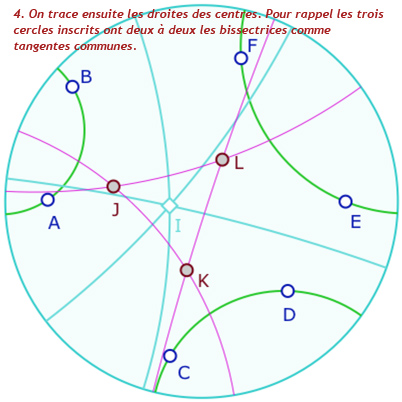
Construction de Malfatti d’un trilatère
Ce travail sur la continuité, basé sur l’implémentation d’une orientation des droites hyperboliques et de leurs bissectrices, permet de réaliser la construction de Malfatti pour des trilatères. On a déjà présenté une lecture « absolue » de la construction euclidienne classique lors des constructions dans le modèle DE (disque euclidien borné).

La seule difficulté est dans la réalisation des bissectrices de bissectrices (des quadrisectrices) qui soient le plus possible continues en manipulation directe quand les faisceaux de deux droites deviennent à centre. Pour cela des macros spécifiques ont été réalisées, un peu techniques : les menus internes ont un peu évolué. Mais il n’est pas utile d’entrer dans ces détails. On a (pourl’intant) laissé l’ancien vocabulaire « faisceau ».
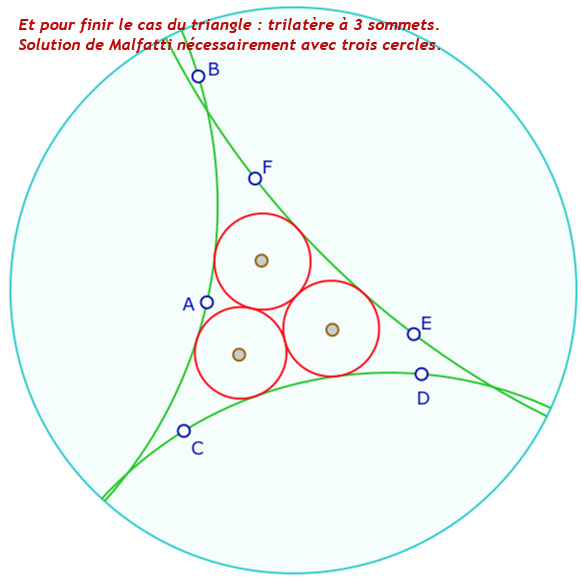
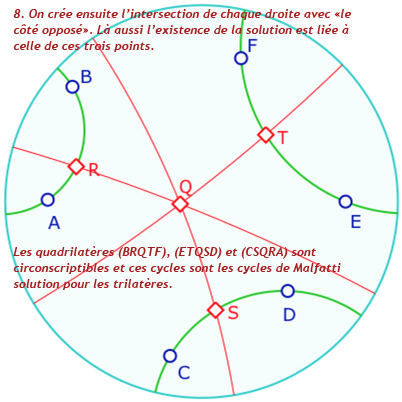
La fin de la construction est proche du cas du triangle puisque l’on construit, justement, des points. Toutefois la solution est plus riche car les cycles peuvent ne pas être des cercles.
Une galerie de quelques configurations de la solution
La construction effective
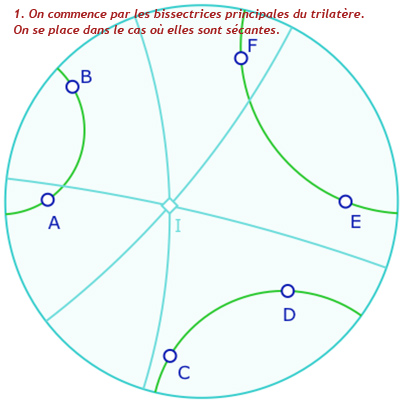
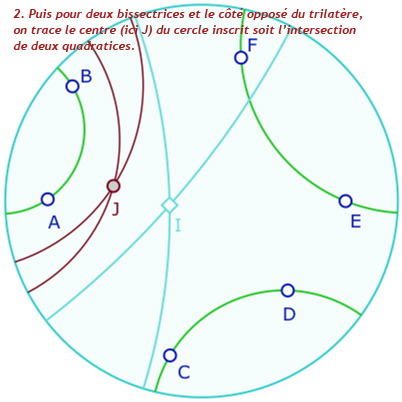
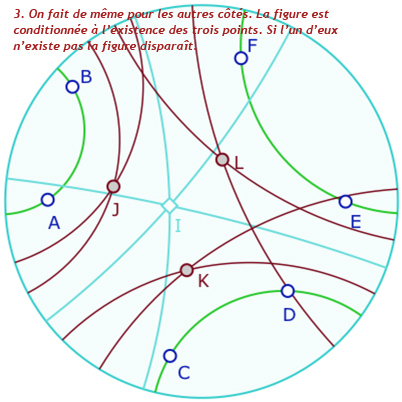
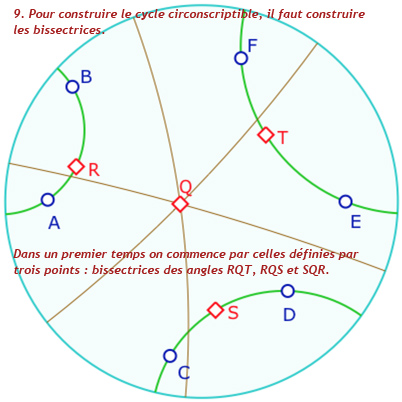
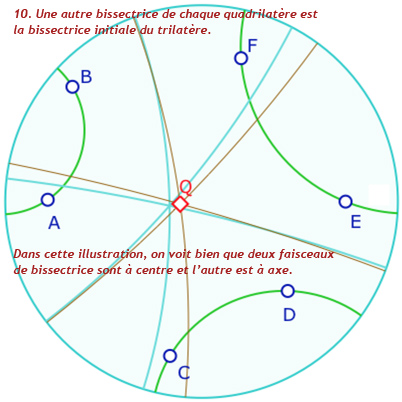
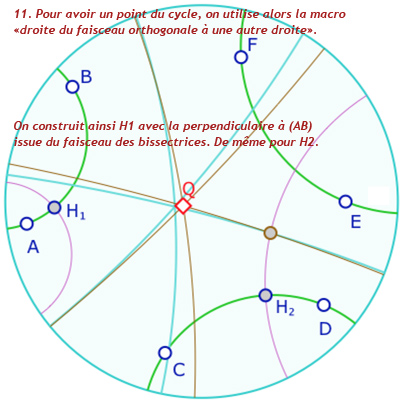
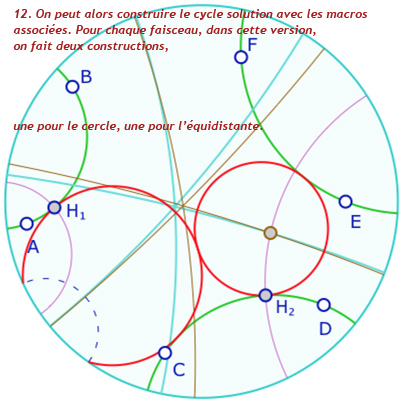
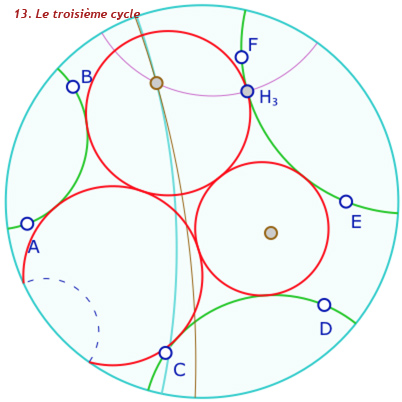
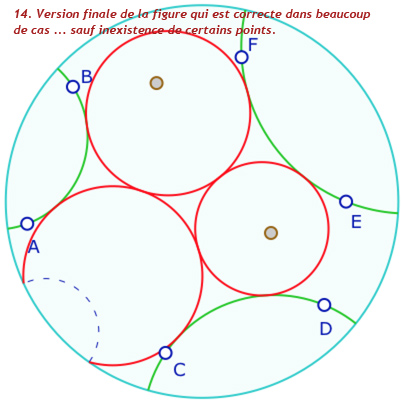
Voici quelques étapes de la construction : en particulier on notera, à l’étape 12, que l’on utilise les deux macros « cercle par centre et point » et «équidistante par axe et point ». pour rendre un cycle. Ce n’est pas trop dans l’esprit de l’objet unique de la géométrie dynamique. C’est donc une étape perfectible. Dans de futurs articles de blog sur Bachmann, on s’autorisera une macro-construction «cycle par pinceau et point ». La galerie ci-dessous est assez technique. Elle est réservé en seconde lecture aux personnes qui se sont déjà questionnées sur ce type de construction.
Présentation de la construction de Malfatti en 13 étapes
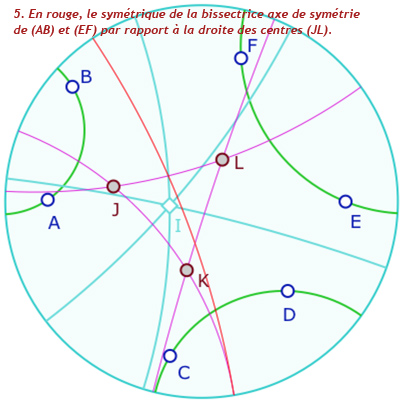
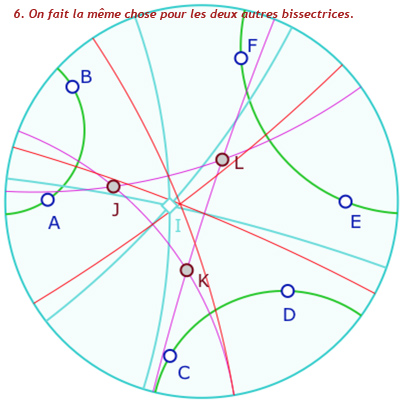
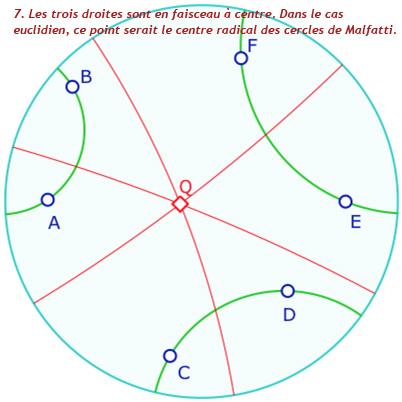
Dans la figure suivante vous pouvez explorer les différentes possibilités de la construction. On propose aux plus téméraires de la compléter avec la «droite de centres» (en mauve ci-dessous) afin de construire le premier point de Ajima-Malfatti, à l’intersection des trois droites issues d’un pinceau de deux côtés et passant par l’intersection des deux cycles opposés, comme ci-dessous.
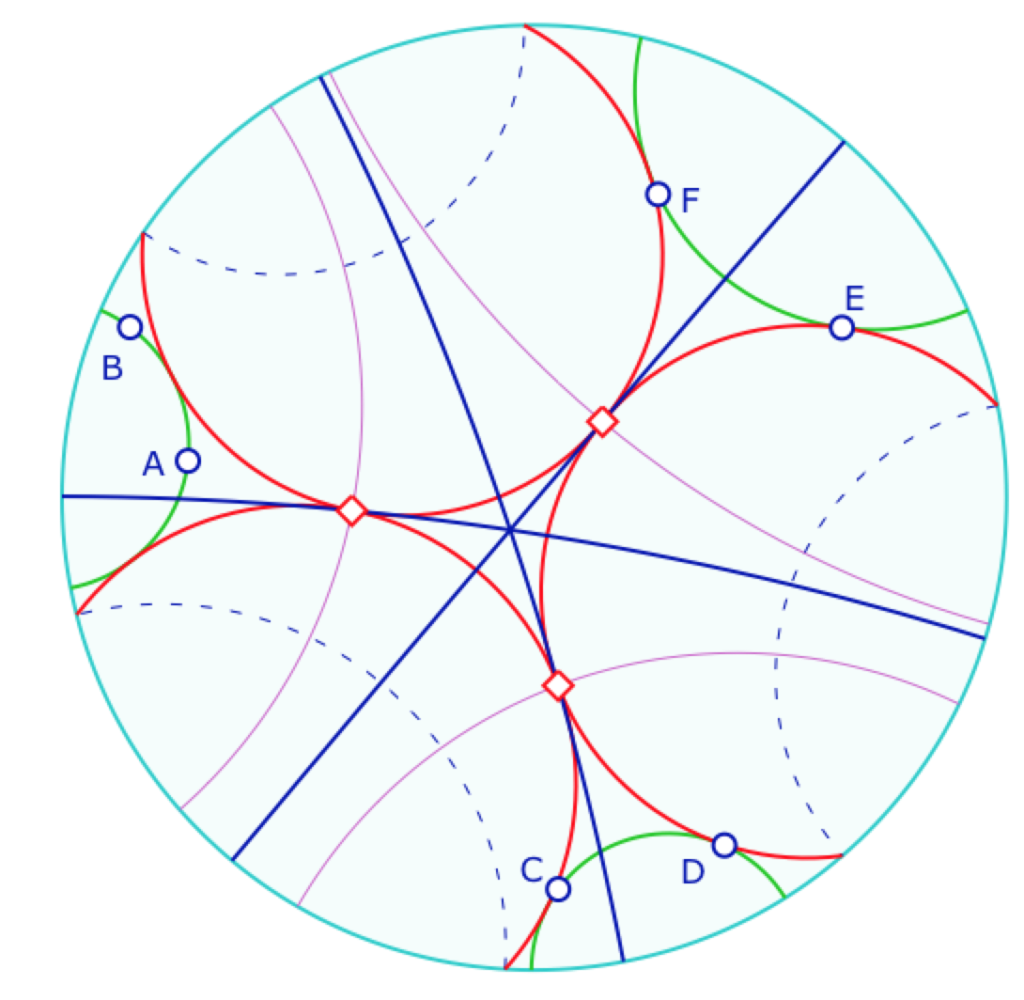
Malfatti d’un trilatère – Manipulation de la figure et compléments de la figure
On utilise les macros du dossier « Faisceaux ». Pour la droite des centres, c’est l’intersection de deux faisceaux.
Pour le point de Malfatti, utiliser la macro « droite du faisceau par un point » .
Ensuite dans le dossier « Technique » utiliser l’intersection de deux droites pour construire le point.
Nouveau dossier de macros personnelles
Une mise à jour optimisée des macros du disque de Poincaré a été effectuée en février 2024 à travers cet article. Utiliser désormais plutôt ces macros pour faire soi-même des figures dans le disque de Poincaré.