Les axiomes 3 et 4 portaient sur la composée de trois droites dans le cas des faisceaux à centre ou à axe. Avant d’aborder les théorèmes fondamentaux sur les pinceaux, dans une première section, on explore le « mélange » de points et de droites. Plus précisément nous allons caractériser quand le produit \(AbC\) est une droite et quand \(aBc\) est un point.
Dans cette page on fait référence systématiquement aux premiers théorèmes développés dans cette page (s’ouvre dans un nouvel onglet).
Illustrations euclidiennes du contexte
Pour illustrer en terrain connu les développements absolus qui vont suivre, on peut commencer par regarder ce qu’il en est d’un point de vue euclidien :
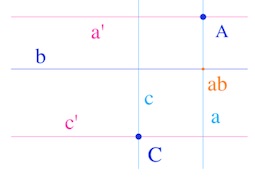
Étant donné deux points \(A\) et \(C\) et une droite \(b\), on peut étudier \(AbC\) en décomposant les points \(A\) et \(C\) en des droites parallèles et orthogonales à \(b\) en \(A=aa’\) et \(C=cc’\).
Alors \(AbC=aa’bc’c\) avec \(a’, b, c’\) parallèles donc en pinceau, le produit de ces trois droites est une droite \(d\) parallèle à \(b\).
Ainsi \(AbC=adc\) avec \(d\) orthogonale à \(a\) et \(c\)
On conclu alors – voir le paragraphe sur la lecture algébrique de l’incidence – que le produit \(AbC\) est une droite ssi le point \(ab\) est sur \(c\) c’est-à-dire \((AC) \perp b\).
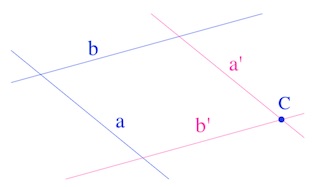
Pour l’étude euclidienne de \(aCb\), puisqu’il n’y a qu’un point en jeu, on peut directement se placer dans le vectorialisé du plan affine, et considérer les droites \(a’\) et \(b’\) parallèles à \(a\) et \(b\) passant par \(C\) : les transformations vectorielles sont les mêmes.
Alors il est clair, avec des notations évidentes, que : \(\overrightarrow{a’} \, \overrightarrow{C} \, \overrightarrow{b’} = -Id \quad\) ssi \( \quad a’ // b’\).
C’est ce que l’on va essayer de transcrire dans un vocabulaire plus général, où il n’y a pas de parallèles – mais des perpendiculaires communes – et pas de vectorialisé car pas de translations.
Deux théorèmes préliminaires
Th 10 : une lecture algébrique du théorème de Hjelmslev
En pratique, sauf cas particuliers, \(AbC\) est une droite ssi, \((AC)\) est orthogonale à \(b\).
Illustration dynamique dans le contexte hyperbolique
On illustre le fait que \(AbC\) est une droite en prenant la médiatrice d’un point \(M\) et de \(M^{AbC}\) : c’est la droite rouge. \(AbC\) est effectivement une droite si cette droite rouge est indépendante du point \(M\).
Dans cette figure, agir sur le point \(b_2\) (aimanté par la droite grise en pointillé) pour que la droite \(b = (b_1b_2)\) soit perpendiculaire à \((AC)=v\).
On a aussi construit les droites \(a\) et \(c\) de la preuve suivante.
Preuve
Si \(A=C\), \(AbA\) est une droite par conjugaison, et il existe toujours \(v \mid A,b\): il suffit de choisir la (une) perpendiculaire à \(b\) incidente à \(A\). Le théorème est trivial dans ce cas ; on peut désormais supposer \(A \neq C\).
Si \(A\) et \(A\) sont deux points distincts, le cas particulier ci-dessus donne une indication : considérons la droite \(v\) incidente à \(A\) et \(C\) : par l’axiome 1, cette droite existe, et on a \(v \mid A, C\).
Notons alors \(c=Cv=vC\) (la droite orthogonale à \(v\) passant par \(C\)) et \(a=Av=vA\) la droite orthogonale à \(v\) passant par \(A\). On a aussi \(A=av=va\). On peut alors écrire : \(AbC=vabcv\). Remarquons que les droites \(a\) et \(c\) sont distinctes car \(A\) et \(C\) sont distincts.
Première implication : si \(v \mid b\) comme on a aussi \(a \mid v\) et \(c \mid v\), par l’axiome A3, \(a, b, c\) sont en pinceau, il existe une droite \(d\) tel que \(abc=d\), et par le complément de l’axiome A3 (Th. 6), de plus \(d \mid v\), c’est-à-dire \(vdv=d\). Autrement dit \(AbC=d\) soit \(AbC\) est une droite.
Réciproquement: si \(AbC\) est une droite, par conjugaison, \(vAbCv\) aussi et donc \(v(abcv)v\) est une droite, soit \(abc\) est une droite. On a vu qu’être en pinceau est indépendant de l’ordre des droites et donc \(acb\) est aussi une droite. Or \(a \mid v\) et \(c \mid v\) avec \(a\) différent de \(c\). Par le théorème 9, réciproque de l’axiome A4, il vient \(b \mid v\).
Complément au Th 10 :
Dans le cas où \(AbC\) est une droite \(d\), et \(v\) une droite telle que \(v \mid A, b, C\) alors \(d \mid v\).
Preuve du complément
Dans le cas où \(A\) et \(C\) sont distincts, le complément de l’axiome A4 appliqué à ce qui est ci-dessus suffit à assurer que \(d \mid v\).
Dans le cas où \(A=C\), la droite \(d\) est \(AbA\). Or si \(v \mid b, A\), alors \(AbA \mid AvA\) par conservation de la relation \(\mid\) par isométrie. Or \(AvA=A\) donc \(d \mid v\).
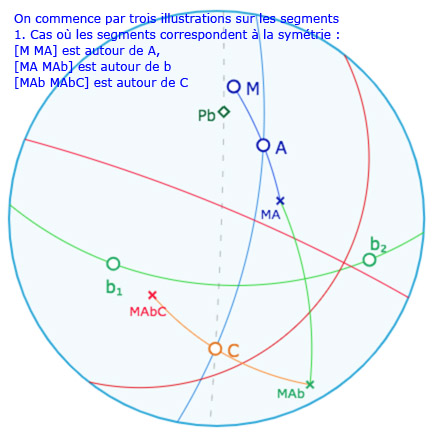
Illustration du théorème dans le contexte elliptique
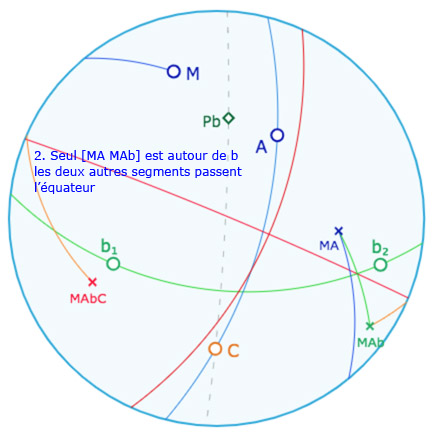
On a toujours un point \(M\), son symétrique \(M^A\)par rapport à \(A\), noté \(MA\) dans la figure suivante, le symétrique \(M^{Ab}\) de ce point par rapport à la droite \(b=(b_1b_2)\), noté \(MAb\) dans la figure, et enfin son symétrique par rapport au point \(C\), soit \(M^{AbC}\), noté \(MAbC\) dans les illustrations. Dans le contexte elliptique le médiateur entre \(M\) et \(M^{AbC}\) est la réunion de deux droites orthogonales : ce sont les droites rouges. \(AbC\) est effectivement une droite si une de ces deux droites rouges est indépendante du point \(M\). C’est le cas quand \(A\) est sur la perpendiculaire à \(b\) passant par \(C\) (droite grise en pointillé, qui aimante \(A\)).
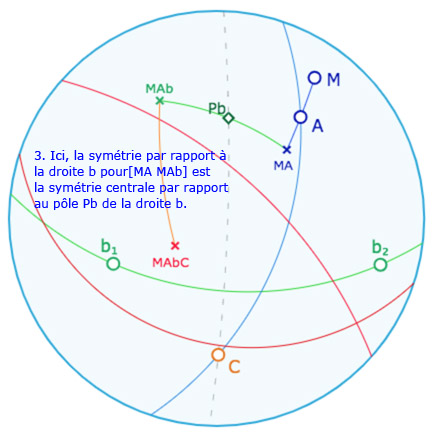
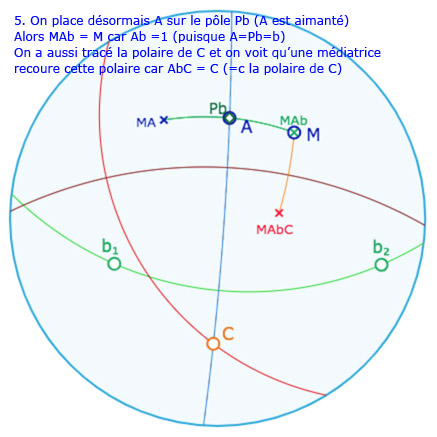
Le contexte elliptique est plus riche car le point \(A\) peut aussi être sur le pôle \(P_b\) de la droite \(b\). Voici une galerie de 6 illustrations de ce que l’on peut expérimenter avec la figure suivante.
Galerie de 6 illustrations de la figure suivante
La figure dynamique associée
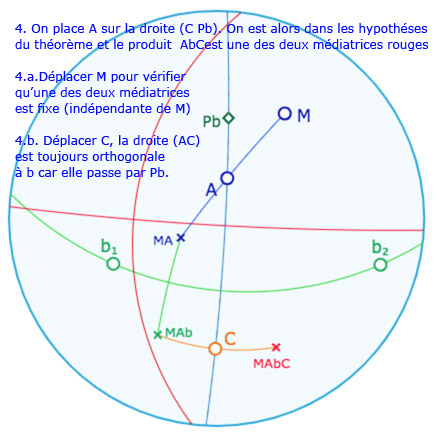
Agir sur les points \(M, A, C\) ou les poignées \(b_1, b_2\) pour explorer les situations proposées ci-dessus … ou d’autres …
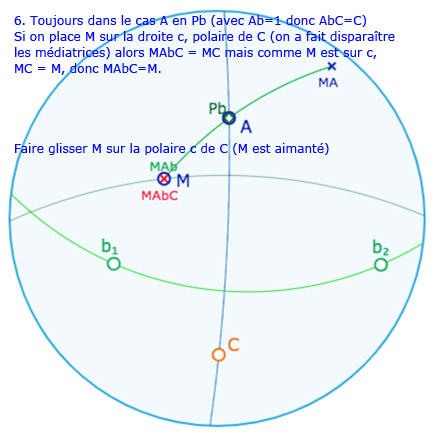
Placer ensuite \(A\) sur la droite \((C P_b)\) et alors \(M\) sur la polaire de \(C\).
Th 11 : théorème dual du précédent
\(aBc \; \mathrm{e}st \; \mathrm{un} \; \mathrm{point} \; \quad \mathrm{ssi} \quad \exists v \; \mathrm{telle} \; \mathrm{que} \; v \mid a,B,c\)En pratique, sauf cas particuliers, \(aBc\) est un point ssi, \(B\) est sur la perpendiculaire commune à \(a\) et à \(c\).
Ce théorème se montre simplement en revenant au précédent par conjugaison.
Sens direct : si \(aBc\) est un point \(D\) alors \(BcD=a\) est une droite et par le complément ci-dessus au théorème 10, il existe une droite \(v\) telle que \(v \mid B, c, D, a\).
Sens réciproque : Supposons qu’il existe une droite \(v\) telle que \(v \mid a, B, c\).
Notons \(b=Bv\). Par hypothèse \(vc=cv\). Puisque l’on a \(v \mid a, b, c\), par l’axiome A4, \(abc\) est une droite \(d\) telle que \(d \mid v\) (complément à l’axiome A4).
On peut alors écrire \(aBc = abvc = abcv = dv\) qui est un point puisque \(d \mid v\). Ainsi \(aBc\) est un point \(D\) et de plus \(D \mid v\).
Figure d’illustration dans le cadre hyperbolique
Avec les notations identiques à la figure précédente, on peut proposer cette illustration
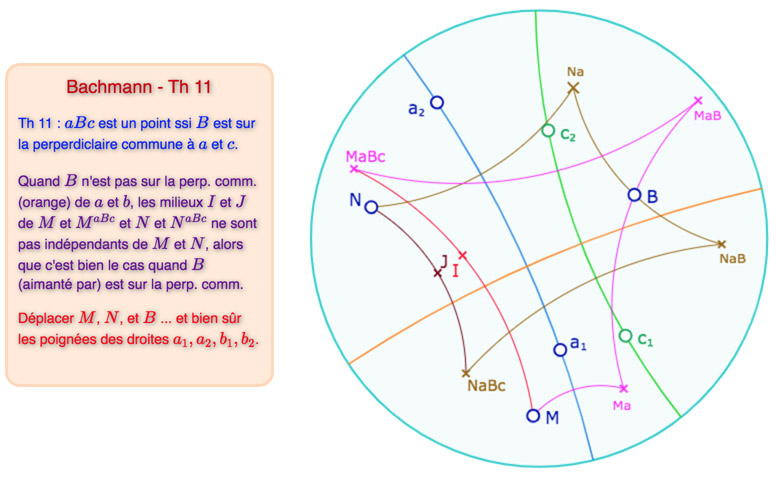
Ci-dessus le cas général de la figure, ci-dessous le cas du théorème, avec \(B\) sur la perpendiculaire commune à \(a\) et \(c\) : \(I\) et \(J\) sont confondus.
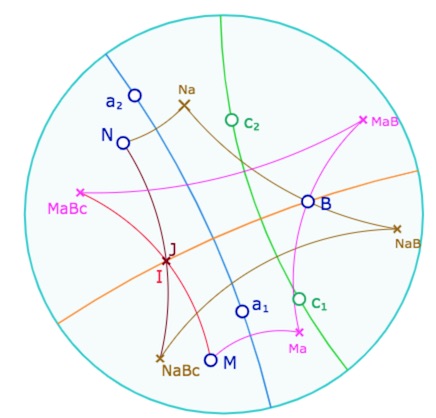
Lancer cette figure dans un nouvel onglet.
Complément au Th. 11 :
Dans le cas où \(aBc\) est un point \(D\), et \(v\) une droite telle que \(a, B, c \mid v\), alors \(D \mid v\). Preuve : ceci résulte de la preuve ci-dessus (du sens direct).
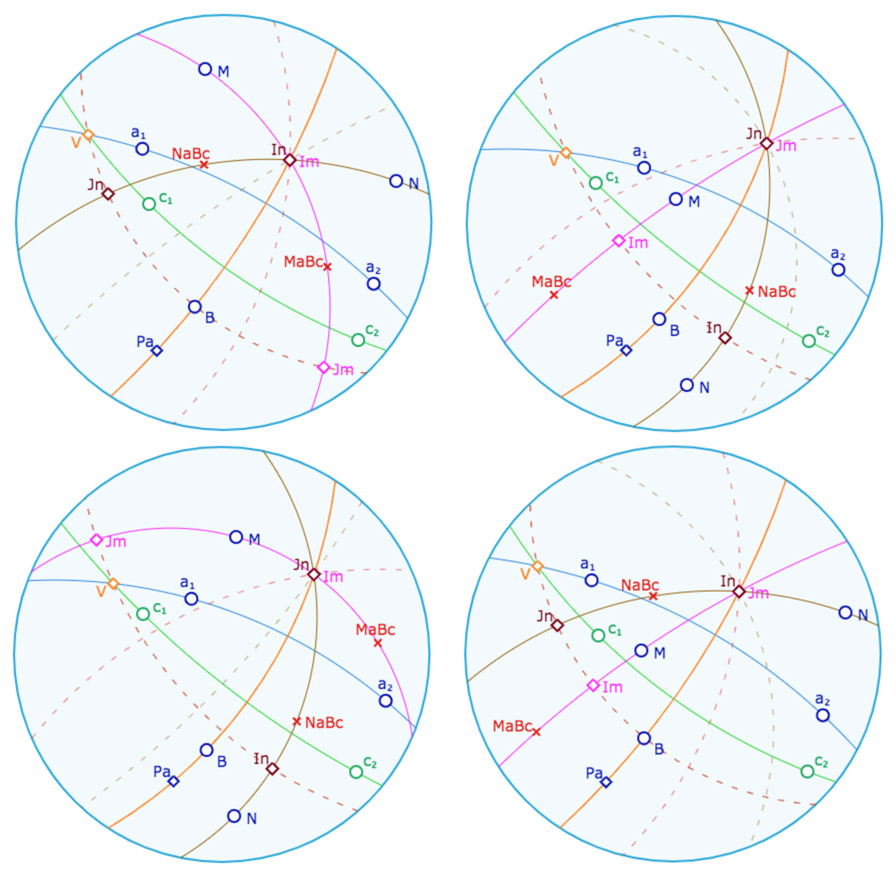
Illustration elliptique de ce théorème
La situation est bien plus riche car deux points ont deux milieux et deux médiatrices. Voici quelques illustrations.
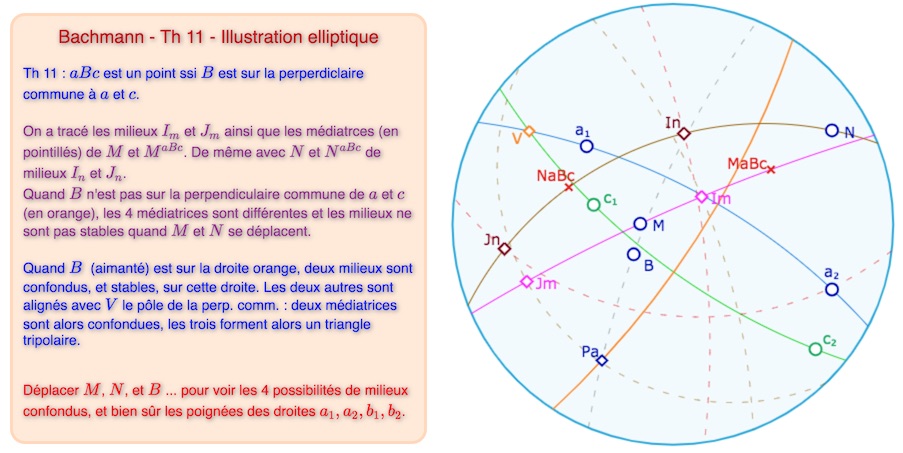
Ci-dessus, présentation générale, ci dessous, les 4 possibilités de concordance des milieux d’indices \(m\) ou \(n\),
respectivement, en haut \(I_m=I_n, \; J_n=J_m\) et en dessous \(J_n=i_m\) et \(I_n=J_m\).
Quand \(B\) est sur la perpendiculaire commune, le point \(D\), centre de symétrie, étant un des milieux des segments, la droite qui passe par les deux autres milieux est la polaire de ce point. Par ailleurs, le centre de symétrie – d’après le complément au théorème – étant sur la droite \(v\), polaire de \(V\), sa polaire passe par \(V\) : donc les deux médiatrices communes à \([NN^{aBc}]\) et \([MM^{aBc}]\) sont celles incidentes à \(V\). Ou encore le centre de symétrie cherché est l’intersection des deux médiatrices non incidentes à \(V\).
Lancer la figure associée dans un nouvel onglet
Le théorème de Hjelmslev
« Théorème fondamental des plans métriques »
Bachmann utilise plusieurs fois l’expression « Théorème fondamental des plans métriques» à propos du théorème de Hjelmslev, alors que, dans le contexte où nous le rencontrons, c’est un théorème relativement technique (quasiment un lemme), assez élémentaire. Si on s’interroge sur cet aspect « fondamental » on peut envisager plusieurs points de vue . Sous un angle formel, ce théorème est la première caractérisation de droites en pinceaux de l’axiomatique de Bachmann ; nous verrons plus loin qu’il est ensuite à l’origine de la mise en place d’autres théorèmes fondamentaux sur la transitivité des pinceaux. D’un point de vue technique – en particulier de construction – c’est un théorème essentiel pour la réalisation de figures indépendamment du type de pinceau rencontré ; on comprendra que pour ce site il est fondamental, en particulier pour cela. D’un point de vue épistémologique, ce qualificatif est peut-être aussi un hommage de Bachmann à son illustre prédécesseur, qui a été le premier à travailler sur la possibilité de mettre en évidence une présentation de la géométrie à partir des symétries orthogonales et de leurs compositions.
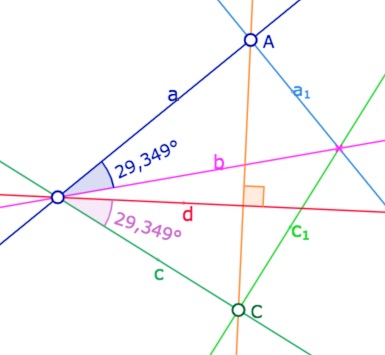
Th. 12 : Hjelmslev – version géométrique du th 10
Soient \(a, a_1, b, c, c_1\) cinq droites telles que \(aa_1=A, \; cc_1=C\), avec \(A\) et \(C\) distincts et telles que \(abc\) soit une droite \(d\).
Alors \(a_1bc_1\) est une droite si et seulement si \(d \mid (AC)\).
Preuve
\(a_1bc_1= a_1(aa)b(cc)c_1= AabcC=AdC\). Par le théorème 10, \(a_1bc_1\) est une droite si et seulement si il existe une droite \(v \mid A, d, C\) soit ssi \(d \mid (AC)\).
ci-contre illustration euclidienne : si \(abc=d\), c’est que \(ab=dc\), d’où l’égalité d’angles.
Illustration hyperbolique
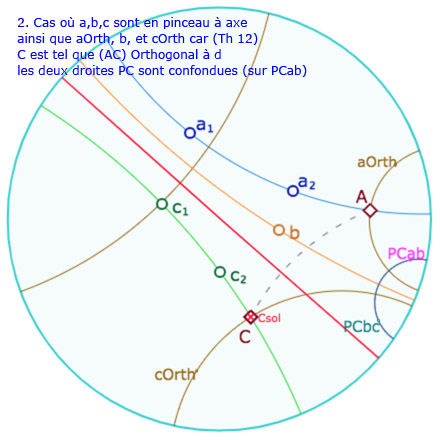
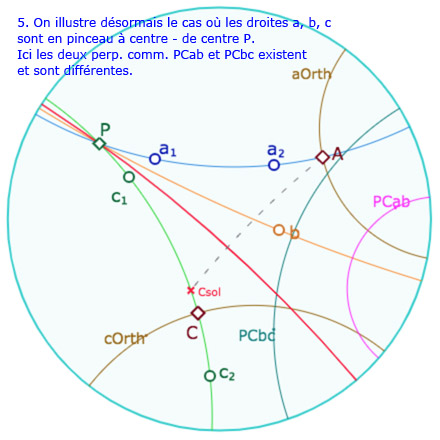
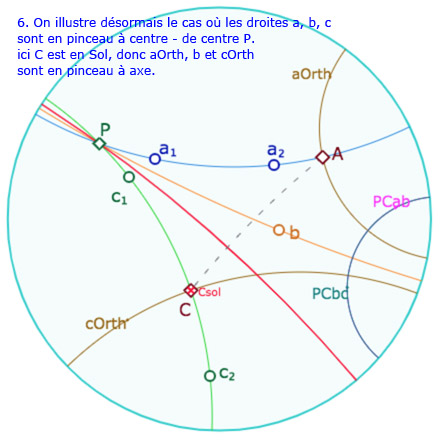
C’est le contexte le plus riche car les pinceaux peuvent être de plusieurs type alors qu’il n’y a qu’un seul type dans le contexte elliptique. Dans la figure suivante, on considère trois droites \(a, b , c\) en pinceau (à centre ou à axe) – dont la question de la construction sera abordée plus loin – on note \(aOrth\) et \(cOrth\) les droites \(a_1\) et \(c_1\) du théorème. Voici une galerie de 8 illustrations de ce que l’on peut faire de la figure suivante.
Galerie de 8 illustrations de la figure suivante
La figure dynamique
Agir sur les poignées \(a_1, a_2, c_1, c_2\) des droites \(a\) et \(b\), mais aussi sur la poignée \(b\) de la droite du même nom,
ainsi que sur les points \(A\) et \(C\) pour reproduire les 8 situations présentées ci-dessus.
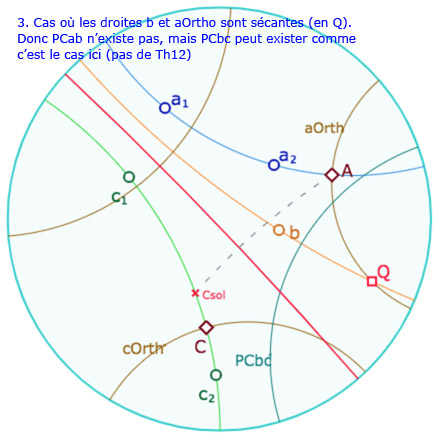
Cas des pinceaux sans support
Mais on sait aussi que, dans le cas hyperbolique, il existe un troisième type de pinceau – pas encore abordé jusque là dans l’axiomatique de Bachmann telle qu’elle est déroulée, mais bien entendu le théorème 12 ayant comme principale argumentation, la situation où le produit de trois droites est une droite, le résultat s’applique aussi dans le cas des « pinceaux sans support » c’est-à-dire quand le pinceau \(\mathscr{P}_{ac}\) est composé de droites parallèles. En voici une illustration :
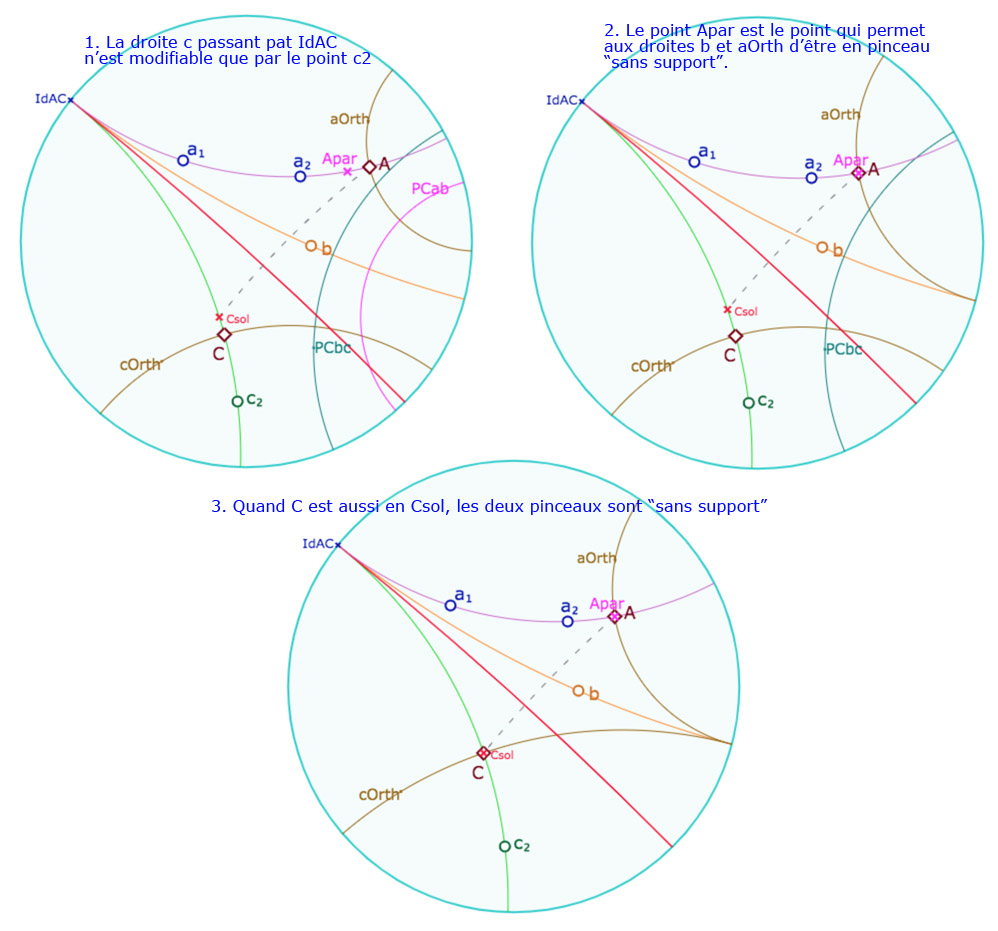
Lancer la figure associée dans un nouvel onglet.
La construction de la droite \(b\) telle que \(a, b, c\) soient en pinceau
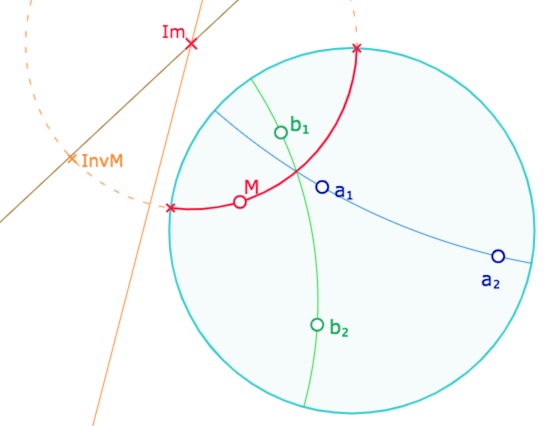
Une première conséquence du théorème de Hjelmlev est la construction de cette droite \(b\) depuis un point \(M\) donné, et ceci, indépendamment du modèle dans lequel on travaille, mais pour l’illustration « séquentielle » on peut avoir envie d’une construction indépendante du théorème lui-même. Voici par exemple une de construction réalisable dans le modèle du disque de Poincaré, à partir des propriétés de l’inversion.
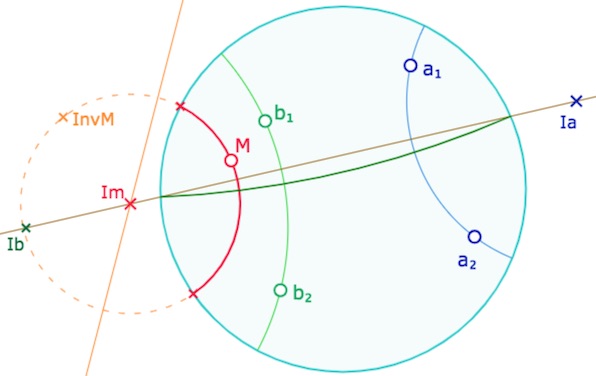
La droite du pinceau \(P_{ab}\) passant par \(M\) est définie par deux contraintes :
• C’est une droite hyperbolique donc la trace d’un cercle passant par \(M\) et son inverse \(Inv_M\) par rapport au cercle horizon, soit de centre un point de la médiatrice euclidienne de \(M\) et \(Inv_M\).
• Comme droite d’un pinceau, son centre euclidien \(I_m\) est sur la droite des centres euclidiens \((I_aI_b)\), et donc à l’intersection de ces deux droites.
Autre illustration : pinceau de droites sécantes
Une première application du théorème de Hjelmlsev
Th 13 : existence d’une droite d’un pinceau donné incidente à un point donné
Soient \(a\) et \(c\) deux droites et \(M\) un point. Alors il existe une droite du pinceau \(\mathscr{P}_{ac}\) incidente à \(M\).

Construction de la droite de \(P_{ac}\) passant par \(M\).
Depuis le point \(M\), on mène les perpendiculaires \(a_1\) et \(c_1\) aux droites \(a\) et \(c\). On note \(A=aa_1\) et \(C=cc_1\) les pieds de ces perpendiculaires.
Si \(A=C\), alors \(A=C=M\) , le pinceau est à centre et la droite \(c_1\) ou la droite \(a_1\) sont une droite solution.
Si \(A \neq C\), soit alors \(d\) la – une(*) – perpendiculaire à \((AC)\) issue de \(M\) (droite orange ci-dessus). Alors la droite (bleue ci-dessus) \(b=c_1da_1\) est une droite passant par \(M\) telle que \(d=a_1bc_1\).
Alors, d’après le théorème de Hjelmslev, \(b\) est la droite cherchée car \(abc\) est une droite.
!*) On a vu dans les premiers théorèmes que le seul cas où il n’y a pas unicité est quand \(M\) est pôle de \((AC)\). Mais dans le cas elliptique, la construction est triviale car il n’y a que des pinceaux à centre.
Lancer la figure de cette illustration dans un nouvel onglet
L’existence, en général, d’une droite incidente à un point donné appartenant à un faisceau donné va être un argument significatif dans les premiers théorèmes sur les faisceaux d’un triangle ou d’un trilatère. Par exemple nous allons voir que sans l’existence d’un point, ne pouvant introduire de cette façon une droite dans un faisceau, nous ne pourrons pas assurer l’existence de certains faisceaux qui existent dès qu’un point existe. Ce n’est bien entendu pas la limite d’une démarche constructive : nous verrons un exemple de non-existence de ces faisceaux, même dans les géométries aussi riches que la géométrie hyperbolique réelle.
Transitivité de la relation « être en pinceau »
et ses conséquences
Avant d’aborder – dans la page suivante – les théorèmes usuels sur les triangles et les trilatères, afin d’obtenir directement que certaines droites remarquables sont en pinceau, c’est le moment d’aller plus loin dans l’étude générale de ces pinceaux. En définissant la relation « être en pinceau », nous avons tout de suite vu qu’elle était réflexive et symétrique. Voyons maintenant :
Th 14 : théorème de transitivité
Si \(a \neq b\) et si \(abc\) et \(abu\) sont des droites, alors \(acu\) est aussi une droite.
Commentaire sur ce résultat : tout d’abord, on peut remarquer que si le pinceau de droites \(\mathscr{P}_{ab}\) est à centre ou à axe, par application des axiomes A3 et A4 de leurs réciproques, le théorème de transitivité est immédiat. En effet, si \(a\) et \(b\) ont un point \(P\) en commun (ce serait la même chose si c’était une perpendiculaire \(g\)) alors \(abc\) étant une droite, \(c\) est incident à \(P\), \(abu\) étant une droite \(u\) est incident à \(P\), donc \(a, c, u\) étant incident à \(P\), \(acu\) est une droite.
C’est en particulier le cas dans les cas euclidien ou elliptique où il n’y a pas d’alternative aux axiomes A3 et A4. Le seul intérêt de ce théorème – et aussi une des forces de cette axiomatique – est sa preuve dans le cas général, en particulier indépendamment du type pinceau, même s’il est « sans support ». Comme c’est le seul cas désormais significatif, nous l’illustrerons dans ce cas ; en pratique dans le cas où\(P_{ab}\) est un pinceau de deux droites parallèles dans le cas hyperbolique.
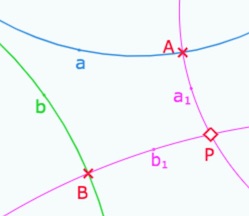
Lemme: les pieds des perpendiculaires à deux droites distinctes issues d’un point n’appartenant à aucune des deux droites sont distincts.
Preuve du lemme : on considère donc \(a \neq b\) et \(P\) non incident à aucune de ces droites. Soient \(a_1\) et \(b_1\) des perpendiculaires à \(a\) et \(b\) incidentes à \(P\) : \(P \, \mathfrak{I} \, a_1,b_1\) , avec \(A=aa_1\) et \(B=bb_1\).
On rappelle que l’incidence \(\mathfrak{I}\) contient, en plus de la relation \(\mid\), les conditions \(Pa_1 \neq 1\) et \(Pb_1 \neq 1\) .
Supposons (par l’absurde) que \(A=B\). On a donc d’une part \(P, A \, \mathfrak{I} \, a_1,b_1\) et en même temps \(aa_1=bb_1\)’, soit encore \(a_1b_1=ab\). Comme \(a \neq b\) on a \(ab \neq 1\) donc \(a_1b_1 \neq 1\) soit \(a_1 \neq b_1\). De \(P, A \, \mathfrak{I} \, a_1,b_1\), on a en particulier \(P, A \mid a_1,b_1\). Par l’axiome A2, on a donc \(P=A=B\), soit \(P \mid a,b\) ce qui n’est pas par hypothèse.
Pour montrer le théorème, Bachmann distingue deux cas. Tout d’abord le cas où il existe un triangle tripolaire. Nous avons vu, avec le théorème 2, que c’est équivalent à l’existence de trois droites \(a, b, c\) de produit \(abc=1\), ou encore à l’existence d’un point \(C\) tel que \(C=c\). Nous montrerons ultérieurement, indépendamment de ce que nous étudions ici, que dans ce cas, nécessairement toutes les droites en pinceau sont en pinceau à centre, et la transitivité a alors été traitée ci-dessus (elle est contenue dans les axiomes). Examinons donc le seul cas qui nécessite une preuve spécifique, celui où un produit de trois droites n’est jamais égal à un, ou encore un point n’est jamais égal à une droite. Nous avons vu (théorème 4) que dans ce cas, un point et une droite étant donnés, il existe une – et une seule – droite incidente à ce point perpendiculaire à cette droite. C’est cette unicité que nous allons appliquer plusieurs fois.
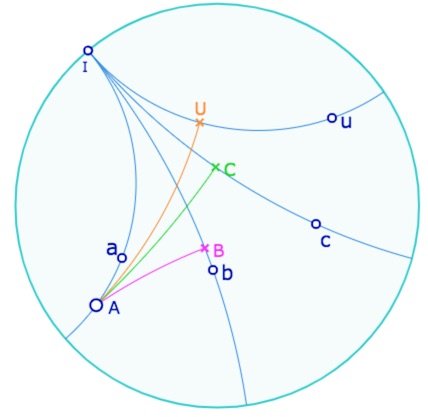
Preuve du théorème : on suppose que les 4 droites \(a, b, c, u\) sont distinctes sinon le théorème est trivial. Soit alors \(A\) un point incident à \(a\) et non incident à \(b\). Alors \(A\) n’est incident ni à \(c\) ni à \(u\) (par le théorème 8, réciproque de l’axiome A3).
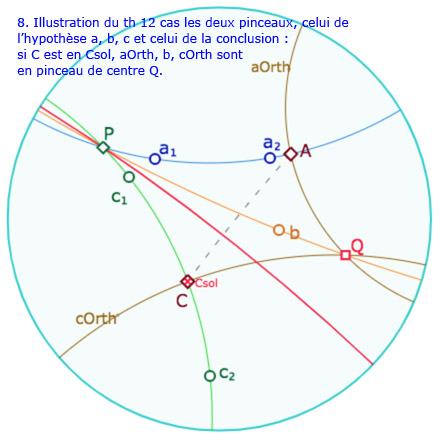
Ci-contre les droites \(a, b, c, u\) sont pilotées par un point du même nom et sont, par trois en pinceau. Bien entendu, les 4 droites sont déjà en pinceau : il n’y a pas d’alternative puisque c’est justement ce que l’on va montrer.
On considère les perpendiculaires \(b_1, c_1, u_1\), respectivement à \(b, c, u\) passant par \(A\). D’après le lemme précédent, les pieds des perpendiculaires \(B, C, U\) sont distincts.
Par hypothèse – parce que la nature d’être une droite est indépendant de l’ordre des produits – on a que \(bac\) et \(bau\) sont deux droites. On est donc dans des configurations du théorème de Hjelmslev avec des pinceaux à centre, de centre \(A\). Ainsi par deux premières application du théorème on peut écrire les relations
(*1) \(\quad b_1ac_1 \perp (BC)\) et \(b_1au_1 \perp (BU)\).
Deux cas sont alors possibles : soit les trois points \(B, C, U\) sont alignés soit ils ne le sont pas.
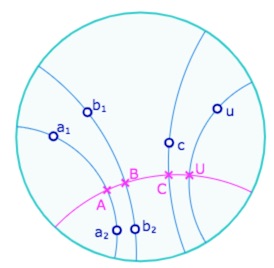
Le cas aligné est immédiat à traiter, en particulier car il n’entre pas dans le cadre de pinceaux sans support (illustration ci-contre).
En effet, dans le cas où \(B, C, U\) sont alignés, les droites \(b_1ac_1\)et \(b_1au_1\) sont toutes deux incidentes à \(A\) et orthogonales à \((BC)=(BU)\). Elles sont donc égales, d’où \(c_1=u_1\). Ainsi \(A, C\) et \(U\)sont sur \(c_1\) et donc les 4 points \(A, B, C, U\) sont alignés \((c_1=u_1=b_1)\) sur la perpendiculaire commune à \(b,c\) et \(u\) (passant par \(A\)). Nous avons \(bca\) est une droite, avec \(b_1 \mid b, c\) et donc, par le théorème 9 réciproque de l’axiome A4, \(b_1 \mid a\). Soit, par l’axiome 4, \(acu\) est bien une droite, ce que l’on voulait montrer.
Revenons au cas général : si \(B, C, U\) ne sont pas alignés, ils forment trois droites distinctes sur lesquelles on peut construire les pieds \(U_1, C_1, B_1\) des perpendiculaires \(u_2,c_2,b_2\) issues de A orthogonales, respectivement à \((BC),(BU)\) et \((CU)\). Par le lemme préliminaire ces points sont encore distincts.

Dans l’illustration ci-contre on n’a pas nommé ces perpendiculaires (en pratique représentées par les segments : \(x_2 = [AX_1]\) pour \(x=u, c, b\)). Nous avons à nouveau trois configurations du théorème de Hjelmslev avec des pinceaux à centres, d’une part issus de \(A\) d’autre part issus respectivement de \(B, C\) et \(U\). On a donc les orthogonalités suivantes :
(*2) \(\quad c_2u_1b_2 \perp (C_1B_1) \quad u_2c_1b_2 \perp (U_1B_1) \quad u_2b_1c_2 \perp (U_1C_1)\)
Mais \(b_1ac_1=u_2\) et \(b_1au_1=c_2\) – par (*1) car les droites sont incidentes à \(A\) – et donc \(u_2c_1=c_2u_1\), soit \(u_2c_1b_2=c_2u_1b_2\) ce qui, injecté dans (*2) permet d’écrire que les trois points \(U_1, C_1, B_1\) sont alignés. Les trois perpendiculaires ci-dessus sont donc identiques et comme les produits sont tous incidents à \(A\) on peut écrire la troisième égalité \(u_2b_1c_2=u_2c_1b_2\) soit \(b_1c_2=c_1b_2\). En réinjectant cette égalité dans \(b_1au_1=c_2\), cela donne \(c_1au_1=b_2\) , et donc que \(c_1au_1 \perp (C_1U_1)\).
Cette dernière orthogonalité s’interprète alors, par une sixième utilisation du théorème de Hjelmslev, cette fois-ci dans le sens réciproque, par le fait que \(cau\) est une droite, ce que nous voulions montrer (à l’ordre prés mais on sait que la nature du produit est indépendant de l’ordre des trois droites).
Cette transitivité de la relation « être en pinceau », obtenue d’une manière générale par six applications du théorème fondamental des plans métriques a comme principal intérêt de s’appliquer aux pinceaux qui ne sont ni « à centre » ni « à axe » comme illustré ci-dessus.
Lancer la figure associée à cette preuve dans un nouvel onglet.
Par ailleurs l’application répétée de cette transitivité donne des expressions importantes plus simples – et plus opérationnelles – sur la notion de pinceau :
Th 15 : théorème général des tri-réflexions
Si \(a, b, c \in \mathscr{P}_{uv}\) alors \(abc\) est une droite.
Le produit de trois droites appartenant à un pinceau est une droite.
Th 16 : réciproque du théorème général des tri-réflexions
Pour \(a \neq b\) si \(a, b \in \mathscr{P}_{uv}\) et si \(abc\) est une droite, alors \(c \in \mathscr{P}_{uv}\).
Si le produit de trois droites dont deux (distinctes) sont dans un pinceau est une droite, la troisième appartient aussi à ce pinceau.
Th 17 : synthèse des deux précédents
Pour \(a \neq b\) si \(a, b \in \mathscr{P}_{uv}\) alors \(\mathscr{P}_{ab} = \mathscr{P}_{uv}\).
Deux droites distinctes déterminent entièrement le pinceau auxquelles elles appartiennent.
Th 18 : intersection de deux pinceaux (en appliquant 2 fois Th 17)
Pour \(a \neq b\) si \(a, b \in \mathscr{P}_{uv}\) et \(a, b \in \mathscr{P}_{pq}\) alors \(\mathscr{P}_{uv} = \mathscr{P}_{pq}\).
Deux pinceaux distincts ont au plus une droite en commun.
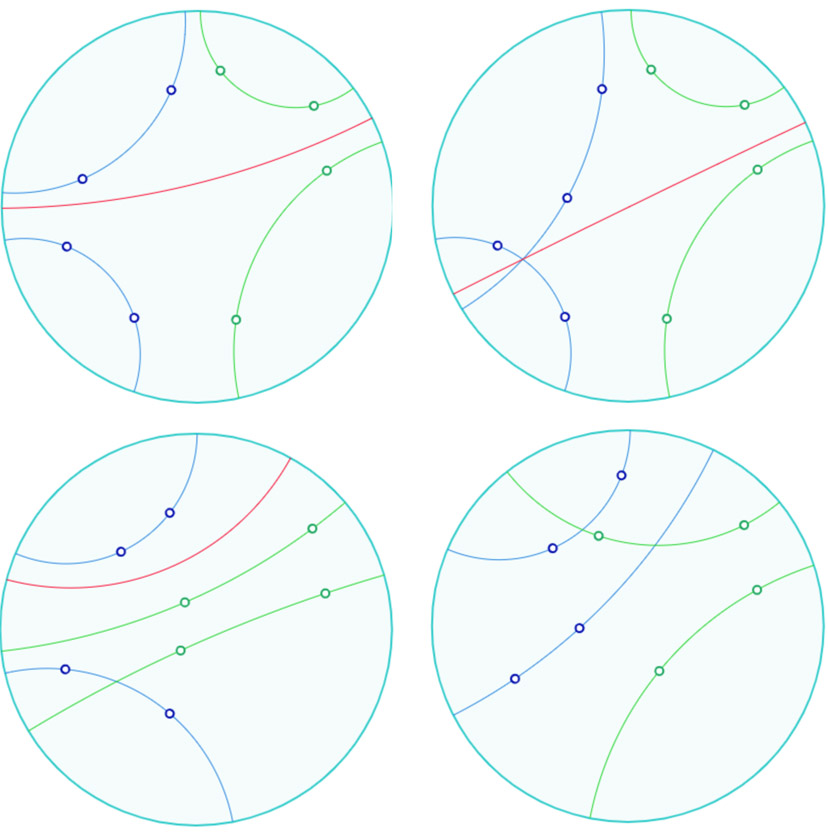
Intersection de deux pinceaux
À gauche : existence de l’intersection de deux pinceaux à axes
À droite : en haut existence avec deux types différents de pinceaux, en bas pas d’intersection
Lancer la figure d’intersection de deux pinceaux dans un nouvel onglet.
D’une manière générale dans le cas hyperbolique, seuls deux pinceaux à axe, comme en bas à droite, peuvent ne pas avoir d’intersection. Dans tous les autres cas (8 autres possibilités en comptant les cas sans support) il y a toujours intersection. Par exemple dans le cas de deux pinceaux sans support, la droite joignant les points idéaux de chaque pinceau est la droite d’intersection.
Th 19 : supplément au Th 15
Si \(a, b, c \in \mathscr{P}_{uv}\) alors \(abc \in \mathscr{P}_{uv}\).
Le produit de trois droites appartenant à un pinceau est une droite du pinceau.
Preuve : si \(a = b\), il n’y a rien à montrer. Sinon, par le théorème 17, on a \(\mathscr{P}_{ab} = \mathscr{P}_{uv}\) donc \(c \in \mathscr{P}_{ab}\). Comme \(abc\) est une droite (th. 15) on peut écrire \(ab.abc=ab.cba=c^{ba}\). Ce produit est donc une droite, c’est-à-dire que \(abc \in \mathscr{P}_{uv}=\mathscr{P}_{ab}\).