La question de la relation d’une géométrie plane métrique avec un plan projectif a, historiquement, deux approches. Tout d’abord celle de Cayley (1854) et de Klein (1869) qui consiste, étant donné le plan projectif, à regarder ce qui se passe à l’intérieur d’une conique. Ensuite est venue la démarche réciproque, initiée par Pasch mais surtout développée par Dehn (1900) qui consiste à partir d’une géométrie plane et à la compléter en un plan projectif par adjonction de points et de droites.
« Pour passer de la notion d’un espace limité à celle de l’espace projectif, il suffit d’adjoindre aux points qui composent l’espace limité de nouveaux éléments convenablement définis auxquels on a donné le nom de points idéaux. […] On les définit en généralisant le concept de « gerbes de droites » […] Lorsque les gerbes ne se rencontrent pas toutes en un même point de la région limitée de l’espace envisagé, on dira que la gerbe est impropre pour cette région et que ses droites ont en commun un point idéal. »
Principes de géométrie – Encyclopédie des sciences mathématiques.
Même si le menu sur l’axiomatique de Bachmann a été rédigé depuis, cette page d’introduction non technique a été conservée. Elle propose quelques illustrations sur ce thème du plongement. Dans son ouvrage de référence, Bachmann montre que son axiomatique, malgré sa généralité, passe bien « le plongement projectif métrique ». On se doute que ce n’est ni immédiat ni élémentaire, et nous allons ici juste illustrer ce plongement avec une figure, très simple, celle des hauteurs d’un trilatère du plan hyperbolique.
Même si elle est très simple, nous allons voir qu’elle illustre bien, dans ce modèle du disque de Poincaré, une vraie généralisation obtenue par ce plongement projectif du plan de Bachmann. Avec son axiomatique nous sommes dans ce que Gonseth appelle « une seconde axiomatisation » , pour laquelle une réflexion logique sur les concepts de la première axiomatisation permet d’élaborer les outils et les objets premiers de la seconde. Bachmann, sur les pas de Hjelmslev a aussi élaboré son plongement dans l’observation du modèle de Klein Beltrami, lui même déjà projectif. C’est d’ailleurs une des macro-constructions de ce modèle qui est utilisée dans ces figures.
Les hauteurs d’un trilatère dans ce plongement
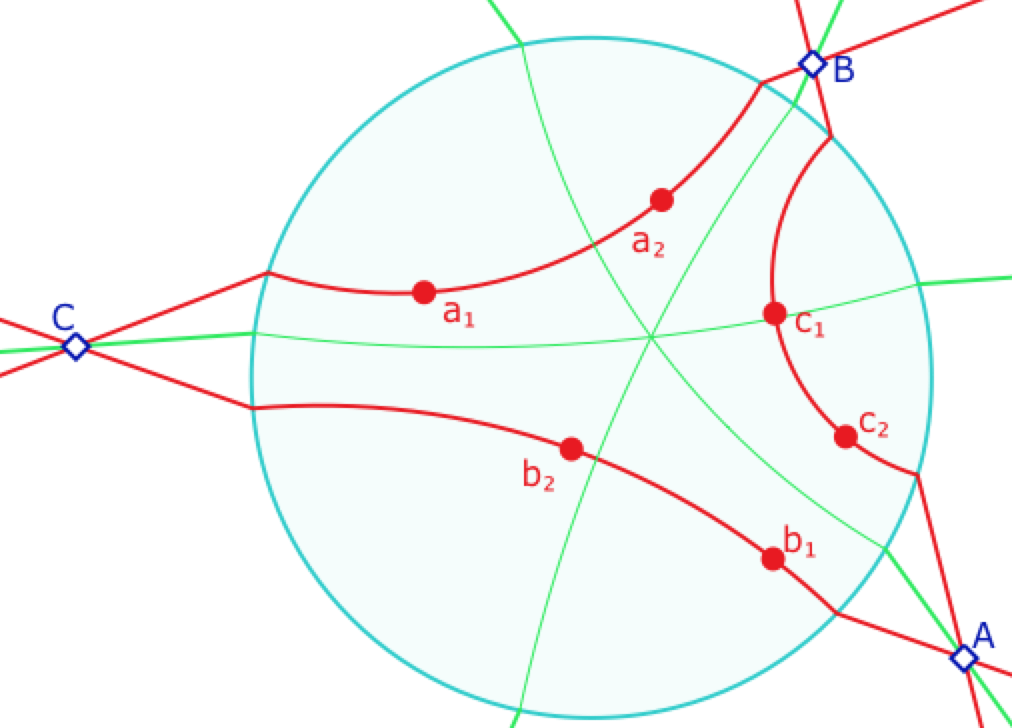
Dans le modèle du disque de Poincaré, le plongement projectif va être représenté par le plan euclidien tout entier : les points du plan euclidien sont les points, dans ce modèle, du plan projectif. Les droites sont le prolongement affine, depuis leurs points idéaux, des droites hyperboliques représentées par les arcs de cercles.
Le trilatère des droites \(a, b, c\) portées deux poignées sur chaque droite, se prolonge en dehors du disque de Poincaré comme illustré ci-contre et forment un triangle \(ABC\) dans le plongement. Et les hauteurs du trilatère sont alors les hauteurs de ce triangle.
Ainsi les hauteurs d’un trilatère du plan hyperbolique ne sont que les hauteurs d’un triangle du plan projectif.
Ci dessous, le trilatère est devenu un triangle hyperbolique. Ses trois hauteurs dans le disque de Poincaré sont en faisceau à axe, mais se prolongent, dans le plongement projectif en trois hauteurs concourantes en l’orthocentre idéal du triangle hyperbolique \(ABC\).
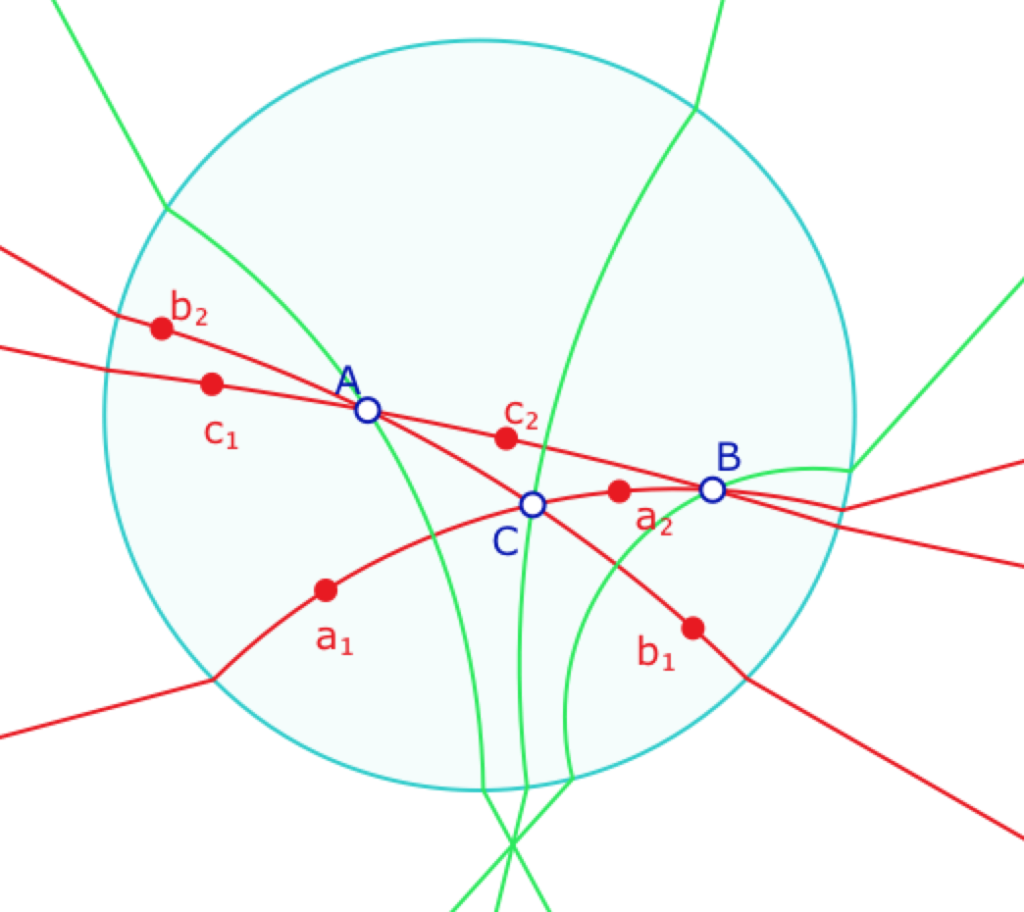
Mais le réel intérêt, qui montre bien la cohérence de ce plongement, est porté par l’illustration suivante. En effet, même si la perpendiculaire hyperbolique à la droite \(c\) issue du faisceau \(F_{ab}\) n’existe pas – ci dessous « celle issue du point idéal \(C\) » – elle a un sens dans le cadre du plongement projectif, ce qui permet d’aboutir à des constructions comme celle-ci où cette hauteur existe désormais mais est une droite idéale du plan projectif.
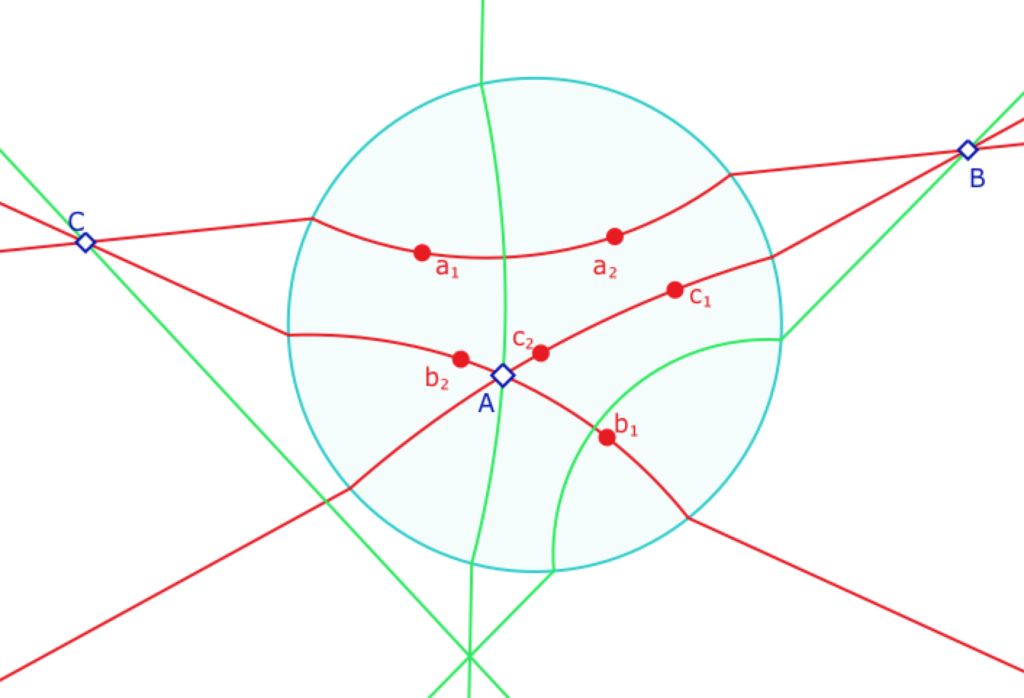
Et les trois hauteurs sont bien entendu en faisceau, et donc concourantes, car dans un plan projectif, il n’y a que des faisceaux à centre.
Paradoxalement l’intérêt de travailler dans le disque de Poincaré est que les droites idéales ne sont pas les droites affines, il y a la «distorsion hyperbolique» pour celles qui traversent le disque. En effet, la construction des droites comme la hauteur issue de \(C\) n’est rien d’autre que la hauteur pour le modèle de Klein-Beltrami – modèle non conforme, antérieur aux modèles de Poincaré, qui est présenté et utilisé dans le menu PS consacré à la pseudosphère et au travail de Beltrami sur ce thème.
Si on avait illustré la géométrie hyperbolique dans ce modèle, le plongement n’aurait été que le prolongement des segments par les droites, ce qui aurait rendu les choses moins visibles. La distorsion des droites apporte sinon plus de sens, au moins plus de visibilité aux problèmes abordés et à leur solutions.
Dans les deux illustrations suivantes, on va un peu plus loin dans l’intérêt de ce plongement projectif. On part d’une situation où une seule hauteur hyperbolique du trilatère existe, et d’un triangle avec un point hyperbolique et deux points idéaux. L’orthocentre est l’intersection du prolongement projectif de la hauteur hyperbolique issue de \(B\) et de deux hauteurs idéales.
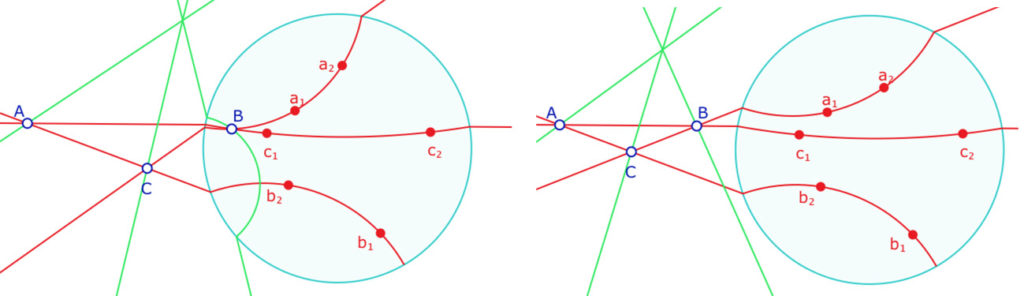
En déplaçant légèrement la poignée \(a_2\), on arrive à une situation où le triangle est entièrement idéal, et pour lequel les hauteurs sont toutes les trois idéales. Le trilatère initial est en effet tel qu’aucune hauteur hyperbolique ne peux exister.
On déplace les droites pour leurs poignées
Préférer ouvrir cette figure dans un nouvel onglet
Dans la page troisième page sur le plongement, consacrée à la polarité, du menu Bachmann, on trouvera une figure plus générale que la précédente.