Même si les droites sont les mêmes, le sens du cercle horizon dans les deux modèles est très différent, entre le modèle euclidien borné, pour lequel le cercle est, de fait, la droite de l’infini, et le modèle elliptique où les points du cercles sont des points elliptiques, mais diamétralement identifiés.
Par construction, le modèle elliptique est conforme : des grands cercles orthogonaux se projettent en des cercles orthogonaux par projection stéréographique.
Utilisation de la représentation elliptique sur la sphère
A une rotation prés, une droite elliptique, comme image d’un grand cercle, peut toujours représenter l’équateur de la sphère. Or toutes les droites orthogonales à l’équateur se coupent au pôle nord. Donc dans le plan elliptique, les droites orthogonales à une droites \((AB)\) passent toutes par un même point, appelé, par analogie, le pôle de la droite.
Autrement dit, pour toute droite, il existe un point tel que toutes les droites passant par ce point sont orthogonales à la droite : par ce point il passe une infinité de perpendiculaires à une droite donnée.
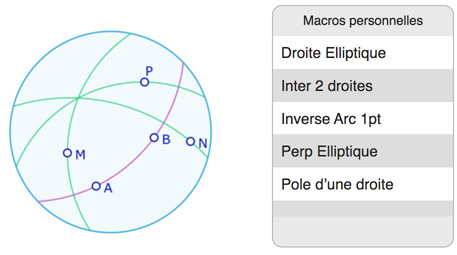
Dans la figure suivante, on vous propose d’utiliser les premières macros elliptiques (ci-contre) pour explorer le pinceau des perpendiculaires. Revoir l’utilisation des macros.
Aspect technique : dans toutes les macro-constructions elliptiques, le premier objet à montrer est le cercle du modèle. Selon les figures, la macro « droite elliptique » peut avoir un nom différent (Drte Alg) car pour économiser les objets dans les macros plus complexes à venir, on a repris le disque unité du modèle euclidien borné.
Exploration du pinceau des perpendiculaires communes
Dans la figure ci-dessous, construire les droites \((AB)\) et \((AB)\), prendre leurs pôles, puis la droite des pôles, et enfin le pôle de cette droite. Étudier la situation, conjecturer et imaginer une preuve – très simple – du résultat.
On peut préférer manipuler la figure déjà finalisée (s’ouvre dans un nouvel onglet)
Dans cette figure, a priori on n’utilise que les macros droite elliptique et pôle d’une droite, mais on peut aussi faire d’autres explorations.
La macro « pôle » est la cinquième donc pas visible dans la liste des quatre premières, il faut faire glisser la liste des macros.
Analyse de la construction précédente : Identification des pinceaux « à centre » et « à axe »

La droite des milieux \((IJ)\) coupe \((AB)\) en l’autre milieu \(E\) de \(A\) et \(B\) que le point \(K\).
Toutes les droites perpendiculaires à \((AB)\) passent par son pôle \(p_{AB}\). Toutes les perpendiculaires à \((CD)\) passent par le pôle de (\((CD)\), le point \(p_{CD}\). Donc la droite \((p_{AB} p_{CD})\) est la seule perpendiculaire commune à \((AB)\) et \((CD)\). Mais cela signifie aussi que ces deux droites se coupent en le pôle de cette perpendiculaire commune. Autrement dit, et c’est bien la spécificité de la géométrie elliptique :
En géométrie elliptique :
• Toutes les droites sont sécantes, et donc il n’y a pas de pinceaux sans support (pas de parallèles).
• Les pinceaux à centre et à axe sont identiques car
• L’intersection de deux droites est le pôle de leur perpendiculaire commune.
Prospective sur cette identité des pinceaux. Première interprétation
Reprenons l’esprit de la preuve du théorème absolu des milieux (vu dans le menu DP). Dans cette prospective, admettons que l’essentiel des propriétés d’essence algébrique soit transférable.
Alors le pinceau à axe utilisé dans la preuve reste comme tel par construction. Il s’ensuit que «la médiatrice du 3° côté est une perpendiculaire commune au 3° côté et à la droite des milieux». La droite des milieux coupe donc le 3° côté du triangle (la droite) en un point (\(E\) ci-contre) qui est le pôle de la médiatrice.
Dire que les pinceaux à axe sont aussi à centre, signifie qu’une droite et un point sont équivalents. Certes pas au niveau des configurations , ce n’est pas le même objet, mais plutôt d’un point vue des isométries.
Autrement dit, la symétrie orthogonale est la symétrie centrale par rapport à son pôle (nous y reviendrons en détail). Ici, la symétrie orthogonale par rapport à la médiatrice échange \(A\) et \(B\) est aussi une symétrie centrale de centre \(E\), qui échange \(A\) et \(B\). Le point \(E\) est aussi un milieu de \(A\) et \(B\), comme le point \(K\).
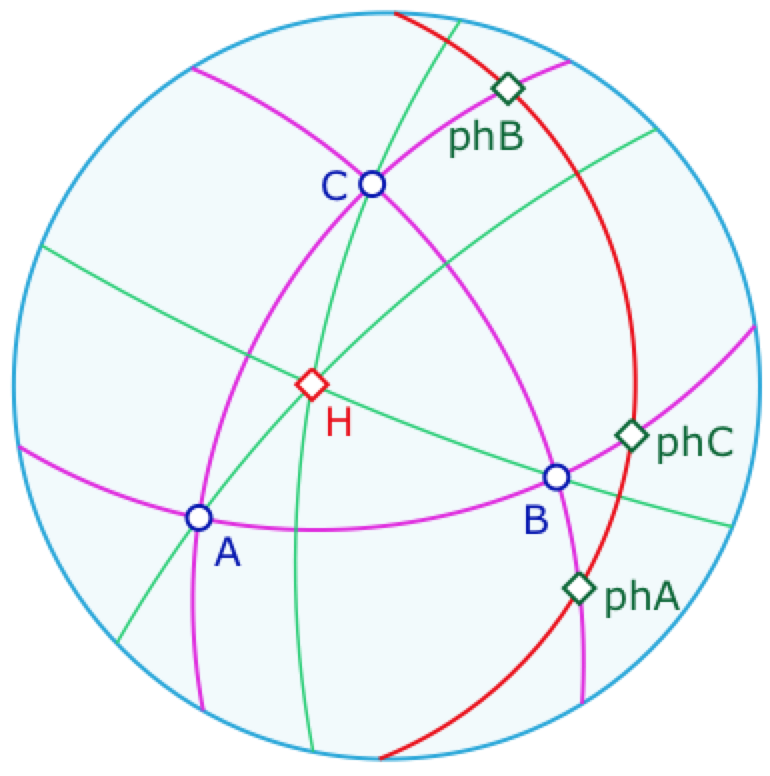
Exercice d’application – Dans la figure suivante, tracer les droites du triangle \(ABC\), puis les trois hauteurs du triangle et les pôles de ces trois hauteurs. Construire la droite passant par deux de ces pôles. Observations et conjectures ? Anticiper le pôle de cette droite avant de le construire. Sur la base de l’existence de l’orthocentre, envisager une preuve de tous ces résultats (immédiate en fait).
On peut, là aussi, préférer consulter cette figure finalisée (dans un nouvel onglet)
La réalisation de cette figure ne nécessite que 3 macros : droite elliptique, perpendiculaire elliptique, et pôle d’une droite
Complément possible : vous pouvez ajouter les pôles de droites du triangle et voir les alignements sous-jacents.
Bilan de l’exercice
Que les hauteurs soient en pinceau est un résultat théorique général, indépendant du type de géométrie. Voici une illustration bien spécifique au cas elliptique
Pour \(\{X, Y, Z\}=\{A, B, C\}\), notons \(ph_X\), le pôle de la hauteur issue de \(X\). Ce point appartient à \((YZ)\) puisqu’il est sur toutes les perpendiculaires à la hauteur issue de \(X\). La droite \((ph_B ph_C)\) est la perpendiculaire commune aux deux hauteurs issues de \(B\) et \(C\). Elles sont sécantes en son pôle, noté \(H\). Si on suppose acquis que les hauteurs sont en pinceau, ici elles sont en pinceau à centre, de centre \(H\). La droite \((AH)\), passant par \(H\), est orthogonale à \((ph_B ph_C)\), mais c’est aussi la hauteur issue de \(A\), donc c’est la perpendiculaire commune à \((BC)\) et \((ph_B ph_C)\). Elles se coupent au pôle de la hauteur issue de \(A\), soit en \(ph_A\).
Ainsi les pôles des trois hauteurs sont alignés … sur la polaire de \(H\).
Complément
On rajoute les pôles \(p_{AB}, p_{BC}, p_{AC}\) des droites \((AB), (BC), (AC)\). Montrer que le pôle \(p_{XY}\) est sur la hauteur \((ZH)\), toujours pour les points \(\{X, Y, Z\}=\{A, B, C\}\). En déduire que la droite \((p_{XY}p_{XZ})\) passe par \(ph_X\), comme ci-dessous, où \((p_{AB}p_{AC})\) passe par \(ph_A\).
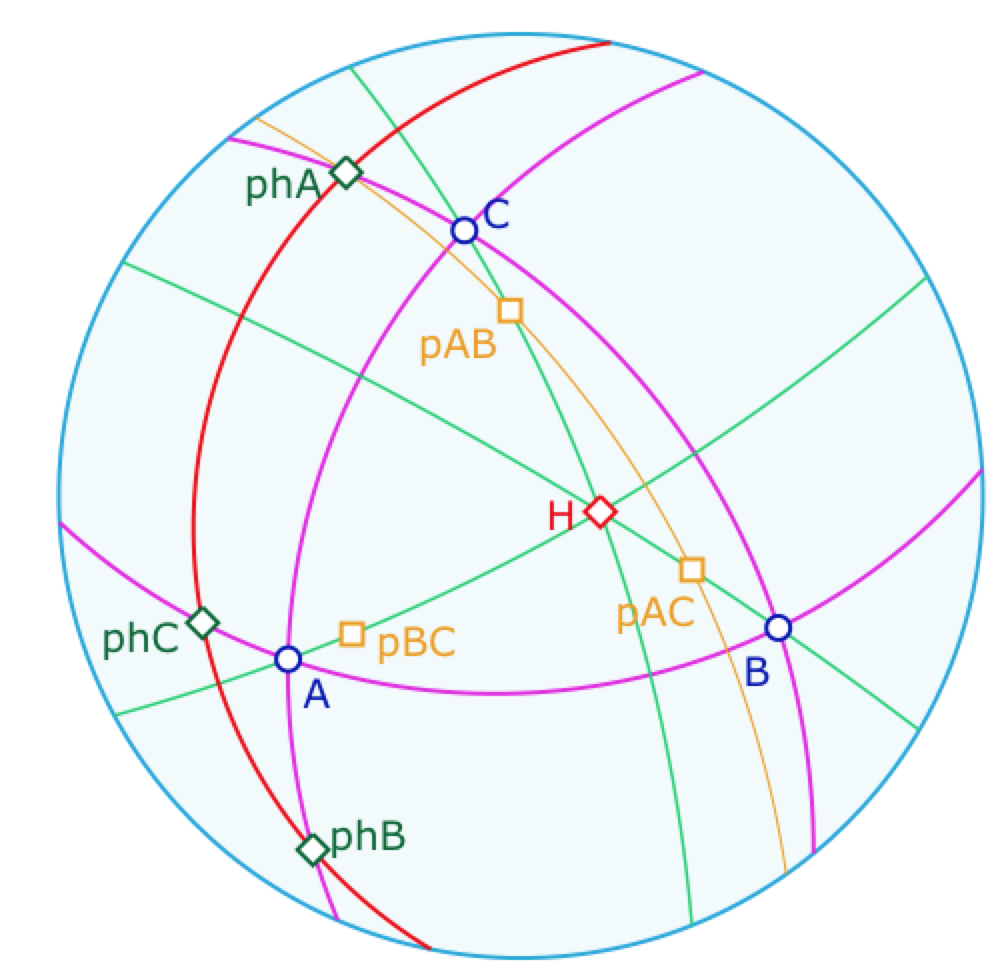
Manipuler en ligne ce complément