Après la présentation de la surface et des premières droites, nous continuons l’illustration de la géométrie hyperbolique sur cette surface si particulière, car elle recouvre une partie bornée du plan hyperbolique, sans accès à l’infini.
Triangles – Cercles
Dans la page précédente, on a vu les médianes, les hauteurs et les médiatrices d’un triangle. On poursuit par le cercle inscrit d’un triangle.
On peut agir sur les sommets \(A, B, C\) ou leurs latitudes \(u_A, u_B, u_C\), mais aussi le paramètre \(p\) et l’orientation de la pseudosphère elliptique (à un doigt ou au clic-déplacer de la souris).
Préférer ouvrir la figure dans un nouvel onglet (être en mode consultation – flèche gauche désactivée – pour tourner la surface).
Et bien entendu la construction « fil rouge » de ce site
On notera que les cercles peuvent ne pas paraître tangents dans certaines configurations. En fait, cela dépend de la façon dont sont finalisées – par le logiciel – les ellipses « KB-cercle » : malgré une grande précision, parfois ce n’est pas « fameux ». Une version « lieu de points » a été tentée, mais trop longue à l’ouverture pour être placée ici.
Préférer ouvrir la figure dans un nouvel onglet.
Orthocentres de trilatères
Un trilatère est défini par six poignées (2 par droites) et donc aussi six latitudes, soit 12 points. On commence simplement par un trilatère de points appartenant tous à la feuille principale. Voici par exemple ce que cela donne pour les hauteurs
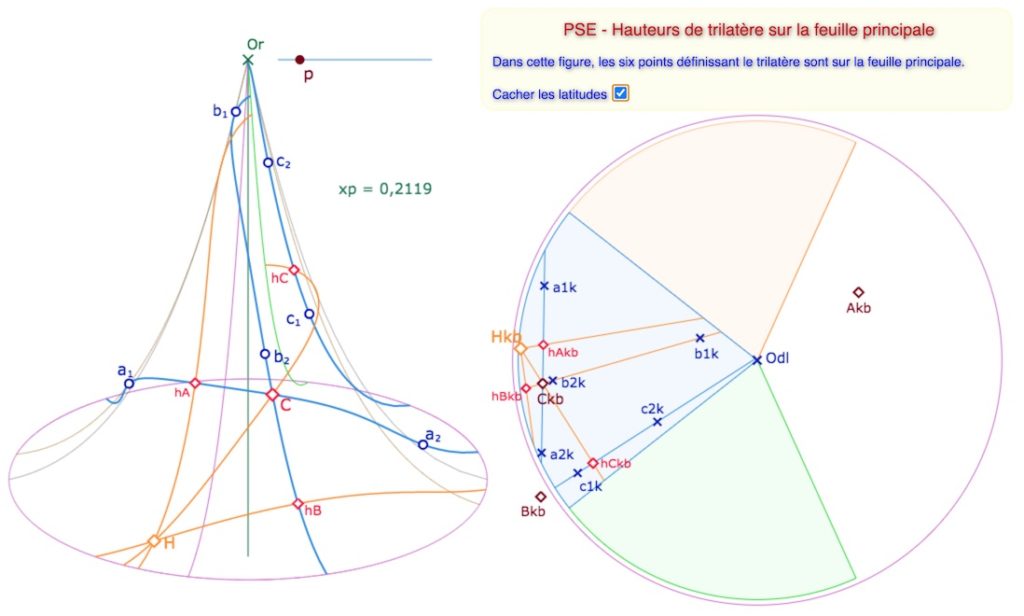
On peut lancer cette figure dans un nouvel onglet.
Mais pour que la figure soit plus intéressante, on choisit de placer chacune des trois droites dans trois feuilles différentes., de la façon suivante :
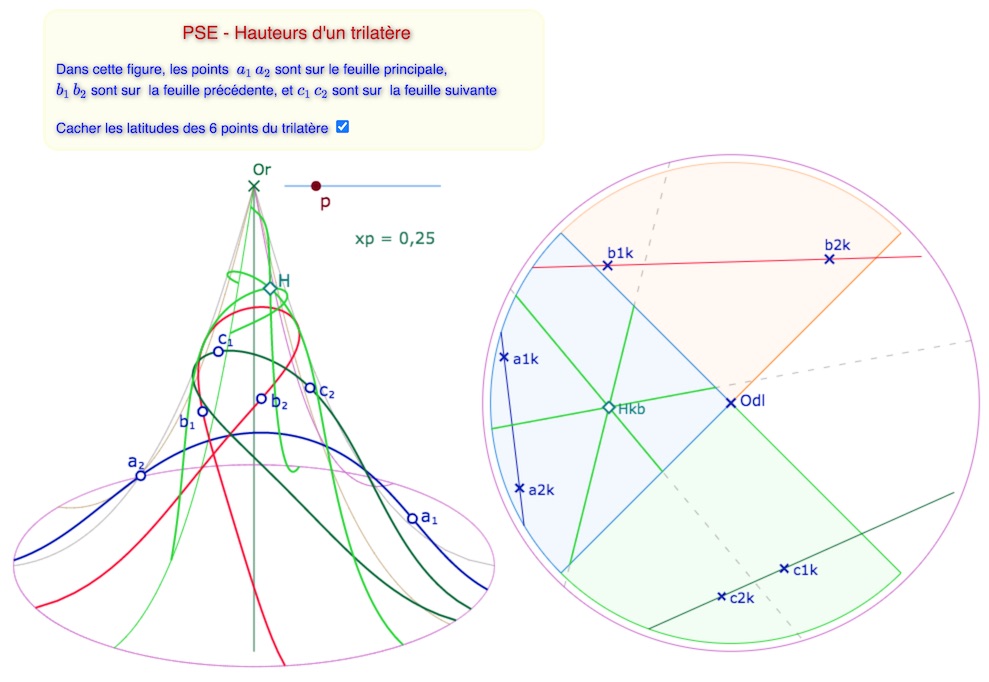
Ci-dessus avec \(p=0,5\). Ci-dessous, avec modification manuelle de \(p=1/3\).
Alors, le cercle image de la PSE est recouvert exactement par ces trois feuilles.
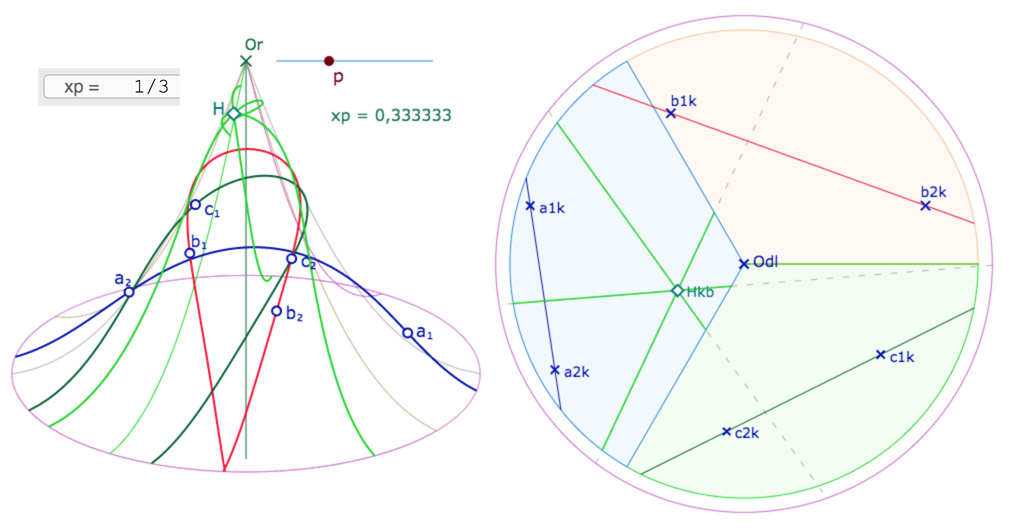
ou encore, toujours avec une modification manuelle, le cas de \(p=0,2\).
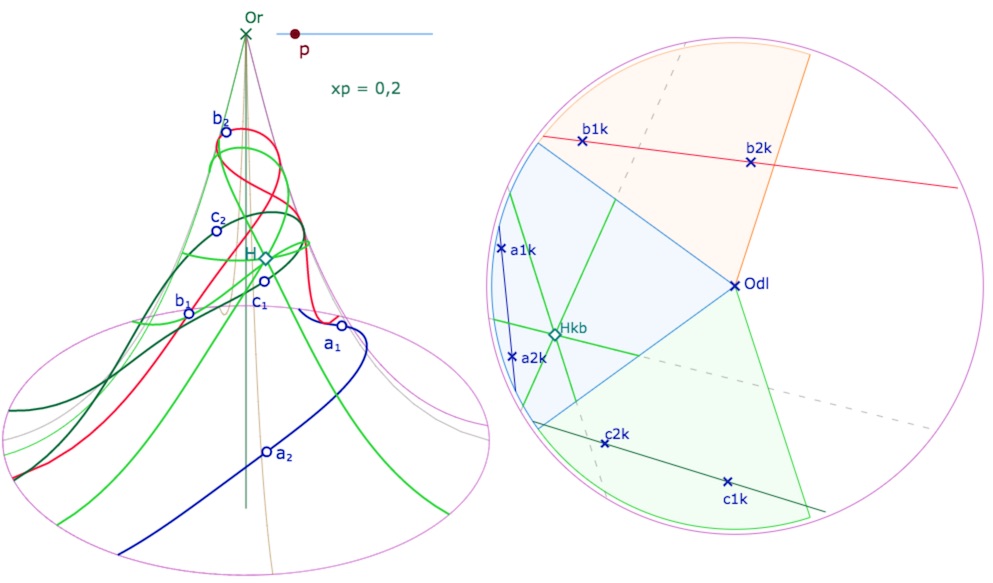
Lancer cette figure des trilatères sur 3 feuilles dans un nouvel onglet.
Comme cette figure est en ligne, on peut modifier \(xp\) manuellement, sans vraiment perturber la figure car il suffit de la recharger pour remettre \(xp\) à son expression initiale \(x(absP)\).
Pour mettre \(xp\) à 0.2 ou 1/3 par exemple ,il faut se placer en mode standard (flèche de gauche active) et sélectionner « calculatrice » en cliquant sur l’expression \(xp\).
On notera que des droites peuvent paraître se couper sur la surface alors que ce point d’intersection n’existe pas car les droites ne sont pas sur la même feuille.
Une figure spécifique de la surface PSE
En manipulant la figure précédente, on voit bien que l’on peut placer l’orthocentre dans KB quasiment sur le centre du cercle, ce qui signifie que l’orthocentre du trilatère, sur la surface, est son point de singularité, soit le point \(Or\). On se propose de réaliser cette configuration. Si l’orthocentre est le point de singularité, cela signifie que les trois hauteurs sont des méridiens. Il y a de (très) nombreuses façons de construire une telle figure. On se propose de se donner trois points de base dans KB.
Voici les choix effectués
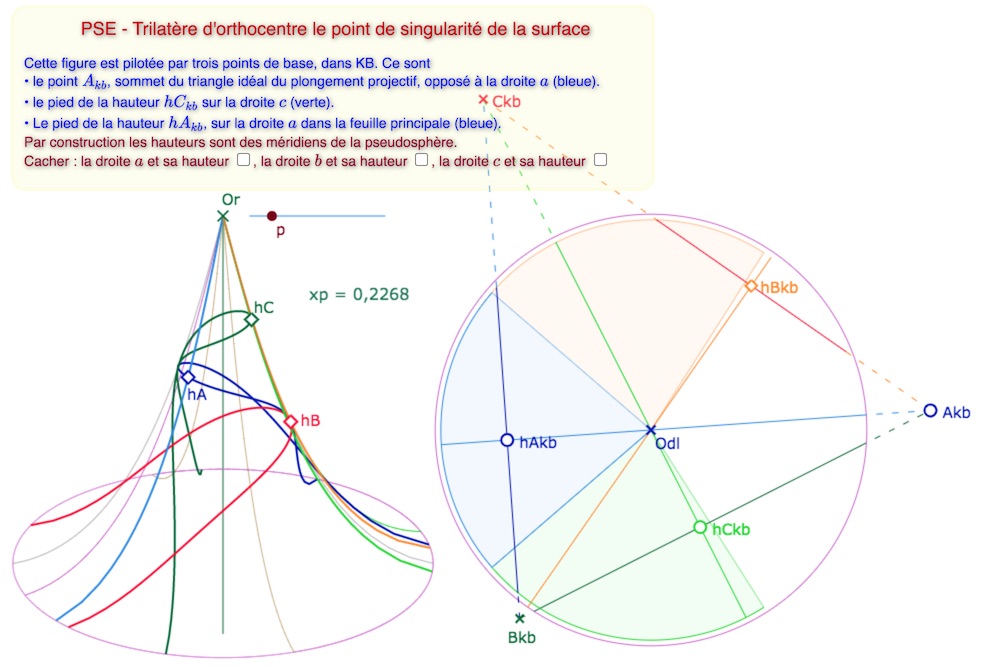
Ci-dessus, détail des choix et vue de face – Ci-dessous deux vues de dessus, très limpides
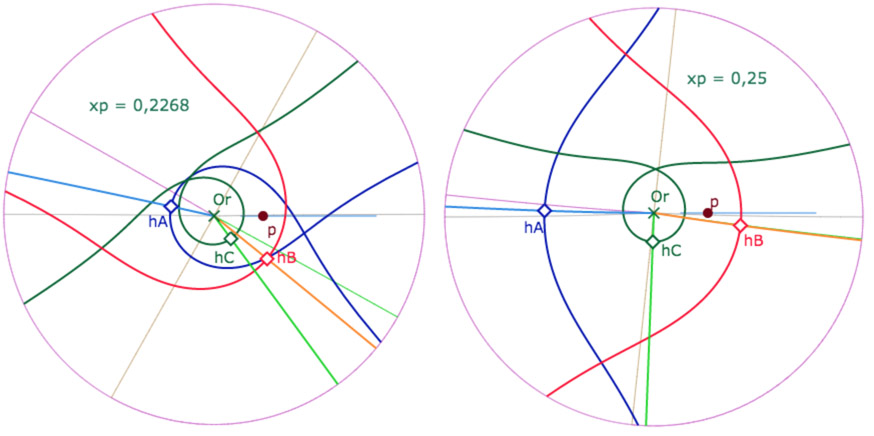
Comme la figure est un peu grande (à cause du point \(A_{kb}\) à droite) on propose de l’ouvrir dans un autre onglet. On peut agir sur les trois points \(A_{kb}, hC_{kb}\) et \(hA_{kb}\).
Commentaires techniques et conseils d’utilisation
• La figure est facile à réaliser car les KB-perpendiculaires à un diamètre sont les perpendiculaires euclidiennes et une KB-perpendiculaire issue du centre \(O_{dl}\) est une perpendiculaire euclidienne.
• Sans entrer dans les détails, le point de base \(A_{kb}\) est nécessairement un « point flottant », c’est-à-dire indépendant de la rotation 3D de la PSE, et il est donc totalement indépendant du centre \(O_{dl}\). Si on déplace \(O_{dl}\), il peut être nécessaire de le déplacer aussi, sinon \(hB_{kb}\) peut ne pas exister.
• De préférence – quand on modifie \(xp\) par exemple – laisser \(hC_{kb}\) dans la feuille verte. \(hC_{kb}\) est sur le cercle euclidien de diamètre \([O_{dl} \, A_{kb}]\).
• Rappel : on tourne la pseudosphère en mode consultation, flèche à gauche inactive.
On peut aussi, comme à la figure précédente, modifier le paramètre \(xp\) de manière manuelle. En voici deux illustrations
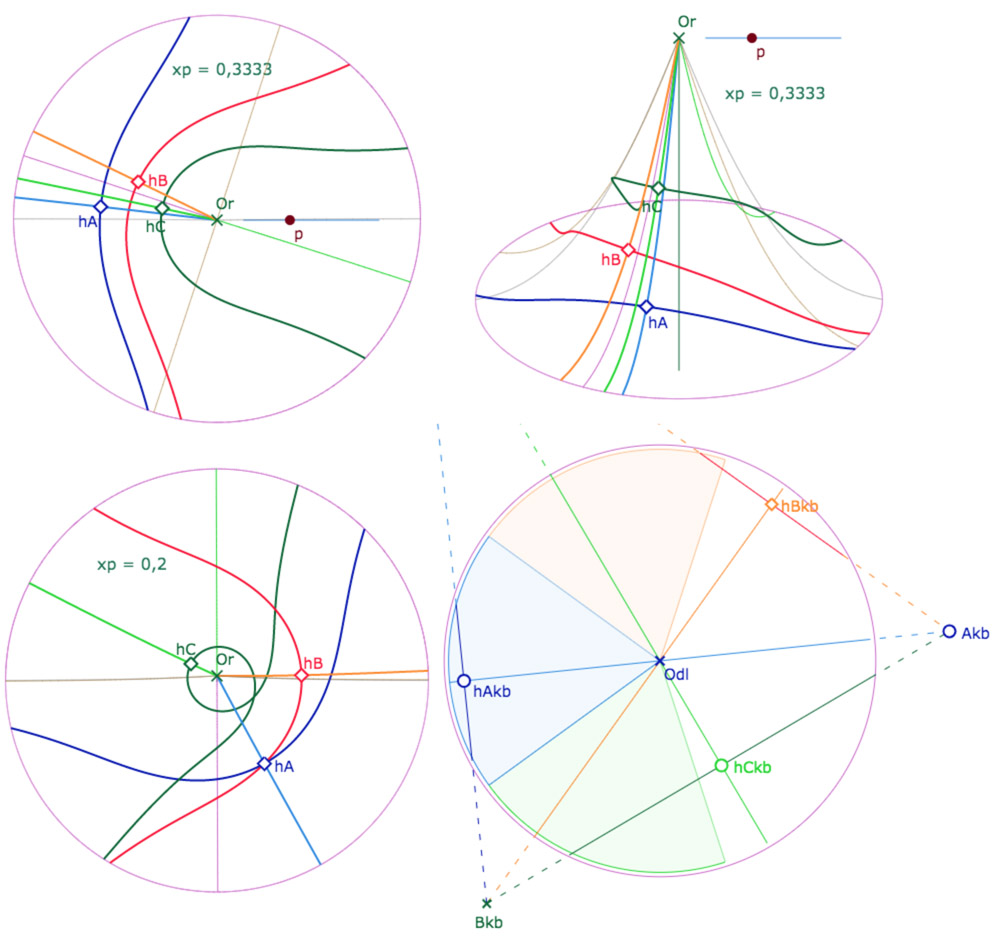
Pour simplifier la manipulation, voici une figure avec xp manuel (s’ouvre dans un nouvel onglet). Ayant la flèche gauche du tableau de bord activée, il sufit sélectionner \(xp\) et de choisir l’outil calculatrice pour en modifier la valeur numérique. Dans cette figure on a caché le curseur du paramètre \(p\).
Le triangle orthique de ce trilatère d’orthocentre le point de singularité
On peut poursuivre l’illustration de cette situation propre à la PSE en construisant le triangle orthique associé. On sait que le centre inscrit du triangle orthique est l’orthocentre du triangle. Ici,dans KB, comme le centre du cercle inscrit est le point \(O_{dl}\), le KB-cercle inscrit est un cercle euclidien, là encore, plus simple à envoyer sur la PSE. On a adapté une figure à cette situation, avec de nombreuse options. Le cercle inscrit sur la PSE est petit, il faut une valeur de \(p\) assez grande (comme 0,5 ci-dessous) pour que l’on voit bien les contacts. Mais on peut les regarder un par un en cachant toutes les autres données.
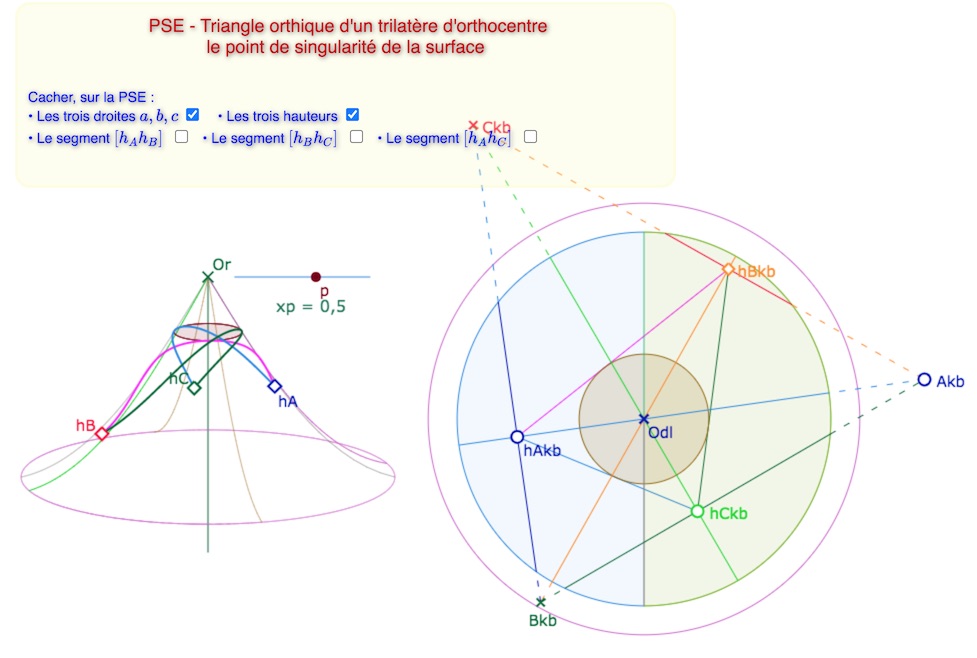
Ci-dessus les options de la nouvelle figure. On voit aussi que pour p=0,5 les côtés du triangle orthique sont monofeuille.
Ci-dessous, vue de dessus, pour p=0,25 les côtés sont tous multifeuilles
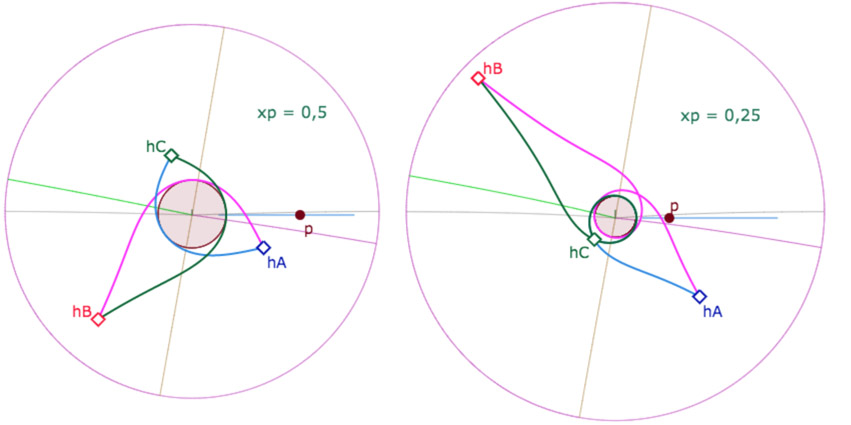
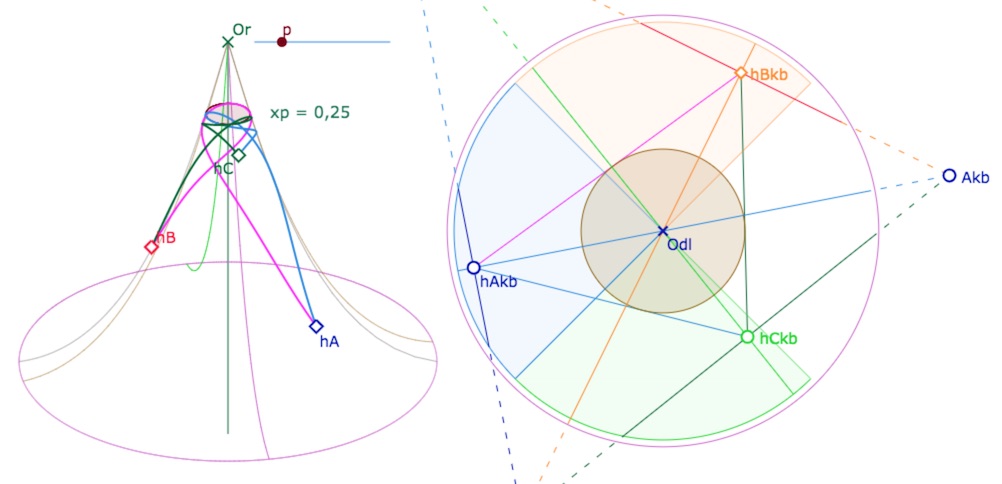
État de la figure suivante à l’ouverture. On agit toujours sur \(A_{kb}, hC_{kb}\) et \(hA_{kb}\)
Ouvrir cette figure dans un nouvel onglet.
Cercle inscrit d’un trilatère tri-feuille
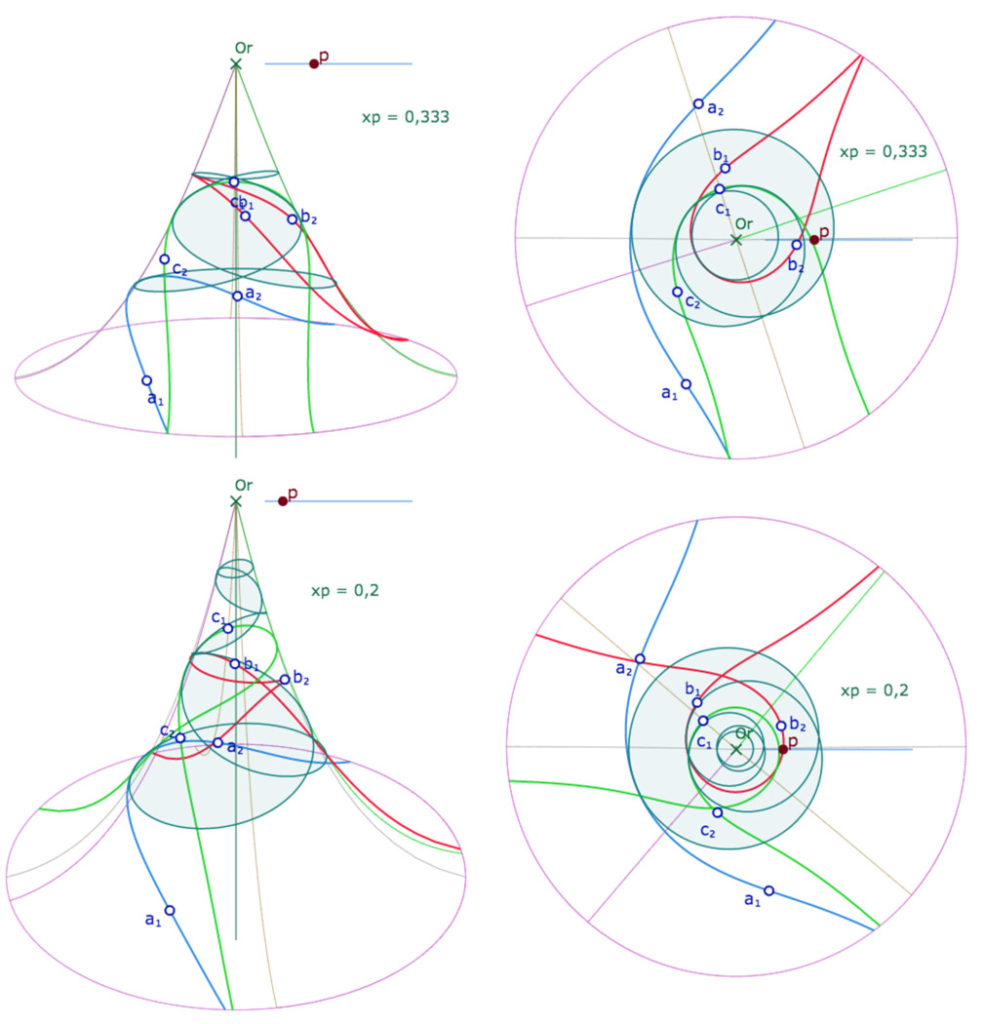
Par construction, le cercle inscrit est multifeuille, comme le cercle image de la PSE. Par exemple pour \(p=0,25\), le cercle est sur 4 feuilles, ce qui produit de jolies figures.
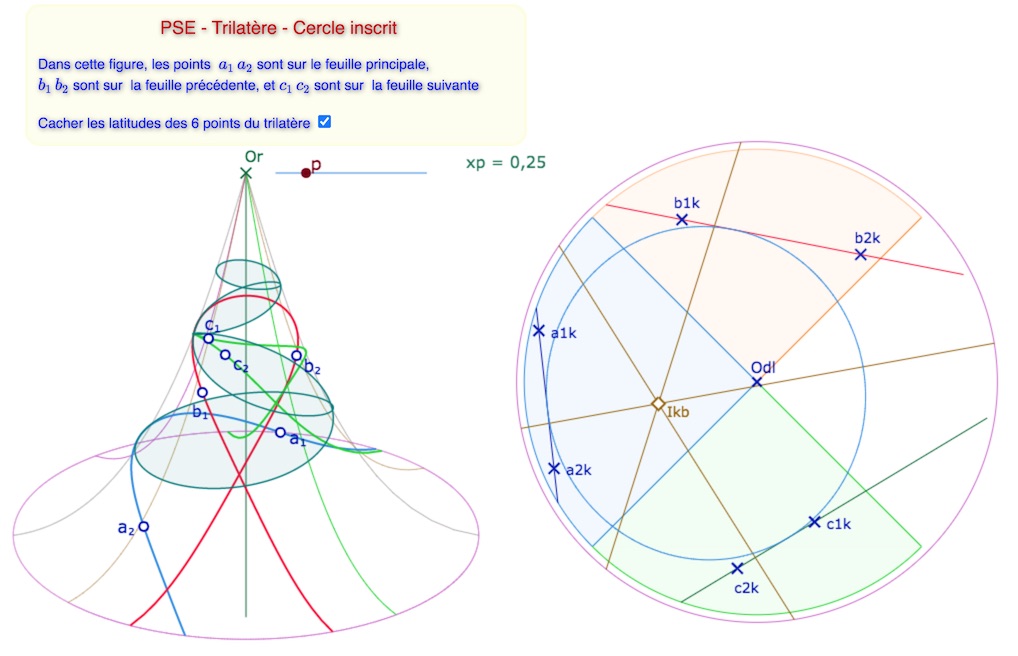
Dans la vue de dessus, on voit bien le contact du cercle avec chaque droite, sur des feuilles différentes
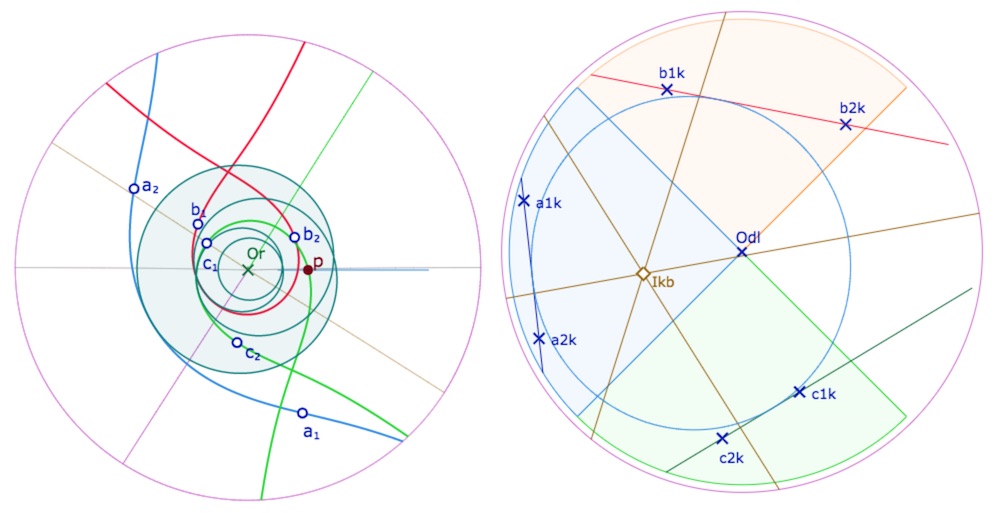
Et, comme pour les hauteurs, on peut choisir de modifier manuellement les valeurs de \(p\) pour des cas particuliers. La modification manuelle n’est disponible que dans la figure ouverte hors du site (en mode standard)
Manipuler la figure
Préférer ouvrir cette figure dans un nouvel onglet (nécessaire pour modifier le paramètre \(p\) manuellement)
Le pentagone orthogonal
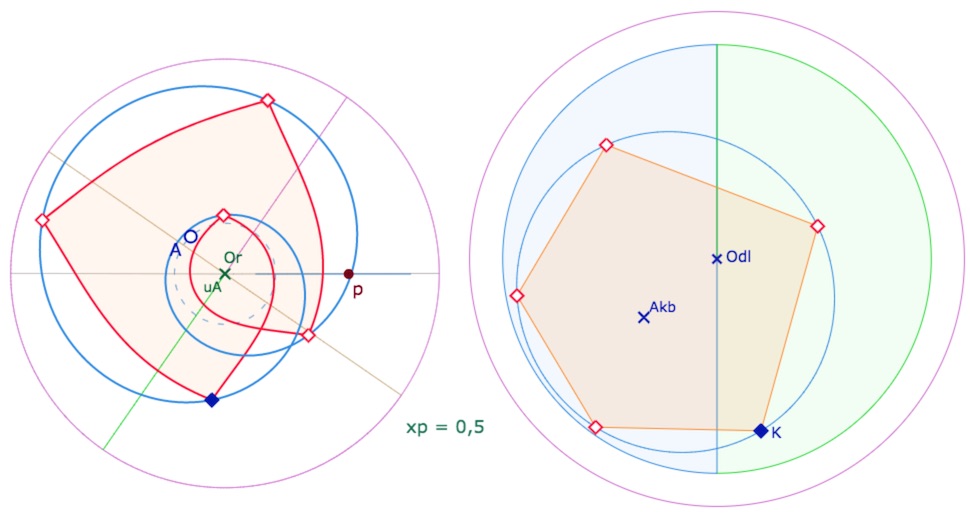
La construction est classique, elle a été présentée sur les deux autres surfaces pseudosphèrique – d’abord en détail sur la pseudosphère, puis plus rapidement sur la PSH. On rappelle qu’il n’y a qu’un rayon de cercle, celui du pavage de P54, mais selon la position du centre, ce cercle circonscrit au pentagone peut être sur une seule ou sur plusieurs feuilles de la PSE. Par exemple ci-dessous, deux illustration pour \(p=0,25\).
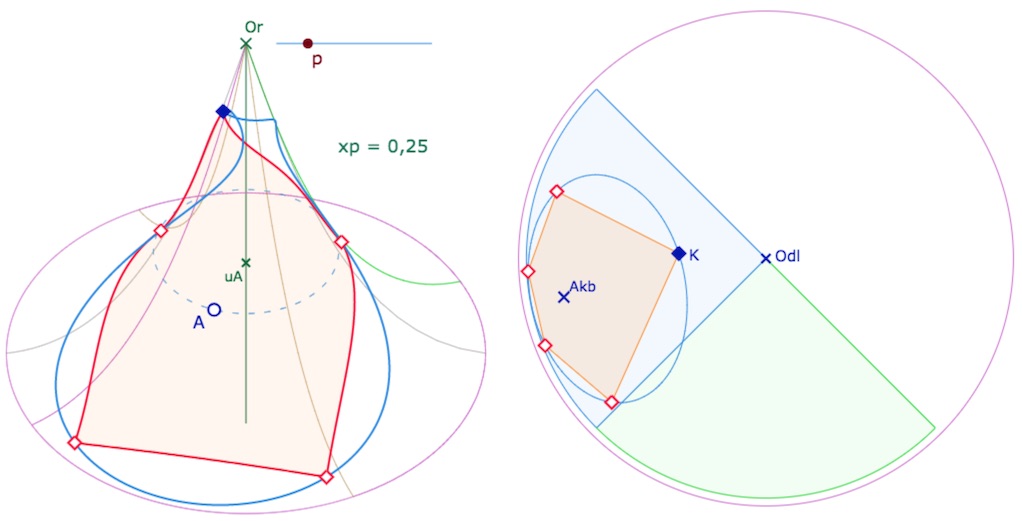
Ci-dessus avec une latitude plus grande (en valeur absolue) pour que le cercle circonscrit s’approche du bord de la PSE : ce cercle est monofeuille – car il n’est pas croisé.
Ci-dessous, avec la même PSE – même valeur de \(p\) – mais une latitude différente. Le cercle est plus loin de la frontière de la surface, et le cercle est sur deux feuilles – croisé.
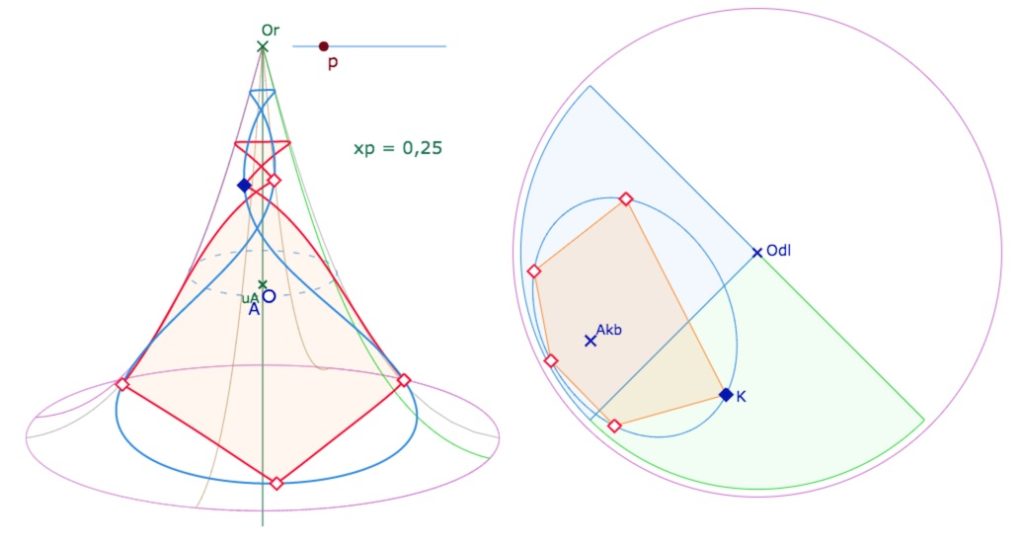
Par contre, pour \(p=0,5\), il n’est pas possible d’avoir un cercle de circonscrit sur une seule feuille.
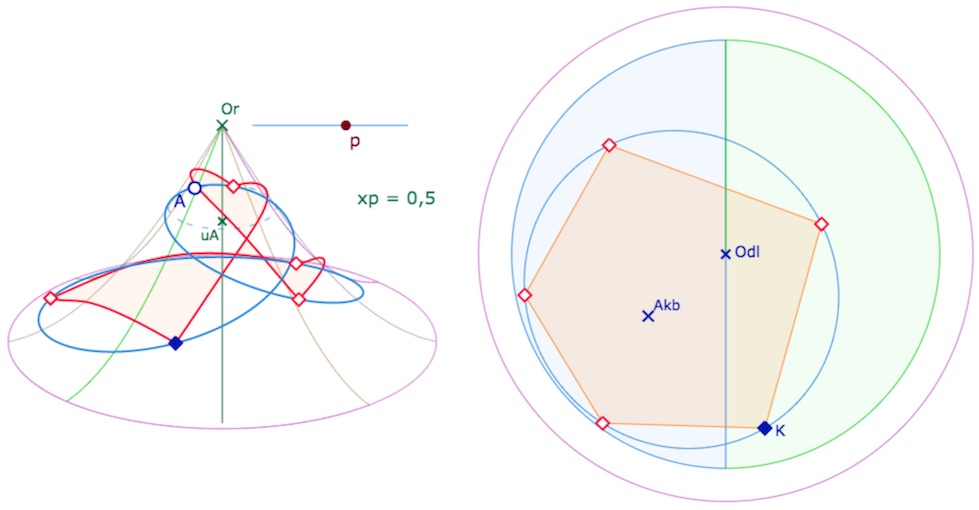
Vue de face et de dessus – dans la même configuration – pour \(p=0,5\)
Manipulation de la figure
Préférer ouvrir la figure dans un nouvel onglet
Pentagone orthogonal centré au point de singularité
Puisque la projection privilégie le centre du disque de Beltrami, on peut s’amuser à construire le pentagone orthogonal associé.
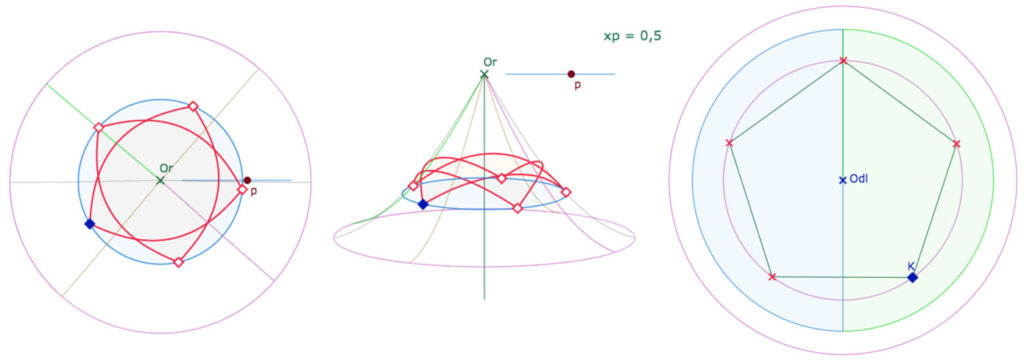
Préférer ouvrir la figure dans un nouvel onglet