Un autre modèle euclidien borné mérite d’être cité pour – rétrospectivement – l’importance historique qu’il a eu lors de la découverte de la géométrie hyperbolique par Bolyaï et Lobachevsky. il s’agit de la sphère privée d’un point \(I\) pour lequel les points du plan euclidien sont les points de la sphère autre que le point \(I\), et la droite passant par deux points \(A\) et \(B\) est le cercle circonscrit aux points \(A, B, I\). Étudiant ce qui allait devenir la géométrie hyperbolique, Bolyaï et Lobachevsky ont tous les deux été amenés à introduire une structure que l’on appelle horisphère (nom donné par Lobatchevsky), une variante de sphère hyperbolique dont le centre est le point idéal \(I\). Alors la géométrie de ces horisphères est intrinsèquement euclidienne : un pont était tracé entre la consistance de la géométrie hyperbolique et celle de la géométrie euclidienne.
Et dans le modèle du disque de Poincaré, l’horisphère de Bolyaï correspond à la géométrie que nous présentons ici.
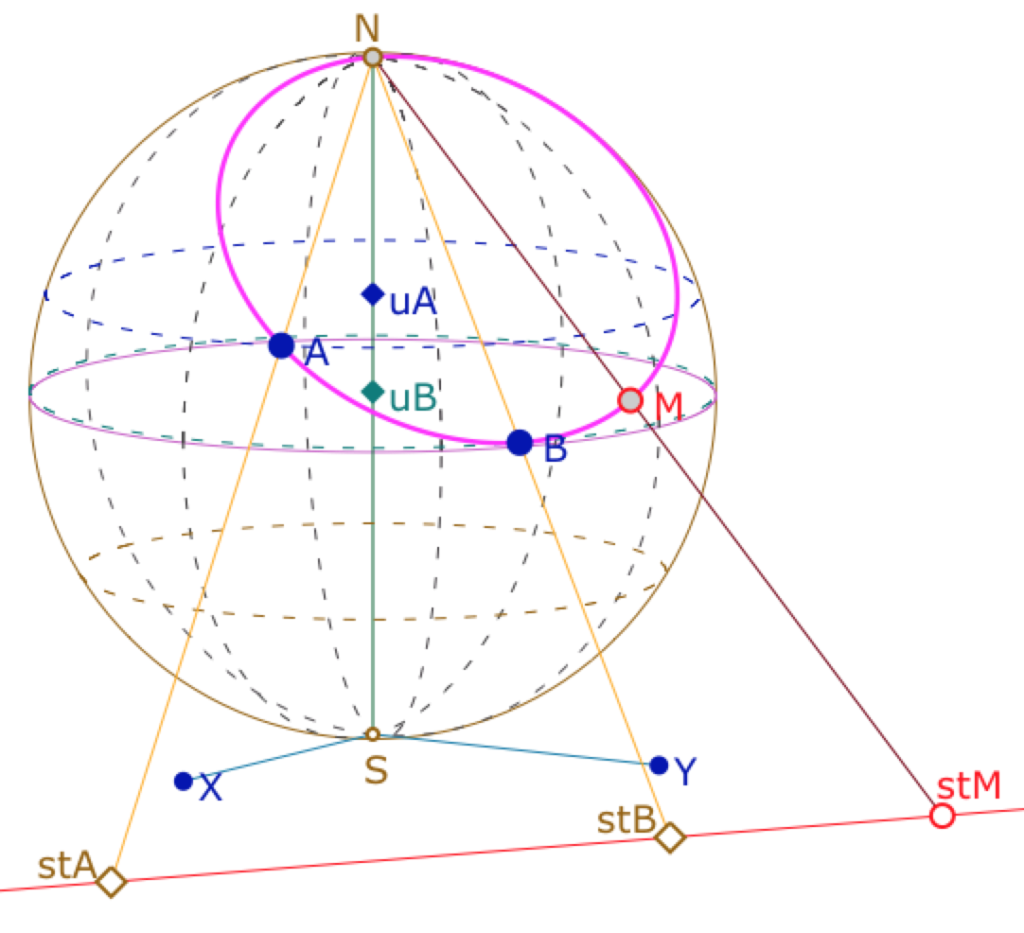
De manière plus rapide, on présente maintenant ce modèle avec la projection stéréographique : ci-contre une sphère de rayon 1 posée sur le plan, à l’origine du repère, on projette un point \(A\) de la sphère sur le plan par son intersection avec la droite \((NA)\) où \(N\) est le pôle nord de la sphère (le point \(I\) de Bolyaï).
Par la procédure inverse, on envoie ainsi tout le plan euclidien sur la sphère privée du pôle nord. Pour deux points \(A\) et \(B\) de la sphère, la droite \((AB)\) sur la sphère est le cercle passant par \(A, B\) et le point \(N\), pôle nord de la sphère, privé de \(N\). Indépendamment des rappels historiques, c’est un autre modèle borné, dans l’espace, de la géométrie euclidienne plane.
Les constructions associées à un triangle se font par conjugaison : on peut manipuler trois points sur la sphère, par leurs côtes uX et leurs positions sur le parallèle associé à uX. On projette ces trois points sur le plan (XSY). Puis on construit la figure affine voulue, et on renvoie le résultat.sur la sphère. Voici quelques illustrations :
a – La parallèle à une droite passant par un point
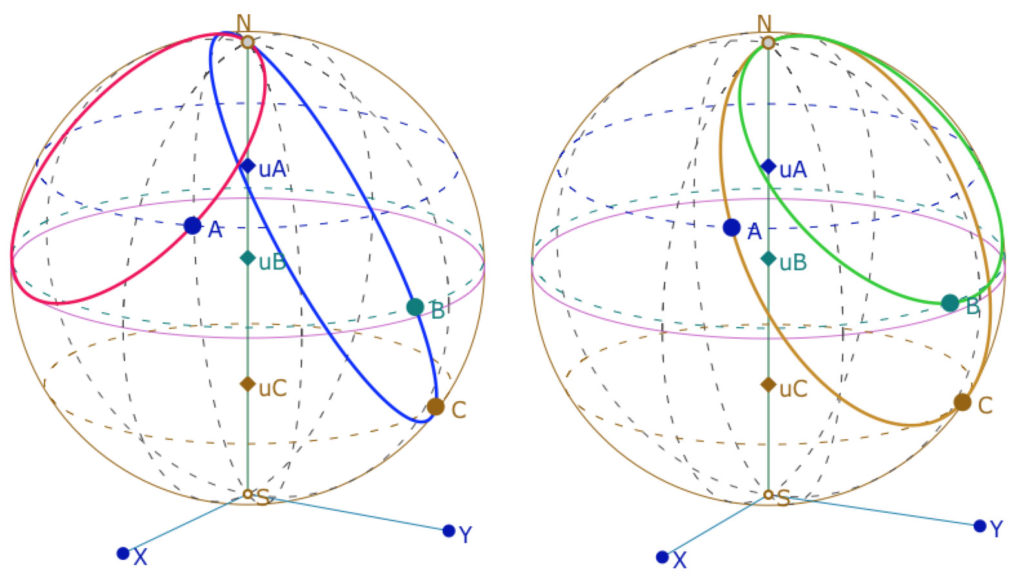
b – le théorème des milieux
(cela se voit mieux sur la figure ci-dessous, en faisant pivoter la sphère)
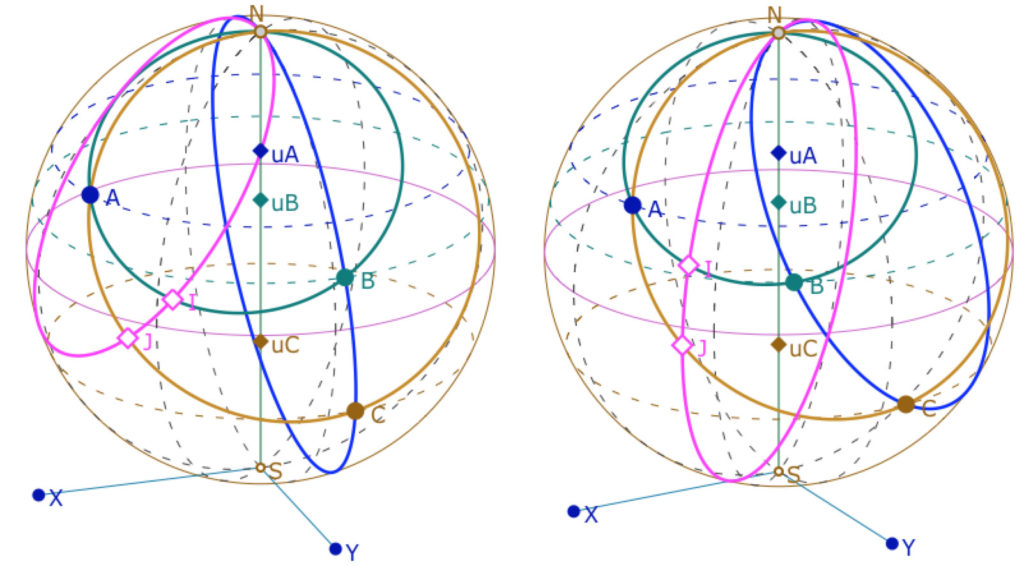
c – le cercle circonscrit d’un triangle
Pour les figures euclidiennes, on renvoie le plan du sol \((XOY)\) sur le plan de l’écran \((YON)\). On effectue une double conjugaison. En pratique on utilise des macros qui vont directement de la sphère à l’écran et réciproquement.
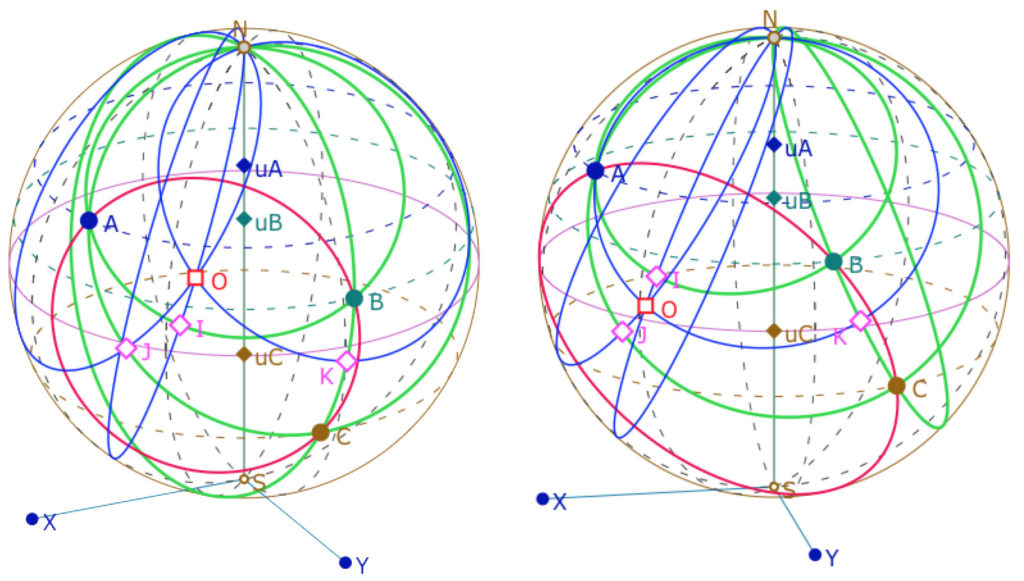
\(I, J\) et \(K\) des côtés et en rouge le cercle circonscrit de centre \(O\).
d – le cercle inscrit d’un triangle
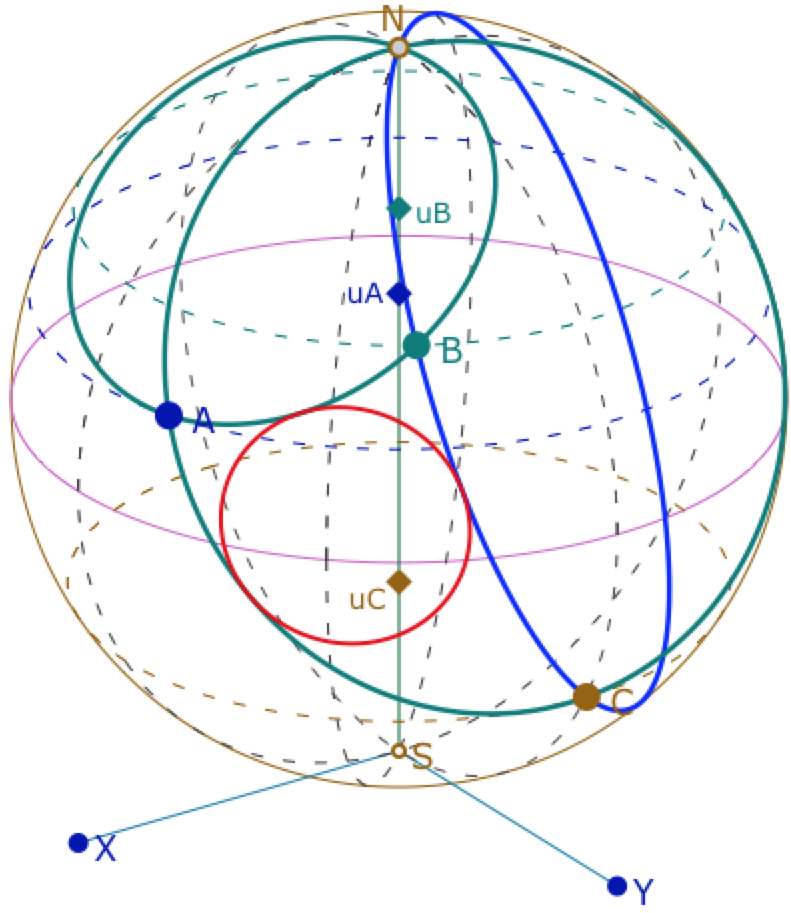
Déplacer les points de base \(A, B, C\) sur leurs latitudes, et changer les latitudes par \(u_A, u_B\) ou\(u_C\).
Préférer ouvrir cette figure dans un nouvel onglet
Le théorème de Feuerbach
Dans la figure suivante, on reprend ce classique euclidien. Dans une version 3D, c’est intéressant d’observer le point de contact des cercles exinscrits et du cercle d’Euler. Voici deux copies d’écran de ce que l’on peut réaliser avec cette figure :
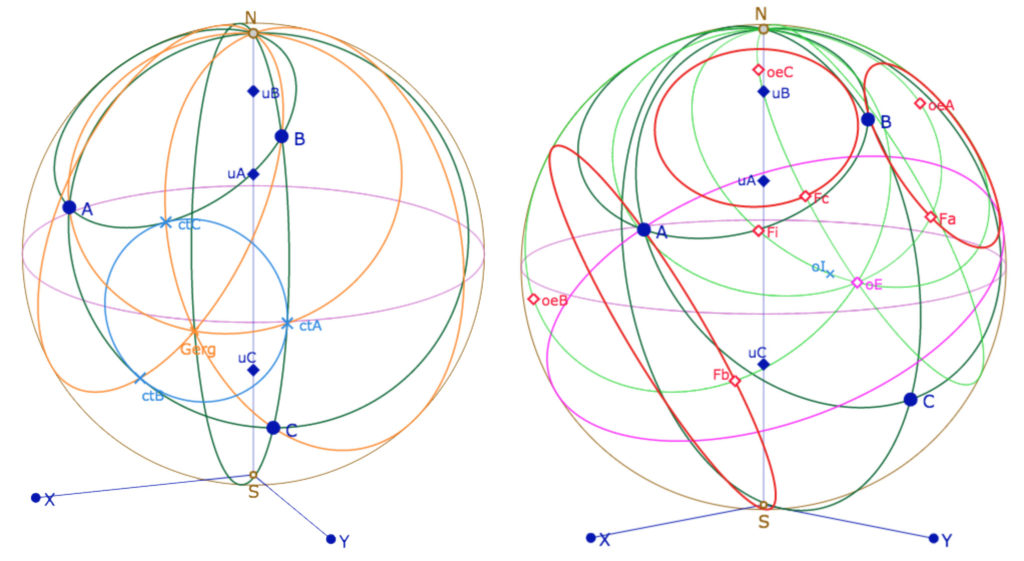
Jouer avec les différentes options de la figure. Penser à faire tourner la sphère
Préférer ouvrir cette figure dans un nouvel onglet (être en mode consultation)
Revoir l’infini de près
On a présenté, dans cette page, la version bornée plane de la parabole tritangente à un triangle.
Brièvement, la parabole de foyer un point M du cercle circonscrit à un triangle et de directrice la droite de Steiner associée à \(M\) est tritangente aux trois côtés du triangle. Dans une version bornée, la parabole passe par un point infini.
Le modèle de l’horisphère n’ayant qu’un point infini, la parabole touche l’infini en le pôle nord \(N\) de la sphère. C’est donc une nouvelle façon de « voir l’infini de près ».
Dans les illustrations suivantes, \(M\) est un point du cercle circonscrit au triangle \(ABC\), le cercle bleu passant par \(N\) est la droite de Steiner associée à \(M\) et la courbe rouge est la parabole tritangente aux trois côtés du triangle.
Comme il n’y a qu’un point à l’infini, la parabole prend de formes différentes selon la position du foyer sur le cercle circonscrit.
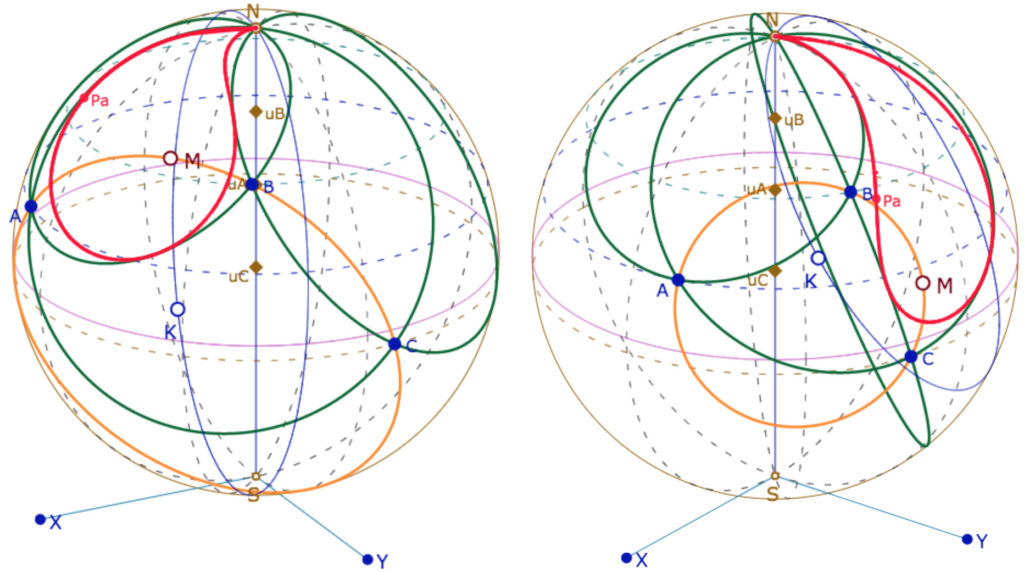
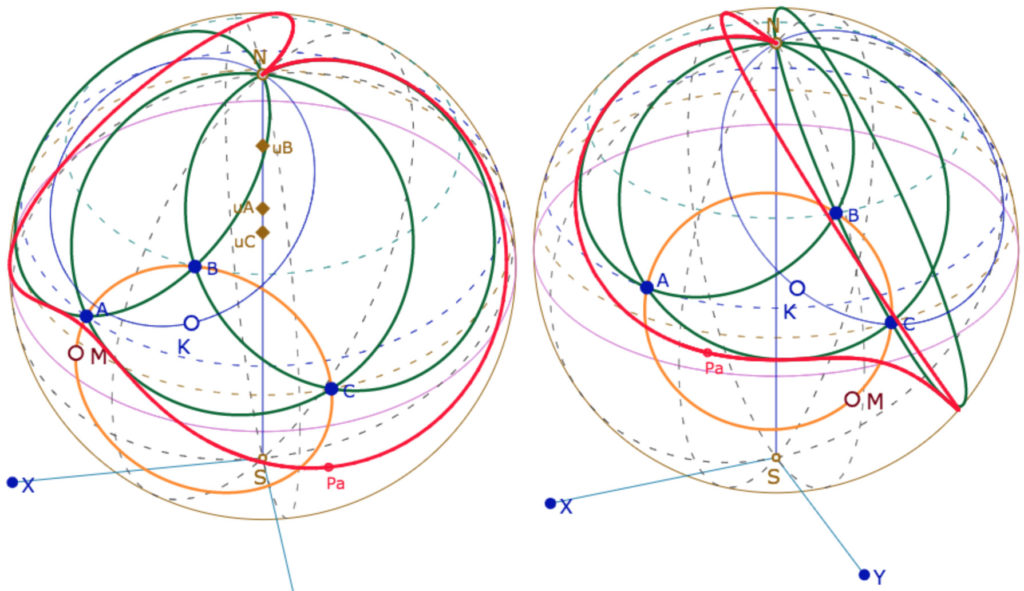
Et bien entendu … la construction de Malfatti
Même remarque que les figures précédentes
Préférer ouvrir la figure (sans restriction) dans un nouvel onglet.
Le seul vrai travail à faire est de construire les outils euclidiens dans le plan \((XSY)\). Pour cela on fait une seconde conjugaison entre les coordonnées dans le plan \((XSY)\) et le repère «écran» du logiciel. La construction de Malfatti se fait donc très simplement par double conjugaison dont on voit la trace sur cette copie d’écran :

La seconde conjugaison envoie le triangle stAstBstC vers un triangle du plan de l’écran.
Une macro fait la construction de Malfatti, et on renvoie dans le plan (XSY) les seuls points nécessaires
à la constructions finale (les centres des cercles et un point de chaque cercle).