Historiquement, une première classification des principales géométries en trois grandes familles a été proposée par Klein en 1872, sur la base de géométries induites d’une géométrie projective métrique (au sens d’une distance) par le procédé de Cayley et de sa conique absolue. Lors de son travail autour des « Fondements de la Géométrie », Hilbert a demandé à Dehn de travailler sur le rôle de la continuité. La principale question à résoudre était de savoir si on pouvait construire une géométrie dans laquelle la somme des angles d’un triangle était supérieure à deux droits, tout en ayant une infinité de « parallèles ». On savait, depuis Legendre que c’était impossible si le corps était archimédien. Dehn mit alors en évidence deux résultats intéressants que l’on peut résumer dans le tableau suivant :
Tout d’abord, il met en évidence l’existence d’une géométrie non elliptique dans laquelle la somme des angles d’un triangle est supérieure à deux droits et pour laquelle il existe une infinité(*) de droites issues d’un point donné, non sécantes à une droite donnée. Cette géométrie est appelée non legendrienne, en référence à la preuve de Legendre utilisant l’archimédie de \(\mathbb{R}\) pour montrer l’impossibilité de cette géométrie. Un sous-produit, alors assez inattendu, est l’existence d’une géométrie ayant cette même propriété quant aux non sécantes mais dans laquelle la somme des angles d’un triangle est égale à deux droits : une géométrie dite semi-euclidienne.
Ce bref rappel historique d’une des problématiques de l’école de Hilbert fixe les points significatifs que nous allons retrouver d’une autre façon dans l’approche de Bachmann, et en particulier cette géométrie semi-euclidienne qui, par certains aspects est proche de l’euclidienne et par d’autres s’en éloigne sensiblement. Par exemple une conséquence troublante de son existence est dans le fait que l’axiome des parallèles et l’alignement des points de l’équidistante ne sont pas des propriétés équivalentes : elles ne le sont, en définitive, que dans cette hypothèse de continuité.
(*) une infinité car les corps utilisés sont implicitement infinis. Plus généralement, le vocabulaire, de cette introduction à la séparation des géométries, est celui de l’époque où ces questions ont été posées, en particulier, les termes « elliptique, euclidienne, hyperbolique » contiennent les axiomes de continuité. Dans les « Fondements » de Hilbert, on distingue plusieurs axiomes de continuité dont le premier est l’archimédie. Les autres sont là pour aboutir à \(\mathbb{R}\) comme corps de nombres).
En anticipant un peu, signalons que les procédés de Dehn pour construire la géométrie non legendrienne, en supprimant une droite et ses points sont adaptés par Bachmann pour ses exemples de géométries semi elliptiques ou semi-hyperboliques.
Le propos de Bachmann est d’introduire de nouveaux axiomes pour retrouver les trois grands types de géométrie : elliptique, euclidienne et hyperbolique. Avant cette séparation, il prévient que cette démarche, tout algébrique, va nécessairement produire des généralisations qui peuvent être considérées par certains comme gênantes au moins en terme de représentation de l’euclidien puisque, sans axiome supplémentaire de continuité, il va exister une infinité de plans euclidiens non isomorphes, ce qui est une démarche très différente de celle de Hilbert qui cherchait – en particulier par l’introduction des axiomes d’intégrité – à retrouver le plan euclidien réel rapidement et de manière catégorique.
La géométrie elliptique
Le premier axiome de séparation des géométries est l’étude du cas de la polarité. La démarche portant sur le groupe de transformations initial, on peut l’exprimer sous la forme :
Axiome \(\mathbf{P}\) : Il existe un trilatère polaire (ie trois droites \(\mathbf{a, b, c}\) telles que \(\mathbf{abc=1}\))
Bachmann appelle groupe elliptique de transformations un groupe \(\Gamma\) vérifiant \(\mathbf{P}\), et plan elliptique le couple \((\Gamma, \Delta)\) quand \(\Gamma\) vérifie l’axiome de polarité. Nous choisirons, dans toute cette section, d’appeler le couple \((\Gamma, \Delta)\), muni des 5 axiomes de base, « plan de Bachmann », et donc, muni de l’axiome de polarité, nous parlerons de plan elliptique de Bachmann.
Nous avons vu (théorème 2) que l’existence de trois droites \(a, b, c\) telles que \(abc=1\) est équivalente au fait que ces trois droites sont deux à deux orthogonales (trilatère polaire) ou encore qu’un point est égal à une droite (de \(abc=1\), il vient \(a=bc=A\) puisque \(b \mid c\)) : il existe \(A\) tel que \(A=a\). L’existence d’un point égal à une droite, acquise comme un résultat équivalent à l’axiome de polarité \(\mathbf{P}\), le contexte axiomatique de Bachmann aboutit à ce résultat :
Théorème : Dans un groupe elliptique de transformations, tout point est égal à une droite et réciproquement.
D’un point de vue géométrique – dans le champ des configurations – cela signifie que chaque droite a un pôle et chaque point une polaire.
Pour montrer ce résultat, Bachmann commence par un lemme (indépendant de l’axiome de polarité) :
Lemme sur la polarité : si \(A \mid b\) alors \((\exists a \; / \; a=A) \; \Leftrightarrow \; (\exists B \; / \; B=b)\)
Preuve du lemme : De \(A \mid b\) on peut poser \(c=Ab\), et donc \(b=Ac\) et \(A=bc\). Autrement dit \(A \mid c\) et \(b \mid c\)
(plus simplement, on considère la perpendiculaire à \(b\) en \(A\) – dont on sait qu’elle est unique – d’où ces relations).
Sens direct : S’il existe \(A\) tel que \(A=a\), alors \(b=ac\) avec \(a \mid c\) et donc il existe \(B=ac\) tel que \(B=b\).
Réciproquement, s’il existe \(B\) tel que \(B=b\), alors \(A=Bc\) avec \(B \mid c\) donc \(Bc\) est une droite \(a\), et donc il existe \(a\) tel que \(a=A\).
Preuve du théorème : On suppose donc qu’il existe un point \(A\) et une droite \(a\) telle que \(A=a\). Soit alors \(g\) une droite quelconque. Montrons que \(g\) est un point. Considérons \(U\) un point de \(g\) ( c’est-à-dire \(U \mid g\) et donc \(U \neq g\)). Soit alors \(h\) l’unique droite incidente à \(U\) et \(A\) (existence et unicité par les axiomes A1 et A2). On applique trois fois le lemme précédent :
•De \(A \mid h\) et \(A=a\), on déduit du lemme qu’il existe un point \(H\) tel que \(H=h\).
• De \(U \mid h\) et \(H=h\), il en résulte alors que \(U\) est une droite ; il existe \(u\) telle que \(u=U\).
• Enfin de \(U \mid g\) et \(U=u\), il en résulte qu’il existe \(G\) tel que \(G=g\)
On montrerait de même que pour tout point \(G\) quelconque, il existe une droite \(g\) telle que \(G=h\).
Conséquences du théorème
Remarquons déjà que si \(A=a\), les propriétés \(g \mid A\) et \(g \mid a\) sont équivalentes, ce qui signifie que toute droite orthogonale à une droite passe par son pôle et réciproquement toute droite passant par le pôle d’une droite lui est orthogonale.
Cette polarité donne à la géométrie elliptique non seulement une structure projective d’incidence, mais plus encore, comme nous venons de le voir, par la dualité entre l’incidente et l’orthogonalité. Précisons un peu plus cela, simplement en réinterprétant les deux axiomes d’incidence qui peuvent se résumer par cette propriété :
Axiomes A1 et A2 : Étant donné deux points \(A\) et \(B\) distincts, il existe une unique droite \(d\) telle que \(A, B \mid d\).
Dual 1 : (en échangeant droites et points: \(a=A, b= B\) et \(D=d\))
Par deux droites distinctes, il passe un et un seul point.
Ainsi en géométrie elliptique deux droites distinctes sont toujours sécantes. Et en particulier, il n’existe qu’un type de pinceau, les pinceaux à centre.
Dual 2 : (en échangeant seulement les deux premières droites : \(a=A, b= B\))
Deux droites distinctes ont toujours une et une seule perpendiculaire commune.
En particulier cette unique perpendiculaire commune est la polaire de leur intersection. Et donc tous les pinceaux à centre sont aussi pinceaux à axe (et les équidistantes des cercles).
Dual 3 : (en conservant \(A\), échangeant \(B=b\) avec \(b \neq A\)) Par un point donné et une droite non polaire de ce point, il passe une et une seule droite orthogonale à la droite en ce point.
C’est aussi, en géométrie absolue, les théorèmes 3 et 4. Dans le cas elliptique, ces théorèmes sont simplement une autre lecture des axiomes. Cet exemple illustre, combien des résultats parfois délicats à montrer dans le cadre général de la géométrie absolue, s’obtiennent bien plus facilement dans les géométries particulières avec leurs outils propres. C’est en particulier le cas du pinceau des médianes – encore non abordé dans ces pages. Nous avons l’exemple ici d’un résultat toujours présent dans les preuves, un peu subtil à obtenir en début de la théorie, mais qui est une conséquence triviale dans un cadre plus précis.
Il découle immédiatement de la dualité que, de \(A \neq B\) et par \(a=A, b= B\), on peut écrire \(a \perp b \; \Leftrightarrow \; A \mid B\). Autrement dit \(AB\) est d’ordre 2 :
Les pôles de deux droites orthogonales sont mutuellement milieux l’un de l’autre : le produit \(AB\) étant involutif, on a \(ABA=B\) et \(BAB=A\) : \(A\) est milieu de \((B, B)\) et \(B\) milieu de \((A, A)\).
D’un point de vue géométrique, c’est une façon de dire que la symétrie centrale de centre \(A\) admet comme point invariant, non seulement son centre \(A\) mais tous les points de la polaire de \(A\). Il en résulte en particulier, que la polaire \(a\) de \(A\), au sens que l’on en a donné(*) avec les symétries est aussi un cercle de centre \(A\) et, dans ce cas particulier, le cercle \(a\) est invariant point par point dans la symétrie de centre \(A\).
(*) Bien entendu,, ce n’est pas encore abordé dans notre développement linéaire de l’axiomatique de Bachmann, mais dans cette page du menu DP, on a défini un cycle comme l’image d’un point par un pinceau. Ce cycle s’appelle un cercle si le pinceau est à centre, une équidistante s’il est à axe, et un horicycle s’il est dans support.
Dans le cas où \(A\) et \(B\) ne sont pas sur les polaires l’un de l’autre, alors l’existence d’un milieu \(I\) de \((A, B)\) montre que l’intersection \(J\) de la droite \((AB)\) et de la polaire de \(I\) est un autre milieu de \((A, B)\) : dans le cas général de deux points \(A\) et \(B\) tels que \(AB\) ne soit pas involutif, l’existence(*) d’un milieu de deux points assure l’existence d’un second milieu.
(*) Dans un contexte général où l’on ne dispose pas d’axiomes supplémentaires, l’existence du milieu de deux points (équivalente à celle d’une médiatrice) n’est pas une conséquence des premiers axiomes car la géométrie de Bachmann n’est pas a priori homogène. Pour cela il faudrait que le groupe soit transitif. Nous en verrons une équivalence en terme de corps dans une future page sur les corps associés.
Enfin signalons que, par le théorème 4, dans un plan non elliptique, l’unicité de la perpendiculaire à une droite issue d’un point est toujours vérifiée, ce qui va tout de suite être utile dans l’introduction du second axiome de distinction des géométries.
La géométrie euclidienne
On introduit désormais un nouvel axiome, que nous choisissons d’appeler simplement l’axiome du rectangle, même si Bachmann est bien plus précis dans son vocabulaire : il parle de rectilatère. Chacun comprendra qu’il a bien raison de ne pas utiliser, même dans un mot construit, une quelconque référence, fut-elle indirecte, au concept d’angle. On comprendra aussi que, pour une fois, parce qu’il n’y a pas d’ambiguïté, nous avons choisi de ne pas le suivre.
Axiome \(\mathbf{R}\) : Il existe quatre droites \(\mathbf{a, b,c, d} \; \mathbf{(a} \neq \mathbf{b, c} \neq \mathbf{d)}\) telles que \(\mathbf{a, b} \mid \mathbf{c,d}\)
Autrement dit il existe deux droites distinctes qui ont (au moins) deux perpendiculaires communes. Nous avons vu que l’axiome de polarité entraînait l’unicité de la perpendiculaire commune de deux droites distinctes.
On a \(\mathbf{P} \Rightarrow \neg \mathbf{R}\), et donc \(\mathbf{R} \Rightarrow \neg \mathbf{P}\). Avec l’axiome du rectangle nous sommes dans un plan non elliptique, et en particulier nous disposons de l’unicité de la perpendiculaire à une droite issue d’un point.
Retrouver la géométrie euclidienne, dans ce contexte, c’est retrouver l’unicité de la non sécante à une droite passant par un point donné. Or nous n’avons que des résultats sur l’orthogonalité. Pour voir le lien entre les deux, Bachmann introduit ce nouveau concept :
Equi-perpendicularité
Deux droites seront dites équi-perpendiculaires si les pinceaux de leurs perpendiculaires coïncident, autrement dit si toute perpendiculaire à l’une est perpendiculaire à l’autre.
Tout d’abord, deux droites équi-perpendiculaires sont nécessairement non sécantes : si \(I\) est l’intersection de deux telles droites \(a\) et \(b\), la perpendiculaire \(d\) à \(I\) en \(a\) admet deux perpendiculaires en \(I\) : \(a\) et \(b\), ce qui est contradictoire avec \(\neg \mathbf{P}\).
Ensuite les propriétés des pinceaux à axe (Th 7 et Th 9) montrent que si deux droites ont deux perpendiculaires communes, elles sont équi-perpendiculaires. On peut alors utiliser cette propriété (dite « PCEqui » dans la suite) pour montrer les équivalences suivantes :
Théorème du rectangle et théorème des trois points
Théorème : dans un groupe de transformations de Bachmann, les propriétés suivantes sont équivalentes :
- a) L’axiome du rectangle : Il existe quatre droites \(a, b, c, d\) telles que \(a, b \mid c, d\) (avec \(a \neq b\) et \(c \neq d\)).
- b) Le théorème des trois points : Un produit de trois points est toujours un point.
- c) Le théorème du rectangle : Si un quadrangle a trois angles droits, le quatrième est droit. Ou encore en langage moins géométrique, et dans la formulation de Bachmann : si \(a \perp c,d\) et \(b \perp c\) alors \(b \perp d\).
Le théorème des trois points va être essentiel pour la structure qui va suivre. Remarquons que l’équivalence entre l’axiome du rectangle et le théorème du rectangle signifie, compte tenu de ce que l’on sait sur l’orthogonalité, que deux droites sont équi-perpendiculaires dès qu’elles ont une perpendiculaire commune.
Preuve du théorème
\(\mathbf{a} \Rightarrow \mathbf{b}\)
Soient \(g, h\) et \(g_1, h_1\) les 4 droites de l’axiome du rectangle \((g, h \mid g_1 h_1)\). Montrons un premier lemme :
Pour toutes droites \(x\) et \(x_1\) telles que \(x \perp g_1\) et \(x_1 \perp g\) alors \(x \perp x_1\).
En effet, \(g_1\) et \(h_1\) étant équi-perpendiculaires (PCEqui), il vient \(g, x \perp g_1, x_1\) et donc, toujours par PCEqui, \(g\) et \(x\) sont aussi équi-perpendiculaires.
Soient alors \(A, B, C\) trois points. Notons \(a, b, c\) les perpendiculaires à \(g_1\) issues de \(A, B, C\) et \(a_1, b_1, c_1\) celles perpendiculaires à \(g\), issues des mêmes points.
Par l’application du lemme précédent, il vient \(a, b, c, g, h \perp a_1, b_1, c_1, g_1, h_1\). Il en résulte que les droites \(a, b, c\) et les droites \(a_1, b_1, c_1\) commutent, mais aussi (par le théorème 1) que \(A=aa_1, B=bb_1\) et \(C=cc_1\).
Par ailleurs \(abc\) et \(a_1b_1c_1\) sont des droites \(d\) et \(d_1\) telles que \(d \perp g_1\) et \(d_1 \perp g\), et toujours par le lemme précédent \(d \perp d_1\) de telle sorte que \(dd_1=D\) est un point.
La commutativité signalée ci-dessus permet de conclure car \(ABC = aa_1.bb_1.cc_1 = abc.a_1b_1c_1=dd_1=D\).
\(\mathbf{b} \Rightarrow \mathbf{c}\)
On suppose que le produit de trois points est un point. Soit alors \(a, b\) et \(c, d\) telles que \(a, b \perp c\) et \(a \perp d\).
Notons \(B:bc, \; C=ca\) et \(D=ad\).
Alors \(BCD=bc.ca.ad=bd\) est un point par hypothèse, c’est-à-dire que \(b \perp d\).
\(\mathbf{c} \Rightarrow \mathbf{a}\)
Il suffit de montrer que les hypothèses du théorème du rectangle peuvent être vérifiées. Or on sait qu’une droite contient au moins trois points, et qu’il y a toujours une perpendiculaire à une droite issue d’un point de cette droite. Les hypothèses du théorème sont toujours vérifiées, et donc il existe alors deux paires de droites deux à deux orthogonales, c’est bien l’axiome du rectangle.
Connectabilité
Le théorème du rectangle montre qu’un plan de Bachmann qui vérifie l’axiome \(\mathbf{R}\) a des propriétés proches de celles attendues. Par exemple, de ce qui précède, il est immédiat que :
Par un point non incident à une droite il passe une et une seule équi-perpendiculaire à cette droite.
Ce serait l’axiome d’Euclide si on savait que les seules droites non sécantes à une droite donnée sont ses équi-perpendiculaires, c’est-à-dire les droites ayant une perpendiculaire commune avec elle. Mais on sait, par le rappel historique sur la classification de Dehn qu’il n’en est rien. Il existe des plans semi-euclidiens, qui vérifient l’axiome \(\mathbf{R}\), et pour lesquels par un point il peut passer (éventuellement) une infinité de non sécantes à une droite donnée.
Pour séparer cette géométrie semi-euclidienne (dans laquelle la propriété précédente montre que l’équi-perpendicularité joue le même rôle que le parallélisme euclidien) de la géométrie euclidienne, il suffit d’exclure cette possibilité, en n’offrant pas d’alternative entre les droites sécantes et les droites équi-perpendiculaires.
C’est donc ce que propose Bachmann en introduisant une nouvelle définition :
Deux droites sont dites connectables si elles ont soit un point soit une perpendiculaire en commun. D’où l’axiome de connexion :
Axiome \(\mathbf{C}\) : deux droites sont toujours connectables.
Un plan métrique qui vérifie les axiomes \(\mathbf{R}\) et \(\mathbf{C}\) est dit un plan euclidien. Et dans ce cas, si on appelle parallèles deux droites non sécantes, il y a équivalence entre l’équi-perpendicularité et le parallélisme.
Le milieu de deux points
Dans un plan euclidien(*), le théorème des trois points a de nombreuses conséquences. Une première, triviale, mais systématiquement utile, est que, le produit de trois points étant un point, il est involutif, soit \(ABC=CBA\) (toujours utilisé dans les preuves suivantes).
(*) En pratique, sauf mention contraire, les propriétés suivantes sont vraies dans un plan muni seulement de l’axiome \(\mathbf{R}\), donc dans la géométrie semi-euclidienne. Bien-sûr, il faut remplacer l’expression « parallèles » par « équi-perpendiculaires », et alors même les propriétés des parallèlogrammes sont vraies (elles sont semi-euclidiennes)
Lemme (vrai dans \(\neg \; \mathbf{P}\)) : si \(A\) et \(B\) sont deux points distincts, alors \(AB \neq BA\).
En effet soit \(d\) l’unique droite incidente à \(A\) et \(B\), alors il existe \(a\) et \(b\) telles que \(A=ad=da\) et \(B=bd=db\), et \(a \neq b\). Alors \(AB=ab\) et \(BA=ba\).
Si \(AB=BA\) alors \(b^a=b\) et \(b\) est invariante dans la symétrie par rapport à \(a\), les deux droites, distinctes, ne peuvent qu’être orthogonales. C’est impossible, dans un cas non elliptique, car \(a\) et \(b\) sont en pinceau à axe, d’axe \(d\) et, dans \(\neg \; \mathbf{P}\), un pinceau à axe n’est jamais un pinceau à centre.
Par contraposée (vrai dans \(\neg \; \mathbf{P}\)) : si \(AB=BA\), alors \(A=B\).
Conséquence : unicité du milieu de deux points (en utilisant le théorème des trois points)
On suppose qu’il existe un point \(I\) tel que \(A^I=B\) (\(I\) est dit milieu de \(A\) et \(B\) car \(B^I=A\)). On a donc \(AI=IB\). Soit \(J\) un autre milieu de \(A\) et \(B\) : \(AJ=JB\). On a donc \(I=AIB=BIA\) et \(J=AJB=BJA\). Il en résulte que \(IJ=AIB.BJA=AIJA\) soit \(AIJ=IJA=AJI\). D’où\(IJ=JI\) soit, par le lemme précédent, \(I=J\).
Les parallélogrammes : propriété des milieux
Soit alors deux points \(A\) et \(C\) tel que le milieu \(I\) existe. On a donc \(AI=IC\). Alors pour tout point \(B\), le produit \(ABC\) est un point \(D\) et on peut écrire \(DI=ABC.I = CBA.I = CB.AI= CB.IC = CBI.C=IBC/C=IB\). Ainsi le milieu de \((A, C)\) est aussi milieu de \((B, D)\) où \(D=ABC\).
On appelle parallélogramme \(ABCD\), 4 points \(A, B, C, D\) tels que \(D=ABC\). Alors si l’un des couples \((A, C)\) ou \((B, D)\) a un milieu c’est aussi celui de l’autre.
Parallélogrammes : caractérisation par les translations
Le produit de deux points \(AB\) est appelé une translation. Avec les notations du lemme, on a \(AB=ab\), indépendamment de la structure euclidienne(*). Mais dans le cas euclidien, en se fixant un point \(P\) , chaque translation \(AB\) peut se représenter par \(AB=PQ=pq\) (avec des notations évidentes) où \(Q\) est le point donné par \(Q=PAB\). On a donc \(ab=pq\), ce qui signifie, compte tenu des propriétés vues sur les pinceaux (sachant que \(abq=p\) est une droite) que les quatre droites appartiennent au même pinceau à axe \(\mathscr{P}_{ab}\). Il en résulte que \((AB)\), axe de\(\mathscr{P}_{ab}\) et \((PQ)\), axe de \(\mathscr{P}_{pq}\) sont équi-perpendiculaires, c’est-à-dire parallèles. De même pour \((AP)\) et \((BQ)\). D’où le nom de parallélogramme.
(*) D’une manière générale, en géométrie absolue les translations existent et ont les mêmes propriétés élémentaires qu’ici, mais seulement sur la perpendiculaire commune à \(a\) et \(b\). En géométrie absolue la translation \(AB\) n’a de sens que sur la droite \((AB)\), et ne s’étend au plan que quand on dispose du théorème des trois points.
Soit \(D\) le point tel que \(ABC = D\) alors \((AB) \; // \; (CD)\) et \((AD) \; // (\; BC)\).
Réciproquement soient quatre points \(ABCD\) sont tels que \((AB) \; // \; (CD)\) et \((AD) \; // \; (BC)\).. Soit alors \(D’=ABC\). Alors \(ABCD’\) est un parallélogramme. Et par unicité de la parallèle(*) à \((BC)\) issue de \(A\) et à \((AB)\) issue de \(C\), il vient \(D=D’\), ce qui achève l’équivalence entre la caractérisation par les côtés et la définition par les produits.
(*) Si on conserve le vocabulaire d’équi-perpendiculaire, on voit que tous ces résultats sont vrais dans les plans semi-euclidiens : on n’utilise que le théorème des trois points, équivalent à l’axiome \(\mathbf{R}\) et sa conséquence sur l’unicité d’une équi-perpendiculaire à une droite donnée passant par un point donné.
Ce résultat conduit à deux conséquences immédiates : tout d’abord si \(ABCD\) est un parallélogramme (\(D=ABC\)), alors les translations \(AB\) et \(DC\) sont égales, ainsi que \(AD\) et \(BC\). La réciproque est immédiate, d’où la caractérisation par les translations
\(ABCD\) est un parallélogramme si et seulement si \(AB=DC\)
Une seconde conséquence porte sur les symétries centrales : l’image d’une droite est une droite parallèle (ou équi-perpendiculaire). Dans le cas absolu général, l’image d’une droite est une droite qui a une perpendiculaire commune avec la première, mais c’est sans intérêt sans l’axiome \(\mathbf{R}\) qui donne un autre sens à la perpendiculaire commune.
Si deux droites \(m\) et \(n\) ont une perpendiculaire commune, le produit \(mn\) est une translation. Il suffit de prendre \(M\) incident à \(m\) et \(N\) l’intersection de \(n\) et de sa perpendiculaire issue de \(M\). D’après ce qui précède, \(mn=MN\), ceci pour tout point \(M\) de \(m\).
Par ailleurs, \(AA\) est la translation \(Id\). Et dans ce cas \(AA\) peut toujours s’écrire \(aa\), produit de deux droites équi-perpendiculaires confondues (quelconques).
Le groupe des translations
Par le théorème des trois points, le produit de deux translations, produit de 4 points s’écrit aussi comme produit de deux points ce qui signifie que le produit de deux translations est une translation. Il est facile alors de vérifier que les translations forment un sous-groupe \(\mathscr{T}\).
De plus \(\mathscr{T}\) est commutatif. En effet, \(PQ.P’Q’ = PQP’.Q’=P’QP.Q’=P’.QPQ’=P’.Q’PQ=P’Q’.PQ\). Il y a bien commutativité du groupe des translations \(\mathscr{T}\).
Par ailleurs la relation générale \((AB)^{\alpha} = A^{\alpha}B^{\alpha}\) montre que \(\mathscr{T}\) est un sous-groupe distingué du groupe euclidien des transformations.
Structure du groupe euclidien de Bachmann
Notons pour un point \(O\) donné, \(\Gamma_O\) le sous-groupe des éléments de \(\Gamma\) qui laissent \(O\) invariant. Il contient les droites incidentes à \(O\) et les produits de deux telles droites (rotations de centre \(O\)). Par les théorèmes des tri-réflexions sur le pinceau à centre \(\mathscr{P}_O\), il est clair que ce sont les seules transformations de \(\Gamma_O\).
Théorème (décomposition des transformations euclidiennes planes)
Soit \(O\) un point arbitraire de \(\Gamma\), alors \(\Gamma=\Gamma_O.\mathscr{T}\). Plus précisément, toute transformation \(\alpha\)de \(\Gamma\) peut s’écrire de manière unique \(\alpha=\rho_O \tau\) avec \(\rho_O \in \Gamma_O\) et \(\tau \in \mathscr{T}\).
Preuve du théorème
Soit \(\mathscr{H} = \{ \rho_O \tau , \rho_O \in \Gamma_O , \tau \in \mathscr{T} \}\). L’existence de la décomposition revient à montrer que toutes les droites sont éléments de \(\mathscr{H}\) et que \(\mathscr{H}\) est stable par multiplication. L’unicité sera acquise en montrant que \(\Gamma_O \cap \mathscr{H} = \{Id\}\).
i) Les droites sont dans \(\mathscr{H}\). Soit \(d\) une droite et \(d_O\) l’équi-perpendiculaire à \(d\) passant par \(O\). (on peut dire parallèle, mais nous n’utilisons pas l’axiome \(\mathbf{C}\)). Alors \(d=d_Od_Od\). Et nous avons vu que \(d_Od\) est une translation.
ii) \(\mathscr{H}\) est stable par multiplication. \(\rho_1 \tau_1 . \rho_2 \tau_2 = \rho_1 \rho_2 (\rho_2)^{-1} \tau_1 \rho_2 \tau_2 = \rho_1 \rho_2 \tau_1 ^{\rho_2}\tau_2\) qui est un élément de \(\mathscr{H}\) car \(\Gamma_O\) est un sous-groupe, et \(\mathscr{T}\) est un sous-groupe distingué.
Comme les droites engendrent \(\Gamma\), les deux propriétés précédentes montrent que \(\mathscr{H} = \Gamma\)
iii) \(\Gamma_O \cap \mathscr{H} = \{Id\}\). Soit \(\tau\) un élément de \(\Gamma_O \cap \mathscr{H}\). On peut écrire \(\tau=ab\) le produit de deux droites équi-perpendiculaires.
D’autre part puisque \(\tau \in \Gamma_O\), il y a deux possibilités : soit \(\tau=g\) avec \(g \mid O\) soit \(\tau=gh\) avec \(g, h \mid O\).
Le cas \(ab=g\). Alors \(a \mid b\) et donc \(ab\) serait un point \(G\), soit \(G=g\) ce qui est exclu car avec l’axiome du rectangle, nous sommes dans le contexte \(\neg \mathbf{P}\).
Le cas \(ab=gh\). Si \(g=h\), alors \(a=b\) et \(\tau=Id\), ce que l’on voulait montrer.
Sinon, on peut écrire \(a=ghb\), soit \(b \in \mathscr{P}_{gh}\) et, par les Th 8 puis Th 4, il vient \(a,b \mid O\). Comme \(a\) et \(b\) sont équi-perpendiculaires, avoir un point commun signifie être confondues. Donc dans ce cas, on a encore \(a=b\) et \(\tau=Id\).
L’unicité de l’écriture découle de iii) par les arguments usuels sur les structures de groupe.
La géométrie hyperbolique
On se place désormais dans \(\neg \; \mathbf{C}\) :
Axiome \(\neg \; \mathbf{C}\) : il existe des droites qui n’ont ni point ni perpendiculaire en commun.
Autrement dit : il existe des droites non connectables.
Nous sommes alors dans une situation différente du cas euclidien (\(\mathbf{R}\) et \(\mathbf{C}\)), et du cas elliptique (qui vérifie \(\mathbf{C}\) car \(\mathbf{P} \Rightarrow \mathbf{C}\)). Mais \(\neg \; \mathbf{C}\) seul ne sépare pas d’avec ce qui précède (le cas semi-euclidien est \(\mathbf{R}\) et \(\neg \; \mathbf{C}\)).
Soient \(a\) et \(b\) deux droites non connectables, \(\mathscr{P}_{ab}\) est sans support (pas de centre, pas d’axe). Donc dans le cadre \(\neg \; \mathbf{C}\), il existe des pinceaux sans support alors que d’une manière générale, dans la géométrie absolue leur existence est seulement non exclue. Par les différents théorèmes sur les pinceaux, deux droites d’un pinceau sans support sont toujours non connectables. Mais on n’a pas d’informations supplémentaires. En particulier, nous verrons , dans un futur article de blog, que sans plus de précision, les pinceaux sans supports peuvent être bien plus généraux que le cas hyperbolique usuel, et même entre eux, de natures différentes.
Pour retrouver la géométrie hyperbolique, il faut bien entendu restreindre tous ces possibles.
Considérons une droite \(g\) passant par \(P\) et non connectable à une droite \(h\), et notons \(u\) la perpendiculaire à \(h\) issue de \(P\). Alors la droite \(g^u\) (notée \(gu\) ci-contre), symétrique de \(g\) par rapport à la droite \(u\), est elle aussi non connectable à \(h\).
Mais rien n’interdit, en général qu’il y ait d’autres droites que \(g\) et \(g^u\) passant par \(P\) non connectables à \(h\). Or en géométrie hyperbolique, il n’y en a que deux.
D’où la mise en place d’un nouvel axiome :
Axiome \(\mathbf{H}\) : Si \(\mathbf{P} \mid \mathbf{a, b, c} \) et les couples \(\mathbf{(a, g), (b, g), (c, g)}\) sont des couples de droites non connectables, alors, soit \(\mathbf{a=b}\), soit \(\mathbf{b=c}\), soit \(\mathbf{a=c}\).
Étant donnés un point \(P\) et une droite \(g\), il passe par \(P\) au plus deux droites non connectables avec \(g\).
Un plan hyperbolique est alors un plan qui vérifie les axiomes \(\neg \; \mathbf{C}\) et \(\mathbf{H}\). Il convient alors de vérifier que les géométries ainsi définies sont bien distinctes les unes des autres.
Pour cela, Bachmann montre que \((\neg \; \mathbf{C}\) et \(\mathbf{H}) \Rightarrow \neg \; \mathbf{R}\).
En pratique, il est équivalent de montrer que \((\neg \; \mathbf{C}\) et \(\mathbf{R}) \Rightarrow \neg \; \mathbf{H}\), et utiliser l’axiome du rectangle autorise une certaine souplesse par l’utilisation de l’équi-perpendicularité et des translations. En particulier, on utilise le lemme technique suivant :
Lemme : Avec l’axiome \(\mathbf{R}\), si \(u\) et \(v\) sont équi-perpendiculaires alors pour une droite \(a\) quelconque, \(a^u\) et \(a^v\) aussi.
Preuve du lemme : L’équi-perpendicularité de deux droites \(u\) et \(v\) est équivalente au fait que \(uv\) soit une translation. Et avec l’axiome \(\mathbf{R}\), les translations forment un groupe distingué.
Donc si \(uv\) est une translation, \((uv)^a\) aussi et on a \(a^ua^v=[(uv)^a(vu)]^u\). Donc \(u^av^a\) est une translation, c’est-à-dire que les droites sont équi-perpendiculaires, ce qui, sous \(\mathbf{R}\), signifie aussi qu’elles ont une perpendiculaire commune et donc qu’elles sont dans un faisceau à axe.
Preuve de l’implication \((\neg \; \mathbf{C}\) et \(\mathbf{R}) \Rightarrow \neg \; \mathbf{H}\).
Soient deux droites non connectables \(a\) et \(g\) (par \(\neg \, \mathbf{C}\)) et \(P\) et \(Q\) deux points de \(a\) (il existe au moins trois points). Notons \(u\) et \(v\) les perpendiculaires à \(g\) issues de \(P\) et \(Q\).
Comme indiqué dans l’introduction à l’axiome \(\mathbf{H}\), par symétrie par rapport à \(v\), les droites \(a^v\) et \(g\) sont non connectables. En particulier \(a\), \(a^v\) (incidentes à \(Q\)) ne sont pas en pinceau avec \(g\). De même \(a^u\) et \(g\) ne sont pas connectables. Par ailleurs, puisque \(a^v\) et \(a^u\) sont en pinceau à axe, \(a^u, a^v\) et \(g\) ne sont pas en pinceau. De même puisque \(a\) et \(a^u\) sont incidentes en \(P\), les droites \(a\), \(a^u\) et \(g\) ne sont pas en pinceau.
Soit maintenant \(c\) la droite incidente à \(P\) appartenant au pinceau \( \mathscr{P}_{a^vg}\) – dont l’existence est une conséquence de Hjelmslev – alors \(c\) est non connectable à \(c\). Or elle est différente de \(a\) (car \(a, a^v, c\) non en pinceau) et différente de \(a^u\) (car \(a^u, a^v, g\) non en pinceau).
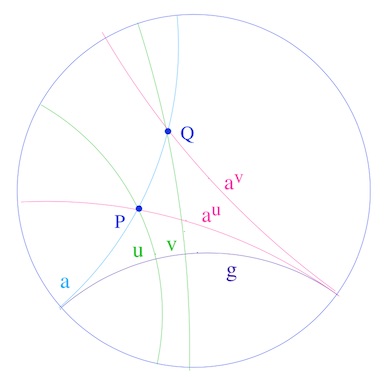
Donc \(\mathbf{R}\) et \(\neg \; \mathbf{C}\) conduit à ce que \(P\) soit incident à trois droites non connectables à \(g\), ce qui est contraire à \(\mathbf{H}\). Ainsi la géométrie hyperbolique est bien distincte des géométries semi-euclidiennes.
Dans le cas hyperbolique (ci-contre avec le disque de Poincaré), il est clair au contraire que \(a^u\), et \(a^v\), sont en pinceau avec \(g\), et certainement pas en pinceau à axe, comme quand on est sous l’axiome du rectangle.
Le plus remarquable est que cet axiome évacue toutes les autres possibilités de pinceaux sans support en les réduisant d’un coup, avec un vocabulaire projectif, au cas minimal des seules intersections d’une droite avec la conique absolue de Cayley (dans un contexte géométrique suffisamment riche pour que ces objets existent – ci dessus les points idéaux du cercle horizon). Ce résultat est assez troublant quant aux potentialités structurelles des plans métriques, somme toute, en définitive, relativement limitées.
Caractérisation de la géométrie hyperbolique par les bouts de la figure de Bergau
Cet axiome \(\mathbf{H}\) va permettre de fixer un vocabulaire spécifiquement hyperbolique aux faisceaux sans support. On dira tout d’abord que deux droites non connectables – qui définissent donc un faisceau – ont un même bout.
Puis on appellera bout(*), le pinceau sans support défini par deux droites non connectables. Alors l’axiome \(\mathbf{H}\) permet de dire que si une droite \(a\) un bout, elle en a toujours un second (et pas plus). En terme de représentation dans un modèle (comme DP ou KB), on aura compris qu’un bout \(M= \mathscr{P}_{ab}\) où \(a\) et \(b\) sont non connectables peut se représenter par un point idéal \(M\) sur le cercle horizon.
(*) Le terme bout a déjà été utilisé par Hilbert [extrémité dans la traduction de P. Rossier] dans son article de 1904 sur une construction de la géométrie hyperbolique n’utilisant pas la continuité : Hilbert reprend la méthode de Bolyai et définit les bouts à partir des demi-droites, utilisant explicitement une notion d’ordre. Voir l’article consacré à son (extraordinaire) corps des extrémités qui lui permet d’arriver à son objectif.
Bachmann montre ensuite deux propriétés élémentaires relatives à l’action des isométries sur les bouts des droites … qui en ont (car compte tenu de l’écriture de l’axiome \(\mathbf{H}\), on pourrait rencontrer des plans hyperboliques pour lesquels certaines droites n’auraient pas de bouts. Les modèles réels sont suffisamment riches pour que les droites aient toujours deux bouts).
1 – la symétrie orthogonale d’axe une perpendiculaire \(h\) à une droite \(d\) transforme un bout de \(d\) en l’autre.
2 – De même pour les symétries centrales de centre \(O\) appartenant à \(d\).
Ces propriétés des bouts étant spécifiques à la géométrie hyperbolique, Bachmann s’emploie ensuite à chercher, précisément, des caractérisations de la géométrie hyperbolique par des équivalents de l’axiome \(\mathbf{H}\). En particulier, il propose une figure caractéristique de la géométrie hyperbolique, comme le triangle polaire l’est de la géométrie elliptique et le rectangle de la géométrie (semi)-euclidienne. En pratique on a besoin de lier l’orthogonalité à ce qui fait la particularité hyperbolique : les pinceaux sans support et leurs propriétés.
Figure dynamique d’illustration de \((\neg \; \mathbf{C}\) et \(\mathbf{H}) \Rightarrow \neg \; \mathbf{R}\)
On construit un exemple où le produit de trois points est aussi le produit de deux droites sans support, donc certainement pas un point : on nie ainsi le théorème du rectangle équivalent à l’axiome du rectangle : si dessous on a \(A = gh, B = hu, C = uv\), avec \(v\) et \(g\) non connectables. Alors \(ABC=gv\) n’est pas un point.
Une figure qui motive l’étude des bouts.
Dans cette figure, on peut déplacer \(A\) et \(B\) ainsi que \(M\).
Rappel : quand on déplace des points, ceux des noms des droites vont sur le cercle horizon, on les déplace simplement à la souris.
Bien entendu, cette construction repose sur des propriétés du modèle (on utilise le point idéal \(M\) pour construire \(C\)), et dans le cadre général nécessite une justification.
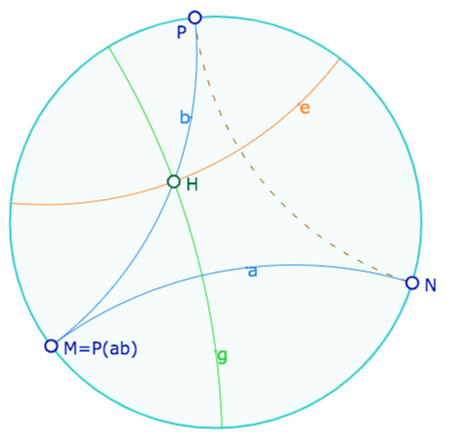
Lemme préliminaire à la figure de Bergau
Soient \(a\) et \(b\) deux droites non connectable. Notons \(M= \mathscr{P}_{ab}\) le bout associé, et \(N\) et \(P\) les deux autres bouts de \(a\) et \(b\). Soit \(g\) une perpendiculaire à \(a\) qui coupe \(b\) en \(H\) et \(e\) la perpendiculaire à \(g\) en \(H\). Alors latex]e[/latex] échange les bouts \(N\) et \(P\).
Preuve: On utilise les deux propriétés élémentaires précédentes des symétries axiales et centrales sur les bouts.
En effet, on a \(e=Hg\) et donc \(P^e = P^{Hg} = M^g = N\).
Ce lemme permet d’aborder une caractérisation des pinceaux hyperboliques non connectables.
Ci-dessous, \(a\) et \(b\) sont deux droites non connectables, \(g\) et \(d\) deux droites orthogonales à \(a\) telles que \(g\) rencontre \(b\) (en un point \(G\)). \(e\) est orthogonale à \(g\) en ce point et \(f\) est la perpendiculaire à \(b\) appartenant à \(\mathscr{P}_{de}\), donc \(def\) est une droite. Alors elle appartient à \(\mathscr{P}_{ab}\) :
Lemme des bouts de Bergau :
Soient i) \(g, d \mid a\), ii) \(b \mid ge\), iii) \(f \mid b\), iv) \(def \in \Delta\) . Alors : (\(\mathscr{P}_{ab}\) est un bout) \(\Rightarrow (def \in \mathscr{P}_{ab})\)
Les droites \(a\) et \(b\) sont pilotées par les poignées \(a_1, a_1, b_1, b_2\), le point \(b_2\) est aimanté par la droite non connectable à \(a\) – de bout \(M\) – passant par \(b_1\).
Les droites \(g\) et \(d\) sont pilotées par les poignées \(g_1, d_1\). Penser à rendre \(\mathscr{P}_{de}\) à axe en déplaçant \(d_1\)..
Attention, en déplaçant ces deux poignées, la droite \(f\) perpendiculaire à \(b\) et appartenant à \(\mathscr{P}_{de}\) peut ne pas exister … et alors \(def\) disparait.
Preuve : on reprend les notations de la figure précédente : \(M= \mathscr{P}_{ab}\), \(N\) et \(P\) les autres bouts de \(a\) et \(b\). Alors \(M^d=N, N^e=P\) ( par le lemme préliminaire) et \(P^f=M\) soit \(M^{def}=M\), autrement dit \(def \in \mathscr{P}_{ab}\).
Le lemme de Bergau – la figure associée(*) – est assez extraordinaire : dans la figure précédente, \(a\) et \(b\) ne sont pas a priori connectables : on peut déplacer la poignée \(b_2\) pour rendre les droites connectables ou pas. En manipulant ainsi la figure précédente, on s’aperçoit vite [on conjecture] que cette implication est en réalité une équivalence : la droite \(def\) n’appartient à \( \mathscr{P}_{ab}\) que si c’est un pinceau de droites non connectable : il s’agit donc d’une figure caractéristique de la géométrie hyperbolique.
Préférer ouvrir cette figure de caractérisation dans un nouvel onglet
Mais démontrer ce résultat est loin d’être trivial. Pour y arriver Bachmann commence par montrer deux conséquences du lemme de Bergau :
Théorème C1 : existence d’une perpendiculaire issue d’un bout
Soit \(M\) un bout et \(d\) une droite. Il existe une droite \(g \in M\) perpendiculaire à \(d\). (c’est la propriété utilisée pour faire la figure du lemme préliminaire)
Théorème C2 : joindre les deux bouts
Deux bouts quelconques ont toujours une droite en commun.
Ces deux théorèmes sont difficiles à obtenir : Bachmann utilise des outils non encore abordées dans ces pages (les demi-rotations de Hjelmselv). Ensuite, il montre que l’axiome \(\mathbf{H}\) (dans un contexte \(\neg \, \mathbf{C}\) sinon il n’y a rien à montrer) est équivalent, successivement au lemme de Bergau, au théorème C1 et au théorème C2. Pour obtenir ces équivalences (en fait les réciproques), il faut reformuler ces trois propriétés d’une manière plus générale, avec des droites, sans référence aux bouts, ce qui donne :
Bergau* : Soient \(a\) et \(b\) deux droites non connectables et \([a, b, g, d, e, f]\) les hypothèses du lemme de Bergau. On pose \(c=def\). Alors \(acb\) est une droite.
C1* : On suppose que \(a\) et \(b\) sont deux droites non connectables et que \(c\) est une droite telle que \(abc\) ne soit pas une droite. Alors il existe une droite \(u\) telle que \(abu\) est une droite et \(c \perp u\).
C2* : On suppose que \(a, b\) d’une part et \(c, d\) d’autre part sont des droites non connectables. Alors il existe une droite \(u\) telle que \(abu\) et \(cdu\) sont des droites.
C’est en montrant C2* \(\Rightarrow\) Bergau* que l’on montre l’équivalence dans Bergau.
(*) Bachmann parle de « la figure du lemme de Bergau ». (Aufbau de 1959 p. 222 puis p. 229 pour les équivalences). Peter Bergau a soutenu sa thèse sous la direction de Bachmann en 1953, sur ce thème précis de la caractérisation de la géométrie hyperbolique dans le cadre de cette axiomatique.
Classification des géométries
Les axiomes de séparation des principales géométries étant mis en place, il s’agit de proposer un classement. D’une manière générique, Bachmann appelle « métrique euclidien » un plan qui vérifie l’axiome des rectangles, et « métrique non euclidien » un plan qui ne le vérifie pas. La famille des métriques euclidiens se décline alors en deux sous ensembles : les plans euclidiens et les plans semi-euclidiens.
Parmi les plans non euclidiens, Bachmann sépare les géométries qui vérifient l’axiome de connexion de ceux qui ne le vérifient pas. Dans le premier cas on trouve les géométries elliptiques (si l’axiome de polarité est vrai) et celles qu’il appelle « semi-elliptiques » si l’axiome de polarité n’est pas vrai. En pratique cette géométrie se rencontre comme sous ensemble – en terme de groupe – du précédent : pour chaque couple \((A, a)\) d’un point et de sa polaire, on considère un ensemble – vérifiant les axiomes de Bachmann) où l’on n’a qu’un des deux éléments du couple, soit la polaire, soit le pôle, de sorte que l’axiome de polarité (par son équivalent : \(\exists A, \, \exists a \; / \; A=a)\)) ne soit jamais vrai.
Enfin, dans le cas où l’axiome de connexion n’est pas vérifié, on distingue les géométries hyperboliques par l’axiome \(\mathbf{H}\) de toutes les autres dites alors semi-hyperboliques. La géométrie non legendrienne de Dehn est un exemple de ces géométries.
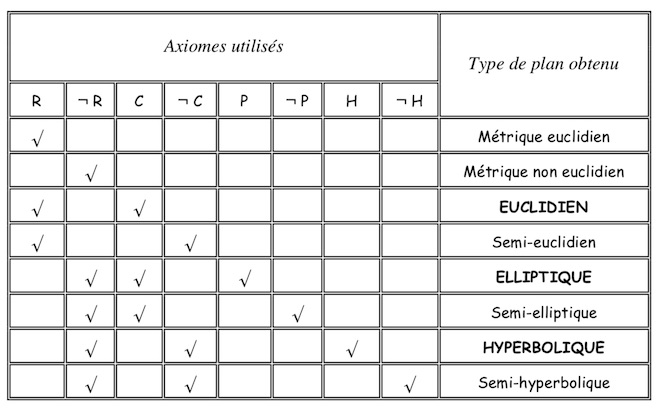
Dans son ouvrage Bachmann présente cette séparation des géométrie, après les chapitres consacrés à l’antiappariement et le plongement de sa géométrie dans un plan projectif, ce que nous avons choisi de développer après car peut intéresser moins de lecteurs (même s’il y a de très belles figures dans ces trois pages sur le plongement projectif). Il précise alors que, tout comme la géométrie euclidienne s’obtient en supprimant du plan projectif, la droite de l’infini et ses points, la géométrie semi-euclidienne correspond à la suppression de la droite de l’infini tout en conservant les points à l’infini.
Le plan idéal d’un plan métrique hyperbolique est toujours associé à un corps ordonné et les points du plan hyperbolique sont les points intérieurs à une conique fondamentale (d’où les modèles que nous utilisons, avec un cercle comme conique fondamentale).
Compléments
Il existe des plans métriques pour lesquels le corps associé au plan idéal n’est pas ordonnable. On peut même construire de tels plans euclidiens. On en présente un exemple dans cet article. Ce même article traite d’autres thèmes comme un plan qui relève de \(\neg \, \mathbf{R}\), \(\neg \, \mathbf{C}\) et \(\neg \, \mathbf{H}\) : c’est-à-dire un plan semi-hyperbolique qui a, de plus, la particularité de disposer de 4 types de pinceaux. On y explique aussi pourquoi les géométries de Bachmann finies sont nécessairement euclidiennes.