En dehors des points de l’ellipse, dont l’étude sera abordée dans une page dédiée, le modèle non arguésien de Hilbert est conforme. On peut rencontrer, a priori, deux types d’orthogonalité : le cas ordinaire euclidien, à l’extérieur de l’ellipse, et le cas d’arcs de cercle orthogonaux, à l’intérieur de l’ellipse.
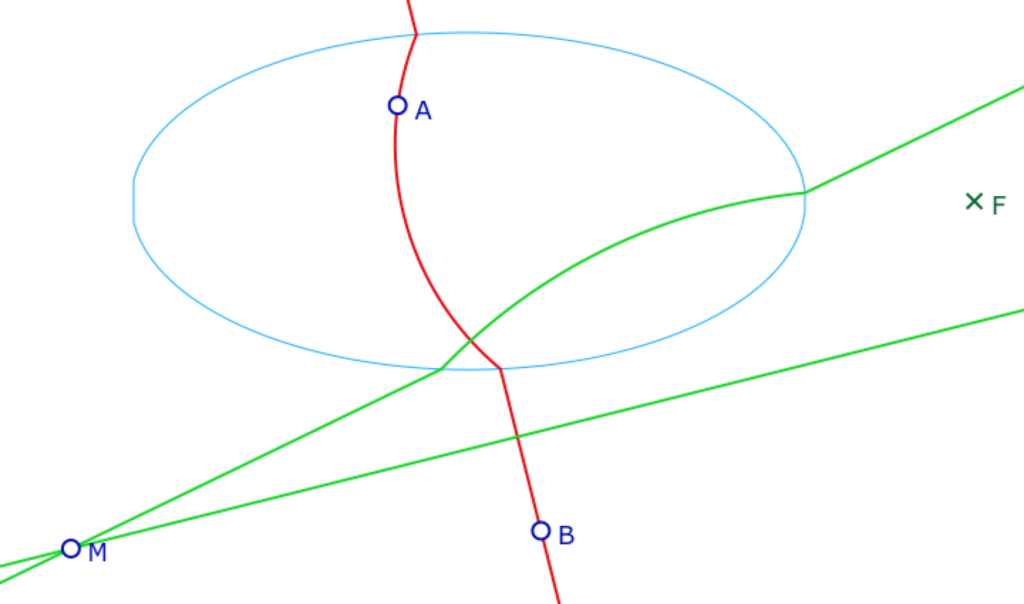
Il se peut alors, que, d’un point \(M\) du plan, on puisse même mener deux perpendiculaires à une droite \((AB)\) donnée comme ci-contre, une euclidienne et l’autre, que l’on dira hilbertienne, ou encore H-perpendiculaire.
Pour une droite euclidienne \(d\) (c’est-à-dire une H-droite qui ne coupe pas l’ellipse), de tout point du plan il existe toujours une et une seule perpendiculaire à cette droite, c’est la H-droite dont le support euclidien est la perpendiculaire à \(d\). On s’intéresse donc essentiellement dans la suite aux H-droites rencontrant l’ellipse. On imagine assez facilement qu’il puisse exister, dans certains cas à préciser, des régions du plan depuis lesquels on ne peut pas mener de perpendiculaire à une droite donnée.
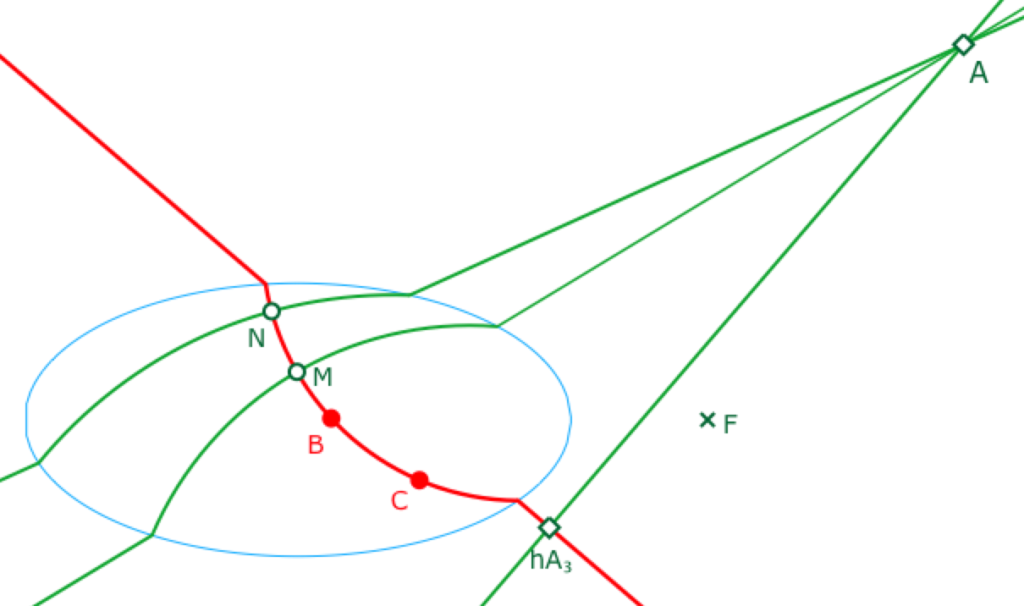
Quand nous avons étudié les rectangles à l’intérieur de l’ellipse, nous avons vu que si un quadrilatère a trois angles droits, il en a quatre, mais que les H-droites support ne sont généralement pas parallèles. Il en résulte qu’étant donné une droite coupant l’ellipse, il est facile de construire deux H-perpendiculaires à cette droite, sécantes entre elles. Et, dans certains cas, si ce point d’intersection peut être assez loin de l’ellipse, on peut rencontrer la situation ci-contre, où, par un point, il passe non pas deux, mais trois perpendiculaires à une droite donnée, deux hilbertiennes et une euclidienne.
Ci-contre, du point \(A\) il existe trois perpendiculaires à la droite \((BC)\).
L’orthogonalité est donc un thème très riche, et ce premier résultat, même s’il est élémentaire, est une spécificité du modèle de Hilbert. Par définition même du modèle, il n’y aura jamais trois perpendiculaires à une droite dans le modèle de Moulton. Ainsi les géométries non arguésiennes dans ces deux modèles ne sont pas identiques. Et ceci est sans rapport avec la définition de la congruence des angles dans le cas d’un sommet sur l’ellipse.
Manipulation d’une première perpendiculaire dynamique
On se donne une droite \((AB)\) et un point \(I\). On construit alors les perpendiculaires éventuelles à \((AB)\) issues de \(I\). La construction de ces perpendiculaires est précisée dans la dernière section de cet article consacré aux constructions algébriques des droites de Moulton.
On peut agir sur \(A, B\) et \(I\). Observer que dans certaines parties du plan,
il n’y a pas de perpendiculaires autres que l’euclidienne, et parfois pas du tout.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet
On notera qu’à l’ouverture de la figure, il y a trois perpendiculaires issues de \(I\) à la droite \((AB)\). Cela signifie qu’un des triangles de sommets \(I\) et deux des trois pieds des perpendiculaires a deux angles droits et même trois orthocentres alignés : les trois pieds des hauteurs, c’est donc un premier triangle tri-orthocentrique, même s’il est très particulier.
Illustration d’une situation très particulière
Dans la figure suivante, seulement en mode animation, non modifiable, une droite admet, pour quelques points \(K\), à la fois trois perpendiculaires hilbertiennes mais aussi une perpendiculaire euclidienne. Ainsi, pour quelques droites et une région très limitée des points on peut mener jusqu’à quatre perpendiculaires à une droite.
Figure animation – exceptionnellement non manipulable
On peut voir le déplacement de \(Ctr\) (et de la droite rouge), mais à peine celui de \(K\)
On notera que les triangles \(KhK_ihK_j\), pour \(i \neq j\) ou les triangles \(KhK_iHe\) sont tous quadri-orthocentriques d’orthocentres les 4 pieds des hauteurs … même si c’est un cas très particulier puisque les orthocentres sont alignés.
Préférer ouvrir cette figure dans un nouvel onglet
Les hauteurs d’un triangle
Puisqu’il peut y avoir, en général, deux hauteurs (rarement trois et plus encore quatre) issues d’un point, on a, possiblement jusqu’à six hauteurs dans un triangle (rarement 7 mais possible comme on le verra ci-dessous). Avec ces 6 hauteurs, on va trouver, assez facilement, des triangles orthocentriques de différents type, ou même, moins facilement, des triangles bi-orthocentriques.
Dans la figure suivante, à l’ouverture le triangle a 6 hauteurs dans une configuration très proche d’un triangle bi-orthocentrique.
Explorer les hauteurs d’un triangle en déplaçant les trois sommets.
On rappelle que les hauteurs sont concourantes quand les trois sommets et l’intersection sont toutes dans l’ellipse.
On revient à la condition initiale en rechargeant la figure avec l’icone de l’iframe (parfois il faut le faire 2 fois)
Préférer ouvrir cette figure (configuration plus grande) dans un nouvel onglet
Un premier triangle orthocentrique ayant 7 hauteurs
Juste pour le fun, comme sous produit des programmes présentés dans les pages suivantes, il est facile d’obtenir cette figure d’un triangle ayant 7 hauteurs dont trois concourantes.
Les deux hauteurs hilbertiennes issues de \(A\) et \(B\) se coupent en \(hABhh\). Celle issue de \(A\) et la hauteur issue de \(C\) se coupent en \(hAChe\). Un programme permet de déplacer très légèrement le point \(C\) afin de rendre nulle (au sens indiqué ci-dessous) la distance entre les deux points.
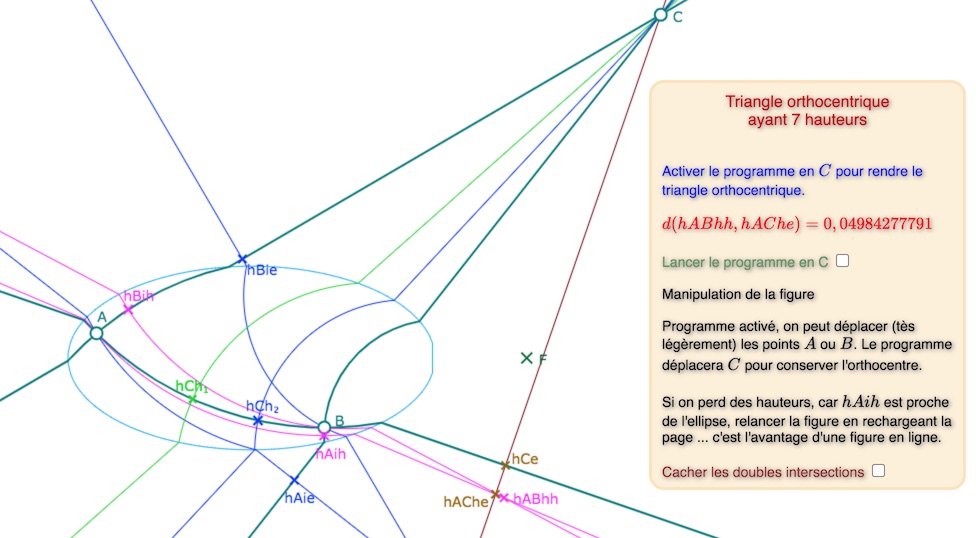
Il suffit de cocher la case pour que le triangle devienne orthocentrique (attention, ici ce n’est qu’une copie d’écran)
Lancer cette figure dans un nouvel onglet.
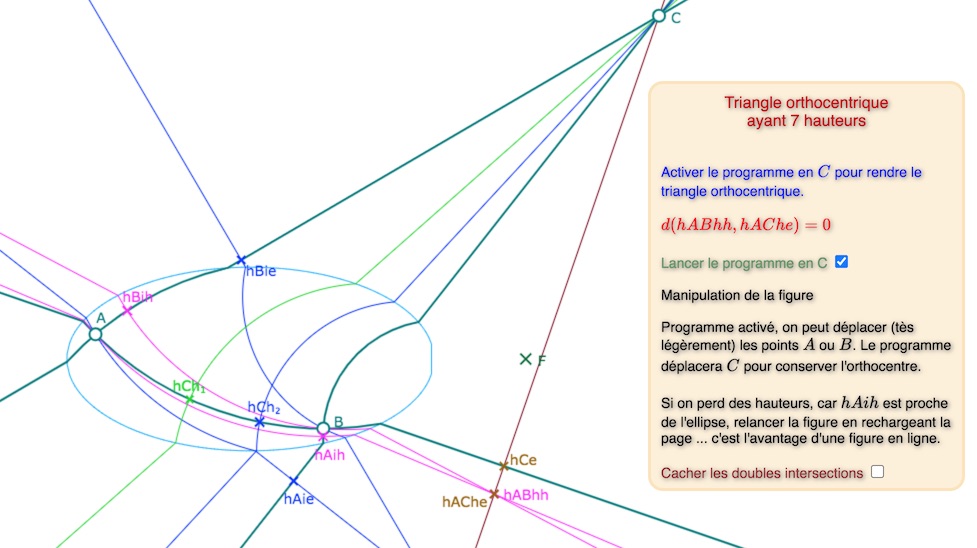
Montrons quand même le triangle orthocentrique obtenu …
Le cas de hauteurs parallèles
Cette géométrie nous réserve quelques autres surprises. Voici une figure comportant plusieurs configurations de triangles dont deux hauteurs sont parallèles.
Principe de ce type de figures.
On aura compris, en voyant les coefficients algébriques en jeu qu’il n’est pas question de chercher algébriquement ni le parallélisme de deux hauteurs ni le concours formel de trois hauteurs. Par contre on peut trouver des solutions, à la précision de l’ordinateur (en pratique à \(10^{-13}\), la précision du JavaScript, et donc largement au delà du millionième de pixel), des constructions où il y a concours des hauteurs (comme on l’a déjà fait pour les médianes), ou, comme ici, le parallélisme de deux hauteurs. Pour cela on se rapproche « à la main » d’une solution, et on modifie la position d’un sommet du triangle par itérations successives jusqu’à la précision maximale. En voici une première illustration
Choisir une configuration, activer le programme pour voir l’effet, puis le désactiver avant de changer de configuration.
Dans le mode \(Libre\), on peut déplacer légèrement un des points \(B\) ou \(C\) avec le programme activé
(en relâchant pour le programme aille à son terme) … a priori, cela fonctionne.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.
Dans les pages suivantes on va s’intéresser à l’exploration de triangles orthocentriques de la même façon, avec des programmes qui finalisent le concours des hauteurs, et, dans un second temps, on abordera le régionnement du plan en fonction du nombre de perpendiculaires pour une droite donnée.