La représentation de la pseudosphère
La pseudosphère a comme représentation paramétrique \(\displaystyle \left( \frac{1}{ch \; u}cos \theta,\frac{1}{ch \; u}sin \theta,u -th \; u \right),\; \theta \in \mathbb{R}, \; u>0\)
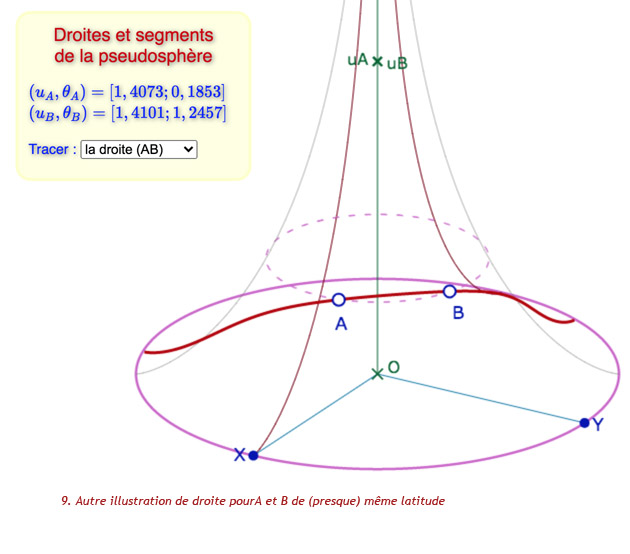
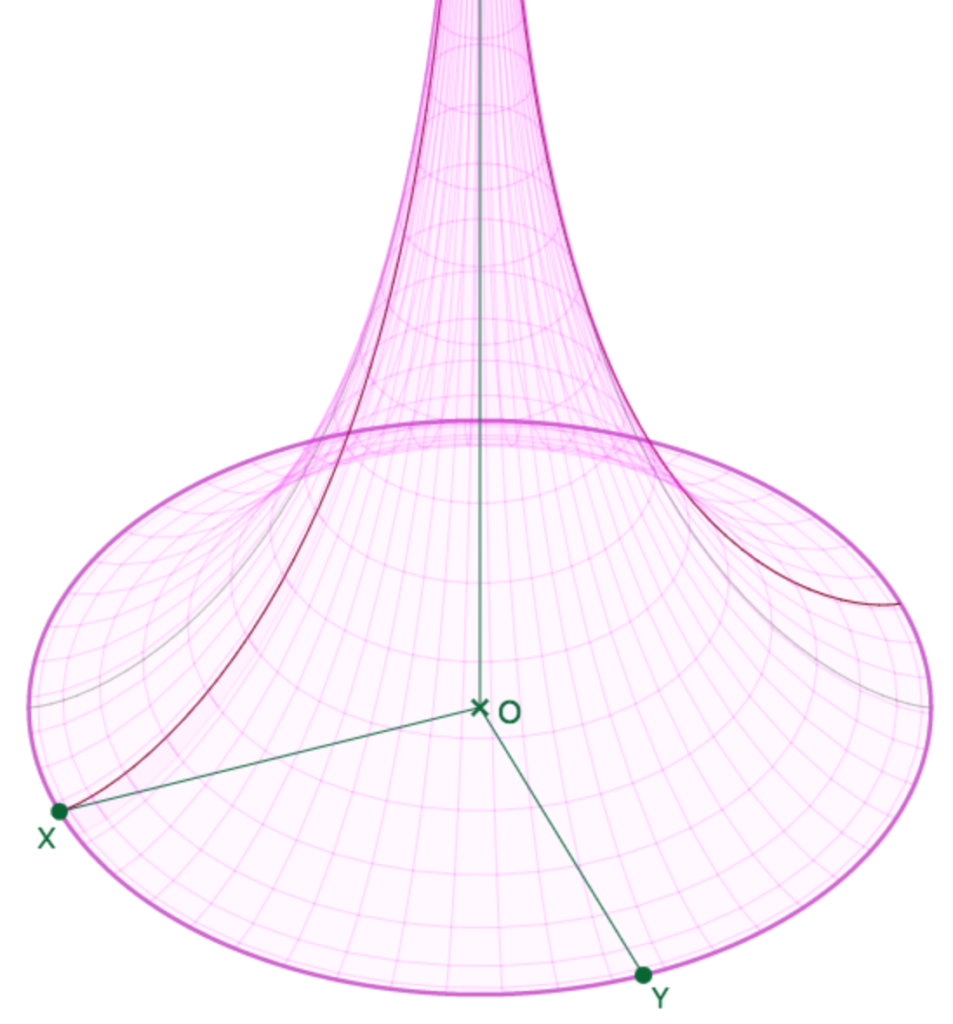
La feuille principale de la pseudosphère va de \(0\) à \(2\pi\), depuis la générique passant par le point \(X\) jusqu’au même point après un tour. Ainsi la générique – non tracée – passant par le point \(Y\) est de longitude \(\frac{\pi}{2}\). La générique, tracée, passant par le symétrique de \(X\) par rapport à l’origine du repère est de longitude \(\pi\).
On a choisi de tracer deux autres génériques, plus fines, en gris, qui partent des sommets du grand axe de l’ellipse représentant l’équateur dans la vue axonométrique à l’écran.
Les points de la surface sont, de fait, sur un cercle parallèle à l’équateur. Ce cercle a une latitude, au sens de de la paramétrisation de la pseudoshère, et une longitude, sur ce cercle.
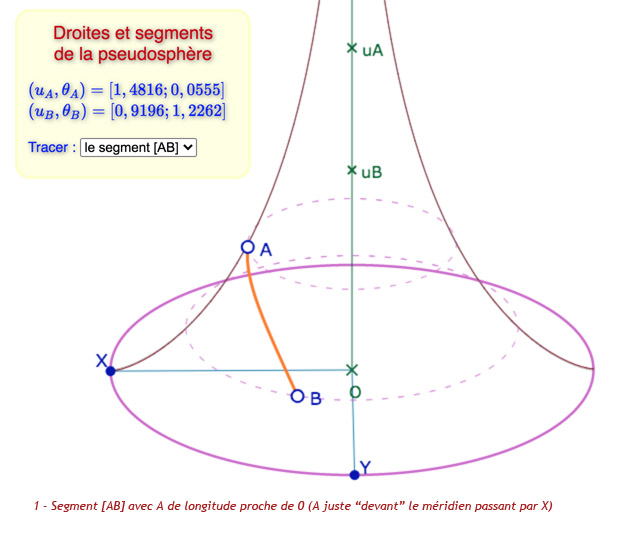
Pour définir un point \(A\) en manipulation directe sur la pseudosphère, on se donne une latitude \(u_A\) sur l’axe vertical qui représente l’axe de la pseudosphère. De cette latitude on construit le cercle parallèle à l’équateur de côte \(u_A – th \; u_A\) sur lequel on prend ce point \(A\). Ce point placé sur le cercle, on calcule simplement sa longitude \(\theta_A\) dans le repère associé à (XOY).
Compte tenu du déterminisme des logiciels de géométrie dynamique, on a nécessairement \(0 < \theta_A < 2\pi\). Cela signifie que, de par la conception même des logiciels, les points de base posés sur la pseudosphère le sont sur sa feuille principale. cela n’empèchera pas de construire des droites sur plusieurs feuilles, mais – dans un premier temps – on ne pourra pas enrouler continûment un point, à la souris, sur plusieurs feuilles de la pseudosphère : on retrouve ici, en terme de questionnement de la géométrie dynamique, des interrogations qui ressemblent à celles présentes à l’époque de Minding.
Les droites de la pseudosphère
Les géodésiques de la pseudosphère sont de deux sortes :
• les méridiens, d’équation \(\theta = c\)
• les autres droites d’équation \(ch^2(u)+(\theta+c)^2=k^2\) où \(c\) et \(k\) sont deux constantes.
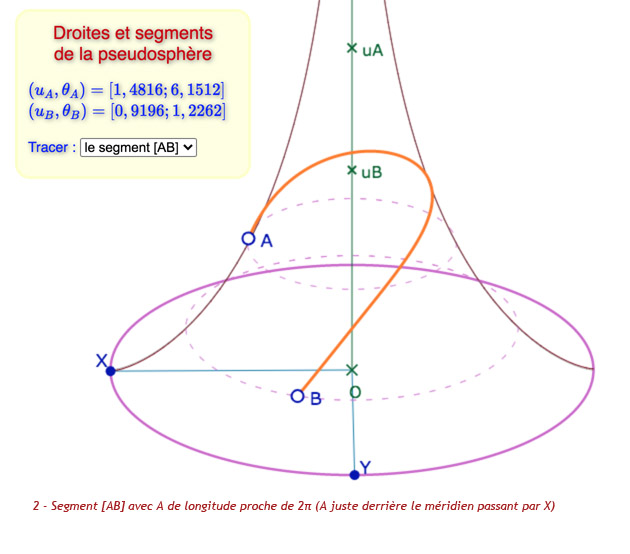
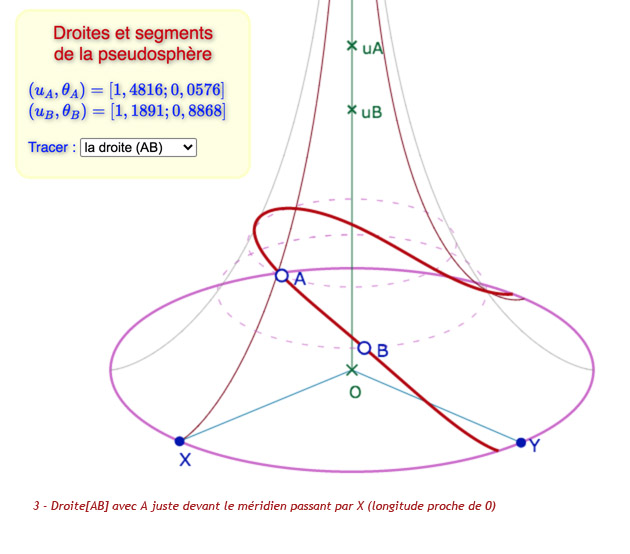
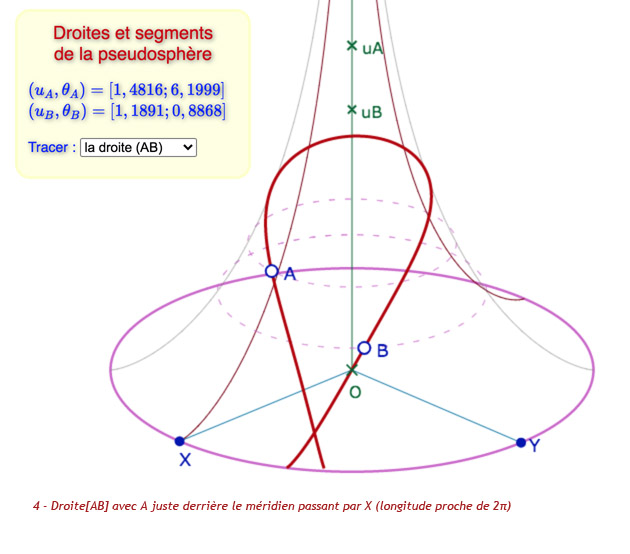
En dehors des méridiens qui vont tous vers un même point à l’infini – ce qui apparaitra clairement plus loin – il est immédiat que les autres droites vont de l’équateur (\(u=0\)) à l’équateur en passant par un maximum pour \(\theta =-c\) , donné par \(ch^2(u)=k^2\). Mais si elles « redescendent » à l’équateur, elles n’y vont pas sur une seule feuille, on parlera de droites multifeuilles. Pour ces feuilles, l’amplitude de la longitude doit être maximale, maximum atteint quand \(ch(u)\) est minimum, et donc vaut 1. Les extrémités, sur l’équateur, sont atteintes pour \(\theta = -c – \sqrt{k^2-1}\) et \(\theta = -c + \sqrt{k^2-1}\)
Droite passant par deux points
Étant donnés deux points \(A(u_A, \theta_A)\) et \(B(u_B, \theta_B)\), avec \(\theta_A \ne \theta_B\), les constantes de la géodésique \((AB)\) sont données par :
\(\displaystyle c_{AB}=\frac{ch^2(u_A)+\theta^2_A-ch^2(u_B)-\theta^2_B}{2(\theta_B-\theta_A)}\) et donc \(k^2_{AB}=\sqrt{ch^2(u_A)+(\theta_A+c_{AB})^2}\).
C’est parce que ces deux constantes s’expriment aisément à partir des coordonnées de \(A\) et \(B\) que l’on peut construire les droites sur la pseudosphère de manière intrinsèque, simplement avec les outils de géométrie différentielle.
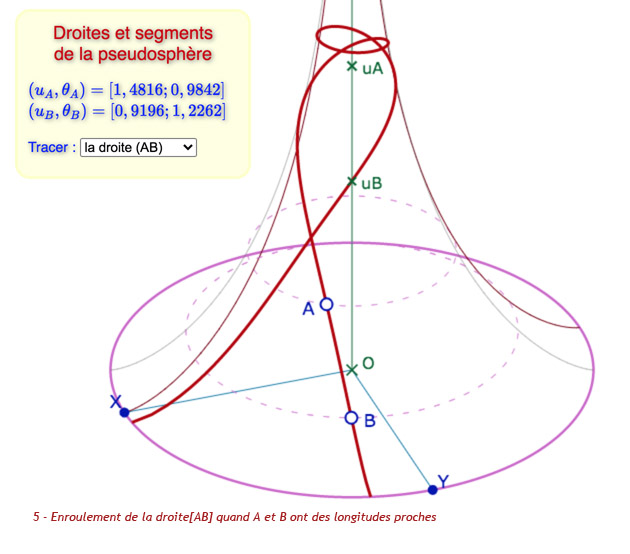
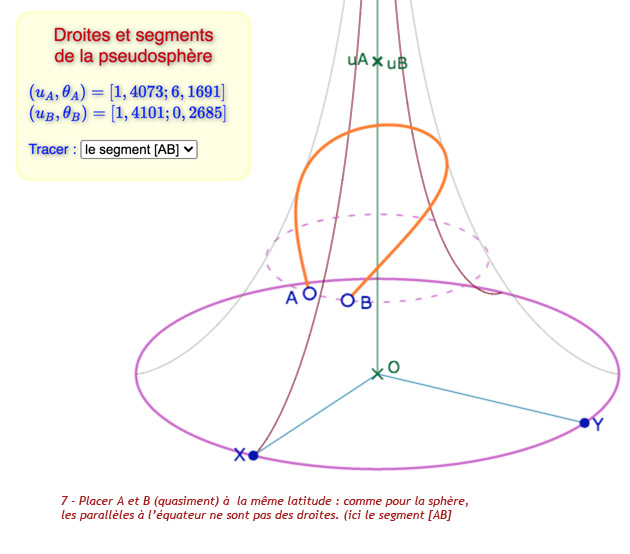
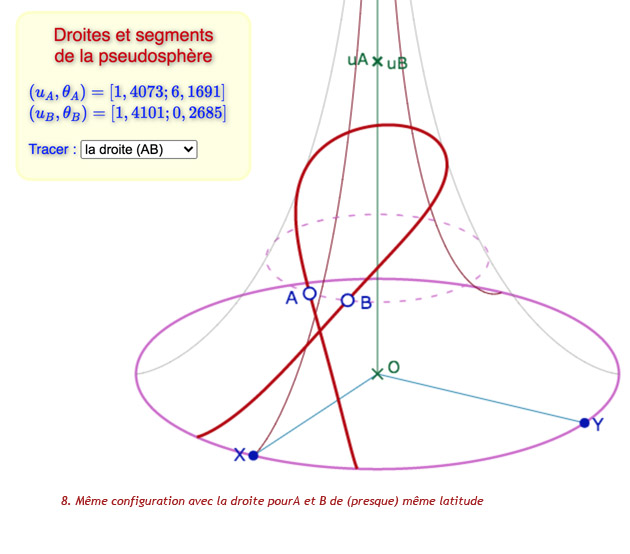
Galerie de neufs situations que l’on peut explorer plus en détail dans la figure suivante
La figure correspondante
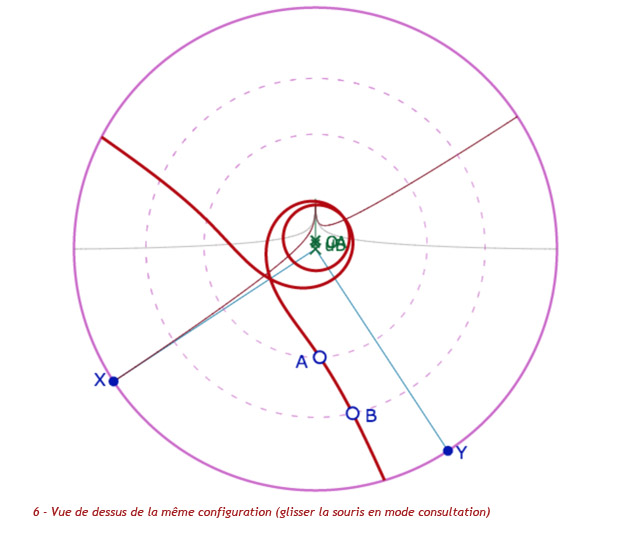
Penser à tourner la pseudosphère et à la pencher vers l’avant
pour voir la droite de dessus, comme dans l’illustration 6.
Points multifeuilles – Une première approche par pop-up
Une façon simple de placer des points sur d’autres feuilles consiste à les déclarer, un peu artificiellement, comme tels, et d’ajouter ou retrancher un multiple de \(2\pi\) pour la longitude. Dans la figure suivante, chaque sommet \(A, B, C\) du triangle peut être sur trois feuilles, la principale et ses deux adjacentes.
Observer la variation des longitudes pour un point donné en le changeant de feuille.
Penser au « mode avion » pour voir le triangle de dessus
Enroulement continu multifeuille
Mais pour la géométrie dynamique, l’idéal serait de pouvoir faire tourner des points continument d’une feuille à l’autre. Cela avait été possible avec CaRMetal (mais en java donc désormais plus utilisable en ligne). En cours de réflexion … En attendant, ce menu est developpé avec, parfois, les figures « en pop up » pour le multifeuille.