Perpendiculaire à (AB) passant par C pour C n’appartenant pas à (AB)
(sinon le dénominateur de la longitude est nul)
Le pied de la perpendiculaire a pour longitude \(\theta_H = \displaystyle \frac{2\theta_Ck^2_{AB}-c_{AB}\left(ch^2u_C+(\theta_B+c_{AB})^2-k^2_{AB}\right)}{ch^2u_C+(\theta_B+c_{AB})^2+k^2_{AB}}\) ce qui permet de construire le point et ensuite la droite.
Illustration avec les hauteurs d’un triangle
Comme pour les autres figures, agir sur les sommets et leurs latitudes
Perpendiculaire à (AB) passant par un point C de la droite (AB)
On trouve plus simplement les constantes de la perpendiculaire, qui se construit alors par la macro « Droite par constantes », soit \(c_{ortho}= c_{AB}- \displaystyle \frac{k^2_{AB}}{\theta_C+c_{AB}}\) et \(k^2_{ortho}=\displaystyle \frac{k^4_{AB}}{(\theta_C+c_{AB})^2}-k^2_{AB}\)
La première application est bien entendu la construction des médiatrices d’un triangle
\(o_{ABC}\) est le centre du cercle circonscrit quand il existe … et qu’il existe sur la pseudosphère
Préférer ouvrir la figure en plein écran dans un nouvel onglet
Perpendiculaire commune à deux droites
La perpendiculaire commune à deux droites \(d_1 \; (k_1, c_1)\) et \(d_2 \; (k_2, c_2)\) est la droite \((H_1H_2)\) avec \(H_1 \in d_1\) et \(H_2 \in d_2\), données par leurs longitudes \(\theta_1\) et \(\theta_2\) vérifiant :
\(\theta_1 = -c_1 \displaystyle + \frac{2(c_1-c_2)k^2_1}{(c_1-c_2)^2+k^2_1-k^2_2}\) et \(\theta_2 = -c_2 \displaystyle + \frac{2(c_2-c_1)k^2_2}{(c_2-c_1)^2+k^2_2-k^2_1}\).
Plusieurs remarques : deux droites peuvent être sécantes en dehors de la pseudosphère et donc ne pas avoir de perpendiculaire commune. Elles peuvent avoir aussi une perpendiculaire commune en dehors de la pseudosphère. On peut même avoir un des deux pieds de la perpendiculaire commune sur la pseudosphère et pas l’autre. Tout ceci sera plus clair quand on illustrera le lien avec le disque limite de Beltrami (le modèle de Klein Beltrami).
Dans les macro réalisées, la perpendiculaire commune n’est construite que si les deux points \(H_1\) et \(H_2\) sont bien sur la pseudosphère.
Exemple du pinceau des médiatrices sur la pseudosphère
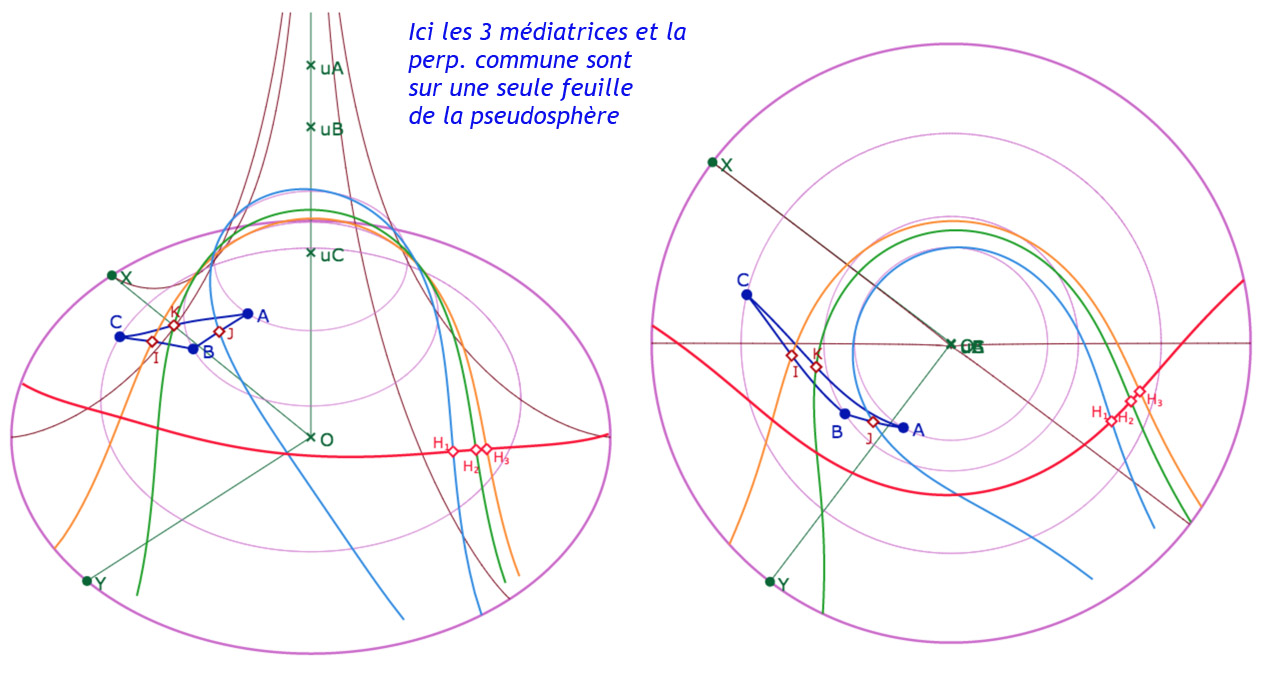
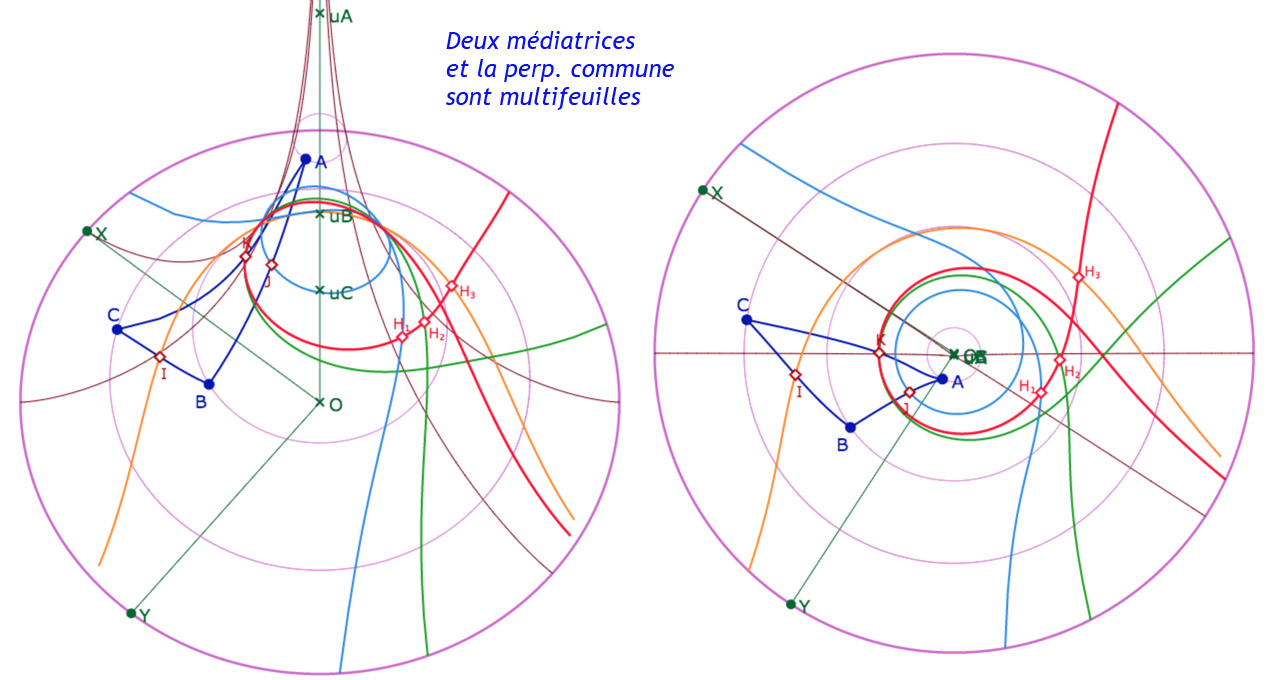
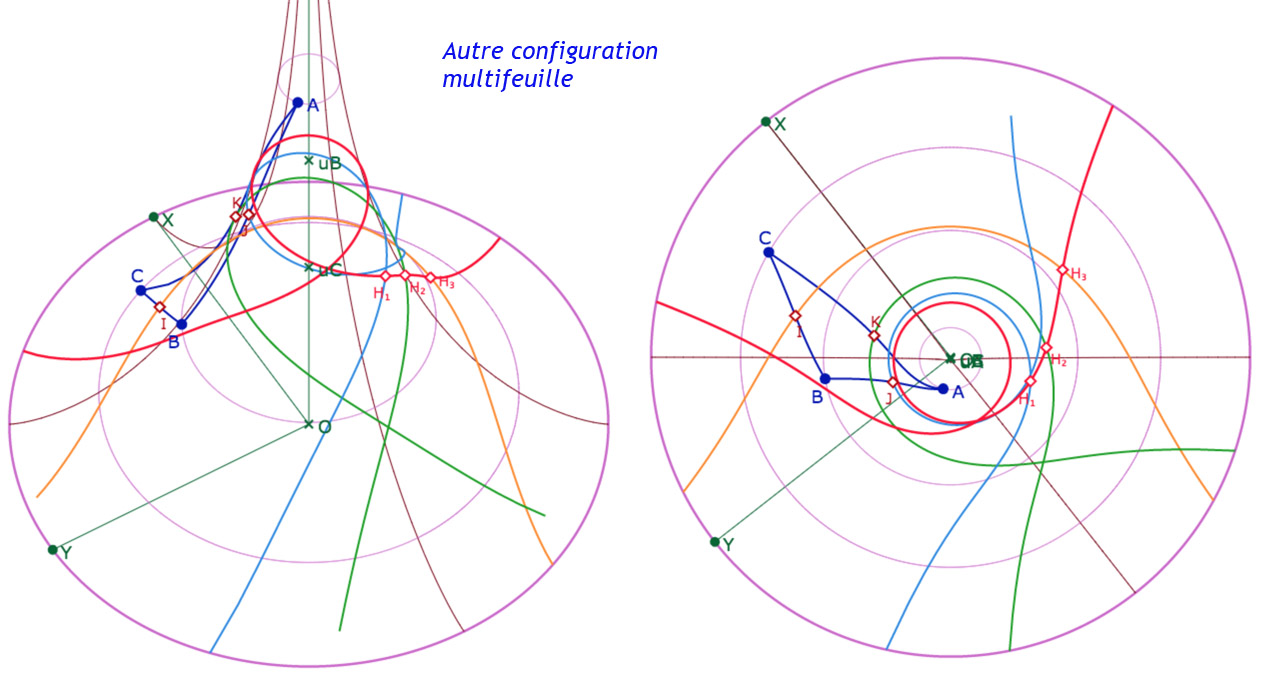
On a vu – dans le menu DP sur le disque de Poincaré – que les médiatrices d’un triangle sont en pinceau, c’est-à-dire ont un point commun ou une perpendiculaire commune (ou sont parallèles mais non visible sur la pseudosphère dans le cas général). Dans la figure suivante, on reprend la figure des médiatrices et on y ajoute la perpendiculaire commune aux médiatrices – quand elle existe – avec ses trois intersections avec les médiatrices. Voici quelques illustrations de la figure suivante.
Galerie de présentation de la figure suivante (4 double-illustrations)
La figure associée
On rappelle qu’entre le moment où le pinceau est à centre sur la pseudosphère où à axe sur la pseudosphère, il existe un passage où le pinceau est à centre sans qu’il soit visible sur la pseudosphère où à axe sans qu’il soit visible sur la pseudosphère.
Agir sur les points \(A\), \(B\), \(C\) et/ou leurs latitudes.
Il faut « pencher » la pseudosphère vers l’avant pour accéder à la latitude \(u_A\).
Préférer ouvrir la figure en plein écran dans un nouvel onglet
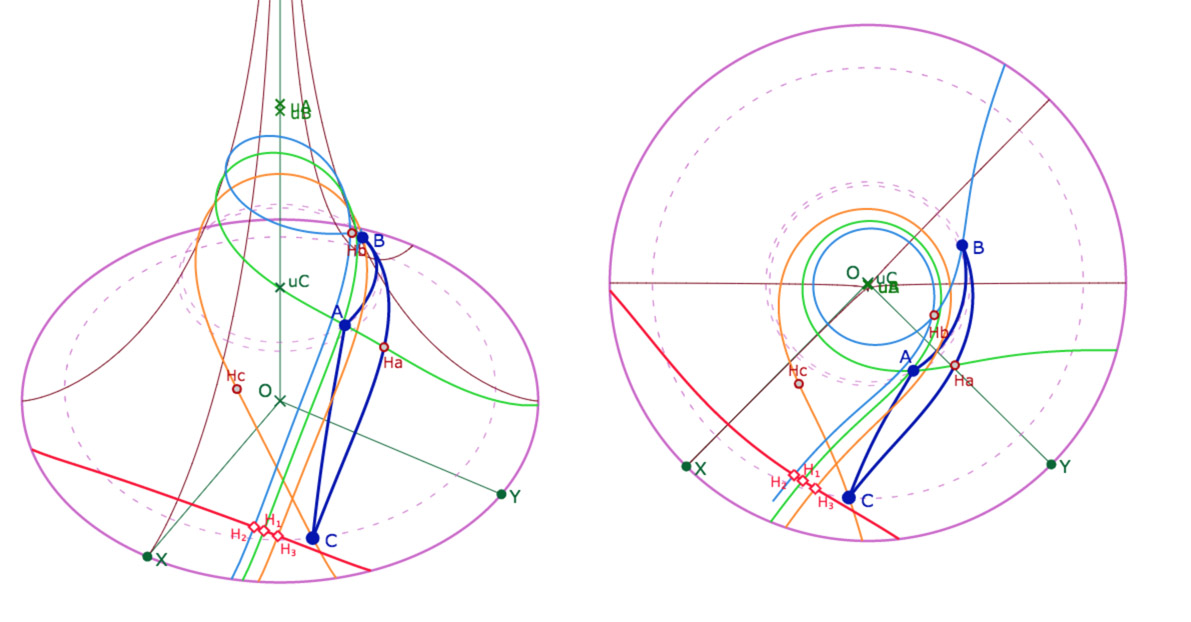
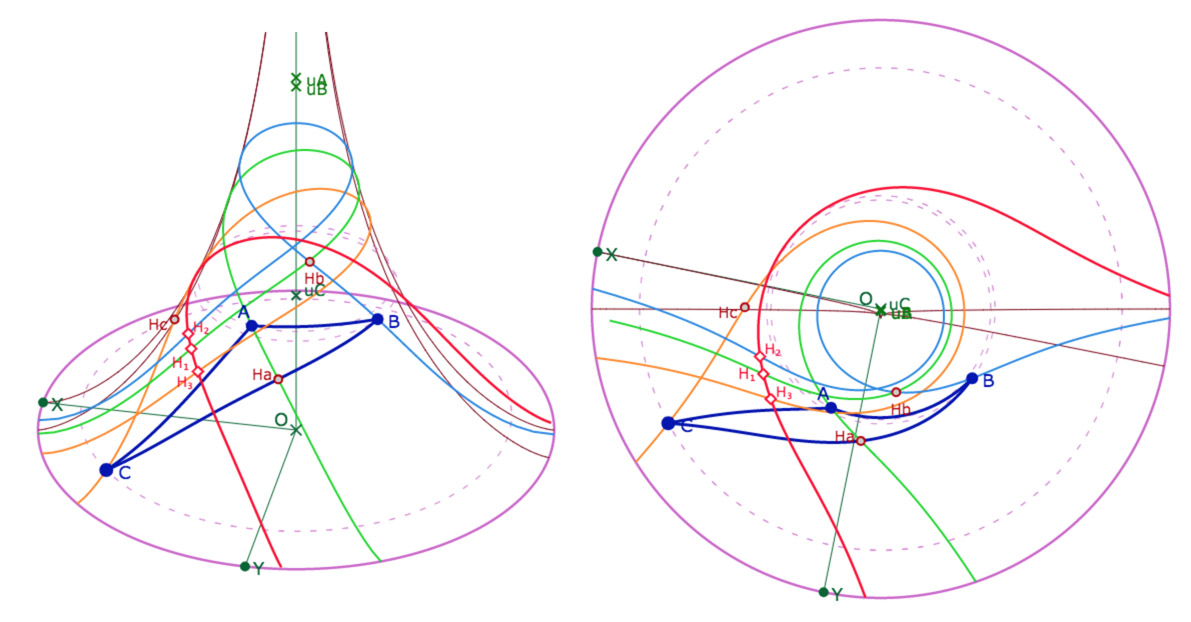
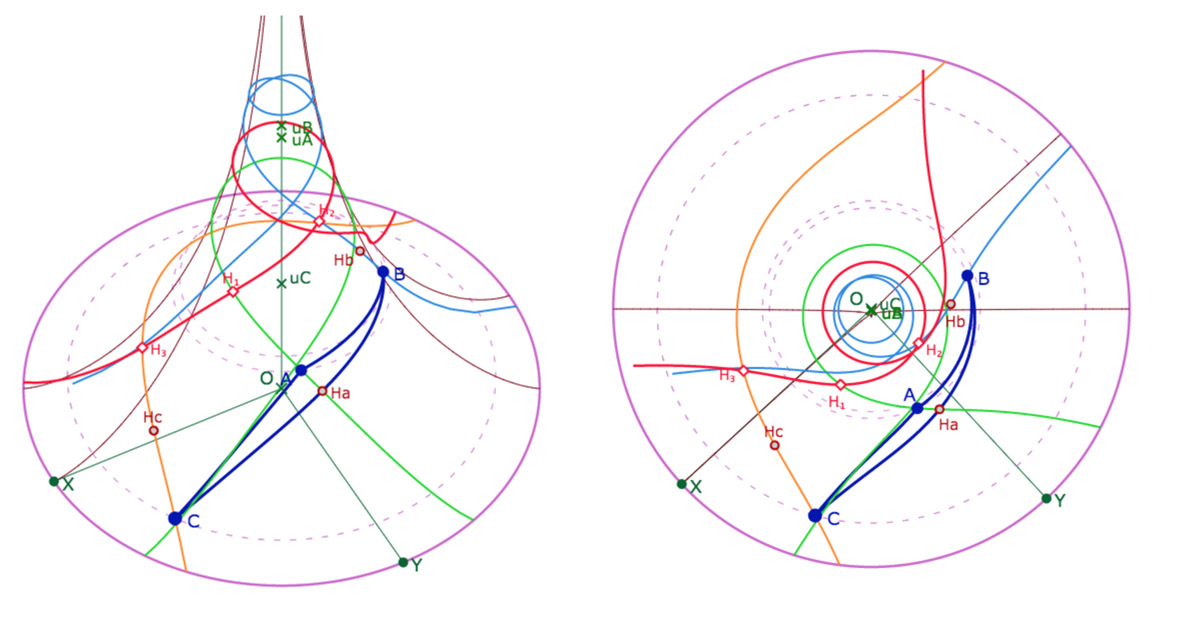
Exemple du pinceau des hauteurs
Pour ne pas alourdir la visibilité de la figure, on a conservé le triangle avec des segments. Deux pieds des hauteurs sont alors en dehors du segment du triangle.
Galerie de trois exemples de configurations sur la perpendiculaire commune aux trois hauteurs d’un triangle.
La figure associée
Même démarche que les autres figures. La situation est plus sensible qu’avec les médiatrices
(déplacer les points lentement, de quelques pixels seulement)
Préférer ouvrir cette figure en plein écran dans un nouvel onglet