Dans la page précédente, nous avons vu plusieurs configurations à cinq hauteurs pour lesquelles, il ne pouvait y avoir deux orthocentres, avec un argument élémentaire : une hauteur ne peux pas être perpendiculaires à deux droites non parallèles. Mais cet argument s’il est très général, peut aussi ne pas s’appliquer à certains cas biens particuliers. Voyons un premier exemple élémentaire.
Un triangle bi-orthocentrique particulier
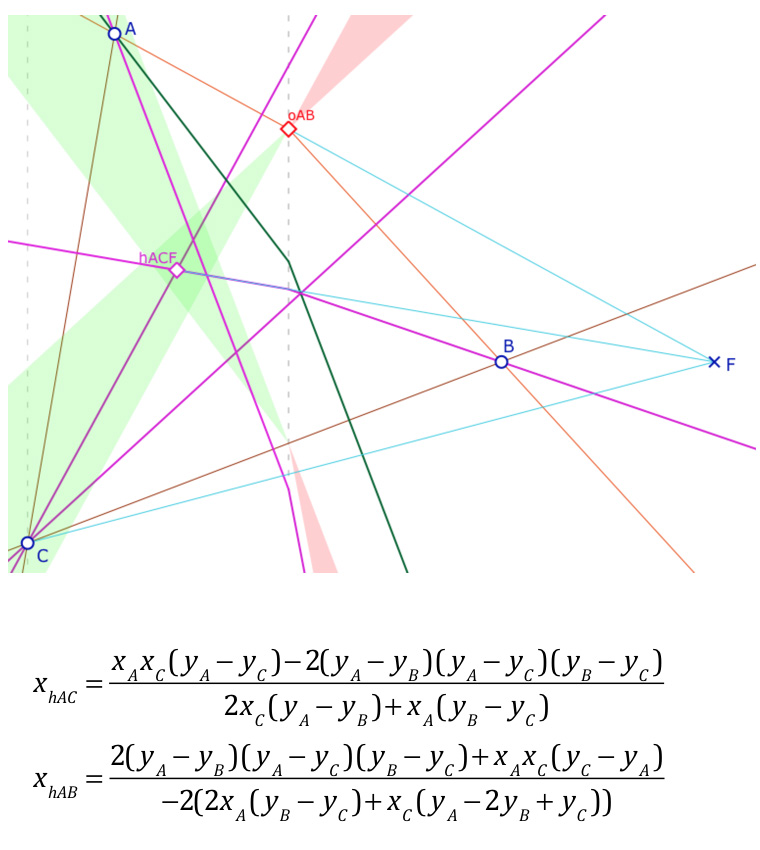
Lors du « Cas 3 » de la page précédente (orthocentre réalisé dès que \(x_C= \displaystyle \frac{3x_A}{2}\)), illustré ci-contre, nous avons vu que \(h_{ACF}\) ne peux pas être un orthocentre car il faudrait que la hauteur issue de \(A\), perpendiculaire à \((CB)\) soit aussi orthogonale à \((CF)\), ce qui est impossible, en particulier car \(x_F = 2x_B\).
Impossible … sauf si \(x_B=0\) !
Or, dans ce cas – soit \(B\) sur l’axe des ordonnées – l’orthocentre à abscisse positive existe toujours, mais en plus, même si la droite de Moulton \((AB)\) est bien à pente négative, le triangle est aussi euclidien, et comme tel admet aussi un orthocentre euclidien.
Avec \(x_B=0\), les coordonnées des intersections \(x_{hAC}\) et \(x_{hAB}\) des hauteurs de Moulton se simplifient comme indiqué ci-contre.
Figure dynamique d’un premier M-triangle bi-orthocentrique
On peut déplacer \(A\) et \(C\) en les laissant dans les «zones vertes», et \(B\) sur l’axe vertical.
Penser à sortir \(C\) du magnétisme la droite solution de l’orthocentre d’abscisse positive.
Préférer ouvrir la figure dans un nouvel onglet
Triangle bi-orthocentrique plus général
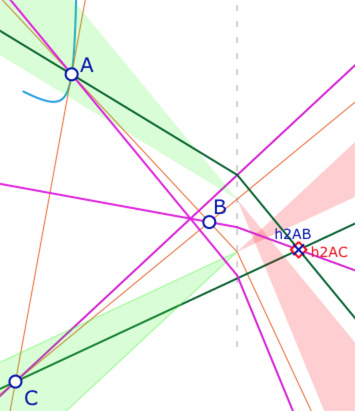
On reste sur une figure proche du « Cas 3 » de la page précédente, rappelé ci-dessus : une droite \((AB)\) à pente négative et les deux autres côtés à pente positive, avec, bien évidemment, une configuration à cinq hauteurs. Une façon simple de construire un triangle avec deux orthocentres consiste à partir d’une figure ayant déjà un orthocentre euclidien et chercher les conditions pour les hauteurs supplémentaires, issues de \(A\) et \(C\) soient sécantes sur l’unique hauteur issue de \(B\).
Une solution est possible dans le contexte suivant :
– \(A, B, C\) et l’orthocentre euclidien de \(ABC\) sont tous à abscisse négative.
– La droite \((AB)\) est à pente négative, les droites \((BC)\) et \((AC)\) sont à pente positive
– Le triangle de Moulton \(ABC\) a deux hauteurs issues de \(A\) et \(C\).
Dans ce contexte,on note \(h_{2AB}\) l’intersection de la «seconde» hauteur (verte) issue de \(A\) et de la hauteur issue de \(B\) et \(h_{2BC}\) l’intersection de l’autre «seconde» hauteur verte issue de \(C\) et de la hauteur issue de \(B\).
Alors on a :
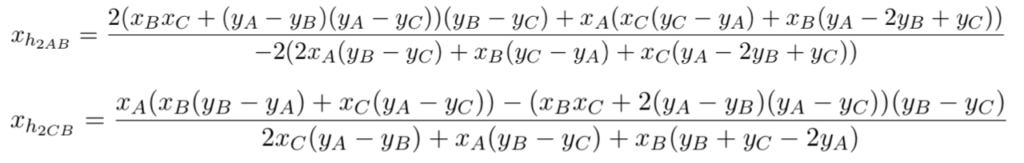
En égalant les deux abscisses, on obtient une relation de laquelle on peut exprimer l’ordonnée d’un des points \(A\), \(B\), ou \(C\) en fonction des cinq autres coordonnées. En pratique, pour une manipulation dynamique, il n’est pas judicieux de choisir le point \(B\) car les deux parties à deux perpendiculaires dépendent directement de \(B\). Il est préférable de choisir \(A\) ou \(C\). On a choisit le point \(A\). Dans ce cas, l’expression de l’ordonnée de \(A\) est de Type (1) – notations de la page précédente – avec les paramètres suivants :
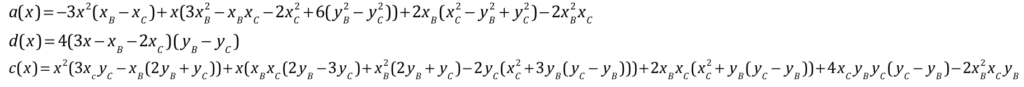
Déplacer \(A\) sur sa courbe, \(C\) ou encore \(B\), mais lentement et avec modération … car tout dépend de \(B\).
Préférer ouvrir la figure dans un nouvel onglet