Suite à la construction algébrique générale d’une droite de Hilbert (H-droite), voici le détail de mise en œuvre de quelques macros techniques. Cette page est surtout une page d’archivage des méthodes utilisées, mais, pour quelques lecteurs, elle peut être intéressante à consulter pour les techniques utilisées. Nous aborderons ainsi :
• la réalisation d’un « point sur objet » d’une H-droite
• la construction d’une H-droite parallèle à une droite donnée.
• l’intersection de deux H-droites.
• le calcul de la H-distance entre deux points (ou H-Longueur d’un segment)
• la construction du H-milieu de deux points
Prendre un point sur objet d’une H-droite
Une H-droite est, soit une droite affine ordinaire si elle ne coupe pas l’ellipse – ou lui est tangente, soit est composée de deux demi-droites et un arc de cercle, qui sont trois objets distincts pour un logiciel de géométrie dynamique. On peut néanmoins arriver à simuler – en manipulation directe – un unique point et l’utiliser comme tel dans les macros de construction. Voyons comment.
Macro « Constituants d’une droite«
Une première macro, qui servira à toutes les autres consiste juste à faire apparaitre les points constituants d’une H-droite.
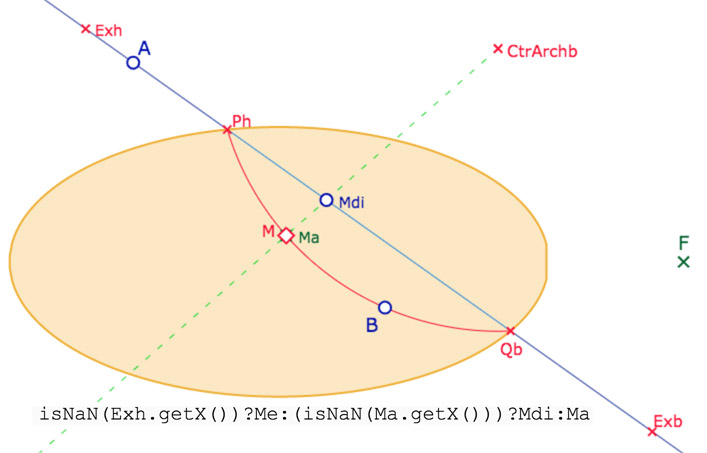
La macro, à partir des trois parties d’une H-droite non affine (une demi-droite, l’arc de cercle, l’autre demi-droite), renvoie cinq points : \(Ex_h, Ex_b\) qui servira pour le « point sur objet », la pente d’une droite, et les points constituants de l’arc de cercle \(P_h, P_b, CtrArc{hb}\) qui eux serviront aussi pour les macros H_Longueur et H-milieu.
Construire un point sur objet de la droite
Sur la droite affine \((Ex_h Ex_b)\), on prend un point \(M_{di}\) (\(_{di}\) pour « droite » et « intérieur »). C’est essentiellement pour cela que les points \(Ex_h\) et \(Ex_b\)ont été crées :
• d’une part, ils sont dans une position stable quand la droite d’intersection \((U_{gg} V_{gg})\) de la page précédente change d’orientation, et donc un point sur objet de cette droite a un comportement barycentrique indépendant de l’orientation de la droite.
• ensuite, les points étant plus éloignés que \(P_h\) et \(Q_h\), donc ce même comportement barycentrique est plus fluide.
lQuand \(M_{di}\) est à l’intérieur de l’ellipse on construit le point \(M_a\) sur l’arc. Ensuite on prend un point \(M_e\) sur la droite affine \((AB)\). On peut alors construire le point \(M\) comme indiqué dans l’illustration ci-dessus : le point \(M\) est
• en \(M_e\) si la droite \((AB)\) ne coupe pas l’ellipse
• en \(M_a\) quand \(M_{di}\) est dans l’ellipse, en \(M_{di}\) sinon.
Pour améliorer l’expérience utilisateur, on cache le nom des trois points \(M_e, M_a, M_{di}\) on pense alors agir sur \(M\) alors qu’on agit sur les points \(M_e\) ou \(M_{di}\). Enfin, quand \(M_{di}\) est dans l’ellipse, il a alors l’habillage d’un point rouge (produit par Blockly).
Exemple d’utilisation : la version projective de la propriété de Desargues
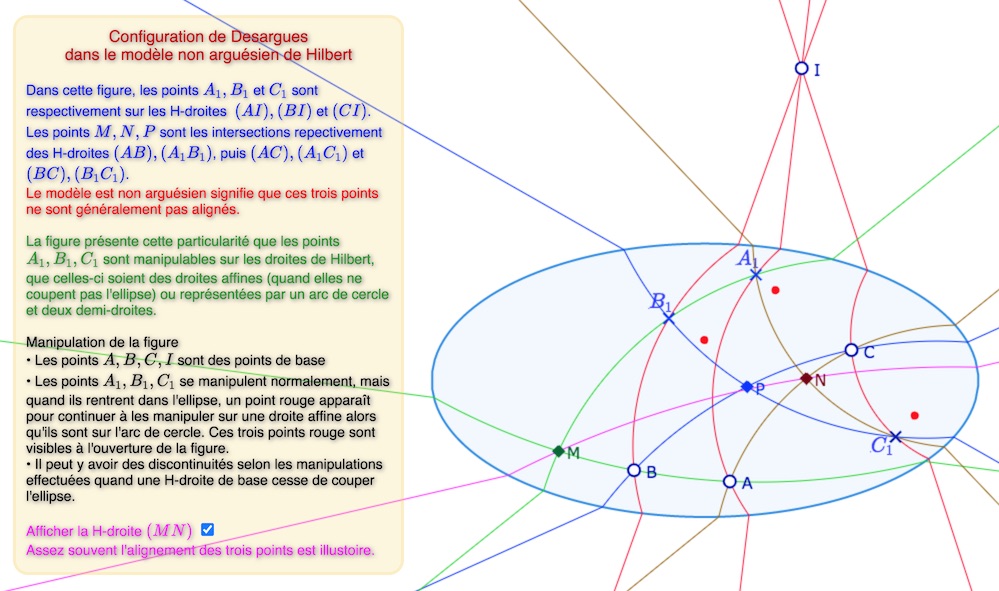
Les trois points rouges sont les points de manipulation des points \(A_1, B_1, C_1\) quand ils sont intérieurs à l’ellipse.
Les points \(M, N, P\) sont construits par une macro Intersection détaillée plus loin
Ouvrir cette figure dans un nouvel onglet.
H-parallèle à une H-droite
Le seul cas délicat est celui de la construction d’une parallèle à une H-droite passant par un point \(M\) en intérieur à l’ellipse. En notant \(a\) la pente de la droite dont on doit prendre une parallèle, on cherche le paramètre \(b\) tel que la droite d’équation \(y=ax+b\) soit le support affine de l’extérieure à l’ellipse de la droite cherchée. En utilisant la même démarche que pour la H-droite, soit la formule de Ptolémée sur la cocyclicité des points \(M,F\) et les intersections \(Pph, Qph\) de la droite avec l’ellipse,
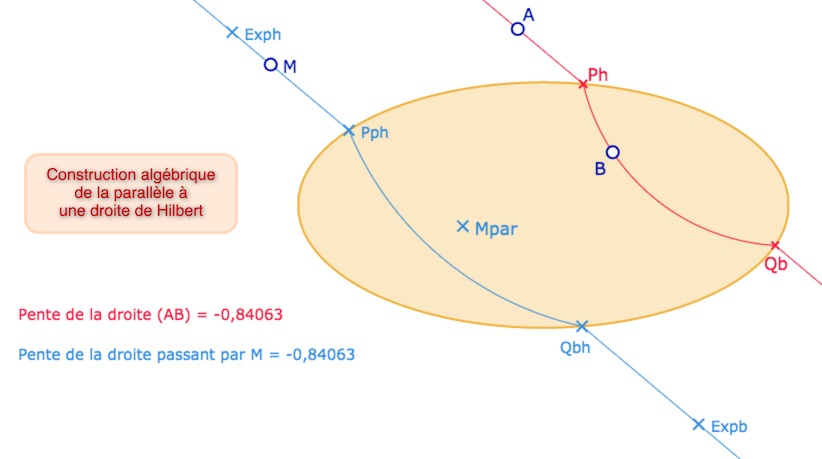
Le calcul formel donne deux coefficients \(b_1, b_2\), mais seul premier convient, l’autre correspond à des intersections imaginaires avec l’ellipse. Ce coefficient \(b_1\) s’écrit alors :

Ici, le point \(A(x_A, y_A)\) est le point de la droite cherchée, intérieur à l’ellipse
La construction de la droite parallèle peut alors se résumer ainsi :
La pente pAB de la droite initiale
isNaN(Exh.getX())?(y(B)-y(A))/(x(B)-x(A)):(y(Exb)-y(Exh))/(x(Exb)-x(Exh))
coef b si M (xM,yM) est intérieur
-(1/(12(pAB(-3+2xM)+2yM)))(-9-36pAB^2+4xM^2+16pAB^2xM^2+36pAByM+4yM^2+16pAB^2yM^2+sqrt((-9+4xM^2+36pAByM+4yM^2+4pAB^2(-9+4 xM^2+4 yM^2))^2-24(pAB(-3+2xM)+2yM)(5yM+32pAB^2yM+pAB(-6-5xM+6xM^2+6yM^2)+pAB^3(-6-32xM+24xM^2+24yM^2))))
On nomme Upii et Vpii les points de l’ellipse si M est intérieur
On les nomme Upie Vpie si M est extérieur et que la droite parallèle coupe l’ellipse. Pour cela il faut prendre la parallèle à (AB) dans les deux cas où (AB) coupe l’ellipse et le cas où elle ne coupe pas. D’où la construction de ce point conditionnel (la droite parallèle passe alors par M et ce point)
Mpar : (isNaN(Exh.getX()))M+B-A:M+Qb-Ph
On prend ensuite les points Upg et Vpg qui sont soit l’un de ces deux points – si ils existent – soit aucun si
• un couple n'existe pas • la parallèle ne coupe pas l'ellipseUpg : (Mint==0)?Upie:Upii
Vpg : (Mint==0)?Vpie:Vpii
Et enfin on prend Pph et Qpb comme pour la droite
Pph : (y(Upg)>y(Vpg))?Upg:Vpg
DtrPar.setHidden((ptMint==1)||(!isNaN(Pph.getX()))); »cacher la parallele »
La pente de la parallèle ainsi construite
isNaN(Exph.getX())?(y(Mpar)-y(M))/(x(Mpar)-x(M)):(y(Exph)-y(Expb))/(x(Exph)-x(Expb))
Exemple de réalisation (avec les macros suivantes de longueur et de milieu)
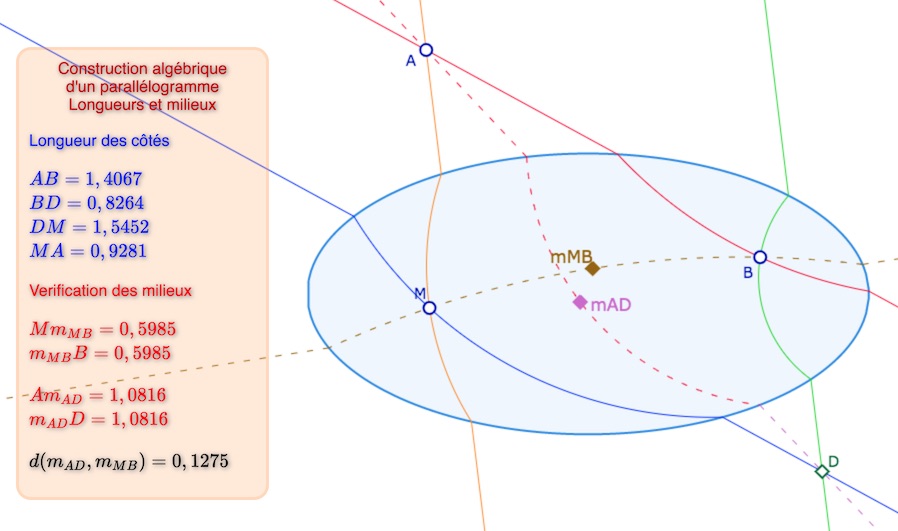
Ouvrir cette figure dans un nouvel onglet
Les milieux peuvent être confondus sans que les côtés soient de même longueur :
• comme ici, exactement
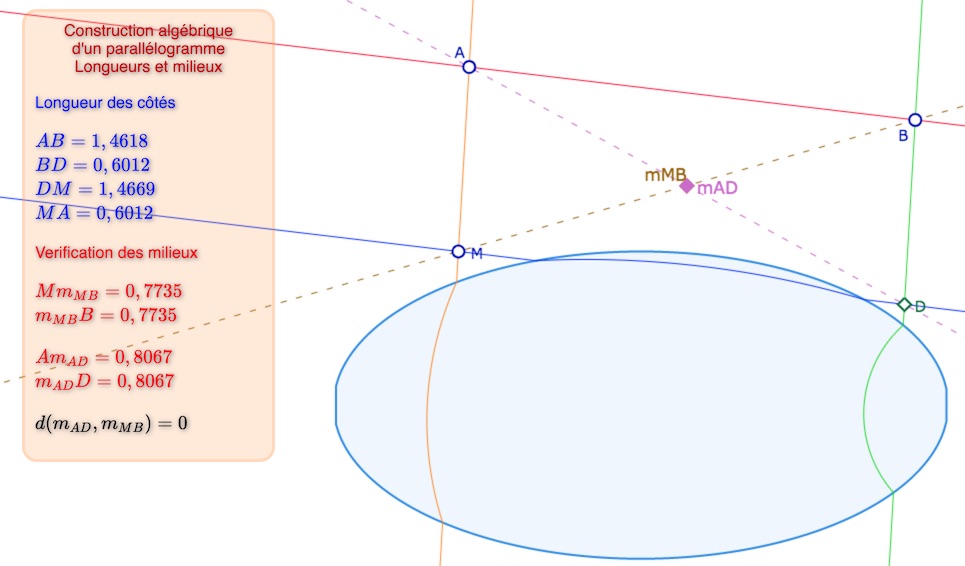
• ou comme là, approximativement (en attendant une construction)
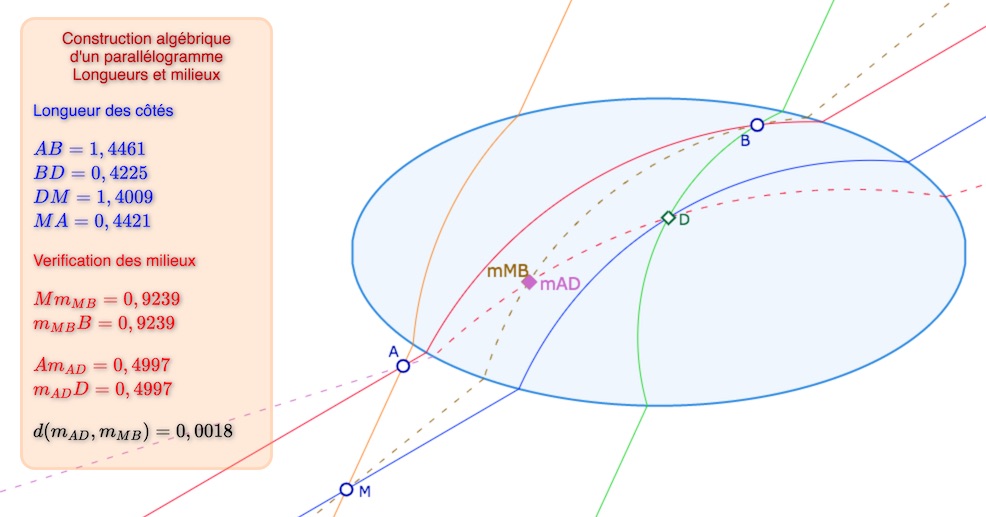
Intersection de deux H-droites
Dans les deux figures précédentes, il a fallu construire l’intersection de deux H-droites : ci-dessus pour le point \(D\) et dans la figure de Desargues, pour les points \(M, N, P\). D’une manière générale l’intersection de deux H-droites peut être l’intersection de :
• deux arcs de cercle si l’intersection est à l’intérieur de l’ellipse, on la notera \(M_i\),
• des deux droites support des droites affines (de type \((Ex_h Ex_b)\), on la notera \(Md_{ii}\), cas qui contient lui-même 4 intersections possibles de demi-droites, d’où l’intérêt de construire ces droites support.
• d’une droite affine (quand cette droite ne coupe pas l’ellipse) et d’une droite support du type précédent. ll y a alors deux telles possibilités, que l’on notera génériquement \(Mdd_{i}\) et \(Md_{i}d\) (avec \(d\) pour la droite affine et \(d_{i}\) pour la droite support qui passe à l’intérieur de l’ellipse,
• enfin des deux droites affines quand ces deux droites ne coupent pas l’ellipse.
Comme, à part le premier cas, les autres points peuvent exister simultanément, il faut prendre les intersections possibles dans un ordre bien établi. L’intersection finale peut alors s’écrire sous cette forme de 4 conditions imbriquées :
isNaN(Mi.getX())?(isNaN(Mdii.getX()))?(isNaN(Mddi.getX()))?(isNaN(Mdid.getX()))?Mdd:Mdid:Mddi:Mdii:Mi
Longueur d’un segment
La H-longueur entre deux points \(A\) et \(B\) est la longueur euclidienne d’un ou deux segments avec éventuellement l’ajout d’un arc de cercle. La macro doit traiter les différents cas présentés ci-dessous.
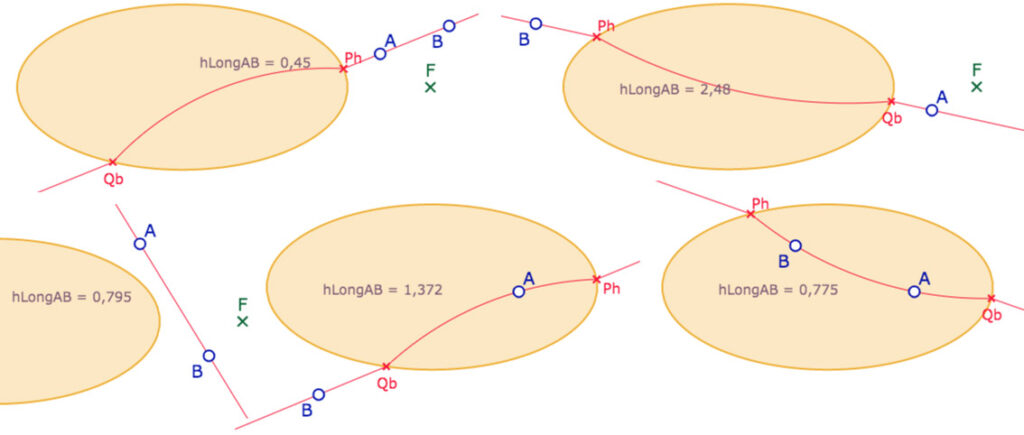
Dans cette macro, on a choisi d’utiliser la pente de la droite quand elle coupe l’ellipse, en particulier pour utiliser moins de points intermédiaires (que dans la macro Milieu ). C’est efficace, on n’utilise que des angles, mais on perd aussi une certaine « commutativité des points ». En effet pour les deux points de coupe, il faut, dans cette macro uniquement, montrer d’abord le point préfixé \(P\) (ou \(p\) selon les figures), celui d’ordonnée la plus grande entre \(P\) et \(Q\), avant de montrer le point \(Q\). C’est pour rappeler cela que dans le nom de la macro les points \(P\) et \(Q\) sont séparés alors que \(A\) et \(B\) sont accolés.
Le détail de la macro-construction Longueur
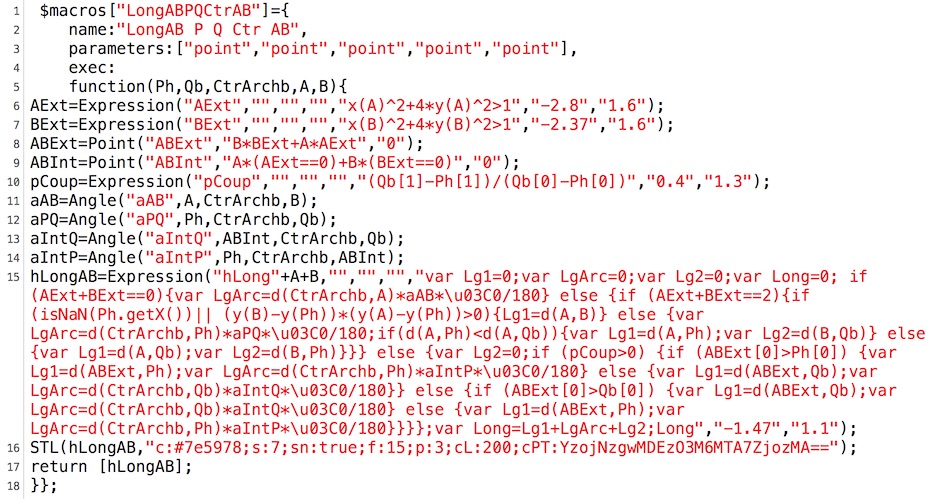
On voit que l’on n’utilise que des angles ou des expressions intermédiaires, mais aucun point. On notera, dans le cas où les deux points sont extérieurs à l’ellipse – les deux illustrations de gauche ci-dessus, l’utilisation explicite de la subtilité des interpréteurs contemporains avec la programmation paresseuse du OU logique en JavaScript dans l’expression
(isNaN(Ph.getX())|| (y(B)-y(Ph))*(y(A)-y(Ph))>0)
En effet la longueur est la distance euclidienne \(d(A,B)\)
• si la droite ne coupe pas l’ellipse (isNaN) ou
• si elle coupe mais que les deux points sont du même côté de l’ellipse (le produit des différences des ordonnées est positif),
ce second cas n’étant exploré par JavaScript que si le premier est faux, donc que si la droite coupe, autrement dit que si le point \(P_h\) existe. S’il n’y avait pas de programmation paresseuse, il y aurait une erreur … mais on aurait fait autrement.
Le milieu de deux points
Pour éviter de devoir montrer \(P\) avant \(Q\) comme dans la macro précédente, on utilise, cette fois plusieurs points intermédiaires. Pour construire le milieu de deux points \(A\) et \(B\), on choisit de réaliser trois points de milieu : \(M_{ii}, M_{ie}\) et \(M_{ee}\) selon que les deux points \(A\) et \(B\) sont respectivement tous les deux intérieurs, un intérieur l’autre extérieur, ou les deux extérieurs à l’ellipse. On rencontre, bien entendu, le même problème que ci-dessus quand les deux sont extérieurs. On utilise la même démarche, ce qui se finalise par le code :
EntreAetB = isNaN(Ph.getX()) || (y(B)-y(Ph))*(y(A)-y(Ph))>0
Alors le milieu final s’écrit
(AExt+BExt==0)?Mii:(AExt+BExt==1)?Mie:EntreAetB?(A+B)/2:Mee
Le point \(M_{ii}\) s’écrit tout simplement, sans objet intermédiaire
Mii = CtrArchb+((A+B)/2-CtrArchb)*d(A,CtrArchb)/d((A+B)/2,CtrArchb)
Pour le point \(M_{ie}\), on construit les points suivants
BordAB est celui où un seul point est extérieur (AExt+BExt==1)
BordAB=Ph(d(ABExt,Ph)(d(abext,ph)>d(ABExt,Qb))
Si ABExt plus loin que la moitié, la moitié est sur le segment [ABExt BordAB], soit
ABExt+(BordAB-ABExt)hLongAB/(2d(ABExt,BordAB))
Quand il est sur l’arc, on considère l’angle suivant
angAB=180(hLongAB/2-d(ABExt,BordAB))/(d(CtrArchb, BordAB)π)
On construit les deux points milT1 et milT2 car le milieu est l’un d’eux selon les orientations de l’arc, et c’est bien entendu celui qui est dans l’ellipse (testé par le booléen milT1int.
milT1= CtrArchb+(BordAB-CtrArchb)(cos(angAB)+isin(angAB))
milT2 = CtrArchb+(BordAB-CtrArchb)(cos(angAB)-isin(angAB))
Mie : (d(BordAB,ABExt)>hLongAB/2)?ABExt+(BordAB-ABExt)hLongAB/(2d(ABExt,BordAB)):(milT1int==1)?milT1:milT2
Enfin, pour le point \(M_{ee}\), on construit les points :
BordA=Ph(d(A,Ph)(d(a,ph)>d(A,Qb))
BordB= Ph(d(B,Ph)(d(b,ph)>d(B,Qb))
dBbord=d(B,BordB)
dAbord=d(A,BordA)
On construit NewEx (nouveau point extérieur), NewBord (nouveau bord), LeExBord (le point d’en face) et longMil (nouvelle longueur)
NewEx = (dAbord<dbbord)?b+(bordb-b)dabord dbbord:a+(borda-a)dbbord= » » dabord= » » Newbord= »(dAbord<dBbord)BordB+(dAbord »>dBbord)BordA
LeExBord = (dAbord<dbbord)borda+(dabord>dBbord)BordB
longMil = arcPQ+d(NewEx,NewBord)
Ensuite on termine par l’angle dans le cas « 2ex »
angExAB =180(longMil)/(d(CtrArchb,NewBord)2π)et les deux points temporaires ( le point final est celui de suffice T1 ou T2)
mil2exT1= CtrArchb+(LeExBord-CtrArchb)(cos(angExAB)+isin(angExAB))
mil2exT2= CtrArchb+(LeExBord-CtrArchb)(cos(angExAB)-i*sin(angExAB))Toujours avec le booléen mil2exT1int qui dit si le point de suffixe T1 est intérieur ou non à l’ellipse.
(d(NewBord,NewEx)>longMil)?NewEx+(NewBord-NewEx)*longMil/(d(NewEx,NewBord)):(mil2exT1int ==1)? mil2exT1: mil2exT2
Exemple de réalisation : les médianes d’un triangle
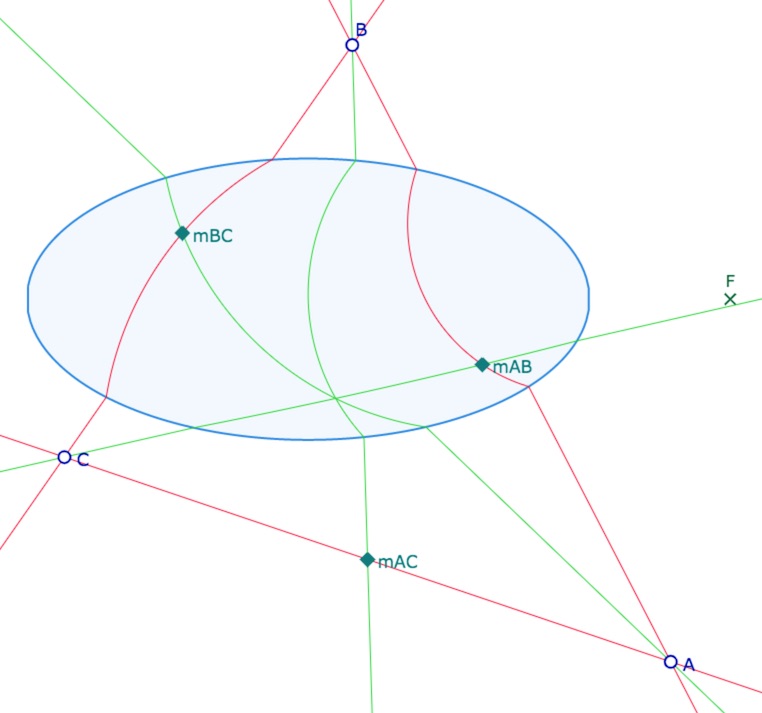
Les médianes ne sont généralement pas concourantes,
mais on peut rencontrer des situations où c’est le cas.
Exemple où deux milieux sont les milieux affines alors que les droites coupent l’ellipse
(avec la gestion dite « paresseuse » du JS … mais en fait hyper pertinente)
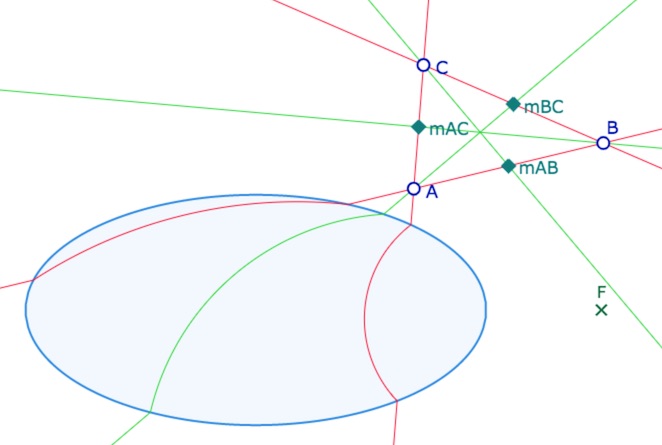
Ouvrir cette figure dans un nouvel onglet pour explorer de nombreuses possibilités