Représentation mentale poétique des épisodes précédents
Les droites remarquables d’un triangle – ce serait vrai aussi pour les bissectrices – sont donc «en pinceau», et elle peuvent l’être dans trois types différents, « à centre », « à axe », ou « sans support ». Lors d’une formation de type « homologie didactique », je résumais en disant que de l’euclidien à l’hyperbolique, on ajoutait un type de pinceau : le type euclidien « parallèle » était scindé en deux, « à axe » et « sans support ». La vraie nouveauté conceptuelle de ce type « sans support » est, pour ces droites, l’aspect non connectables; sans point ni perpendiculaire commune. Une étudiante faisait remarquer que si les droites concourantes sont reliées, au point de concours, par un ruban, alors, en géométrie hyperbolique on peut délier ce ruban, et le tendre ailleurs, les droites remarquables deviennent «à axe», mais on peut aussi perdre le ruban (il n’est pas parti à l’infini, comme le pensait Saccheri) et les droites remarquables deviennent «sans support». Une très belle image.
On va avoir le même phénomène pour les cycles : un cercle est juste un cas particulier où le ruban fait un nœud, nous allons délier le ruban, le tendre pour en faire un axe, mais aussi le perdre. Mais pour faire cela revenons aux fondamentaux. Qu’est-ce qu’un cercle, de manière absolue ?
Le cercle comme image d’un point par un pinceau à centre
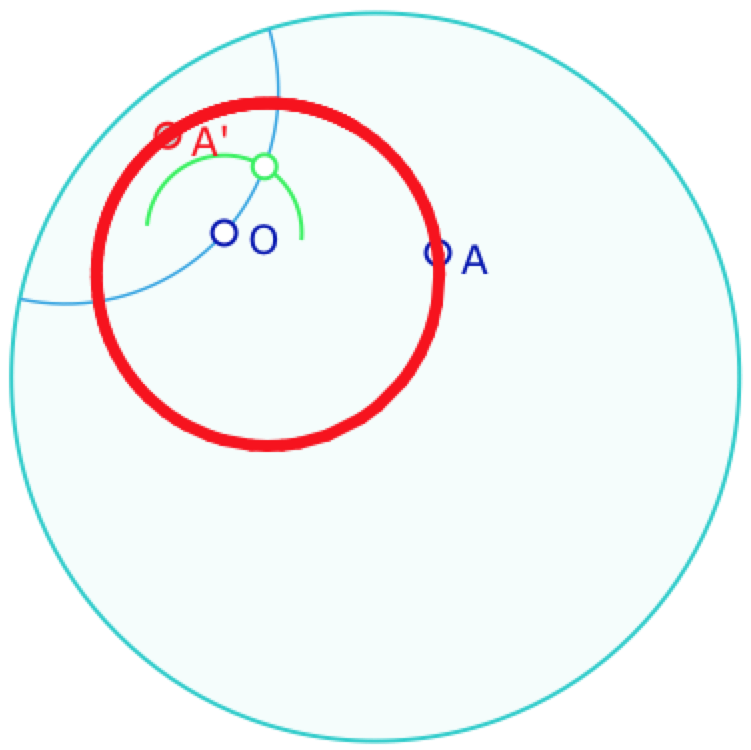
Le cercle de centre \(O\) passant par \(A\) est le lieu des images de \(A\) par les symétries orthogonales d’axes passant par \(O\).
Ci-contre, dans le modèle du disque de Poincaré, il suffit de faire parcourir un point sur un demi-cercle pour faire «le tour des droites» passant par \(O\). On a donc le cercle hyperbolique comme trace de \(A’\) image de \(A\). On voit que c’est un cercle euclidien.
On retiendra que, dans le modèle du disque de Poincaré, le cercle hyperbolique est représenté par un cercle euclidien.
Remarque : on notera surtout le glissement sémantique contenu dans la définition : on est passé de trois droites «en pinceau» à un «pinceau de droites», ce qui n’est pas du tout la même chose, bien entendu. On reste ici dans une approche heuristique. La justification théorique est dans cette page sur la transitivité des pinceaux.
Équidistante d’axe donné passant par un point
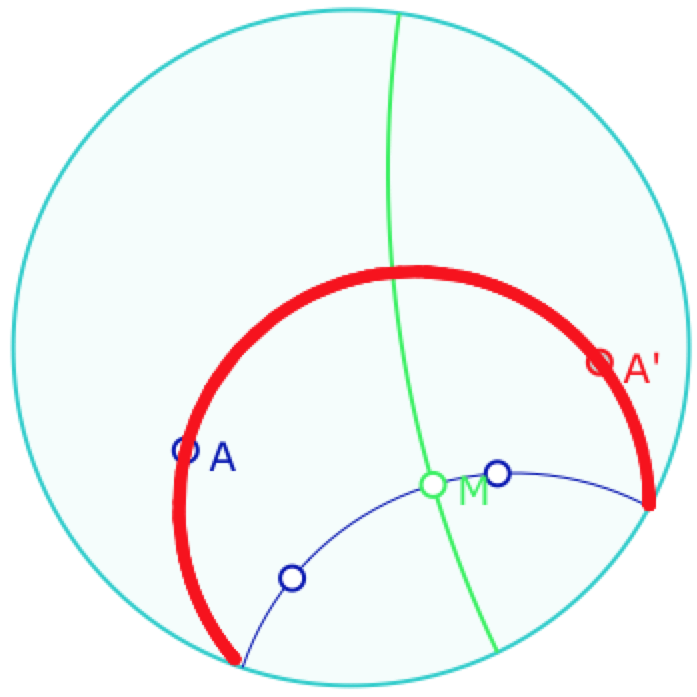
On défait le ruban, cela transforme le pinceau «à centre», qui définit le cercle, en pinceau «à axe» qui va définir un nouvel objet géométrique : le lieu des images \(A’\) d’un point \(A\) par toutes les symétries d’axes orthogonaux à l’axe du pinceau.
Ce lieu a les mêmes points à l’infini que l’axe, ce n’est donc pas un cercle. Par ailleurs on voit (ci- contre – on pourrait le justifier rapidement) que ce n’est pas non plus une droite.
C’est un nouvel objet, appelé une équidistante.
Que l’équidistante hyperbolique ne soit pas une droite a été une grande source d’erreurs historiques sur le V° postulat d’Euclide. Car beaucoup de mathématiciens ont considéré le lieu de l’équidistante d’une droite d’un côté comme étant a priori une droite. Or il s’avère que l’équidistante n’est une droite que dans le cas euclidien.
Dans ce modèle, l’équidistante est un arc de cercle.
Horicycle par centre et point
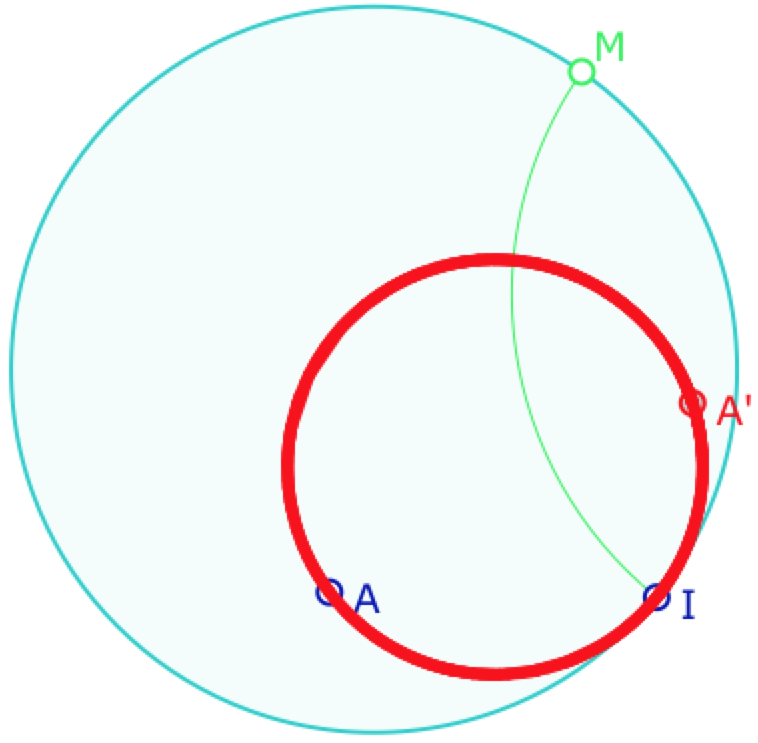
Puis nous perdons le ruban, le pinceau devient «sans support» c’est-à-dire avec un point idéal qui va être le «centre» du nouvel objet : le lieu des images \(A’\) d’un point \(A\) par toutes les symétries orthogonales d’axe passant par le point idéal \(I\). Ce lieu a donc un et un seul point à l’infini, ce n’est donc aucun des objets géométriques précédents. Il est appelé horicycle (horocycle en anglais).
Dans le modèle du disque de Poincaré, un horicycle est représenté par un cercle tangent à l’horizon : c’est le cercle tangent en \(I\) passant par \(A\).
Le cycle de pinceau f passant par un point A
Par pinceau de droites, on entend l’ensemble des droites ayant une propriété donnée, à savoir un point, un axe ou un point idéal. Dans cette démarche heuristique, les propriétés sous-jacentes des pinceaux qui sont utilisées, le sont de manière implicite. Le cycle de pinceau f passant par A est donc un cercle, une équidistante ou un horicycle selon que f soit, à centre, à axe ou sans support.
Figure de synthèse : déplacer les points \(A, B\) ou \(C\) et choisir le type de construction, hauteurs ou médiatrices.
Préférer ouvrir cette figure dans un nouvel onglet.
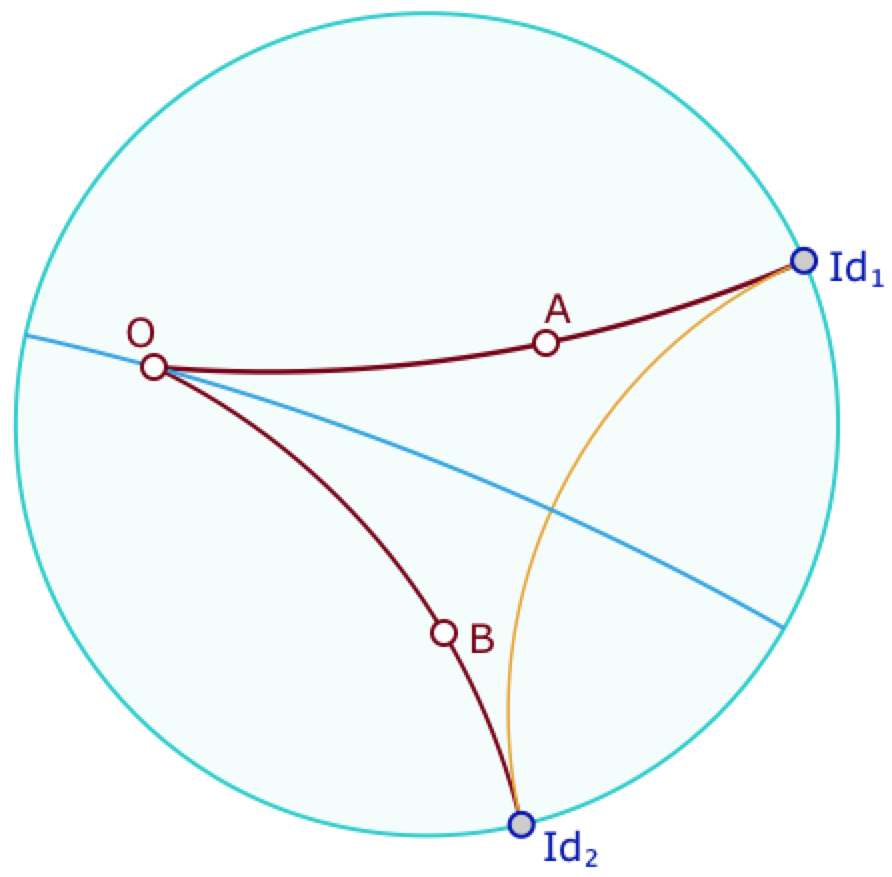
Exemple d’application : le cercle inscrit et les cycles exinscrits
Dans un premier temps, on peut construire la bissectrice de l’angle \(AOB\) comme hauteur issue de \(O\) du triangle idéal associé. En effet un triangle idéal a ses côtés de «longueurs infinies », donc égales. Plus sérieusement, le principe est que, dans ce contexte, la hauteur est aussi axe de symétrie (il faudrait préciser bien entendu ce que c’est), et donc bissectrice de l’angle au sommet.
On notera que c’est clairement une construction «dans le modèle» car on utilise explicitement l’usage des points idéaux.
Avec des macros cercle, équidistante on peut construire une figure générale avec les bissectrices, le cercle inscrit et les cycles exinscrits.
Dans une telle figure, la macro d’horicycle n’est pas utilisable, car on n’accède pas à un horicycle en manipulation directe à la souris.
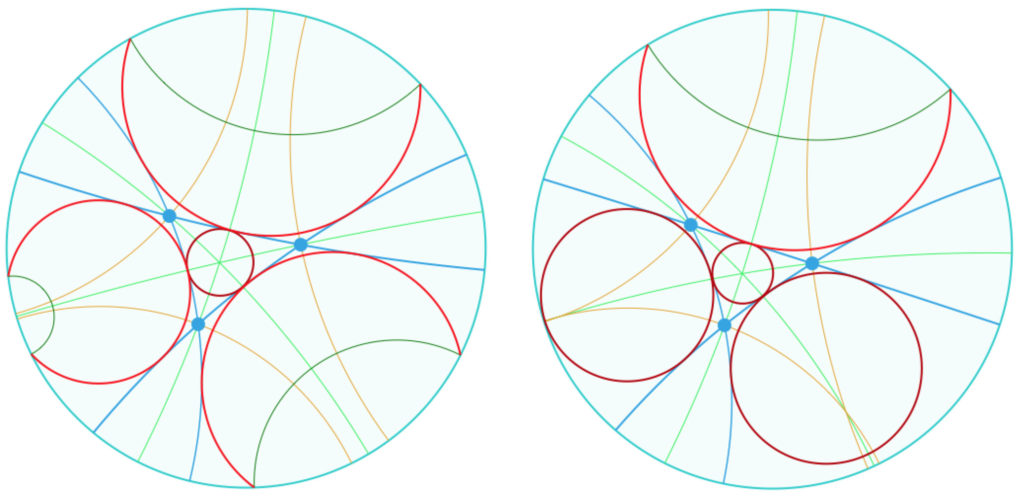
Préférer ouvrir cette figure dans un nouvel onglet
Retour sur la figure de Malfatti
Il n’y a aucune difficulté à faire la figure de Malfatti comme décrite dans cette page sur la géométrie euclidienne bornée.
Par contre, on voit bien que l’on ne peut pas avoir accès au «centre du cercle exinscrit» quand il n’y a pas de cercle et il s’agit d’une équidistante.
On imagine bien que la situation accepte une généralisation, non seulement théorique, mais aussi constructive. C’est ce que nous verrons dans l’item des trilatères.
Préférer ouvrir cette figure dans un nouvel onglet.
Exemples de constructions autour des parallèles ou des horicycles

Triangles ayant leurs hauteurs parallèles
Soit \(H\) un point idéal, un point du cercle horizon, et deux droites \((HA)\) et \((HA)\) . On cherche à construire un point \(C\) tel que les hauteurs du triangle \(ABC\) soient parallèles avec comme point idéal le point \(H\).
On travaille dans un modèle dans lequel les points idéaux sont accessibles, ce qui simplifie fortement les constructions.
Si \((BH)\) est une hauteur, alors \(C\) est sur la perpendiculaire à \((BH)\) passant par \(A\). \(C\) est aussi sur la perpendiculaire à \((AH)\) passant par \(B\). Si ces deux droites sont sécantes, l’intersection est le troisième sommet \(C\).
Puisque l’on sait que les hauteurs sont en pinceau, la droite \((HC)\) est nécessairement la troisième hauteur du triangle \(ABC\).
Le point \(C\) peut ne pas exister, on est alors dans une configuration où il n’y a pas de triangle solution.
Triangle orthique d’un triangle idéal
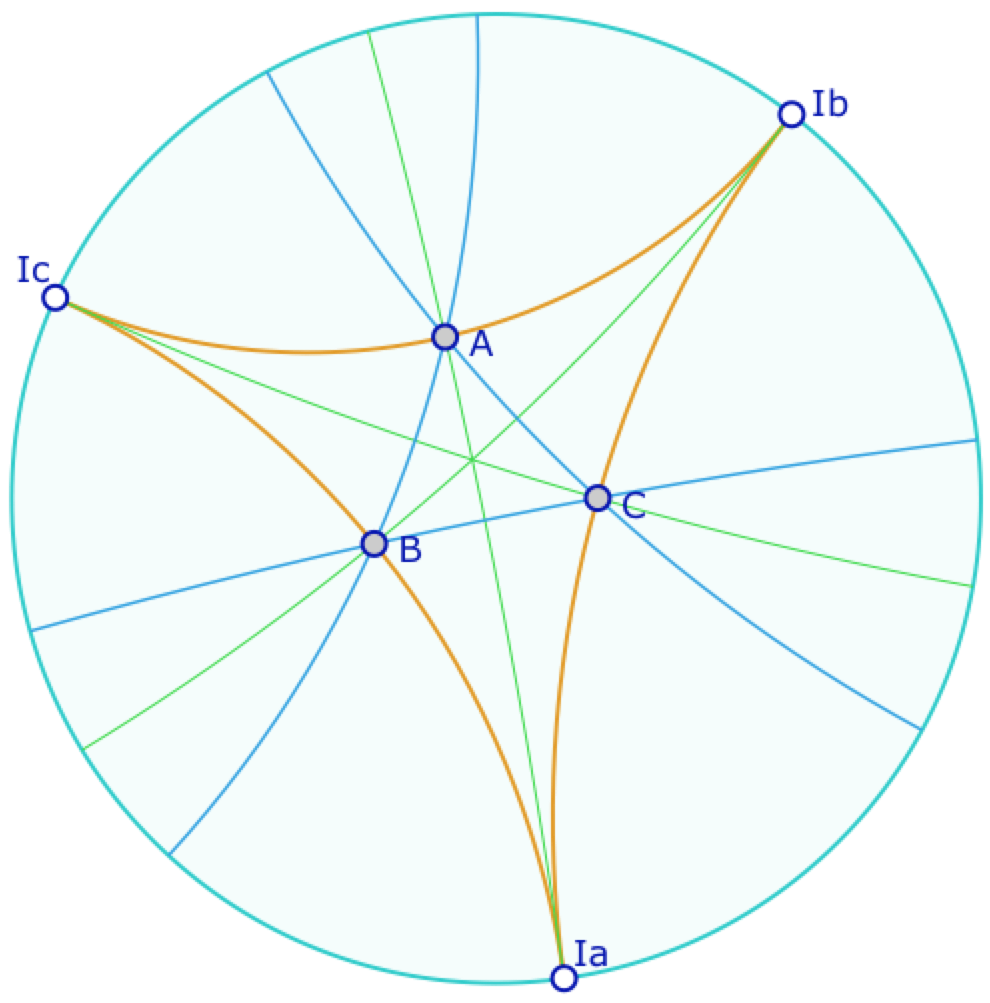
Soient \(I_a, I_b, I_c\)trois points idéaux. Soit d’abord \(B\) le pied de la hauteur issue de \(I_b\) du triangle idéal. Cette hauteur, comme droite hyperbolique est axe de symétrie du plan hyperbolique. La droite étant perpendiculaire à \((I_aI_c)\), les deux points \(I_a\) et \(I_c\) sont symétriques par rapport à \((BI_b)\). Autrement dit la hauteur est aussi bissectrice du triangle.
On fait de même avec les autres pieds des hauteurs \(A\) et \(C\). Alors le symétrique de \(A\) est un point \(M\) de \((I_bI_a)\) tel que \((MI_c)\) soit orthogonal à \((I_bI_c)\) car la symétrie orthogonale d’axe \((BI_b)\) conserve l’orthogonalité.
Et donc \(M=C\).
Autrement dit \((BI_b)\) est aussi orthogonale à \((AC)\) . Cela signifie d’une part que \((BI_b)\) est la perpendiculaire commune à \((AC)\) et \((I_aI_c)\), mais aussi que le triangle \(ABC\) est isocèle en \(B\) et donc équilatéral car on peut faire ce raisonnement pour chaque hauteur. Les hauteurs du triangle idéal sont aussi les hauteurs et les bissectrices de son triangle orthique (triangle des pieds des hauteurs) équilatéral. Là encore, c’est une propriété absolue, dont la preuve est proposée dans cette page.
Leur intersection est aussi centre du cercle inscrit du triangle orthique \(ABC\). On le montre dans un contexte plus général de géométrie absolue (Théorème 25 de cette page).
Construction d’un triangle dont les cycles exinscrits sont trois horicycles
Cette figure peut avoir une autre interprétation. En effet, \(I_a, I_b\) et \(I_c\) étant donnés initialement, le triangle orthique \(ABC\) admet comme bissectrices intérieures les droites \((XI_x)\) pour \(X \in \{A, B, C \}\)et les droites initiales comme bissectrices extérieures.
Autrement dit les points idéaux sont les centres des horicycles exinscrits de \(ABC\). On vient ainsi de montrer que :
Le triangle orthique d’un triangle idéal est équilatéral et admet comme cycles exinscrits les horicycles de centres les points idéaux et passant par les milieux des côtés.
Ils sont tangents en ces milieux au cercle inscrit … qui est aussi le cercle d’Euler.
Ci-dessous déplacer simplement les points idéaux.
Préférer ouvrir cette figure dans un nouvel onglet.
Des propriétés métriques remarquables de cette figure sont présentées dans cette page du modèle KB et sont démontrées dans cet article.
Utilisation des deux horicycles passant par deux points
En rouge les deux horicycles passant par \(A\) et \(B\). Les centres des deux horicycles sont les points idéaux de la médiatrice de \([AB]\). On s’intéresse à caractériser, à partir de ces deux horicycles, l’ensemble des points \(C\), tels que les trois médiatrices du triangle \(ABC\) ne sont pas concourantes.
\(A\) et \(B\) étant donnés, on chercher à caractériser la région des points \(C\) tels que \(ABC\) n’a pas de cercle circonscrit.
Préférer ouvrir cette figure dans un nouvel onglet
Réponse : on trouvera que les médiatrices sont concourantes dans la différence symétrique des intérieurs des deux horicycles. Et donc l’ensemble des points \(C\) tels que les médiatrices ne sont pas concourantes et le complément de la différence symétrique de l’intérieur des horicycles.