Si toute droite elliptique admet un pôle, son «pôle nord sur la sphère», réciproquement tout point \(P\) du plan elliptique admet une polaire, la droite elliptique correspondant à l’équateur du point \(M\) associé sur la sphère.
Par définition, la polaire d’un point \(P\) est la droite dont \(P\) est le pôle, c’est donc la droite qui est perpendiculaire à toute droite passant par \(P\). Cette droite existe, c’est simplement la perpendiculaire commune à deux droites passant par \(P\).
Quand une droite est un cercle particulier
Reprenons notre définition absolue d’un cercle, à savoir l’image d’un point par un faisceau à centre. On anticipe un peu, en supposant connue la symétrie orthogonale : elle existe sur la sphère, il suffit de la transposer par antipodie elliptique, nous le ferons un peu plus loin.
Soit alors un point \(O\), et \(A\) un point de sa polaire. L’image de \(A\) par le faisceau à centre \(O\) (donc le cercle de centre \(O\) passant par \(A\) est contenu dans la polaire de \(A\), qui est une droite invariante par les symétrie orthogonales d’axes passant par \(O\). Par ailleurs il est facile d’imaginer que pour deux points \(A\) et \(B\) de la polaire il existe une symétrie orthogonale d’axe passant par \(O\) envoyant \(A\) sur \(B\) : sur la sphère il suffirait de prendre la bissectrice de l’angle sphérique \(\angle AOB\) en \(O\), ce que l’on sait calculer – dans le cadre de «la sphérique» depuis bien longtemps. Et donc finalement l’image de \(A\) par le faisceau à centre \(O\) est la polaire elle-même.
Ainsi, toute droite est un cercle de centre son pôle.
On est très éloigné de nos représentations géométriques usuelles, pour de nombreuses raisons mais en particulier celle-ci dont la négation est régulièrement utilisée dans le contexte euclidien : en géométrie elliptique, trois points alignés sont toujours sur un même cercle. Bien entendu il existe de «vrais» cercles, qui ne sont pas des droites, mais il va falloir être vigilant pour parler de cocyclicité hors de l’alignement. On touche là, une des difficultés de l’axiomatisation générale de la géométrie absolue, pour qu’elle contienne aussi la géométrie elliptique : les propriétés elliptiques sont si générales qu’il faut être vigilant dans les argumentations. Par exemple ici on ne peut plus utiliser l’argument de non alignement de trois points sur un cercle dans une preuve comme on l’a parfois dans des contextes euclidiens ou hyperboliques.
Vers une analyse métrique … et ses conséquences.
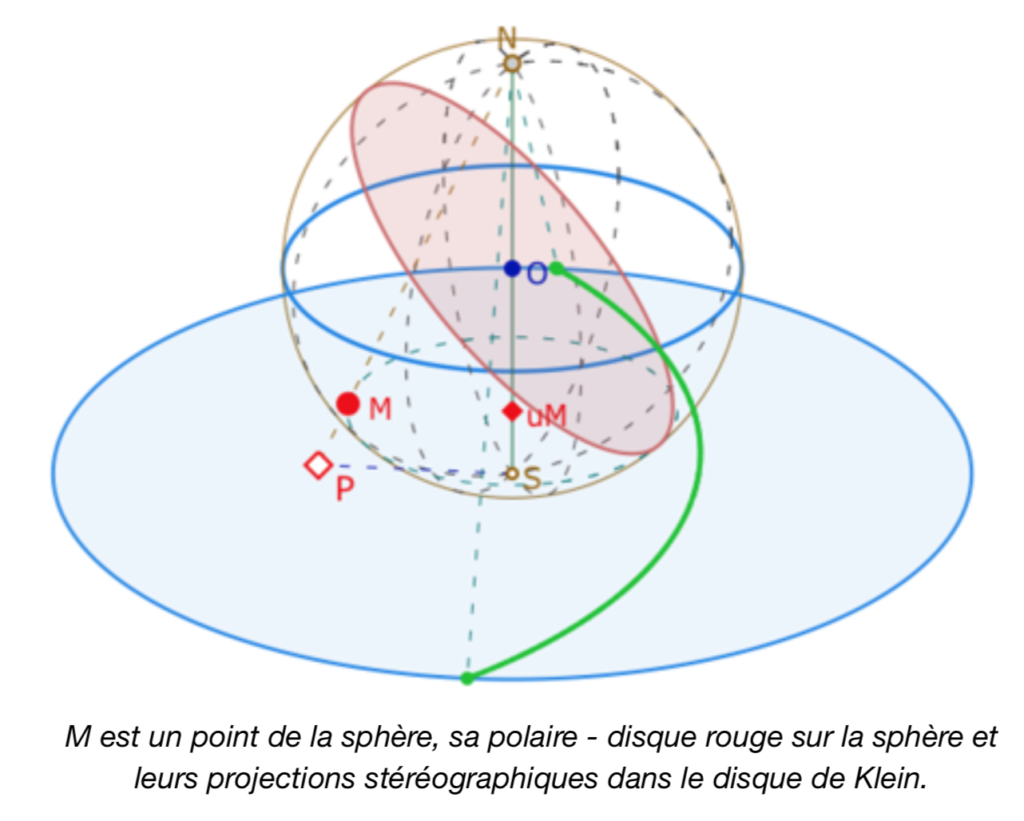
Revenons sur la représentation avec la sphère. Pour le point \(M\) de la sphère, associé au point elliptique \(P\), la polaire de \(P\) est l’équateur associé \(M\) étant le «pôle nord»). Mais c’est aussi, d’une certaine façon, son horizon, dans un sens physique, puisque les points au delà de la demi-sphère définie par cet équateur ne son pas visibles physiquement, mais aussi d’un point de vue mathématique, car les points «au delà» de l’horizon n’existent pas, ils sont elliptiquement identifiés à un point de l’hémisphère contenant \(M\).
Sur la sphère, l’équateur associé à \(M\) est donc aussi l’ensemble des points (de la demi-sphère) les plus éloignés de \(M\), et tous à même distance par conservation de l’équateur par toute symétrie orthogonale passant par le pôle \(N\). On retrouve donc un aspect métrique de «même distance» entre deux points \(A\) et \(B\) de la polaire avec le centre \(O\). S’il existe une distance elliptique, avant même de la connaitre, elle confirme que la polaire d’un point \(O\) est un lieu des points à même distance de \(O\), et c’est précisément le lieu des points à la distance maximale possible dans le cas elliptique.
Comme par construction, c’est la moitié d’une droite elliptique, cette première analyse montre – et Saccheri l’avait déjà vu dès le XVIII°s – que la géométrie elliptique est métriquement bornée.
Remarque sur l’interface : comme tous les cercles sont des ellipses en 3D et que l’objet arc d’ellipse n’existe pas dans le logiciel, on ne peut pas (du moins pas immédiatement) faire un arc d’ellipse initial, sur la partie rouge, pour ensuite en faire un lieu (partie verte). On peut faire un arc d’ellipse à partir d’un arc de cercle, mais pas à partir d’un arc d’ellipse.
Le point \(M\) se manipule par sa côte \(u_M\) puis sur son parallèle à l’équateur. La polaire de \(P\) est la partie de l’arc vert à l’intérieur du disque.
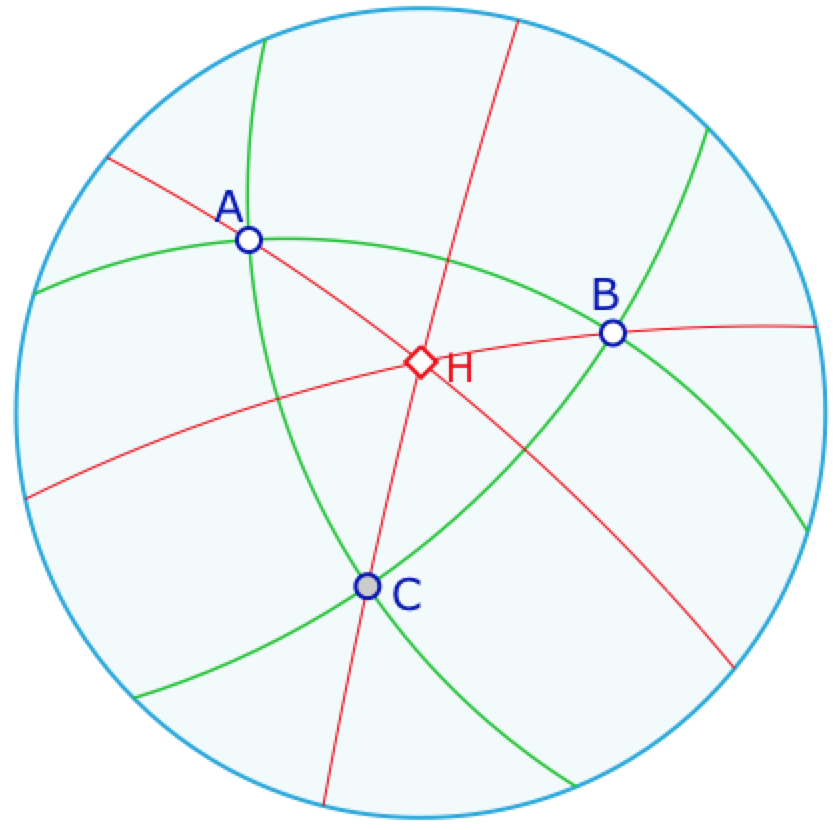
Triangle tripolaire et orthocentre
Sur la sphère, il est immédiat de construire un triangle avec trois angles droits : depuis le pôle nord \(N\) on construit deux droites orthogonales. Ces droites coupent l’équateur en deux points \(A\) et \(B\). Alors le triangle \(NAB\) est un triangle qui a trois angles droits et pour lequel chaque sommet est pôle de la droite opposée, et donc chaque droite polaire du sommet opposé : le triangle est appelé triangle tripolaire.
Dans ce cas, tout point n’appartenant pas à l’une des trois droites associées au triangle est l’intersection de trois hauteurs du triangle : ce triangle a donc une infinité d’orthocentres.
Ce triangle tripolaire est aussi un triangle équilatéral, chaque côté ayant pour longueur la moitié de la longueur d’une droite (chaque pôle centre du cercle-polaire).
Demi-droite
On a déjà présenté la polaire d’un point comme « la droite de l’horizon » pour son pôle. C’est aussi un cercle de centre \(O\), et donc pour tout point \(A\) de la polaire de \(O\), le (faux) « segment » \([AA]\) de centre \(O\), est toute la droite \((OA)\). Étant donnés deux points \(A\) et \(B\), on peut définir la demi droite [AB) comme la partie de la droite \((AB)\) qui va de \(A\) à sa polaire, en passant par \(B\). Une demi-droite est aussi la moitié d’une droite.
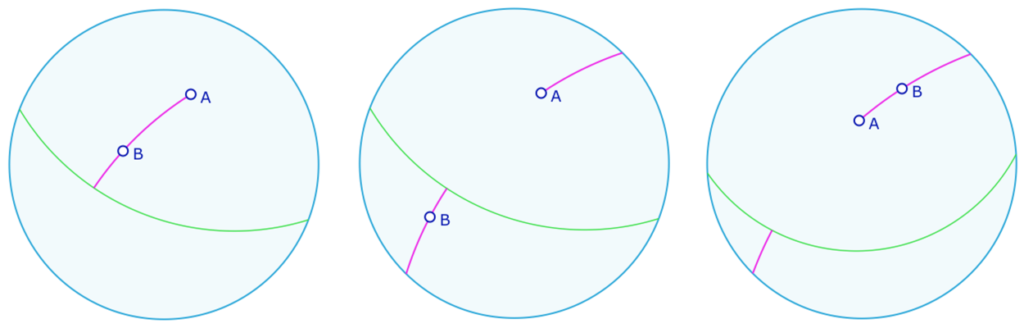
Les trois configurations du modèle correspondent à deux cas : si la demi droite reste dans la même partie que latex]A[/latex] ou non.
Un environnement non isotrope : avec ce point de vue sur la polaire comme, d’un certain point de vue « droite de l’infini » (à distance bornée) propre à son pôle, on peut se souvenir de ce que disait de Riemann autour de ce sujet :
« Outre cette propriété des segments superficiels d’être indépendants du lieu, la surface de mesure de courbure nulle possède encore la propriété que la direction est indépendante du lieu, propriété qui n’existe pas chez les autres surfaces »
« Hypothèses qui servent de fondement à la géométrie » – Riemann – p 293
La polaire comme «droite de l’infini» de son pôle
Exploration de la figure – différentes macro-constructions elliptiques disponibles.