Dans cette page on poursuit l’exploration du régionnement du plan, on s’intéresse à la situation 1H1E soit la région du plan d’où on peut mener à la fois une – et un seule – perpendiculaire hilbertienne et une perpendiculaire euclidienne.
On se propose ici essentiellement d’illustrer ce que l’on peut explorer avec la figure dynamique proposée en fin de page. Les détails techniques de réalisation sont proposés dans cette page de blog.
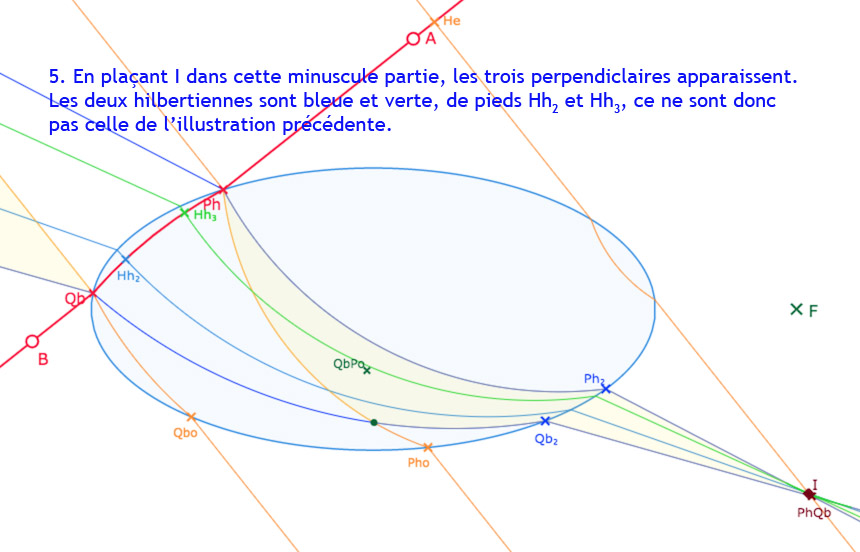
La région 1H1E, jaune dans les illustrations, est généralement composées de 4 parties, deux issues des intersections de la droite \((AB)\) avec l’ellipse, soit les points \(Ph\) et\(Qb\) et deux autres issues des points \(QbPo, PhQo\) ou \(PhQb\), ces parties pouvant parfois être en dehors de l’écran, ou tout simplement ne pas exister.
Le point \(PhQo\) est l’intersection des deux droites affines \((Ph \, Ph_2)\) et \((Qb \, Qbo)\), \(QbPo\), celle des droites affines \((Qb \, Qb_2)\) et \((Ph \, Pho)\). Enfin le point \(PhQb\), elle celle des droites affines \((Ph \, Ph_2)\) et \((Qb \, Qb_2)\). Ainsi, par exemple, les H-droites \((Ph \, QbPo)\) et \((Qb \, PhQo)\) sont-elles parallèles car toutes deux orthogonales (euclidiennement) à la droite \((AB)\).
Dans la figure dynamique proposée, on peut manipuler un point \(I\) d’où l’on trace les perpendiculaires à la droite \((AB)\), ce qui permet d’illustrer qu’il y a bien deux perpendiculaires issues de \(I\), et de types différents.
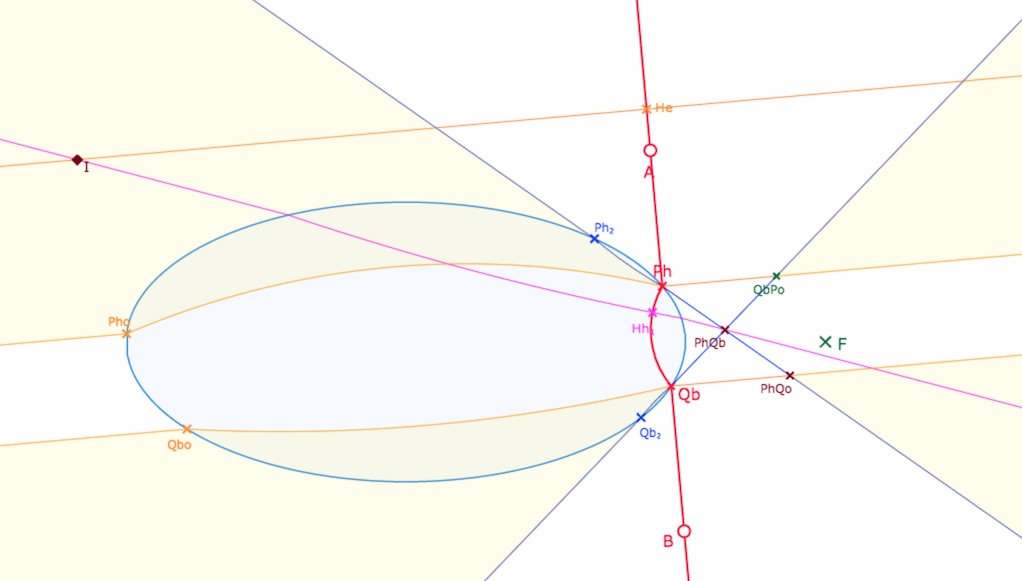
Configuration un peu générique de la situation 1H1E avec 4 parties
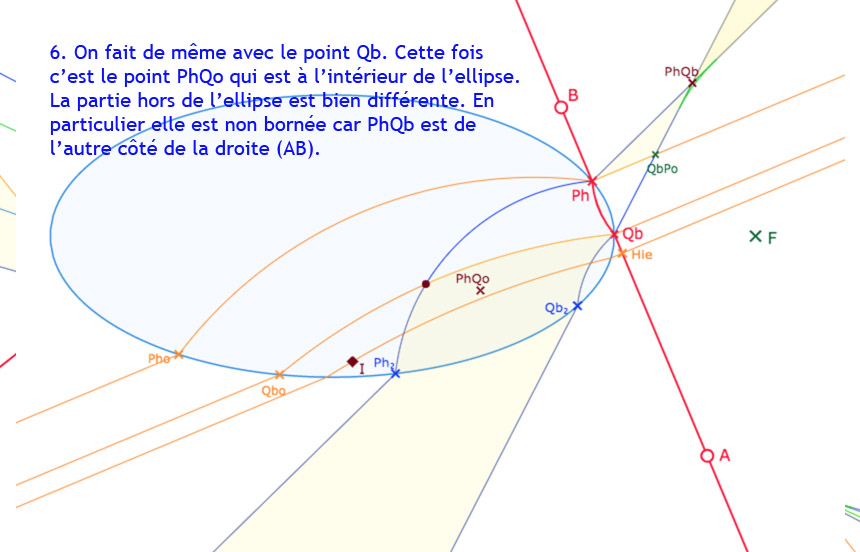
Les parties issues des points d’intersection avec l’ellipse peuvent être, elles aussi, des triangles ou des quadrilatères, quand elles sont extérieures à l’ellipse et comportent, en général, un ou deux arcs de cercles – comme ci-dessus – quand elles ont une partie à l’intérieur de l’ellipse.
On rappelle que la partie rose est celle d’où l’on peut mener deux perpendiculaires hilbertiennes, et la partie verte, celle d’où l’on peut mener deux hilbertiennes et une euclidienne.
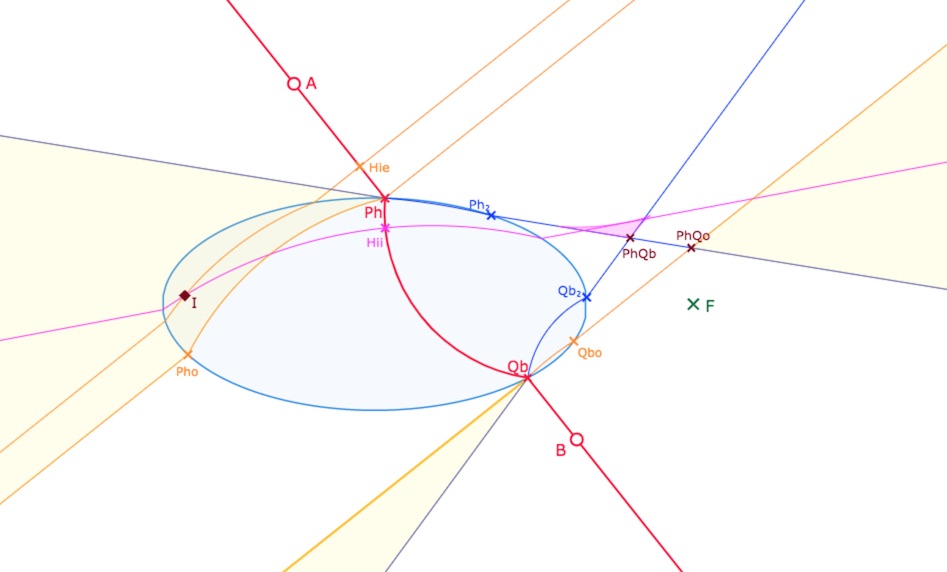
La partie issue de \(Ph\) comporte un seul arc, celle de \(Qb\) est un triangle extérieur.
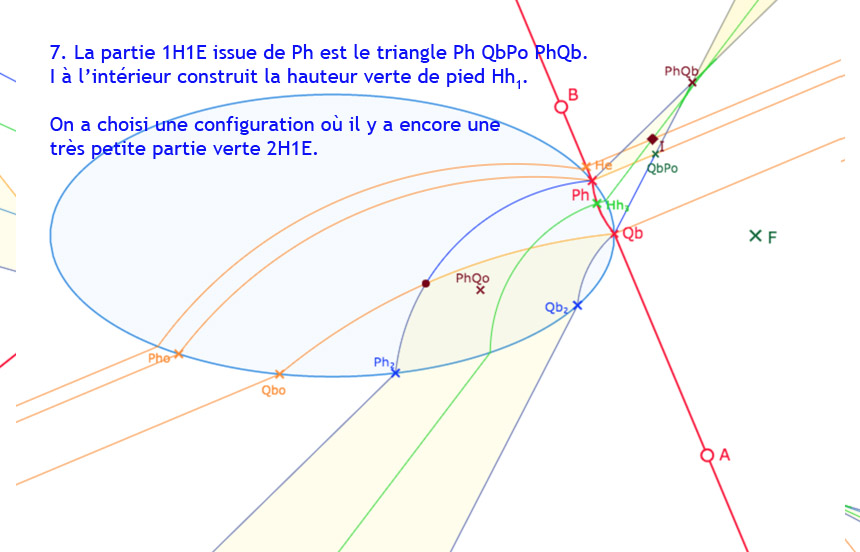
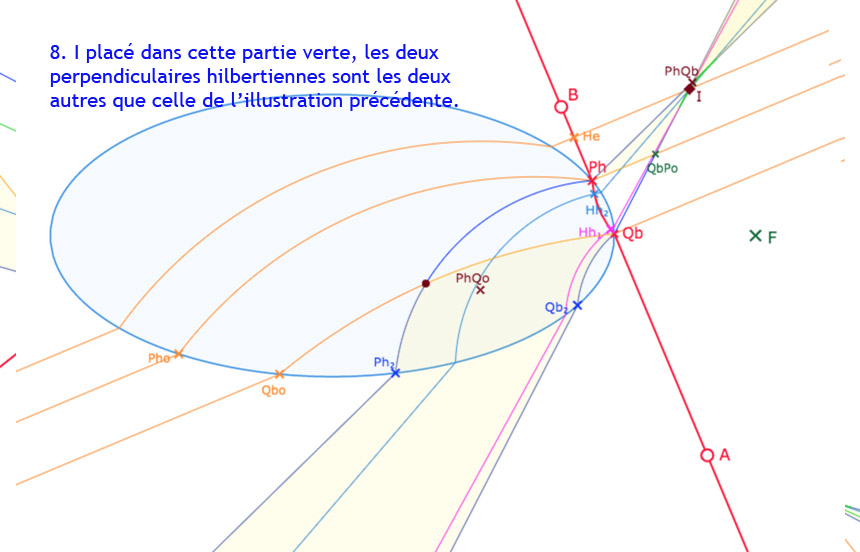
On notera que les noms des pieds des hauteurs changent selon la configuration. Dans les deux illustrations, \(I\) est dans la même partie issue de \(Ph\), mais dans la première \(I\) est extérieur à l’ellipse, et à l’intérieur dans la seconde. Or on a vu, dans cette page technique, que les constructions sont différentes selon la position du point \(I\) : il y a potentiellement 7 constructions de perpendiculaires possibles – dont 4 peuvent exister simultanément, et donc 7 noms de pied de perpendiculaire différents.
Enfin, quand les parties rose ou verte contiennent un point de rebroussement, on a aussi vu, cette fois de manière empirique, qu’au voisinage de ce point, il peut y avoir non pas deux, mais trois perpendiculaires hilbertienne comme illustré ci-dessous.
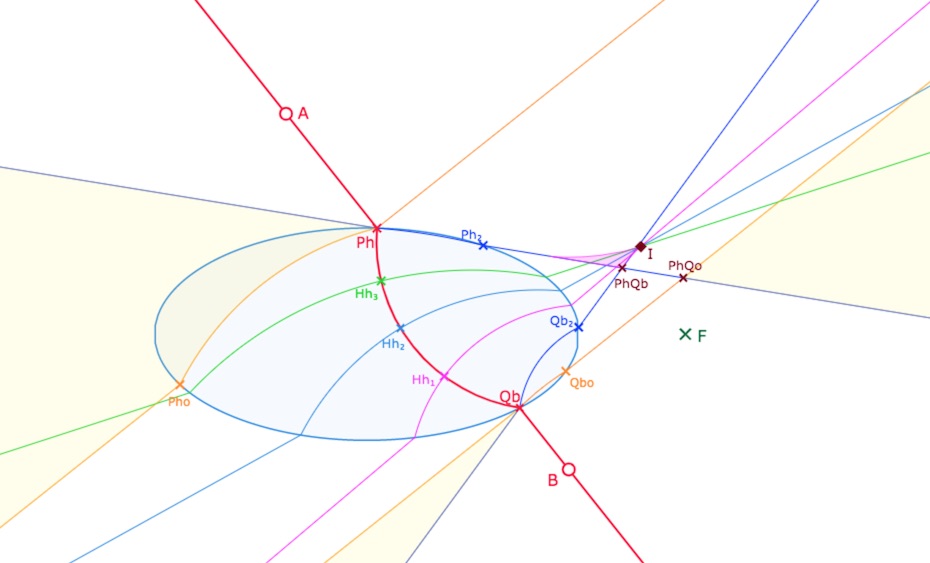
Cas où les parties issues de Ph ou Qb
comportent trois arcs de cercles
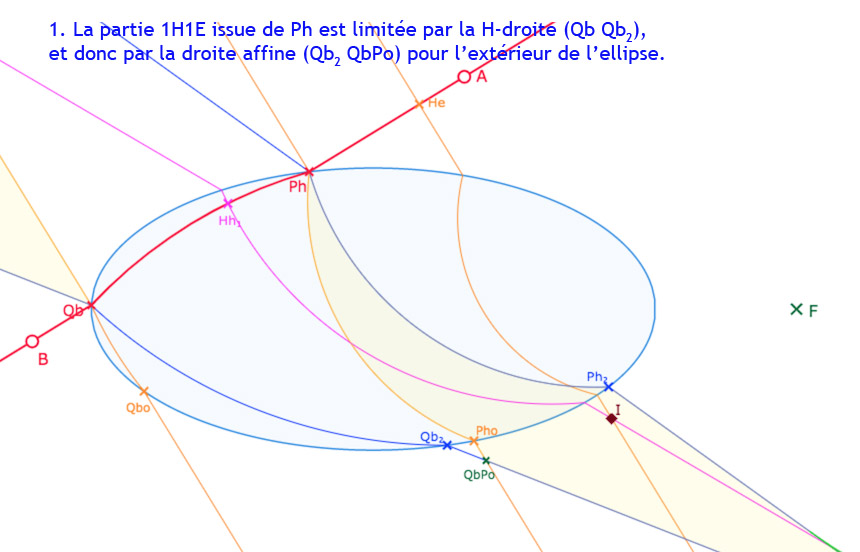
Partons d’une autre forme de la partie 1H1E issue de \(Ph\), où intervient le point \(QbPo\). La partie extérieure à l’ellipse est tronquée, à partir de \(QbPo\) par la droite \((Qb \, Qb_2\). On note le début d’une large partie 2H1E, la partie verte.
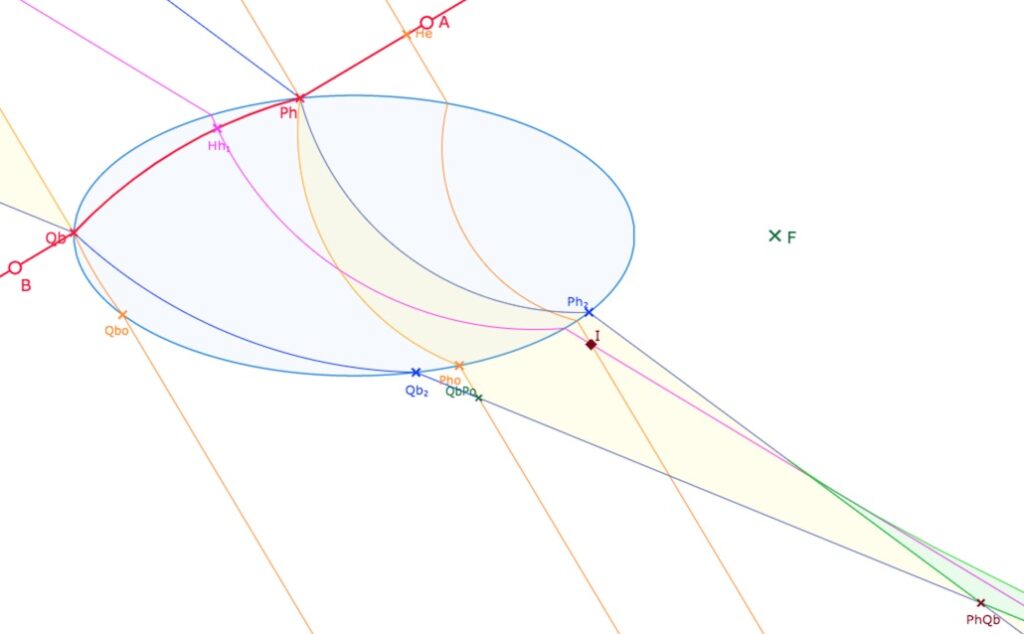
Prélude à une partie intérieure à l’ellipse composée de trois arcs de cercle
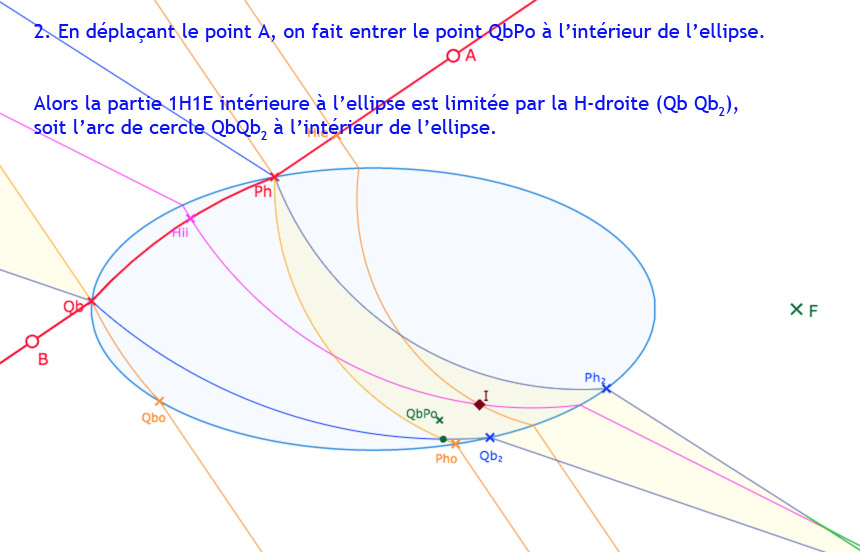
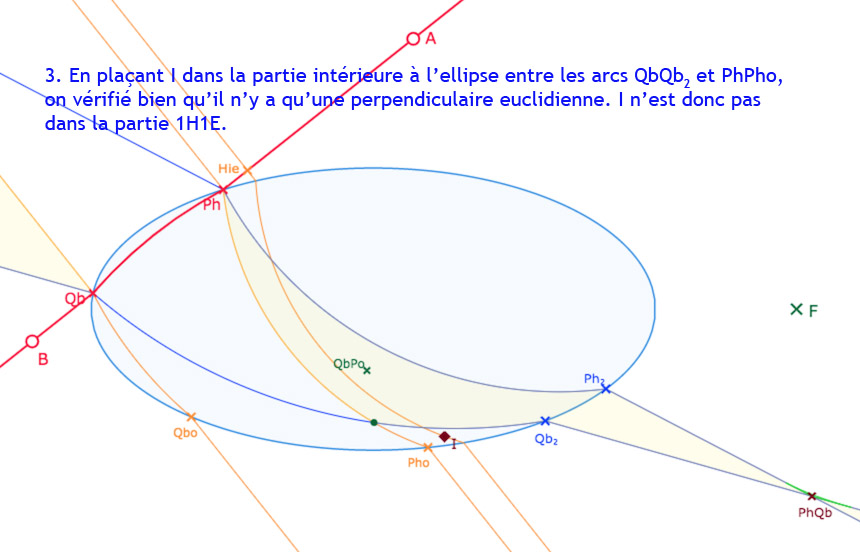
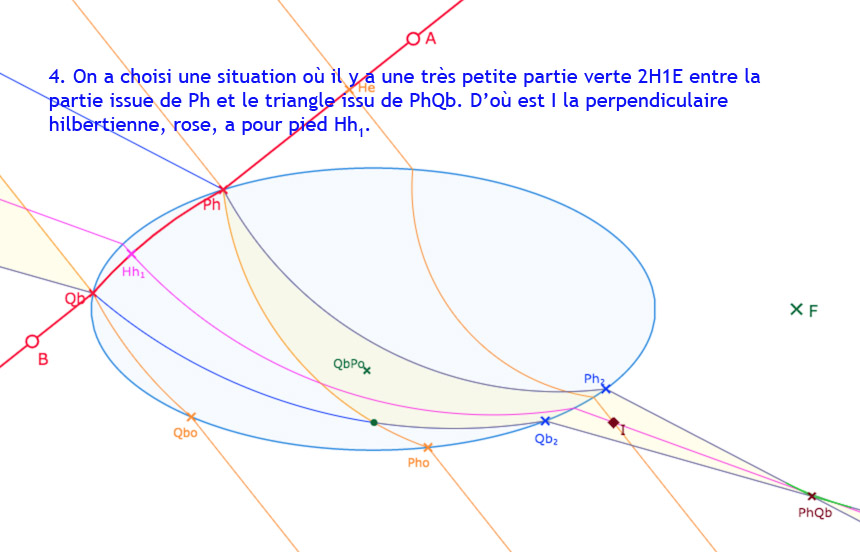
En déplaçant le point \(A\), on va faire entrer le point \(QbPo\) à l’intérieur de l’ellipse, et la partie de 1H1E à l’intérieur de l’ellipse va être tronquée par l’arc de cercle \(QbQb_2\). C’est très clair en faisant la manipulation – proposée plus loin dans la page – mais voici quelques illustrations commentées dans la galerie suivante
Galerie de 8 illustrations pour rendre compte des parties ayant 3 arcs de cercles
Quelques configurations standards ou particulières
(proposées pour être explorées)
Cas où les 4 parties sont des triangles non bornés
Il suffit de placer la droite \((AB)\) dans une position proche de la verticale et à gauche de l’origine du repère \(Ie\) pour être dans cette configuration car les deux arcs de cercles en chaque point d’intersection vont vers le point \(F\) et ne remplissent pas les critères pour faire partie de 1H1E (consulter la page de présentation technique pour plus de détails)
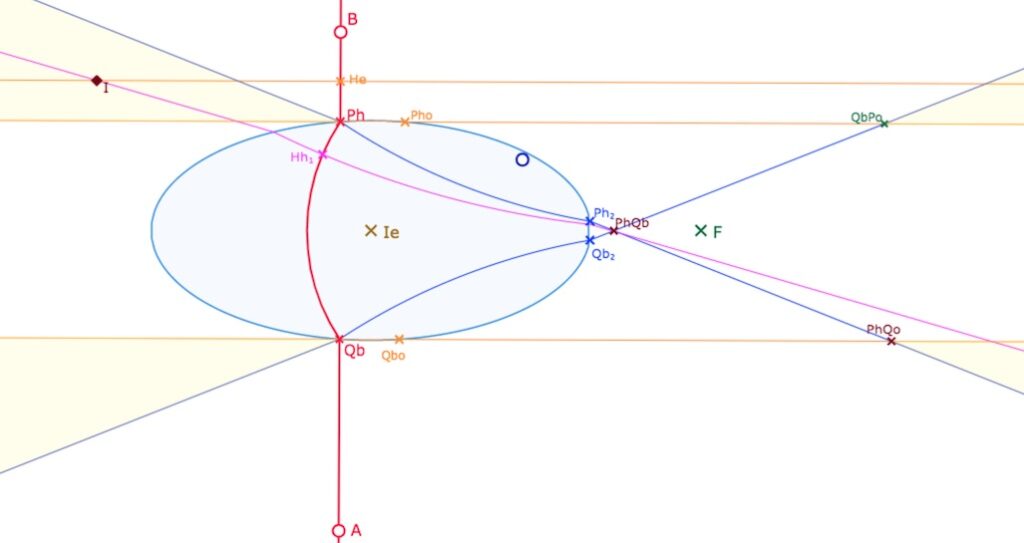
Les arcs issus de \(Ph\) et\(Qb\) sont tous deux incurvés en sens inverse
C’est juste une configuration pour l’esthétique, sans aucun sens mathématique. Pour des raisons élémentaires, il suffit que la droite \((AB)\) coupe l’ellipse proche du sommet du côté de \(F\)
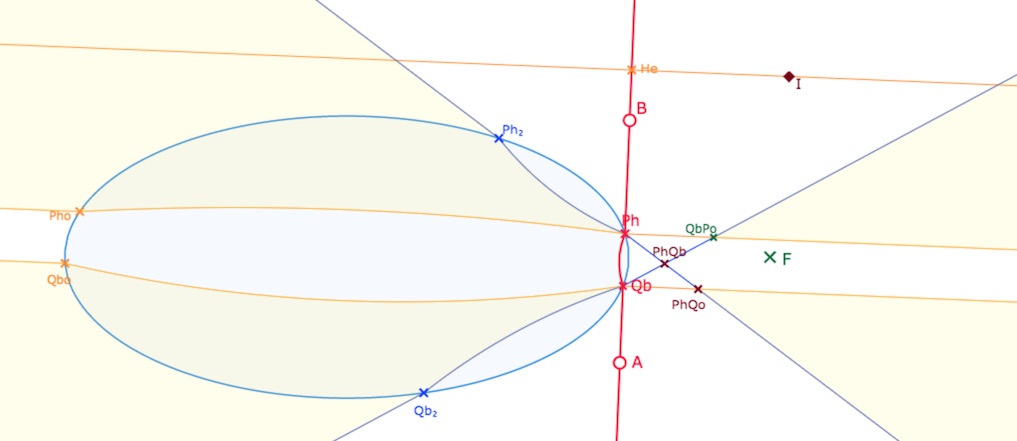
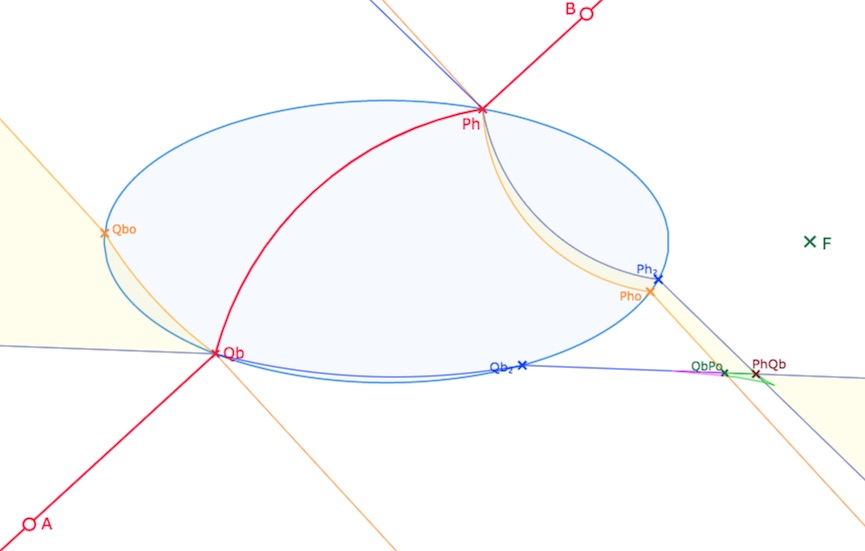
Une configuration où la partie 2H1E a une pointe dans 1H1E
Cette configuration est plus originale, et nécessite un peu de précision pour être reproduites. Comme le point de rebroussement est dans 1H1E cela signifie qu’en plaçant \(I\) proche de ce point, il y aura 4 perpendiculaires à \((AB)\), trois hilbertiennes et une euclidiienne.
La figure dynamique
Dans cette figure, déplacer les points \(A, B\) et \(I\).
Préférer utiliser une figure hors site plus grande. Elle s’ouvre dans un nouvel onglet.