Cette page suppose que le lecteur connaisse les notions d’équidistante et d’horicycle. Si nécessaire, on peut lire les présentations qui ont été faites dans le modèle du disque de Poincaré.
Pour ces deux cycles, l’utilisation des calculs réalisés autour de l’orthogonalité va nous permettre de revenir à des constructions basées sur des considérations géométriques. En effet, l’équidistante à une droite \(d\) passant par un point \(M\) est le lieu de l’image de ce point par toutes les droites orthogonales à \(d\). Une première macro-construction donnant le pied de la perpendiculaire, une seconde, la symétrie centrale d’un point par rapport à ce pied, permet, en quelques objets, de construire l’image de ce point \(M\).
Un mot sur les macros utilisées
Ce retour à « la géométrie » est l’occasion de parler de la façon dont sont réalisées ces figures Seules quelques macros sont des macros de « dessins » à l’écran. On place un point, on trace un segment ou une droite, ou encore un cercle. Toutes les autres macros – et elles sont nombreuses – sont des constructions d’expressions, soit de coordonnées, soit de constantes de droites : ces macros n’ont que quelques objets intermédiaires.
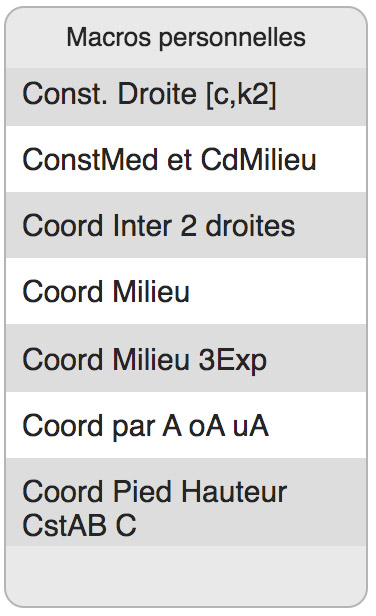
Dans ce micro-monde, on jongle surtout avec les coordonnées d’objets. Ci-contre en voici quelques unes pour se faire une idée.
Const. Droite [c,k2], donne, depuis les coordonnées de 2 points \(A\) et \(B\), les constantes de la droite \((AB)\).
ConstMed et CdMilieu : à partir des coordonnées de deux points, renvoie les constantes de la médiatrice, et les coordonnées du milieu.
Coord Milieu, Cord Milieu 3 exp : les coordonnées du milieu à partir soit de deux points (coord) ou de 3 données (en ajoutant comme donnée les constantes de la droite).
Coord par A, oA, uA : renvoie les cordonnées [latitude \(u_A\), longitude \(\theta_A\)]
Coord Pied Hauteur par CstAB C : il suffit d’avoir les constantes de la droite \((AB)\) et les coordonnées de \(C\) pour avoir les coordonnées du pied de la hauteur.
On l’aura compris, l’essentiel est un travail de coordonnées avant de construire les figures finales par quelques macros de dessin. C’est très efficace, et permet de réaliser des figures assez riches qui restent manipulables.
La symétrie orthogonale
C’est la simple composition du pied de la hauteur et de la symétrie centrale. En voici un résumé illustré
(copie d’écran).
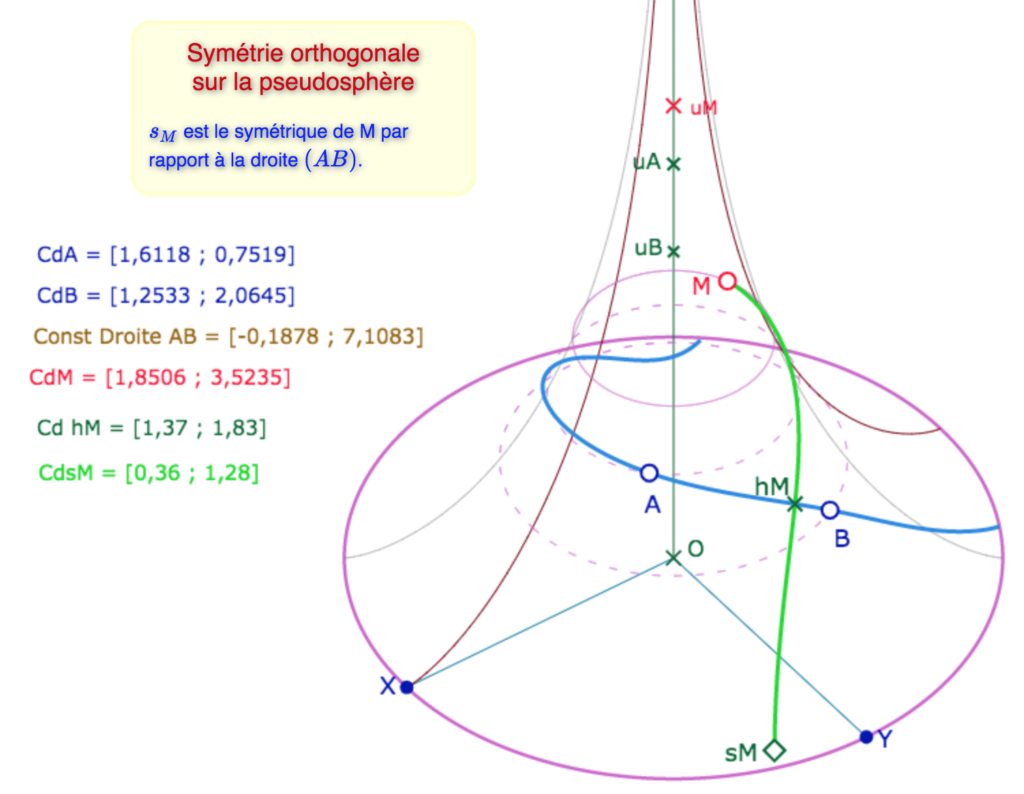
\(M\) parcourant le cercle de latitude \(u_M\), on voit que le symétrique peut sortir de la pseudosphère
L’équidistante
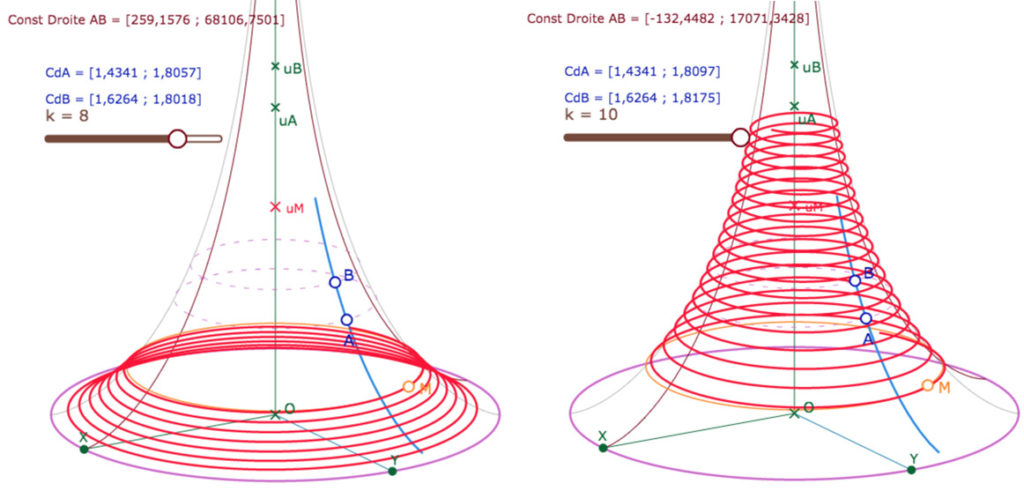
Dans la figure suivante, on a ajouté la droite \((MsymM)\) pour illustrer que l’équidistante n’est pas une droite.
On peut agir sur les points \(A, B, M\) et leurs latitudes, ainsi que sur le point \(tetaK\) qui permet de déplacer \(PtDrt\).
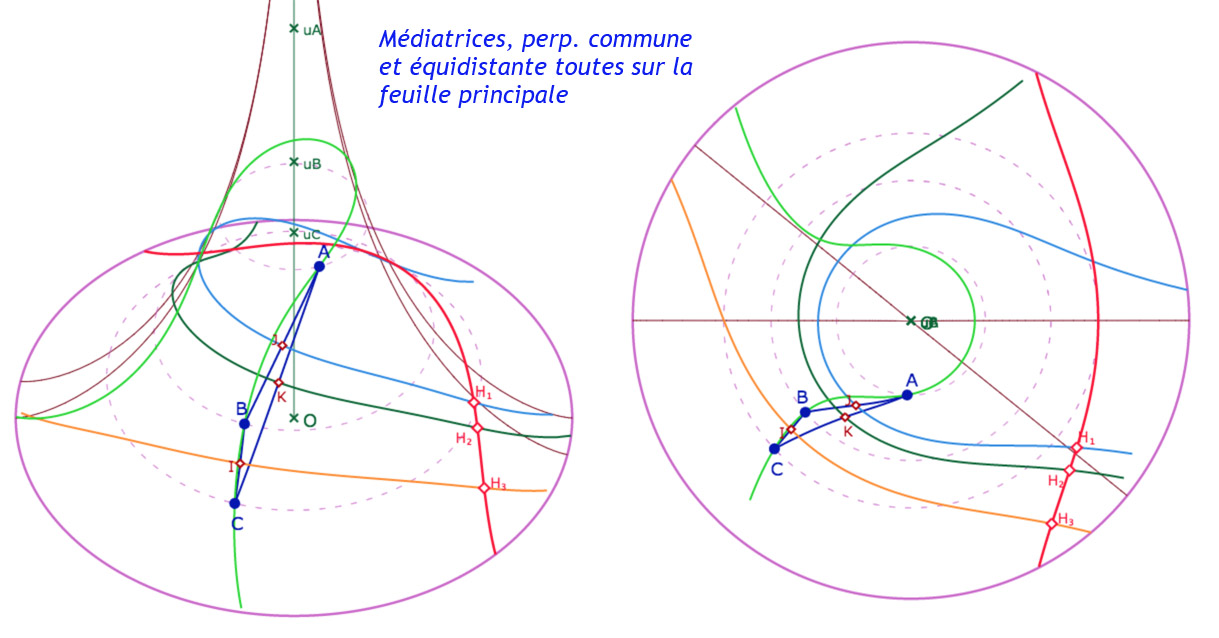
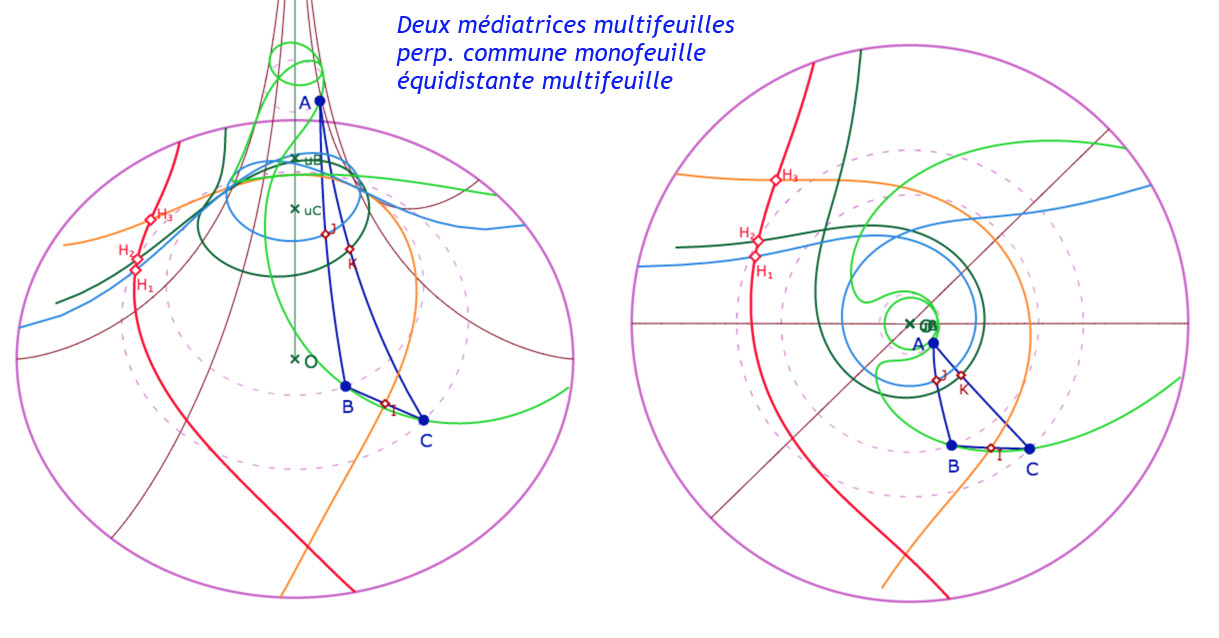
Figure que l’on applique bien entendu aux médiatrices d’un triangle. La perpendiculaire commune est la droite rouge, l’équidistante, la courbe verte.
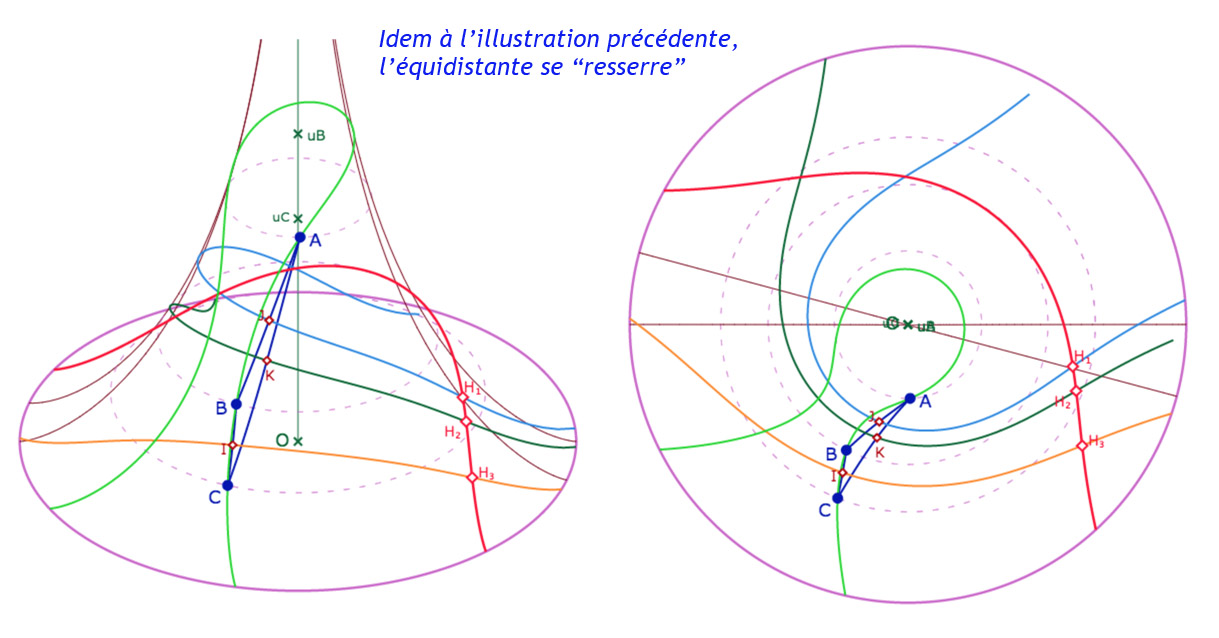
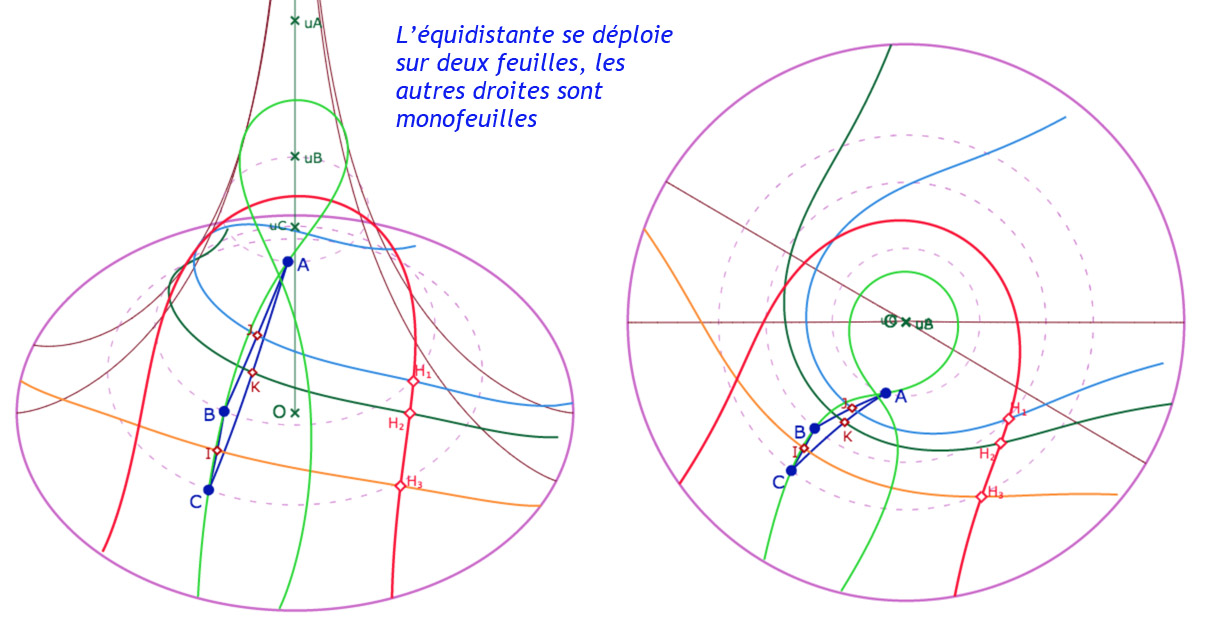
Galerie de 4 configurations de l’équidistante à la perpendiculaire commune des médiatrices d’un triangle
passant par un des sommets … Elle passe bien par les autres sommets ...
Manipulation de la figure
Modifier – légèrement – les points, les latitudes. Tourner la pseudosphère
Quand on compare au modèle du disque de Poincaré, on peut être surpris de l’enroulement multi-feuille de l’équidistante . On y reviendra quand on abordera la relation au « disque limite » de Beltrami : ce sera plus clair.
Les horicycles
On a déjà dit que la pseudosphère n’est pas un modèle de tout le plan hyperbolique, et en particulier elle ne donne accès qu’à un seul point à l’infini, et donc qu’à une série d’horicycles concentriques, de centre, ce point idéal. Reste que tout horicycle du plan hyperbolique est l’image d’un horicycle de centre un point donné par une symétrie orthogonale bien choisie. Et donc par symétrie, depuis un seul point idéal, on peut atteindre tous les horicycles.
Les seuls horicycles simples de la pseudosphère sont les cercles parallèles à l’équateur, ceux sur lesquels on place les points dans les figures. Les horicycles associés du plan hyperbolique sont alors représentés par l’enroulement infini, dans les deux sens, sur ces cercles. Tous ces horicycles ont même centre, l’unique point à l’infini de la pseudosphère. Ils sont donc concentriques. Ce point à l’infini est aussi le point de convergence, à l’infini des méridiens de la pseudosphère. On comprend que Beltrami ait pu avoir quelques difficultés pour défendre ses idées, très novatrices à l’époque, sur ce premier modèle – qui plus est local – du plan hyperbolique sur une surface.
Pour nos constructions, le fait de disposer de ces horicycles particuliers sur la pseudosphère est suffisant. Cela permet de construire la trace, sur la pseudosphère, des autres horicycles, simplement par le symétrique orthogonal de ces cercles par rapport à une des droites hyperboliques. Bien entendu, comme on a vu que le symétrique d’un point peut ne pas être sur la surface, il faut être prudent dans les choix effectués pour les illustrations
On peut donc illustrer, largement, la forme de la trace des horicycles sur la pseudosphère. « Trace » car, un point mobile sur un cercle parallèle à l’équateur, un horicycle \(h_{equ}\), n’ayant une longitude d’amplitude limitée à \(2\pi\), on n’a qu’une partie de l’horicycle. Pour situer voici une illustration simple :
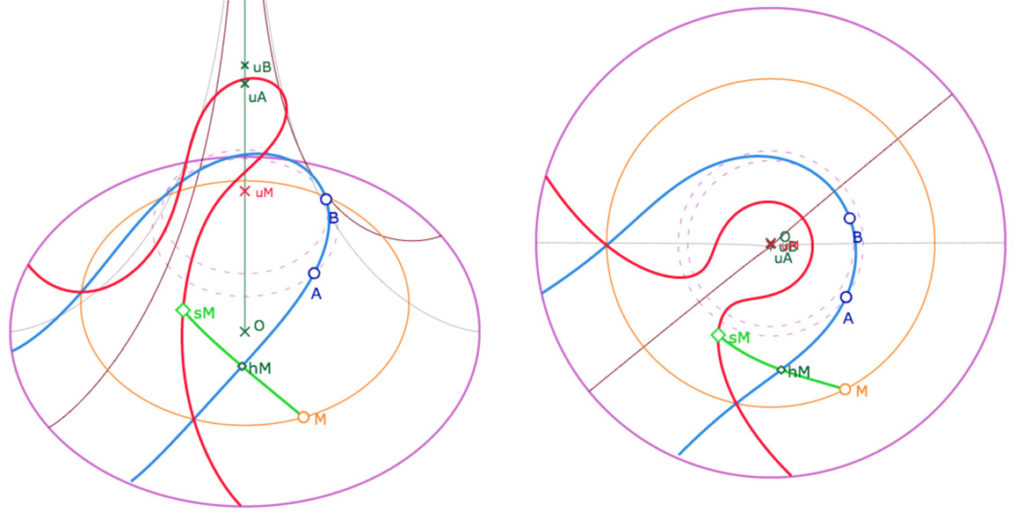
Un point \(M\) est sur un cercle parallèle à l’équateur.
Le lieu du symétrique de \(M\) par rapport à \((AB)\) est la trace de l’horicycle, en rouge sur la figure.
Par ailleurs, un horicycle \(H\) étant donné, il est l’image d’un des horicycles concentriques \(h_{equ}\) provenant des cercles parallèles à l’équateur de la pseudosphère par une symétrie orthogonale bien choisie. Alors pour cette symétrie, tout triangle inscrit dans cet horicycle \(H\) est l’image d’un triangle de l’horicycle \(h_{equ}\). Ainsi, même si l’infini n’est pas directement accessible sur la pseudosphère, il est facile de construire des triangles, sur la pseudosphère, dont le cycle circonscrit est l’horicycle que l’on vient de construire. Bien entendu on ne va atteindre de cette façon tous les triangles de l’horicycle, au moins à cause de l’enroulement sur la pseudosphère qu’on ne reproduit pas pour les points initiaux. Avant de manipuler la figure correspondante, voici quelques précisions et illustrations :
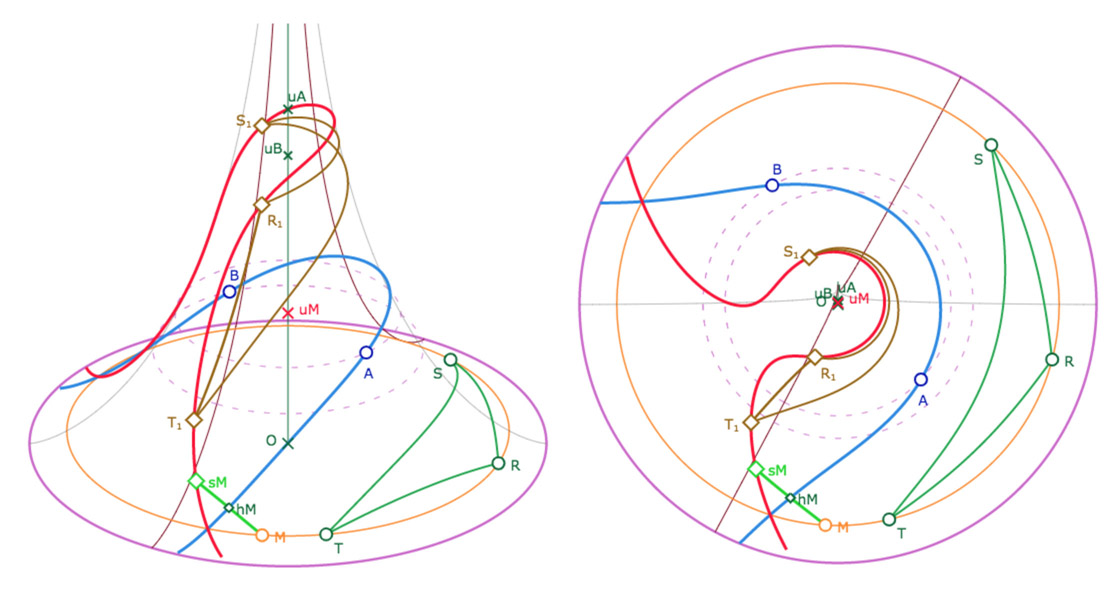
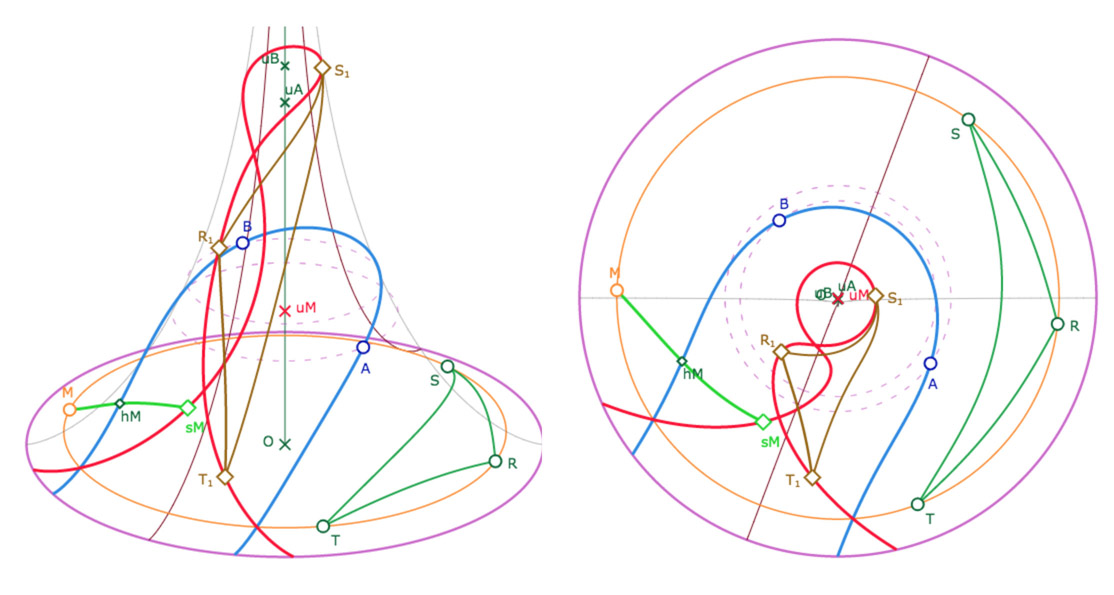
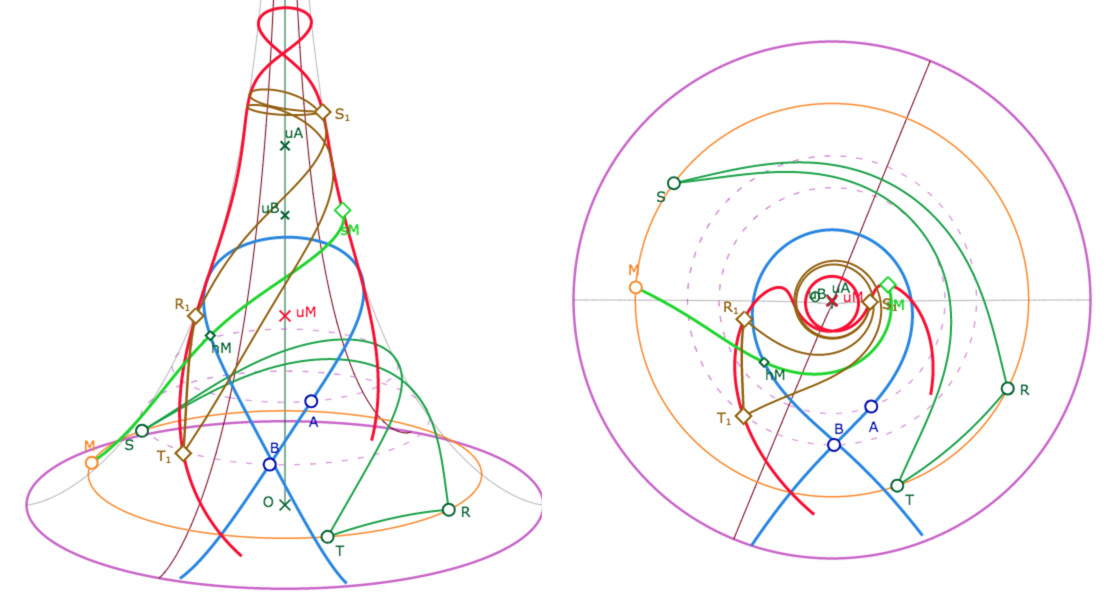
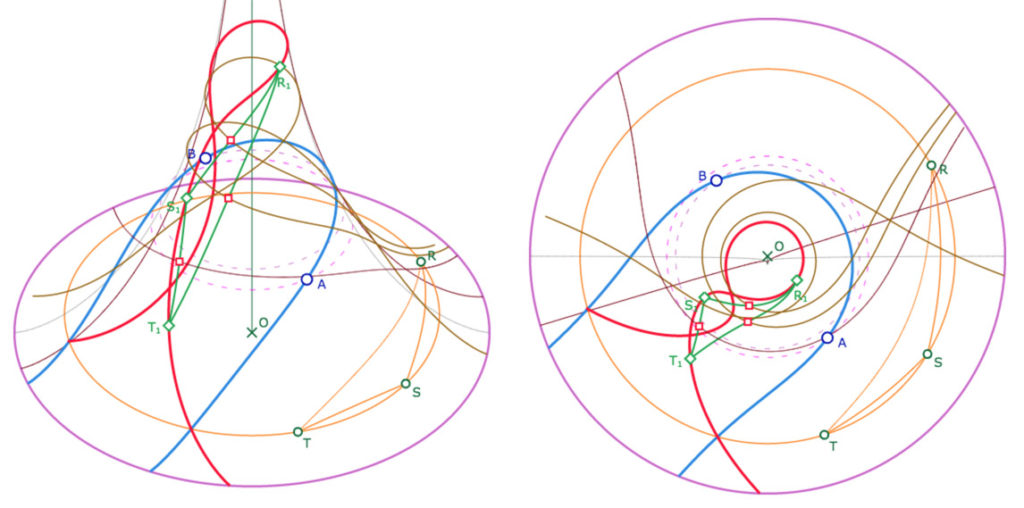
Dans les illustrations et la figure suivantes, On a une droite \((AB)\) en bleu, un point \(M\) sur un horicycle d’altitude \(u_M\) (orange). On a tracé, en rouge, l’image de (la partie) de l’horicycle – le cercle orange – dans la symétrie orthogonale de droite \((AB)\). En vert, un triangle \(RST\) dont les sommet sont sur l’horicycle initial. En marron le triangle image \(R_1S_1T_1\).
Galerie de trois illustrations : un horicycle monofeuille, un horicycle sur deux feuilles, un horicycle plus complexe, sur plusieurs feuilles.
La figure de manipulation
La figure est assez riche, vous pouvez agir sur les latitudes des points \(A\), \(B\), \(M\),
les points eux-même (et \(M\) pour parcourir l’horicycle).
Construire des parallèles sur la pseudosphère
Comme le lecteur a pu le constater, il est visuellement impossible de distinguer, sur la pseudosphère, la trace d’une équidistante ou celle d’un horicycle. De même, quand trois droites sont en pinceau, comme les hauteurs ou les médiatrices d’un triangle, on ne peut pas distinguer sur la pseudosphère, toujours visuellement, quand elles ne sont pas concourantes sur la pseudosphère, si elles sont concourantes en dehors de la pseudosphère, ou si elles ont une perpendiculaire commune (hors pseudosphère) voire sont parallèles.
Pour illustrer une situation donnée il faut donc savoir, en pratique, que l’on est dans la situation que l’on souhaite illustrer. Or la figure précédente est l’occasion de construire des droites dont on sait qu’elles sont parallèles : il suffit de construire les médiatrices d’un triangle inscrit dans un horicycle, comme le triangle \(R_1S_1T_1\).
On notera que cela ne sert pas de construire les médiatrices de \(RST\) car ce sont des méridiens qui sont en pinceaux sans support, convergent vers l’unique point idéal disponible sur la pseudosphère.
Voici donc deux illustrations de droites parallèles
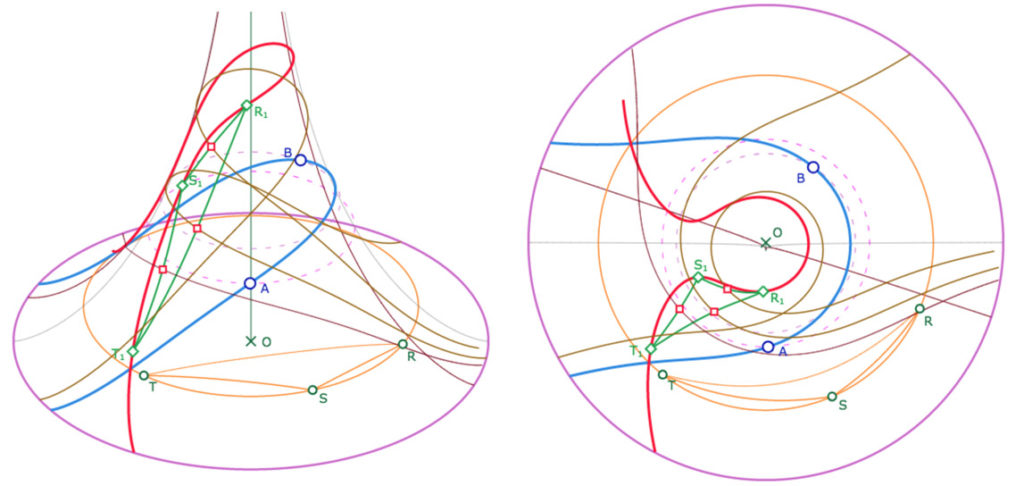
(couleurs modifiées pour plus de lisibilité)
Nous n’avons pas ajouté cette figure dans cette page, déjà un peu lourde. On peut la voir en ligne ici. Les manipulations sont les mêmes que dans les figures précédentes.
Compléments
Pour réaliser des figures intrinsèques sur la pseudosphère, consulter cet article.
En particulier, on reviendra sur les horicycles pour réaliser des horicycles « très enroulés » sur la surface comme cela :