Après la pseudosphère usuelle, qui permet d’atteindre un seul point à l’infini du plan hyperbolique – on peut alors dire qu’elle est « parabolique » – puis la version hyperbolique, qui, elle, permet d’atteindre deux point à l’infini, on aborde la troisième surface pseudosphérique de révolution, celle de type elliptique qui n’a aucun point à l’infini. Il en résulte que l’on va rencontrer une situation différente des deux autres surface, vis à vis de l’enroulement de la surface sur elle-même et de la bijection crée entre la surface et son image dans KB.
Approximation de la surface
On reprend la même démarche que pour la PSH. En pratique, là encore, le seul travail qui demande un peu d’attention est dans l’approximation de la nappe par une double interpolation de Lagrange. Même si on obtient un peu plus rapidement la même précision de l’approximation que dans le cas de la PSH, compte tenu de la forme de la nappe, on a conservé le même type de polynôme pour l’approximation : polynôme de degré 4 en le paramètre \(p\) et de degré 5 en fonction de \(u\).
La description de la nappe de la surface
Étant donné le paramètre \(p\), réel positif, la courbe de la surface elliptique dans le plan frontal – la génératrice – est régie par la relation :
\(\left\lbrace \begin{array}{1} x(u) = p \, sh(u)\\ z(u) = \displaystyle \int_0^u \sqrt{1-p^2ch^2(t)} \,dt\end{array} \right.\) avec \(-sh^{-1}\displaystyle \left( \frac{\sqrt{1-p^2}}{p} \right) \le u \le sh^{-1}\displaystyle \left( \frac{\sqrt{1-p^2}}{p} \right)\)
Le polygone obtenu pour la génératrice
g(u)=(-3.77301 p4+4.36908 p3-1.89728x p2+0.276375 p-0.015376) u5
+ (-0.515445 p4+0.622785 p3-0.457166 p2+0.120633 p+0.00842376) u3
+ (-0.658574 p4+0.722747 p3-0.897874 p2+0.13101 p+0.961048) u
ce que l’on écrira, comme pour la PSH, sous la forme \(g(u)= \left(Coef_{p5}u^4+Coef_{p3}u^2+Coef_{p1} \right)u\) où les coefficients ne dépendent que de \(p\) et ne sont recalculés – une seule fois pour toute la figure – que si on modifié le paramètre.
La surface a une forme de cône, en particulier elle est non régulière à l’origine. Comme pour la pseudosphère, pour ces questions de singularité, on s’intéresse à un seul demi-cône. Traditionnellement, on retient celui du bas.
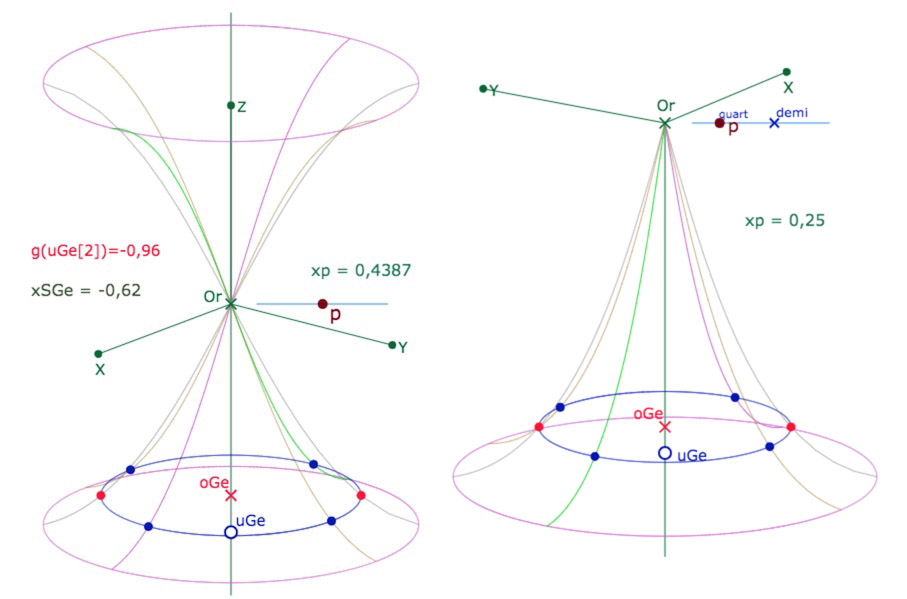
à gauche, la surface entière, à droite la partie retenue pour la représentation des figures sur la PSE.
On ne revient pas les constructions intermédiaires, ce sont les mêmes, aux adaptations près, que pour la PSH. On retrouve six méridiens, dont deux « fixes » (en gris clair, les lieux des deux points rouges) qui correspondent au sommet de l’ellipse représentant le cercle en 3D. La limite de la feuille principale a été fixée en longitude nulle pour la partie supérieure de la surface (méridien vert, sur l’axe des abscisse) qui devient finalement de longitude \(-\pi\) pour la partie inférieure. Donc la feuille principale de la PSE sera sur l’amplitude longitudinale de \(]-\pi,\, \pi]\).
Dans l’illustration de droite, on a laissé apparaître les points « quart » et « moitié ». Le point \(p\) est en effet très légèrement aimanté (2 pixels) par ces deux points pour que le paramètre prenne les valeurs exactes de 0,25 et 0,50 pour une raison que l’on voit tout de suite à la prochaine section.
Conjugaison avec KB – Premières droites
En dehors des méridiens, toujours d’équation \(\theta=Cst\), les autres géodésiques de la PSE sont déterminées (avec \(k\) et \(c\) deux constantes) par la relation : \(\theta =\displaystyle \frac{1}{p}tan^{-1}\left(\displaystyle \frac{c \, ch(u)}{\sqrt{p^2sh^2(u)-c^2}}\right)+k\).
Comme pour la PSH, une construction intrinsèque à partir de deux points \(A(u_A, \theta_A)\) et \(B(u_B, \theta_B)\) n’est pas possible, mais la correspondance entre la PSE et le « disque limite » de Beltrami (le modèle KB) est très simple à mettre en oeuvre… et c’est pour cela que l’on peut faire ces figures.
Ainsi, le passage de la PSE \((u, \theta)\) vers KB \((x, y)\) est donné par \(\left\lbrace \begin{array}{1} x= th(u) \, cos(p \theta)\\ y=th(u) \, sin(p \theta)\end{array} \right.\).
Ces informations proviennent toujours de : Modern Differential Geometry of curves and surfaces with Mathematica – Alfred Gray – 1997 (2° Ed.).
Chapitre 19 : Surfaces of constant gaussian curvature.
On peut déjà représenter la feuille principale de la PSE par cette projection centrée à l’origine du cercle limite de Beltrami. Comme \(|th \, u|<1 \) on voit que l’image de la PSE est bornée : aucun point à l’infini. L’image de la PSE est un cercle hyperbolique centré en l’origine, et donc un cercle euclidien, de rayon \(th(u_{max})\). Et comme le centre du cercle du modèle de Klein-Beltrami est un point (le seul) en lequel les angles sont conformes, les différentes feuilles de la PSE vont être de la même taille que la feuille principale dans le modèle KB, chacune recouvrant \(2p\pi\). Il en résulte une conséquence qui différencie significativement ce modèle pseudosphérique des des deux autres : contrairement à la PS ou la PSH, l’enroulement infini sur la PSE n’est plus bijectif dans KB : quelques feuilles suffisent à recouvrir la partie du plan hyperbolique image de la surface. Et même, rapidement, les feuilles de la PSE se chevauchent dans la projection sur KB.
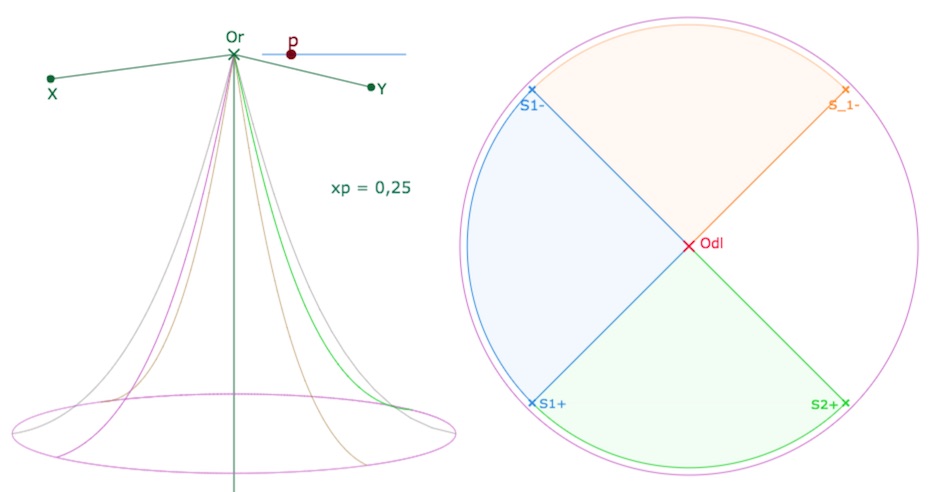
En bleu la feuille principale \((]-\pi,\, \pi])\), en vert la feuille suivante \((]\pi,\, 3\pi])\), £en orange, la feuille précédente \((]-3\pi,\, -\pi])\). Pour \(p=0,25\), l’image de la PSE est recouverte par 4 feuilles.
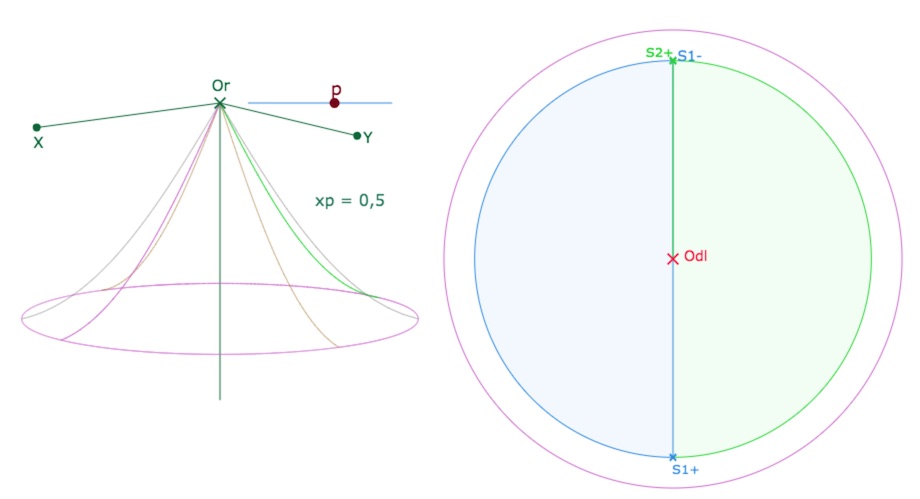
Pour p=0,50, le cercle image de la PSE est recouvert avec seulement deux feuilles.
Construction d’une droite sur la PSE
Tout d’abord on reprend les premières macros de placement d’un point sur la PSE elle-même : le cercle 3D parallèle à l’équateur de latitude \(u_A\) était un horicycle pour la PS, une équidistante pour la PSH, est un simple cercle – hyperbolique mais aussi euclidien – pour la PSE. Ensuite la construction d’un point projeté sur KB se traite en une seule ligne, comme dans le cas de la surface hyperbolique. Pour le retour sur la PSE, on reprend la même démarche que pour la PSH : depuis deux points \(A\) et \(B\) de la surface, et leurs images \(A_{kb}\) et \(B_{kb}\) dans KB, on prend un point \(M_{kb}\) de la droite \((A_{kb}B_{kb})\). On calcule ses coordonnées beltramiennes \((u, \theta)\) – c’est l’expression \(CdM\) – qui permet de placer le point \(M\). Et, comme avec la PSH, on en déduit deux macros, une qui renvoie simplement le point, car on peut avoir besoin d’un seul point – milieux, pieds des hauteurs, point de concours, etc – ou, si on veut la droite, on fait le lieu du point \(M\), et la macro qui va avec.
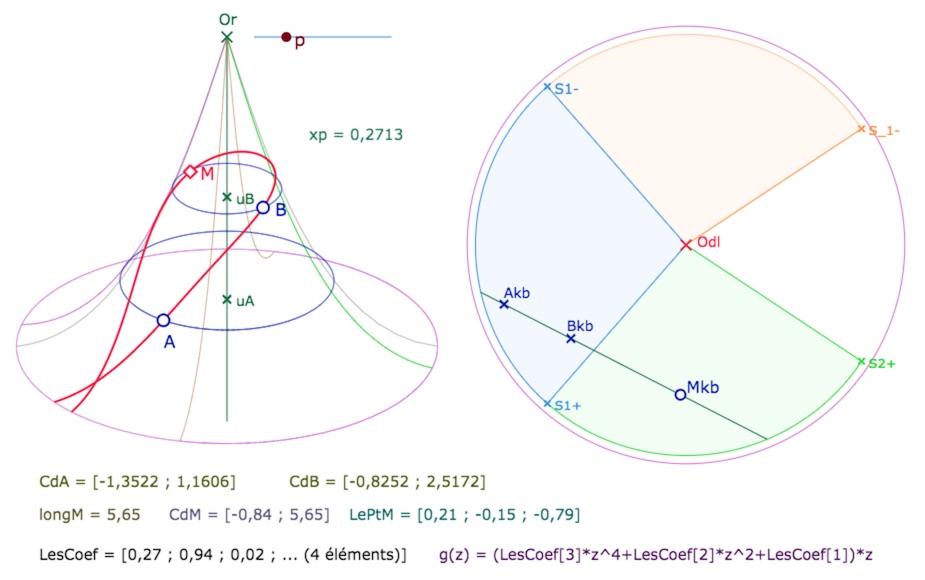
Construction d’une droite multifeuille sur la pseudosphère elliptique
Quelques détails sur la construction
• Pour avoir une droite multifeuille qui fonctionne pour tout \(p\), il suffit de construire l’intersection de la droite KB avec l’image de la PSE, soit le cercle (ici caché) de centre \(Odl\) passant par \(S_1^+\).
• Pour plus de lisibilité des figures, nous allons faire, au prochain paragraphe, une macro « droite de la feuille principale ».
• Les méridiens ne sont pas traités par la macro associée.
• Le seul point sur lequel il faut prendre quelques précautions est dans le calcul de la longitude de \(M\) (longM dans la figure) pour qu’elle puisse être multifeuille, justement. A priori, longM a pour expression \(\displaystyle \frac{1}{xp} \; tan^{-1} \left( \frac{y(Mkb)-y(Odl)}{x(Mkb)-x(Odl)} \right)\), mais \(tan^{-1}\) ne renvoie un angle que sur \(\displaystyle ]-\frac{\pi}{2}, \frac{\pi}{2}[\). En pratique, le résultat n’est correct que si \(x(M_{kb})<x(O_{dl})\). Pour avoir un résultat multifeuille, il faut ajouter ou retrancher \(\pi\) selon la position de la droite \((A_{kb}B_{kb})\) par rapport au centre du cercle. Cette modification « bi-booléenne » convient pour toutes les situations (éviter les méridiens bien entendu):
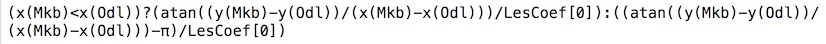
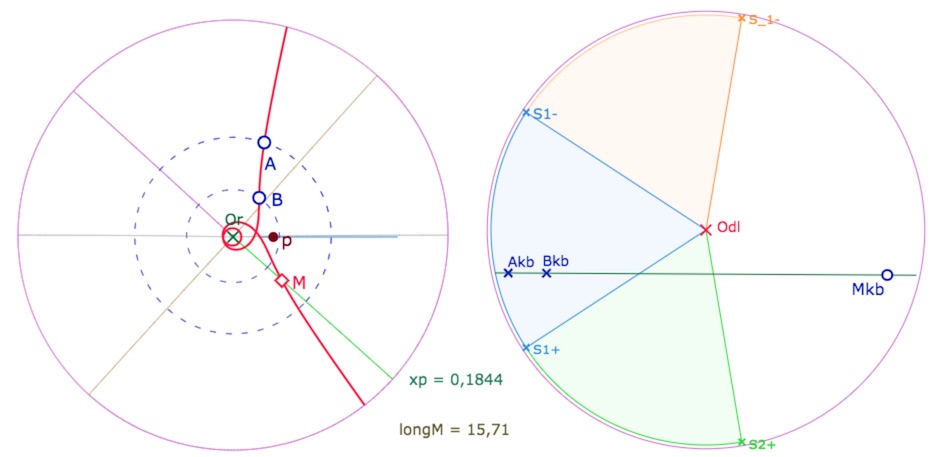
Exemple d’une vue de dessus, avec une droite sur 4 feuilles (longitude de \(M\) supérieure à 4π)
Manipulation de la figure associée
Agir sur \(p\), puis les points \(A\) ou \(B\) ou leurs latitudes \(u_A\) et \(u_B\).
Préférer ouvrir cette première figure PSE dans un nouvel onglet.
Rappel : dans la page DGPad, être en mode « consultation » (flèche de gauche inactive) pour tourner facilement la surface, et agir sur les points plus simplement.
Réalisation, dans KB, d’une droite « Feuille principale » pour la PSE
On se donne deux points \(A_{kb}\) et \(B_{kb}\) dans la feuille principale de KB. La droite passant par ces deux point peut couper
• l’arc de cercle en deux points \(Barc_1\) et \(Barc_2\), (B pour Bord)
• le segment délimitant la longitude \(-\pi\) en \(Binf\)
• le segment délimitant la longitude \(\pi\) en \(Bsup\)
Le segment à construire peut prendre six expressions. Pour rendre compte du code retenu, on a placé une version « Blockly » puis facilement lisible, mais la version blockly n’est pas utilisable – c’est juste « une démo » – en macro, d’où la vraie écriture en JavaScript.
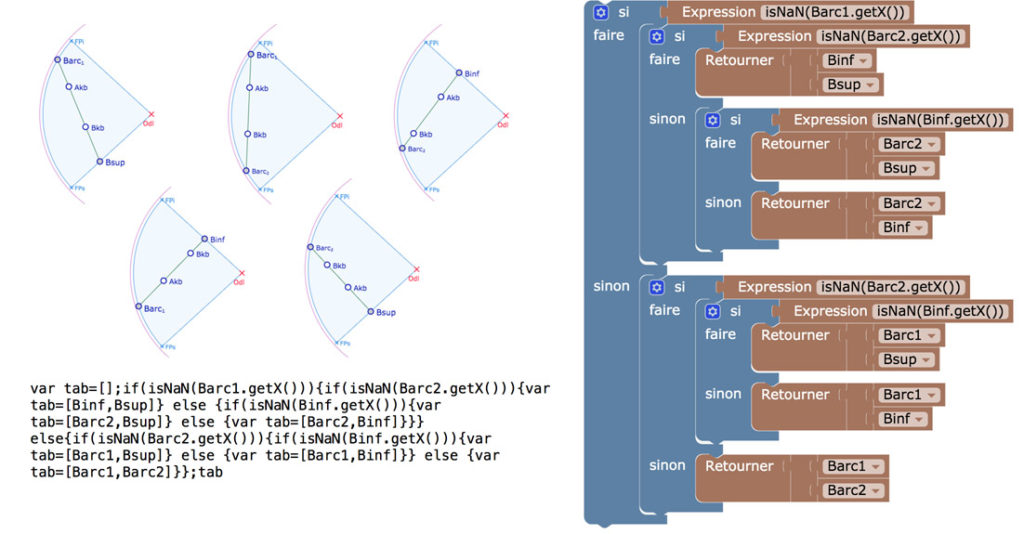
Manipuler la figure associée
Manipuler les points \(A_{kb}\) et \(B_{kb}\)
Préférer ouvrir la figure dans un nouvel onglet
Premières figures de base
Le remplissage d’un polygone se fait, simplement, comme déjà expliqué en détail pour la PSH.
Les médianes d’un triangle
Médianes d’un triangle sur la PSE avec triangle rempli. Déplacer les points sur la PSE ou leurs latitudes
Préférer ouvrir la figure dans un nouvel onglet
Les hauteurs
On met en pratique l’utilisation de la distinction entre droite dans la feuille principale et droite multifeuille (en particulier pour la perpendiculaire commune). Commençons par deux illustrations
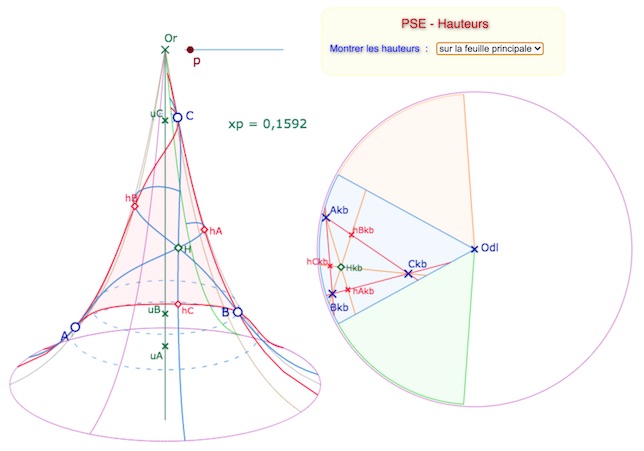
Ci-dessus, avec l’orthocentre et les hauteurs limitées à la feuille principale.
Ci-dessous, cas des hauteurs « en faisceau à axe » avec la perpendiculaire commune (rose),
entièrement sur une autre feuille (donc moins lisiblesur la PSE, sauf à la faire tourner).
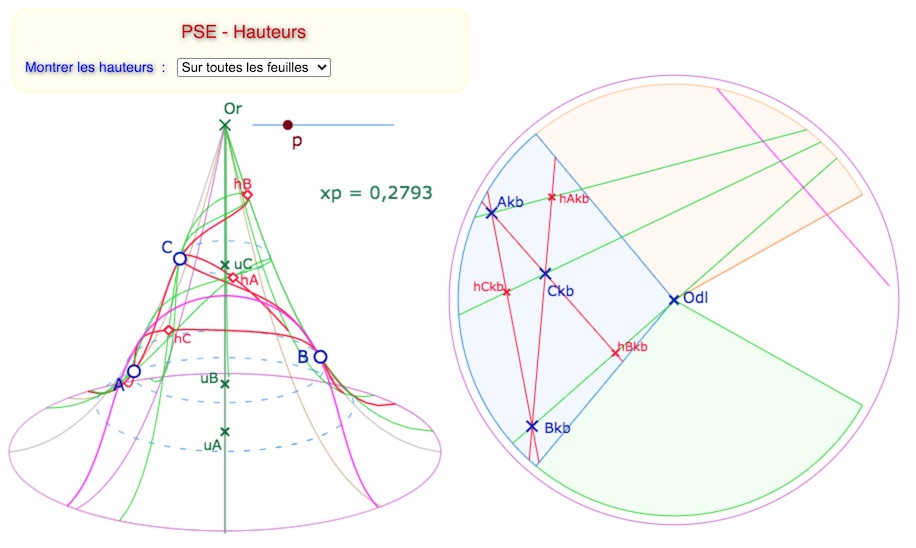
Manipuler la figure
Préférer ouvrir la figure dans un nouvel onglet. Dans cette figure, vous pouvez aussi remplir le triangle sur la PSE avec la macro « remplir TR » (non disponible ci-dessus, les macros n’étant pas accessibles) en montrant, \(LesCoef, g\), le point \(Odl\) puis les trois points \(Akb, Bkb\) et \(Ckb\).
Le cercle circonscrit
On peut faire une figure similaire. Le cercle circonscrit ne pose pas de problème particulier. On a choisi de cacher le cercle quand il commence à déborder de la surface.
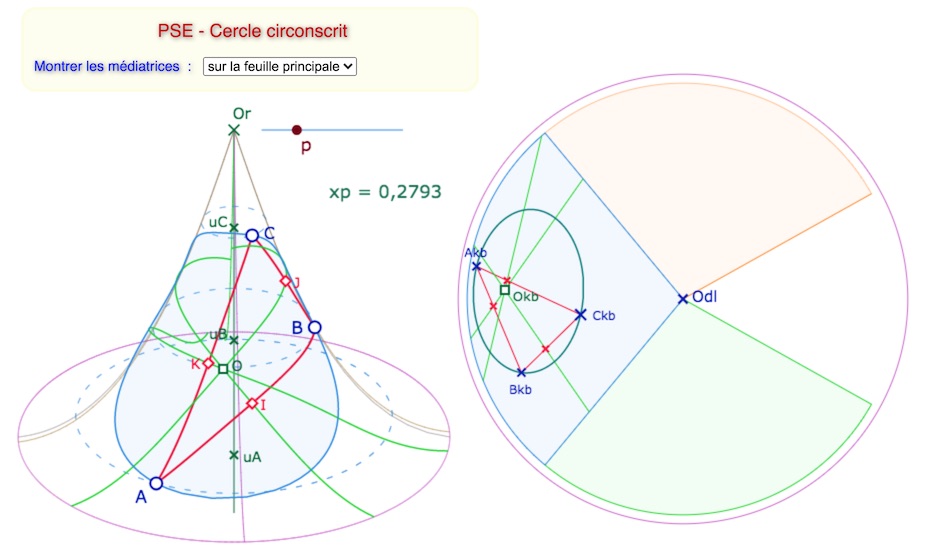
Ci-dessus :cercle circonscrit sur la PSE avec les médiatrices limitées à la feuille principale
ci-dessous, avec la perpendiculaire commune aux médiatrices
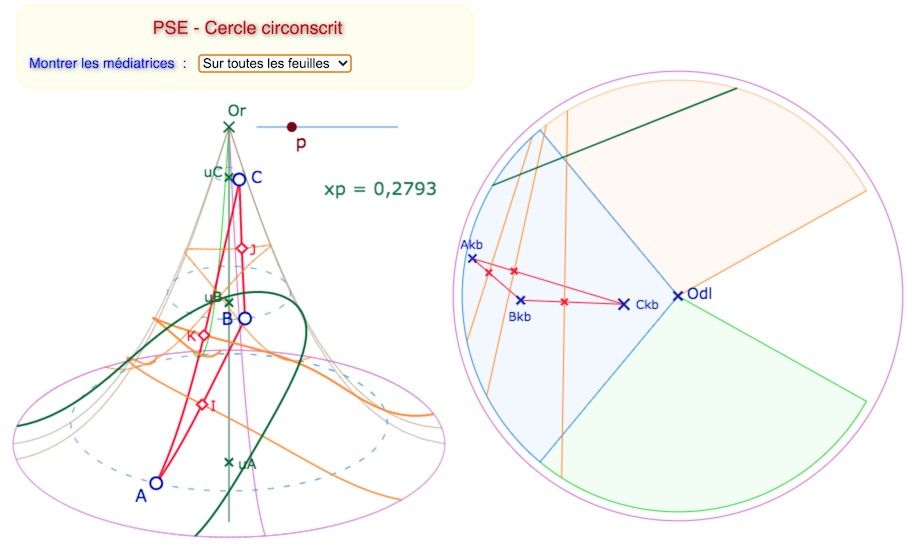
Manipulation de cette figure
Manipuler la figure pour passer d’une configuration de base à celle ci-dessus. Penser à modifier le paramètre p.
on a choisi , pour ces premières figures de ne pas construire l’équidistante pour que la figure soit rapidement téléchargeable.
En lançant cette version de la figure dans un nouvel onglet, on peut utiliser la macro « remplir TR ».
Dans la page suivante, on poursuit les figures sur cette surface, avec de belles constructions sur les trilatères..