Cette page se proposant d’aller plus loin, on a choisi de faire réellement découvrir les propriétés évoquées aux lecteurs en leur faisant finaliser les figures par eux-mêmes. Cela signifie que vous allez être amené à utiliser des macros-constructions. Une page d’explication a été rédigée à cet effet, avec deux exemples simples que l’on peut reprendre.
La géométrie des pinceaux
On a vu que les droites remarquables d’un triangle, en général, sont en pinceau (vérifié sur les hauteurs et les médiatrices). Autrement dit, on a constaté, d’un point de vue heuristique, qu’elles ont quelque chose en commun : un point (pinceau à centre), une perpendiculaire commune (pinceau à axe) ou un point à l’infini (les droites parallèles, pinceau sans support).
De ce point de vue, la géométrie euclidienne est une géométrie dans laquelle il n’y a que deux types de droites en faisceau, car les pinceaux à axe et sans support sont confondus.
On peut ensuite définir une notion de pinceau de droites de la façon suivante : Deux droites \(a\) et \(a\) définissent le faisceau \([latex]\mathscr{P}_{ab}\)[/latex] qui est l’ensemble des droites \(c\) telles que les trois droites \(a, b, c\) sont en pinceau.
On rappelle que, du point de vue de la théorie sous-jacente, trois droites sont en pinceau si la composée des trois symétries orthogonales associées est encore une symétrie orthogonale.
Depuis la rédaction de cette page, un menu Bachmann a été ajouté au site. Ce sont, entre autres, les théorèmes de transitivité de l’axiomatique de Bachmann.
Cette notion de pinceau de droite permet de définir un nouvel objet mathématique : le trilatère.
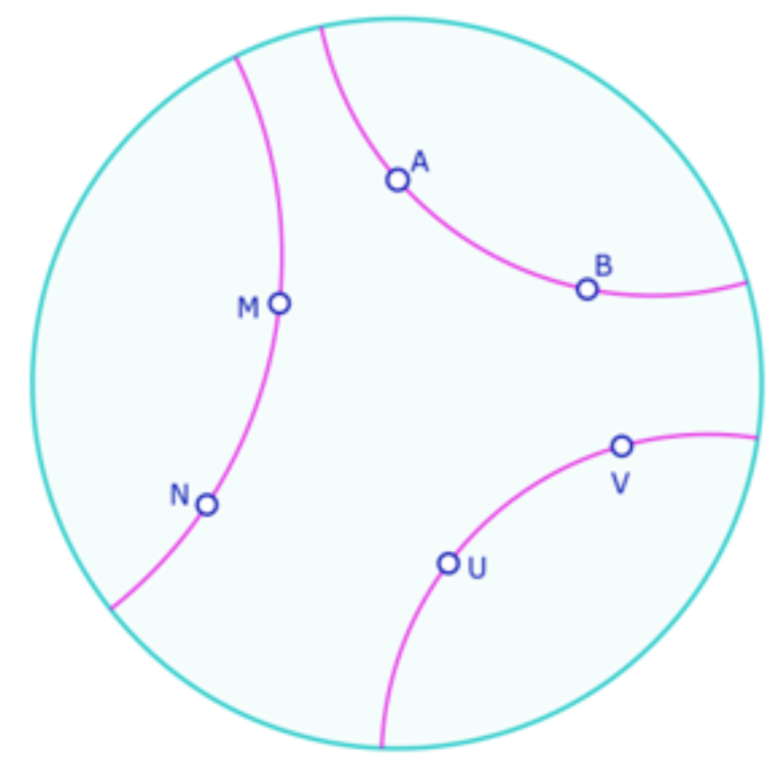
Un trilatère est un ensemble de trois droites qui ne sont pas en pinceau. Il peut être sans sommet, comme ci-contre, ou avec un, deux, ou trois sommets (triangle).
Le trilatère est donc une extension hyperbolique naturelle, mais aussi très générale, des triangles.
On se propose ici d’explorer quelques propriétés de la géométrie des trilatères. Mais on commence par les propriétés des pinceaux.
Propriété de base : par un point il passe une et une seule droite appartenant à un pinceau de droites donné.
La preuve est une application immédiate du théorème de Hjelmselv.
En terme de géométrie dynamique, l’intérêt est de construire réellement cette droite en tant de « droite du pinceau », c’est-à-dire indépendamment de la nature du pinceau. C’est facile à réaliser car on fait la construction au sein d’un modèle euclidien donc avec les outils de ce modèle.
Dans la figure suivante, (on a laissé l’ancien vocabulaire « faisceau » à la place de « pinceau ») nous vous proposons de construire cette droite et de vérifier qu’elle est bien une droite du pinceau.
Etape 1. Sélectionner l’icone des macros. Commencer par construire la droite du pinceau des deux droites passant par M.
( montrer dans l’ordre, le cercle horizon, droite 1, droite 2, point)
Etape 2. Déplacer les points pour rendre les deux droites sécantes et vérifier que la droite construite passe bien par le point d’intersection.
Etape 3. Rendre à nouveau les droites non sécantes, construire leur perpendiculaire commune, puis vérifier à nouveau que, dans ce cas, la droite construite est bien aussi dans le pinceau des droites (AB) et (PQ) par exemple en construisant la perpendiculaire commune à la nouvelle droite et une des deux droites du pinceau. On peut ou non colorier l’un des deux pour voir qu’elles sont superposées et donc que les trois droites sont bien en pinceau.
Exemple d’application
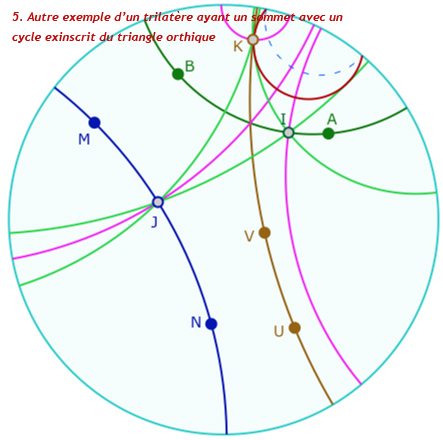
On a vu (ici) que les cycles exinscrits d’un triangle peuvent être des équidistantes. En particulier le second point de Ajima Malfatti – point de concours, dans le cas euclidien, des trois droites passant par le centre d’un cercle exinscrit et le point de contact des deux cercles de Malfatti tangents au côté associé – ne peut pas se construire de la même façon que le cas euclidien. La propriété s’étend pourtant au cas hyperbolique, et la construction se fait alors avec la notion de pinceau, et la macro précédente. C’est ce qui est proposé d’illustrer dans la figure suivante.
Manipulation proposée :
a) afficher les points de contact et les bissectrices extérieures
b) utiliser la macro «Droite du faisceau par un point» pour construire la version hyperbolique de ce point. (horizon, droite, droite, point)
Intersection de deux pincceaux

Dans la figure suivante, on dispose d’un ensemble de macros, sous forme de 4 dossiers, dont celui sur les faisceaux, avec 3 macros, dont celle sur l’intersection de deux pinceaux (faisceaux).
A priori deux pinceaux n’ont pas toujours une droite d’intersection, et s’ils en ont une, elle est unique. La macro attends 5 objets, le cercle horizon, puis deux cercles (droites hyperboliques) pour le premier pinceau et deux autres pour le second pinceau. Dans la figure à l’ouverture, la droite rouge est l’intersection du pinceau vert avec le pinceau mauve. Commencer par le vérifier, au moins sur le cas où les pinceaux deviennent à centre.
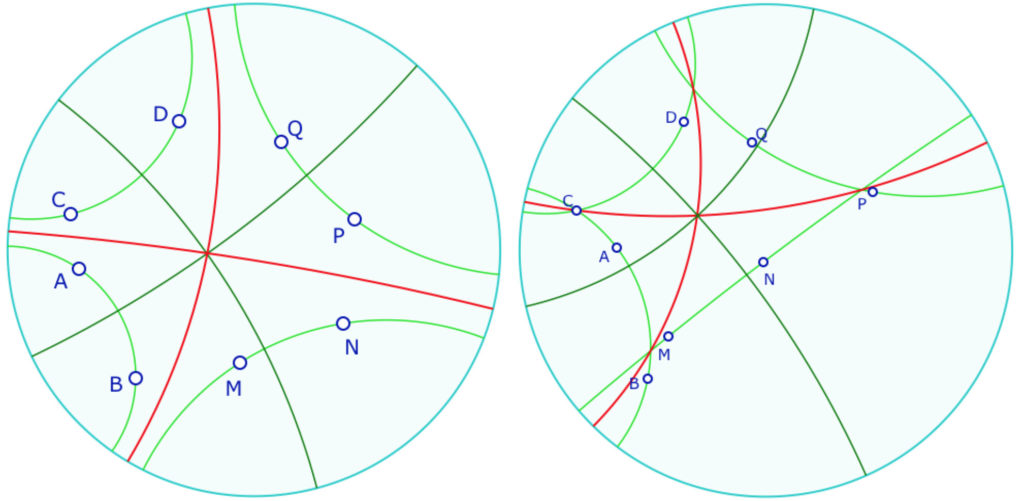
Construire ensuite la seconde intersection possible entre deux autres pinceaux. La troisième possibilité de pinceaux, , comme \((CD),(MN)\) et \((AB),(PQ)\) ne peut pas avoir d’intersection.
On peut ensuite ajouter, en vert ci-contre, les perpendiculaires communes, justement, aux deux pinceaux mentionnés ci-dessus.
Essayer de faire coïncider les deux intersections des droites rouges et vertes.
Quelle serait figure euclidienne si les pinceaux sont tous à centre et les intersections confondues ?
Hauteurs d’un trilatère et application
Dans la figure suivante on dispose d’un trilatère, et de la hauteur (rose) du trilatère, issue de deux droites (les deux marrons) orthogonale à la troisième (bleue).
La macro utilisée (nommée ci-dessus Hauteur de faisceau ffd) attend 4 cercles, soit, dans l’ordre, l’horizon, les deux droites qui définissent le pinceau (ff) et la troisième droite (d) dont on veut la perpendiculaire appartenant au faisceau ff.
Manipulations proposées :
1. Construire ainsi les deux autres hauteurs du trilatère. Dans cette configuration, les hauteurs existent toutes les trois, et sont sécantes. On constate qu’elles sont en faisceau à centre
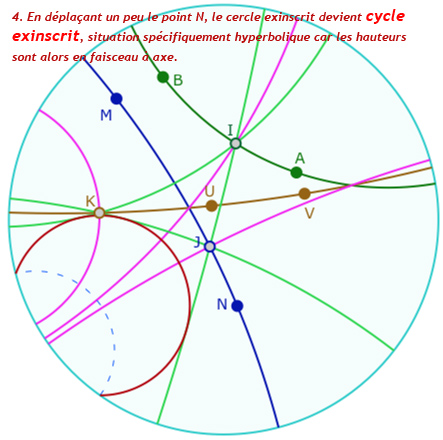
2. Déplacer les points de base pour que les hauteurs ne soient pas concourantes. Une hauteur peut ne pas exister, mais quand elles existent toutes les trois, l’axiomatique de Bachmann montre qu’elles sont en pinceau (et donc ici en pinceau à axe). Vous pouvez éventuellement le vérifier en prenant les perpendiculaires communes des hauteurs, deux à deux.
Le triangle orthique d’un trilatère
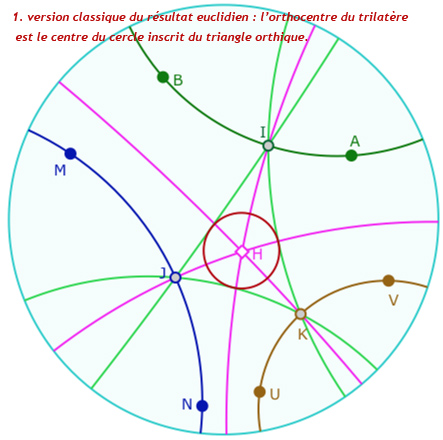
Quand une hauteur existe, le pied de la hauteur existe aussi. Donc si les trois hauteurs d’un trilatère existent, le triangle orthique, c’est-à-dire le triangle du pied des hauteurs aussi. Dans le cadre euclidien, c’est un exercice classique que de voir que l’orthocentre d’un triangle – dans certaines conditions d’angles, il faut qu’il soit à l’intérieur du triangle – est le centre du cercle inscrit du triangle orthique.
Cela signifie aussi que les hauteurs du triangle \(ABC\) sont les bissectrices du triangle des pieds des hauteurs \(IJK\).
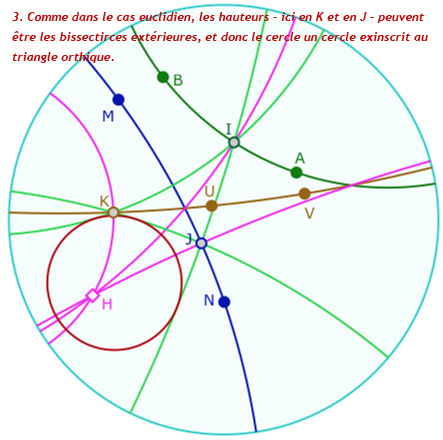
Sans les conditions d’angles, quand l’orthocentre est extérieur au triangle, il est alors le centre d’un cercle exinscrit au triangle orthique.
Cette propriété qui se démontre souvent avec des outils typiquement euclidiens (produit scalaire, aire) est en fait une propriété absolue, vraie aussi sur les trilatères, qui se démontre facilement.
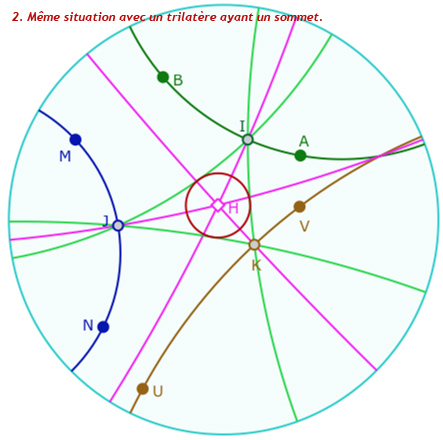
Mais bien entendu la propriété est, encore une fois, bien plus riche avec les trilatères.
La galerie ci-dessus présente cinq illustration d’explorations
que l’on peut réaliser avec la figure suivante.
D’un point de vue théorique, ces configurations a priori si différentes sont des instances de la même situation : il n’y a qu’une preuve bien entendu.
Préférer ouvrir cette figure dans un nouvel onglet