Il s’agit, dans cette page, d’illustrer très modestement juste quelques points du mémoire de Beltrami, qui plus est, de manière non technique. D’autres aspects, et en particulier des aspects plus numériques comme les angles, seront abordés, avec le temps, dans les articles de Blog.
Beltrami est resté célèbre pour sa première réalisation concrète, réelle, bien que seulement locale, du plan hyperbolique sur une surface plongée dans l’espace euclidien. Mais ce n’est pas sans difficulté qu’il a dû défendre, non seulement sa profonde compréhension de la géométrie différentielle, mais aussi des idées nouvelles, encore novatrices pour certaines, et parfois difficilement exprimables avec clarté à une époque où l’on s’interrogeait pour savoir si des équations définissaient intrinsèquement une surface, ou s’il y avait du sens à justifier l’existence d’une géométrie non euclidienne par la consistance des calculs analytiques qui la fondaient…
Même si la géométrie des surfaces à courbure constante négative est naturellement celle des plans de Lobatchevsky, il reste que ce modèle, dans son détail, est réputé assez obscur, en partie à cause d’une complexité intrinsèque due à l’enroulement des feuilles sur la surface, même si la situation était très claire pour Beltrami :
« La longueur de la zone est indéfinie, et par suite la zone s’enroule un nombre fini de fois sur la surface de révolution ; à cette occasion, il faut observer que les points qui se superposent de cette manière les uns aux autres doivent être toujours considérés comme distincts, sans quoi le théorème, que par deux points de la surface passe une seule ligne géodésique, cesserait d’être vrai. »
Saggio di interpretazione della geometrica non euclidea … » – Beltrami – 1868
Le traducteur français des travaux de Beltrami – Jules Hoüel – prenait parfois lui-même la défense de ses idées et répondait à ses détracteurs les plus farouches. Ainsi, après trois années de polémiques, il devait encore écrire à Genocchi :
« La coïncidence fortuite de deux points d’une surface, ne changeant rien aux propriétés des figures, pourvu qu’on fasse toujours, comme dans les surfaces de Riemann, la distinction des nappes de la surface auxquelles elles appartiennent, me semble une preuve de la nécessité d’employer les coordonnées qui se rapportent non pas aux points de l’espace fixe dans lequel flotte la surface mais aux points flottants eux-mêmes »
Lettre de Hoüel à Genocchi du 16 juillet 1871
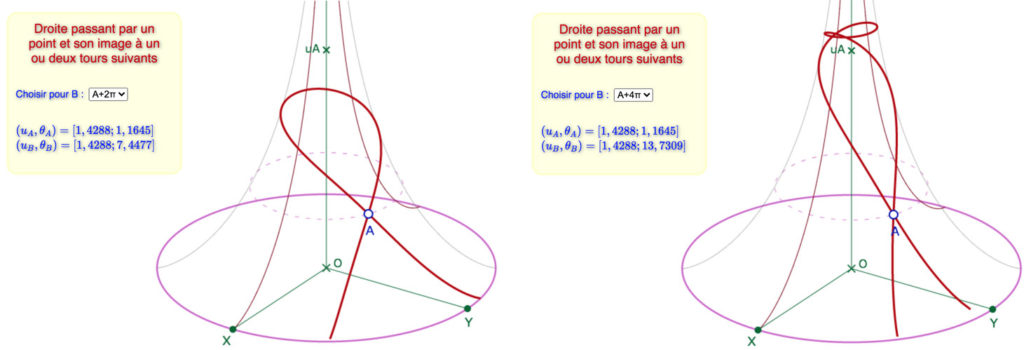
Illustration de l’enroulement de la pseudosphère sur elle-même :
à gauche la droite passant par un point et le point placé un tour plus loin, à droite la droite avec deux tours plus loin.
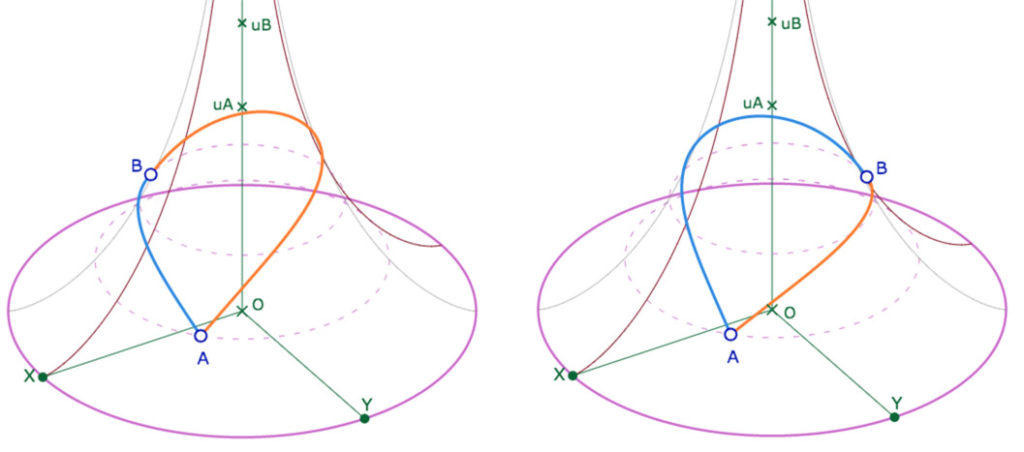
Deux segments \([AB]\) selon la position des points et la représentation de la feuille principale de la pseudosphère.
Les points réels et idéaux chez Beltrami et les points effectifs sur la pseudosphère
Une des difficultés du mémoire de Beltrami, en particulier pour ses contemporains, vient du fait qu’il parle généralement de « points réels » sur une surface pseudosphérique alors qu’il ne s’agit pas nécessairement de points qui appartiennent à la pseudosphère mais seulement des points de son disque-limite, le modèle KB présenté dans les pages précédentes. Nous avons alors choisi d’appeler dans cette page, points effectifs les points [du plan hyperbolique] qui seront effectivement sur la pseudosphère. Par exemple reprenant une illustration d’une page précédente sur les médiatrices d’un triangle, on voit bien une certaine confusion possible à vouloir appeler « réels » les points d’intersection entre la perpendiculaire commune et les médiatrices : ils sont réels dans KB mais n’existent pas sur la pseudosphère. Par contre les sommets du triangle sont des points effectifs de la pseudosphère.
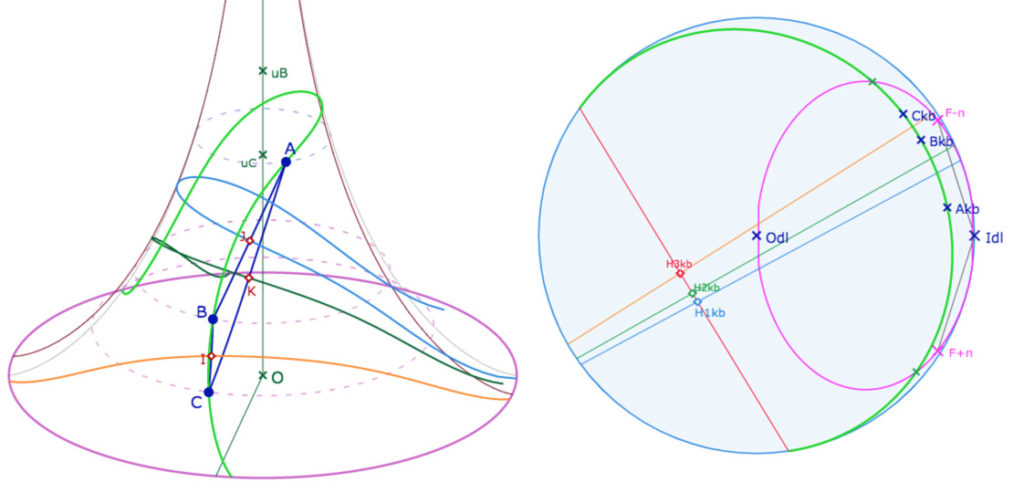
Les points \(H1_{kb}, H2_{kb}, H3_{kb}\) sont bien réels dans le plan hyperbolique KB mais ne correspondent
pas à des points effectifs de la pseudosphère.
Chez Beltrami, le terme réels utilisé pour les points du plan hyperbolique est utilisé en opposition à ce qu’il appelle les points idéaux qui sont les points du plan hors de son cercle-limite. En fait, depuis Klein, on peut dire que ce sont les points du plongement projectif naturel du plan hyperbolique.
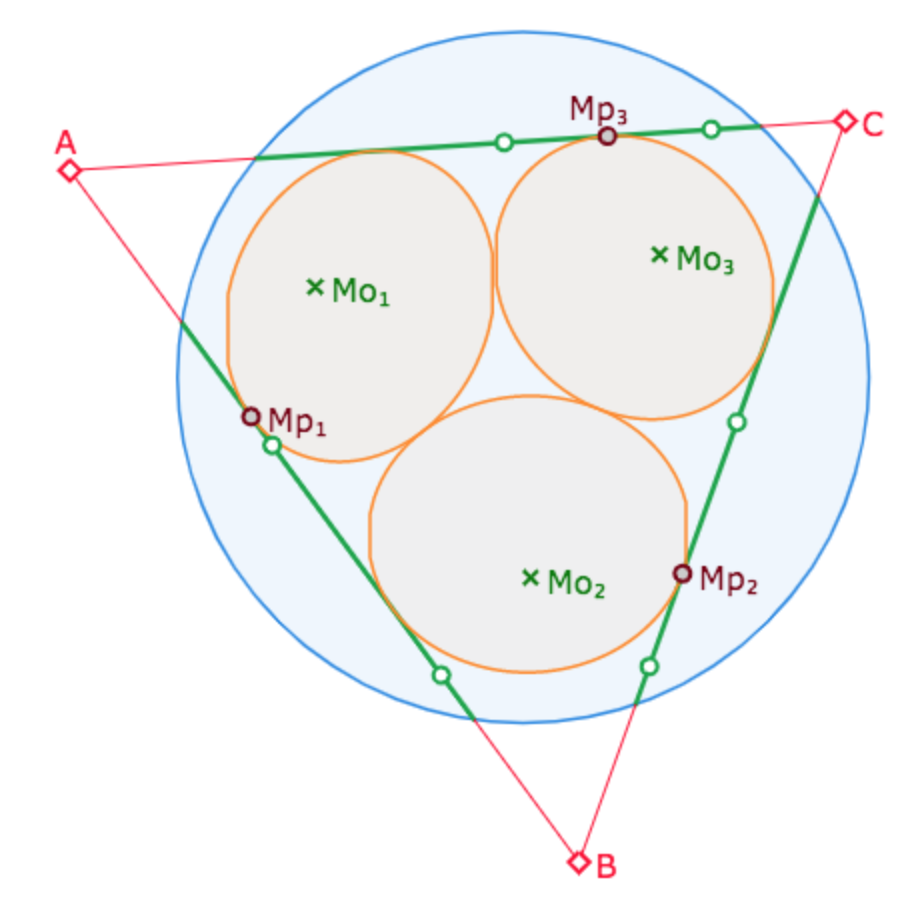
Ainsi – illustration ci-contre – ce qui pour nous est une figure « des cercles de Malfatti d’un trilatère dans le modèle KB » aurait été pour Beltrami une figure des cercles de Malfatti pour le triangle idéal ABC, même si, rappelons le, Beltrami n’avait pas vu que son disque limite était un modèle plan de la géométrie de Lobatchevsky.
Ci-contre, les KB-droites vertes sont pilotées par deux poignées. Les cercles de Malfatti sont de centre \(M_{o_{i}}\) passant par les points \(M_{p_{i}}\). Ce sont les cercles de Malfatti de ABC.
Dans le « Saggio » les points idéaux sont donc tout simplement les points en dehors du disque-limite, ce qui renforce le vocabulaire de points réels à l’intérieur du cercle vu la présence régulière de l’expression \(\sqrt{a^2-u^2-v^2}\) dans les calculs de Beltrami autour de ses coordonnées curvilignes.
Les coordonnées beltramiennes
Reprenons le déroulé du « Saggio ». Beltrami poursuit donc son travail initié en 1865, avec ses coordonnées curvilignes, et calcule l’angle entre deux lignes géodésiques u=constante et v=constante. Il rencontre alors le terme \(\sqrt{a^2-u^2-v^2}\) où \(a\) est une constante. Ses calculs n’ont ainsi de sens que pour \((u,v)\) – considérées maintenant comme coordonnées cartésiennes dans un plan euclidien – à l’intérieur d’un cercle de rayon \(a\) qu’il appelle cercle limite, et dont il montre en détail que les points correspondent aux points à l’infini de la surface qu’il étudie. Il en déduit :
« Donc les lignes géodésiques formant le système \(u = constante\) sont toutes orthogonales à la ligne géodésique \(v=0\) et les lignes géodésiques \(v= constante\) sont orthogonales aux lignes géodésiques \(u=0\). Cela revient à dire qu’au point \(u=0\) et \(v=0\) concourent deux lignes géodésiques orthogonales entre elles que nous appellerons fondamentales. …»
« Saggio di interpretazione … »
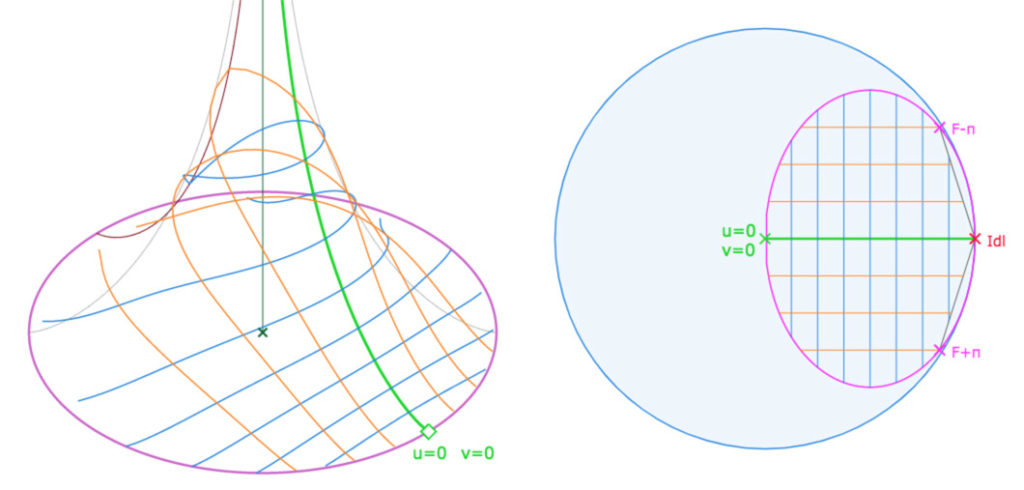
Les « géodésiques fondamentales » ne sont pas orthogonales entre elles, mais les géodésiques bleues sont toutes
orthogonales à la géodésique verte, ce qui se voit bien ci-dessous (car la pseudosphère est conforme)
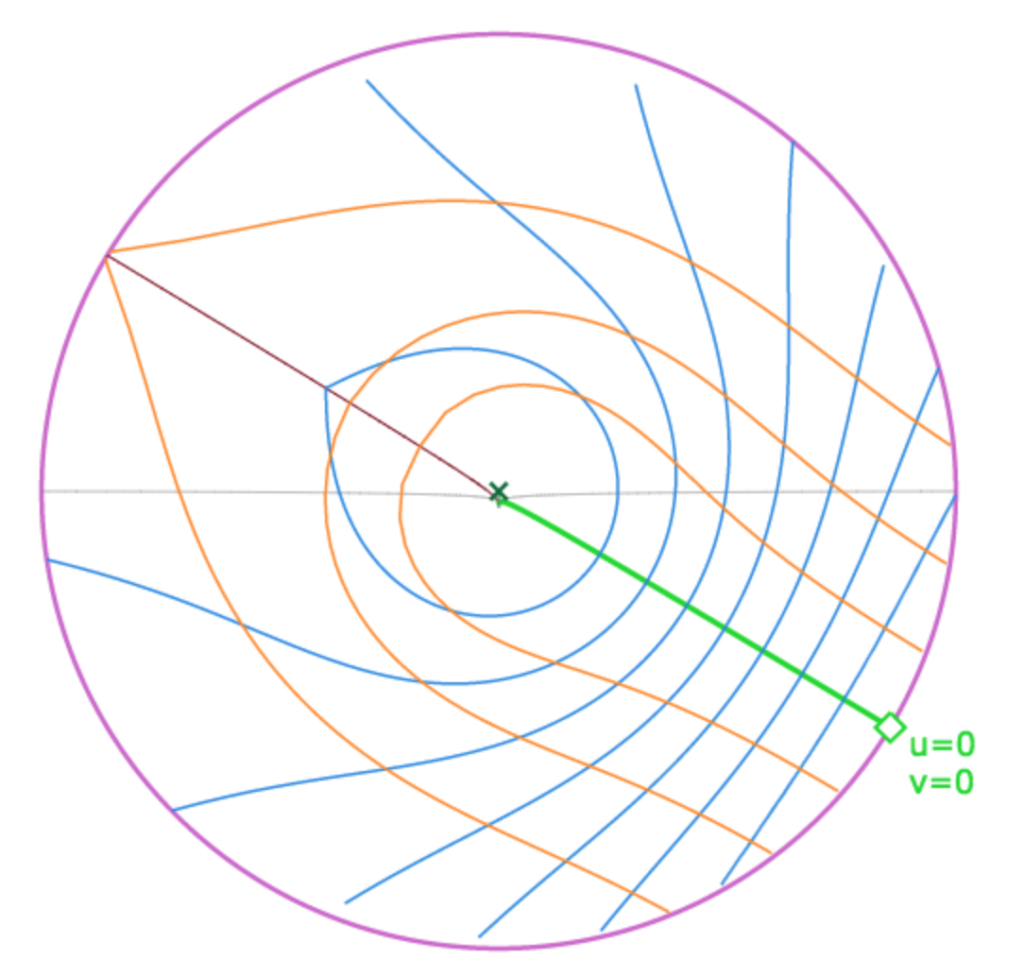
Un peu plus loin il écrit
«…et chaque point de la surface est déterminé comme intersection de deux lignes géodésiques menées par ce point perpendiculairement aux lignes fondamentales ce qui constitue évidemment une généralisation de la méthode cartésienne ordinaire. »
« Saggio … «
Et dans une note en fin d’article, il donne cette précision que nous allons illustrer
« … les lignes orthogonales à celles qui partent de l’origine sont représentées par les cordes du cercle-limite perpendiculaires aux diamètres qui représentent ces dernières lignes géodésiques. Réciproquement pour que deux lignes géodésiques se coupant en (u,v) soient représentées sur le plan auxiliaire par deux droites orthogonales, il faut que l’une ou l’autre de ces géodésiques passent par l’origine (u=0, v=0) »
« Saggio … » – Note de bas de page de la note 2 p. 284
Dans la figure suivante, on prend un point \(M_{kb}\) sur l’ellipse limite de la pseudosphère dans KB. Il est représenté par le point \(M\) sur l’équateur de la pseudosphère. On appelle \(N_{kb}\) le point dans KB (point limite de la PS) de la droite perpendiculaire en l’origine \(O_{dl}\) au segment \([O_{dl}M_{kb}]\). On le représente par \(N\) sur la pseudosphère c’est encore un point de l’équateur. On a noté ici \(O_b\) l’origine sur la pseudosphère des coordonnées beltramienne, image du point \(O_{dl}\).
On se propose d’illustrer la partie réciproque de la note. Pour cela on se donne un point \(U_{kb}\) du segment \([O_{dl}M_{kb}]\) et la perpendiculaire euclidienne au segment passant par le point. Sur cette perpendiculaire on se donne un point \(W_{kb}\) d’où on mène la perpendiculaire cette fois à \([O_{dl}N_{kb}]\), segment coupé en \(V_{kb}\). Ce que dit la note de Beltrami est que sur la pseudosphère, les droites correspondantes sont elles aussi perpendiculaires en les points « de retour » \(U\) et \(V\).
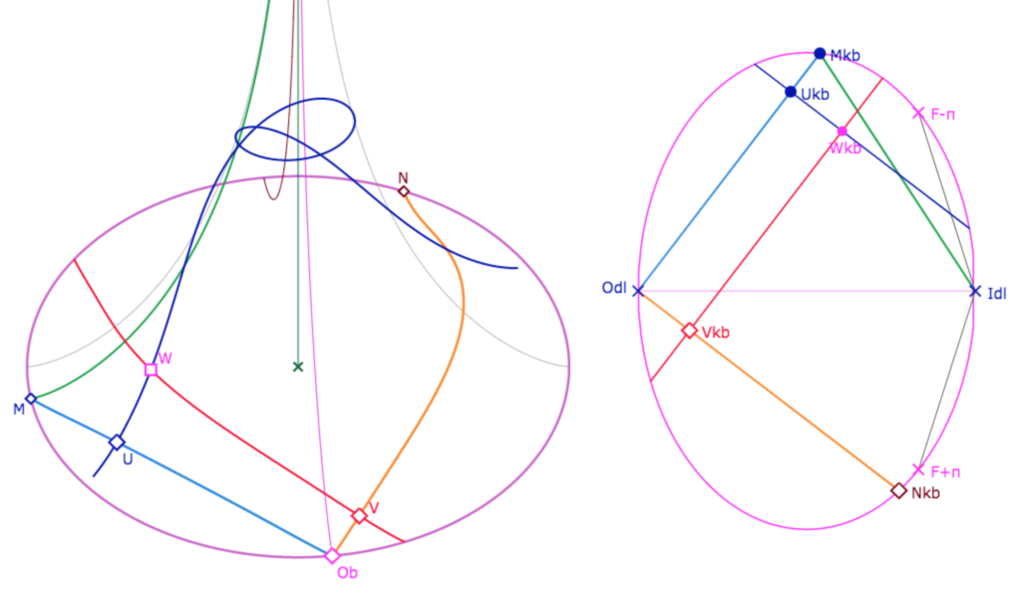
On constate, visuellement seulement, que le quadrilatère \(O_bVWU\) a trois angles droits, l’angle en \(W\) ne pouvant pas être droit puisqu’en géométrie hyperbolique la somme des angles d’un quadrilatère ne peut pas être égal à \(4\pi\). Dans KB le quadrilatère est un rectangle mais le modèle KB n’est pas conforme. Ce que dit la note est que les angles droits euclidiens en les trois autres points que \(W_{kb}\) sont aussi droits pour la géométrie de Lobatchevsky.

C’est remarquable comme résultat pour l’époque et montre bien la vision claire que Beltrami avait de son modèle. Cela dit, avec la vision projective du modèle KB, cela devient évident : en effet la KB-perpendiculaire à une droite en un point passe par le point et le pôle de la droite. Or le pôle d’un diamètre est à l’infini et donc la KB-perpendiculaire à un diamètre du « cercle-limite »est « trivialement’ la perpendiculaire euclidienne. C’est la raison pour laquelle nous n’avons pas détaillé plus avant les vérifications sur la pseudosphère (par des hauteurs par exemple). Il reste que cela produit de jolies illustrations. Par exemple on peut s’amuser à voir des cas particulier
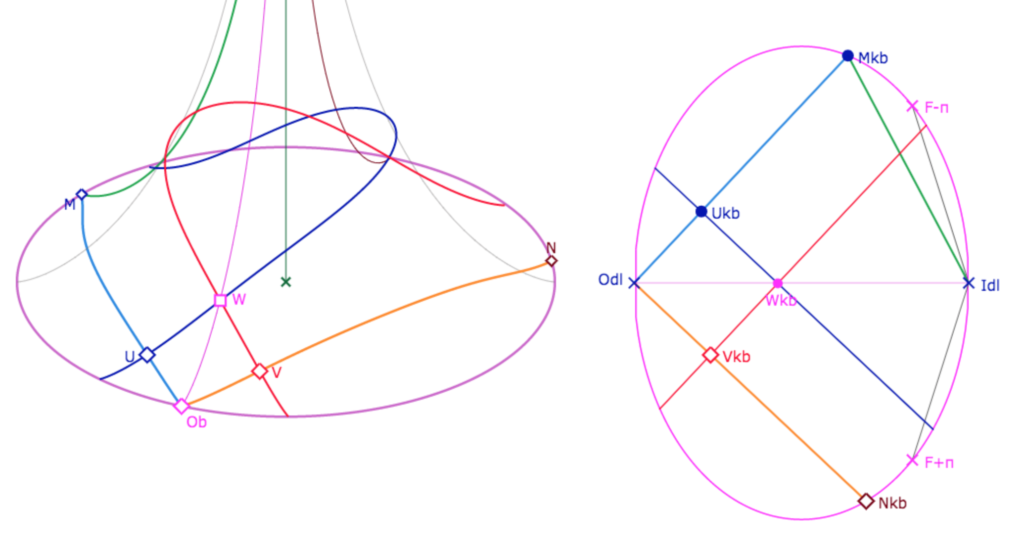

Manipulation de la figure associée
Dans cette figure, on peut agir sur les trois points de KB : \(M_{kb}\), \(U_{kb}\). et \(W_{kb}\).
On peut, comme dans les illustrations précédente, s’arranger à ce que les deux droites de départ restent dans la feuille principale.
On peut aussi régler les positions des deux points \(U_{kb}\) et \(W_{kb}\) pour que les droites restent dans la feuille principale ou la dépasse à peine.
Sur les horicycles
On passe directement à la quatrième partie du Saggio, la troisième partie, consacrée à l’émergence de la géométrie hyperbolique ayant déjà été abordée dans les pages précédentes. Dans cette partie, Beltrami se propose de « maintenant établir d’une manière plus concrète l’accord de la Géométrie pseudosphérique avec la Planimétrie non euclidienne ». Il commence par calculer ses propres formules d’angle de parallélisme et vérifie qu’aux notations près ce sont bien les mêmes que celles de Lobatchevsky. Il poursuit ensuite en retrouvant les formules d’aires de triangle ou de polygones avec sa propre démarche et retrouve le même défaut d’angle que Lobatchevsky.
Avant d’aborder directement les horicycles, nous allons nous attarder un peu sur ce passage du mémoire qui traite des « circonférences géodésiques », terme volontairement générique qui va regrouper chez Beltrami trois objets mathématiques différents au cours du développement de son argumentation. Bien entendu, il commence par les définir, de manière générale par un centre et un rayon. Puis après différents résultats intermédiaires, il s’intéresse aux médiatrices d’un triangle, plus précisément aux « lignes géodésiques élevées normalement sur les milieux des lignes de jonctions » pour remarquer qu’elles peuvent ne pas concourir en un point réel de la surface :
«[…], il faut nécessairement admettre que l’on ne peut pas toujours faire passer une circonférence géodésique par trois points de la surface choisis d’une manière quelconque. Cela encore est en accord, mutatis mutandis, avec les principes de Lobatchevsky »
« Essai d’interprétation … » p. 272
Beltrami poursuit en faisant son changement de cadre habituel : les cordes du cercle limite correspondant aux médiatrices du triangle image de son triangle géodésique peuvent se couper (en les prolongeant) en dehors du cercle limite, alors :
« […], il est permis de regarder les lignes géodésiques correspondantes comme ayant un point idéal commun, et leurs trajectoires orthogonales comme quelque chose d’analogue aux circonférences géodésiques proprement dites ».
Idem
Ce point de vue va être renforcé pour lui quand, calculant l’équation analytique de cette courbe géodésique de centre idéal, il trouve la même forme générale que pour le cercle mais avec une interprétation adaptée: en mettant en évidence une corde du cercle-limite bien particulière, la polaire du centre idéal extérieur au cercle – pour les médiatrices d’un triangle, c’est bien entendu leur perpendiculaire commune – la distance (le rayon du cercle) prend une autre signification et devient la distance à la géodésique correspondante. La constance de cette distance fait de la « circonférence géodésique » une équidistante :
« Cette équation définit une ligne géodésique réelle de la surface ; on peut donc en conclure que, parmi les circonférences géodésiques en nombre infini qui ont le même centre idéal, il y a toujours une ligne géodésique réelle et une seule de sorte que les circonférences géodésiques à centre idéal peuvent aussi se définir comme des courbes parallèles (géodésiquement) aux lignes géodésiques réelles ».
« Essai d’interprétation … » p. 274
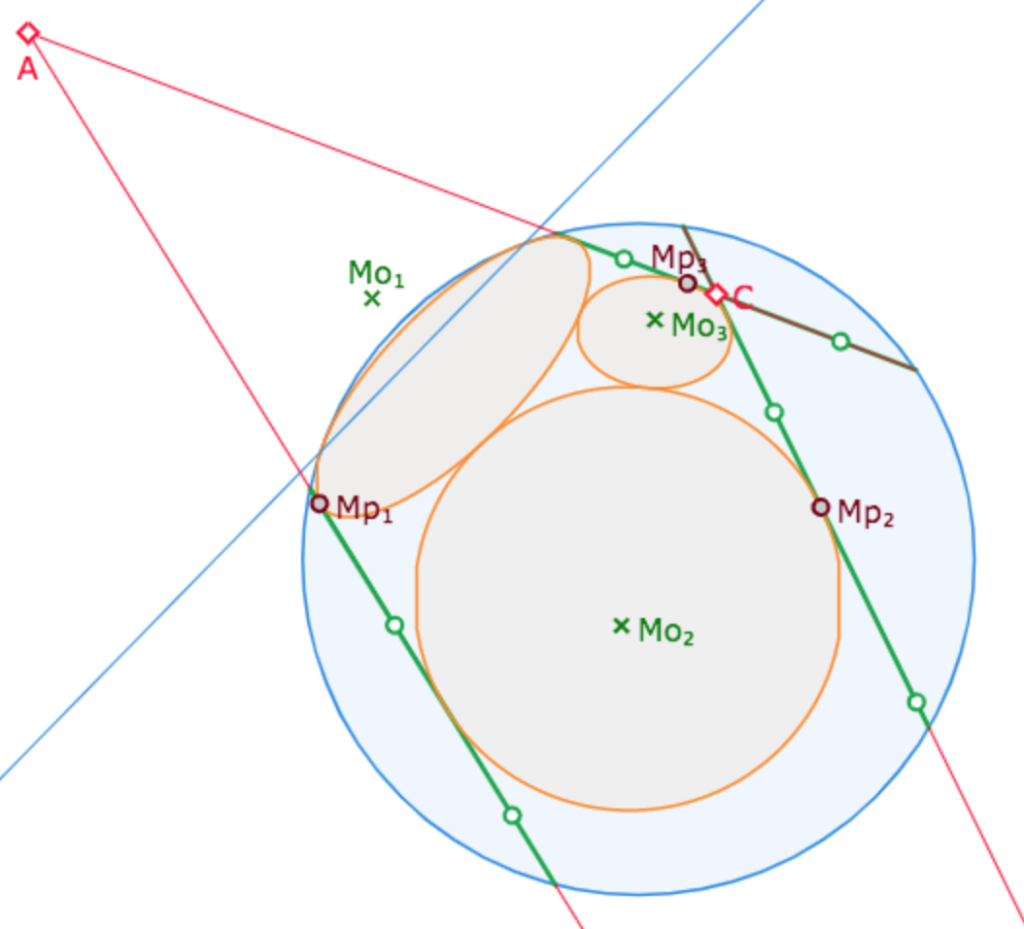
Illustration hors mémoire de Beltrami
Cette question de centre idéal extérieur au disque-limite peut surprendre en première lecture. Donnons en une illustration concrète, à nouveau sur notre figure des cercles de Malfatti d’un trilatère, vue plus haut.
Selon la configuration des droites originales (les droites vertes), le centre du cercle \(M_{o_{1}}\) peut sortir du disque-limite, et devenir un point idéal. Le KB-cercle est toujours représenté par une ellipse euclidienne. Dans ce cas l’ellipse est désormais bi-tangente au cercle-limite, et la polaire de son centre \(M_{o_{1}}\) est l’axe de l’équidistante, qui est aussi la droite passant par les deux points de contact entre l’ellipse et le cercle-limite.
Dans l’illustration suivante, on a un second centre de KB-cercle qui sort du disque-limite. Bien entendu – propriété des polaires – l’intersection \(K\) des deux polaires a lui-même pour polaire la droite des centres des deux cercles.
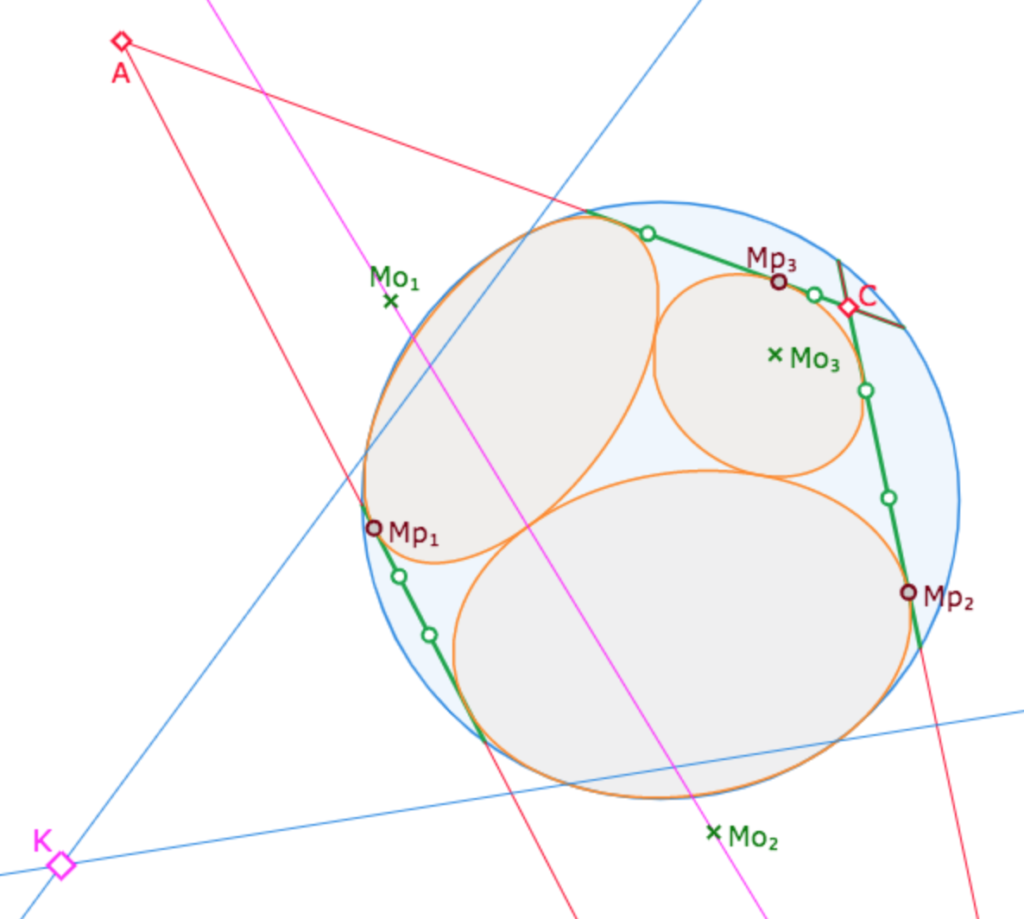
On peut manipuler cette figure en ligne (elle s’ouvre dans un nouvel onglet). La figure contient de nombreuses KB-macros. Bien entendu, on peut obtenir une configuration telle que le centre d’un des cercles soit – perceptivement – sur le cercle-limite, et donc représentant un horicycle pour KB. Thème que l’on aborde désormais.
Cette figure est aussi renvoyée sur la pseudosphère dans ce post de blog.
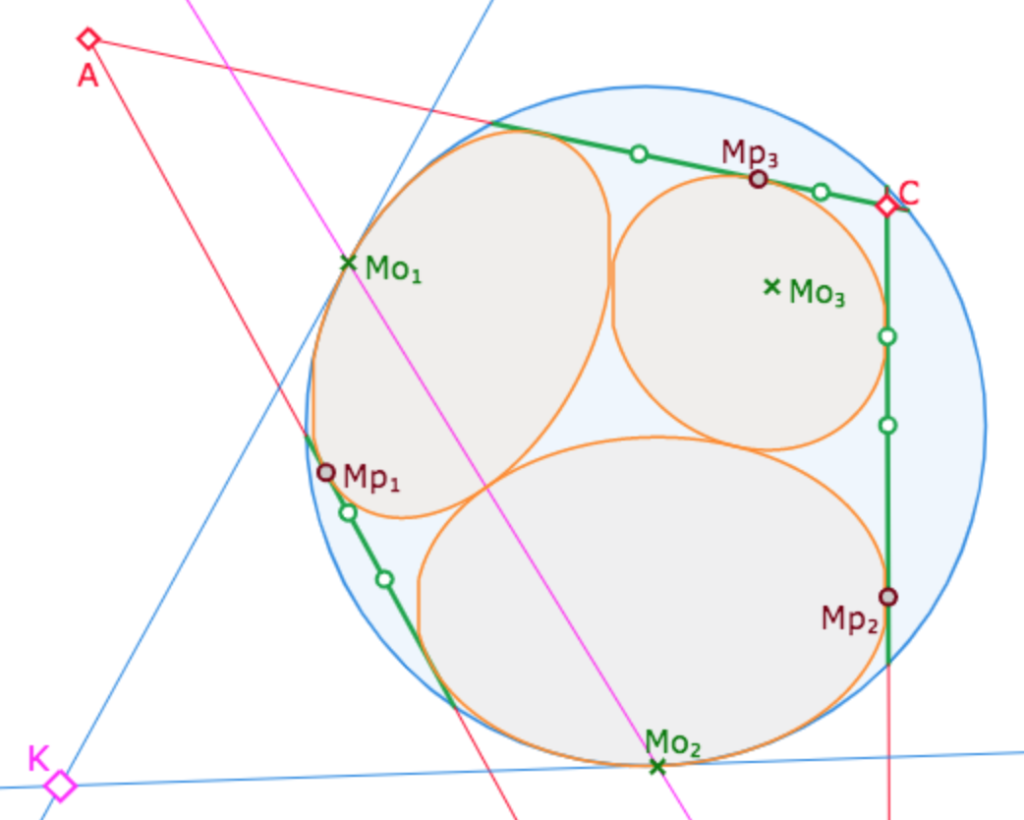
Poursuivons l’article de Beltrami, il continue en étudiant, « entre les circonférences géodésiques à centre réel et celles à centre idéal », un cas particulier, « celles qui ont leur centre à l’infini » – c’est-à-dire, dans la représentation KB, sur le cercle-limite.
Tout d’abord il fait la correspondance entre les horicycles centrés en l’unique point accessible depuis la pseudosphère et les parallèles à l’équateur sur la pseudosphère :
«D’autre part, les circonférences géodésiques dont le centre est à l’infini correspondent évidemment aux horicycles de la géométrie de Lobatchevsky. En conservant cette définition, nous pouvons donc dire qu’un système d’horicycles concentriques se transforme, par une flexion convenable de la surface, dans le système des parallèles de la surface de révolution engendrée par la ligne aux tangentes égales. »
Ensuite, reprenant ses calculs dans le cas général d’une surface à courbure constante négative, il montre une propriété de ces courbes, qui s’est avérée essentielle, chez Lobatchevsky et Bolyaï, pour construire l’équivalence entre la consistance de la géométrie hyperbolique et celle de la géométrie euclidienne (par les horisphères).
« En représentant de cette manière le système des circonférences géodésiques qui ont leur centre à l’infini au point \((u_0,v_0)\), le paramètre exprime l’intervalle constant entre une quelconque de ces circonférences et l’autre, l’une d’entre elles considérée comme fixe, et croît positivement à partir de la dernière vers le centre à l’infini. »
Voici une illustration de cet « l’intervalle constant ». On se donne deux points \(A\) et \(B\) sur la pseudosphère, que l’on envoie sur KB en \(A_{kb}\) et \(B_{kb}\). Sur le cercle limite, on prend un point \(I\) – qui correspond au point \((u_0,v_0)\) de la citation précédente. On construit les deux horicycles concentriques, de centre \(I\) passant respectivement par \(A_{kb}\) et \(B_{kb}\).
Pour construire la trace des horicycles sur la pseudosphère, on utilise un point \(Pt_{kb}\) qui permet de construire les points \(M_{kb}\) et \(N_{kb}\) issus de \(I\). Ensuite depuis un point \(U_{kb}\) du premier horicycle, on construit de même \(V_{kb}\). On vérifie ensuite l’égalité des distances sur la pseudosphère entre les points-retour \(M\) et \(N\) d’une part, et \(U\) et \(V\) d’autre part.
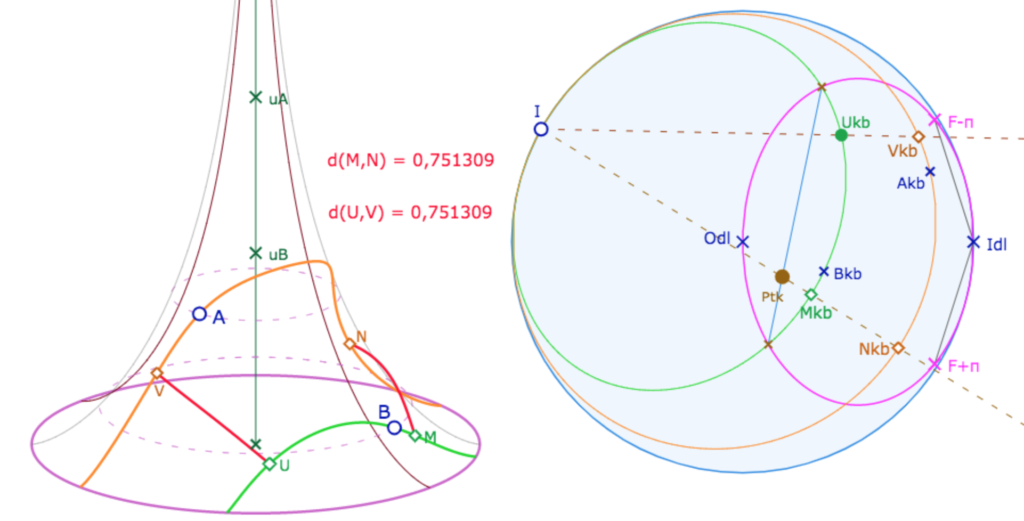
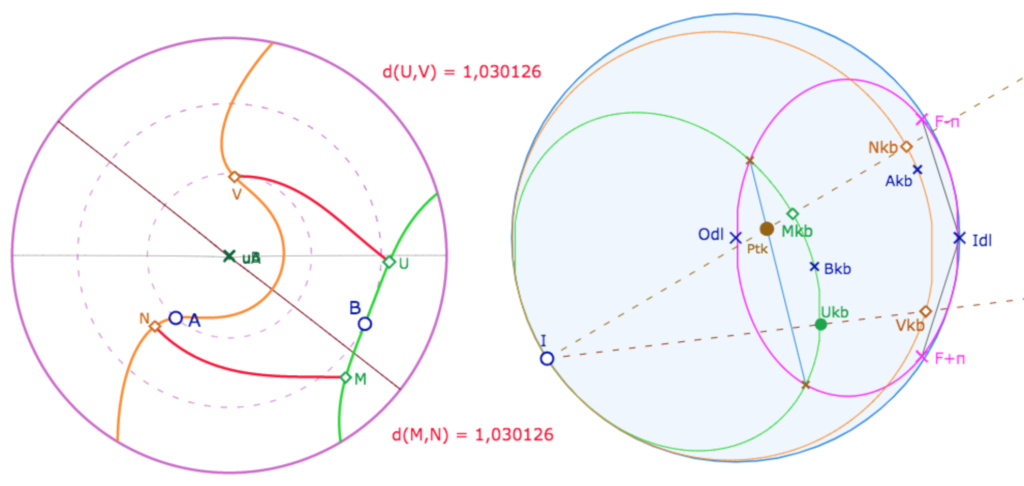
On n’a pas indiqué les distances sur KB, car la distance de KB est numériquement proportionnelle à celle sur la pseudosphère. En approchant I de la feuille suivante (ou précédente) de la feuille principale, on peut explorer des traces d’horicycles sur plusieurs feuilles comme ici :
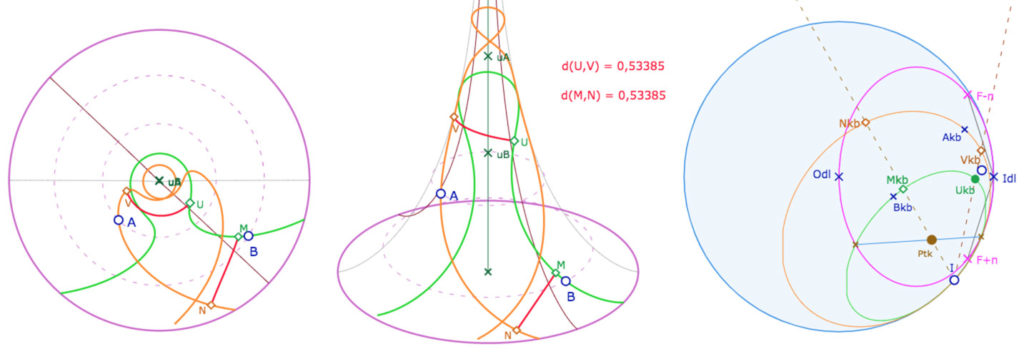
Manipulation de la figure
Modifier les points initiaux \(A\) et \(B\) out leurs altitudes. Jouer sur la position de \(I\) sur le cercle limite.
On peut déplacer \(Pt_{kb}\) (lent car c’est lui qui construit la trace des horicycles), ou encore \(U_{kb}\).
L’impossibilité de sortir de la représentation locale
Beltrami montre clairement, en faisant varier les distances entre deux horicycles concentriques, l’un restant fixe, que seule une partie du plan hyperbolique est représentée par la surface pseudosphérique, mais cela n’est pourtant pas explicitement mentionné, en particulier aucune conséquence élémentaire comme celles que nous avons simplement illustré dans les figures précédentes n’est abordée.
De même il n’aborde pas la question, en terme de représentation à l’intérieur de l’horicycle, de l’enroulement successif de la pseudosphère sur elle-même, alors que pour des réalisations concrètes, comme certaines figures que nous avons vues (le rêve de Coxeter par exemple), la question est importante.
On voit dans sa correspondance, qu’en fait Beltrami espérait que l’aspect local qu’il obtenait provenait uniquement de ce que, pour intégrer les surfaces, il a choisi le cas particulier d’une surface de révolution, et donc qu’il poursuivait ensuite son interprétation sur un cas particulier. Beltrami a toujours pensé qu’on trouverait peut-être une surface qui représenterait tout le plan hyperbolique. Il écrivait par exemple à Helmholtz :
« […] Ce passage, c’est-à-dire l’intégration des surfaces à courbure négative constante (pour le cas de la courbure positive c’est la même chose), n’a encore été faite que dans des cas très particuliers, que je sache. On ne connaît, parmi les formes infinies (dont mon petit modèle(*) me donne l’agréable spectacle) que la surface pseudosphérique peut prendre, que des surfaces de rotation et des hélicoïdes. Or ces formes spéciales ont un caractère commun, c’est de ne pouvoir servir au développement de la surface entière : il faut, pour les produire, couper la surface selon une ou deux lignes. Elles ne peuvent donc, même en supposant, pour les surfaces de rotation, que la surface absolue y soit enroulée un nombre infini de fois sur elle-même, reproduire l’infinité en tous sens de la surface absolue. »
Lettre à Helmholtz du 24 avril 1869
(*) vu la date, c’est est un modèle physique en carton, et c’est même celui dont nous avons donné la représentation photographique plus haut (réalisé le 22 avril)
C’est seulement en 1901, un an après sa mort, que Hilbert montrera que ce n’est pas possible :
«[…] on voit que [dans l’espace euclidien] il n’existe aucune surface à courbure constante négative dépourvue de la singularité analytique et partout régulière. En particulier, on doit répondre par la négative …à la question soulevée au début, à savoir qu’il n’existe pas dans l’espace une telle surface sur laquelle, à la manière de Beltrami, la géométrie du plan de Lobatchevsky se trouverait entièrement réalisée ».
Uber Flachen von konstanter Gaußscher Krummung », Transactions of the American matematical Society 2 (1901) – pp 87-99.
Cette page achève le travail initial proposé sur ce site autour de la pseudosphère. Depuis, plusieurs compléments sont disponibles sur les articles de blog. Le menu suivant (PSH) aborde néanmoins de nouvelles questions sur une autre pseudosphère, la pseudosphère hyperbolique, en particulier parce qu’elle recouvre, avec sa feuille principale, une plus grande part du plan hyperbolique.