Dans cette page, on ne propose qu’une toute première exploration de cette problématique relativement lourde pour un traitement dynamique général.
Introduction au régionnement
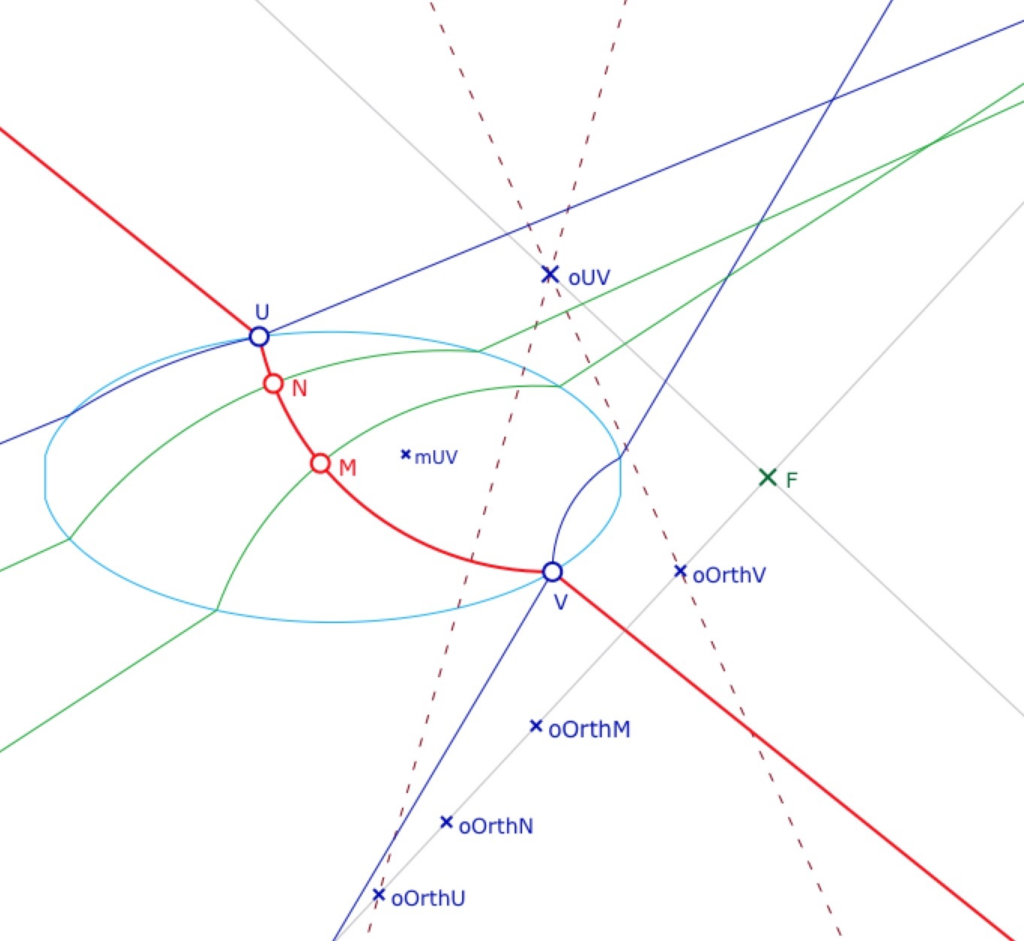
Puisque l’on s’intéresse aux droites rencontrant l’ellipse, on choisit de piloter cette droite par ses points sur l’ellipse, \(U\) et \(V\). En notant \(oUV\) le centre de l’arc de cercle intérieur à l’ellipse, les centres des arcs de cercle orthogonaux à \((UV)\) sont sur la perpendiculaire à \((FoUV)\) passant par \(F\). Les arcs orthogonaux limites sont de centre \(oOrthU\) et \(oOrthV\) intersection de cette perpendiculaire avec les médiatrices de \([UF]\) et \([VF]\) respectivement (en pointillé). On construit ainsi les H-droites limites (en bleu), H-orthogonales à \((UV)\) en \(U\) et \(V\), qui vont faire partie des frontières du régionnement.
Dans la suite on notera \(sU\) et \(sV\) les autres intersections que \(U\) et \(V\) de ces droites avec l’ellipse (illustré ci-dessous).
Les autres frontières qui vont intervenir dans le régionnement sont les parties extérieures à l’ellipse (demi-droites roses) des perpendiculaires euclidiennes à la droite \((UV)\) en \(U\) et \(V\).
On note \(soU\) et \(soV\) les autres points d’intersection de ces droites avec l’ellipse.
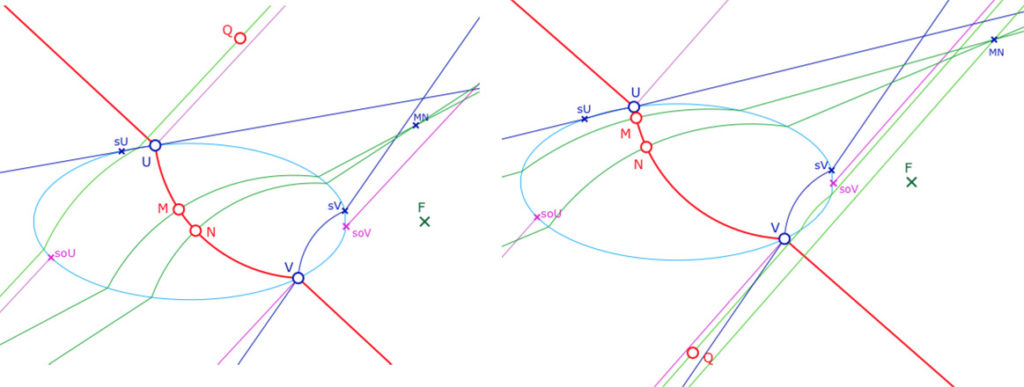
Pour se familiariser avec les questions que nous allons aborder dans la suite, la figure suivante permet de manipuler la construction de base présentée ici. Un point \(Q\) est aimanté par les quatre demi-droites vertes constituant les deux perpendiculaires en \(M\) et \(N\), à 100 pixels donc pas nécessairement bloqué sur ces positions comme on le voit ci-dessus, à gauche comme à droite. On peut donc déplacer \(Q\) sur ces demi-droites mais aussi en sortir. Comme on le voit dans les deux illustrations, de \(Q\) on mène aussi une (autre) perpendiculaire à \((UV)\) quand elle existe.
Mais cette figure est surtout présentée pour explorer la partie où il y a trois perpendiculaires issues du point d’intersection \(MN\) des deux H-perpendiculaires à \((UV)\) en \(M\) et \(N\), et manipuler la figure pour visualiser la nécessité de construire l’enveloppe de la perpendiculaire en \(M\) pour délimiter certaines régions. On notera que la troisième perpendiculaire peut être euclidienne, tout en coupant aussi l’ellipse autour du point \(V\). (non illustré ci-dessus à droite en \(MN\) mais illustré avec le point \(Q\) placé dans une région où il y a une perpendiculaire euclidienne).
Premières explorations du régionnement en dehors de l’ellipse pour l’orthogonalité à \((UV)\)
• On peut déplacer \(M\) et \(N\) sur l’arc entre \(U\) et \(V\), mais aussi \(Q\) comme indiqué dans la page précédente.
• On peut aussi déplacer \(U\) et \(V\) pour tester de nombreuses variantes du régionnement.
• Quelle est la frontière de la région (à l’ouverture de la figure) à deux – ou trois – perpendiculaires au dessus du point \(F\) ?
Frontière de la partie d’où on mène deux perpendiculaires (et parfois trois)
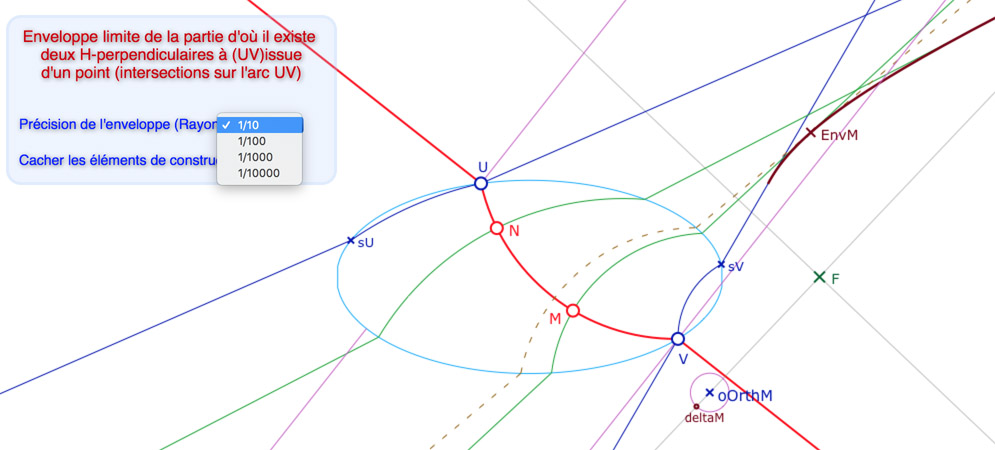
Dans la figure suivante, on construit l’enveloppe de la perpendiculaire passant par \(M\). Pour cela on fait l’intersection en la perpendiculaire en \(M\) et en un point \(M+\delta M\) géré par un pop-up (pour voir le cercle et la droite en \(M+\delta M\), en pratique on prendra la précision la plus grande). On obtient le point \(EnvM\) dont on fait le lieu quand \(M\) varie sur l’arc \((UV)\).
Dans l’illustration de ci-dessous, la partie à la fois au dessus de l’enveloppe, à droite de la H-droite \((VsV)\) et en dessous de la H-droite \((UsU)\) est une partie non bornée qui contient tous les points d’où on peut construire deux perpendiculaires hilbertiennes à \((UV)\) – tous, pour cette configuration – et, à droite de la demi-droite rose d’origine \(soV\), les points d’où on peut construire en plus une perpendiculaire euclidienne. On se propose dans la suite de colorier dynamiquement ce type de partie.
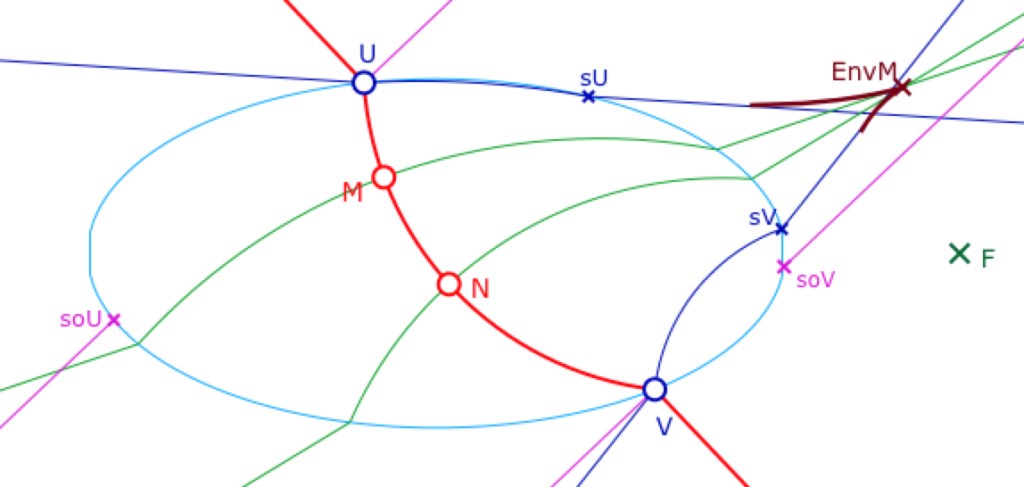
On souhaiterait, dans la suite, colorier dynamiquement ce type de partie. La colorisation dynamique devra rendre compte des configurations comme celle ci-contre.
Dans ce cas la région d’où on peut mener deux H-perpendiculaires est une toute petite région, ici au dessus de la droite \((UsU)\) et en dessous du lieu.
Par ailleurs, cette partie à deux H-perpendiculaires étant à gauche de la demi-droite d’origine \(soV\), il est clair qu’il n’y a pas, dans cette configuration, de possibilité de tri-perpendiculaires issue d’un point.
Exploration autour de l’enveloppe de la perpendiculaire en \(M\) à \((UV)\)
Le réglage de la précision est grossier à l’ouverture pour voir la droite en \(M+\delta M\). Ajuster ensuite à un réglage plus fin.
Manipuler \(U\) et \(V\) pour visualiser les différentes formes de l’enveloppe de \(M\).
Colorisation dynamique de la partie 2H et 2H1E
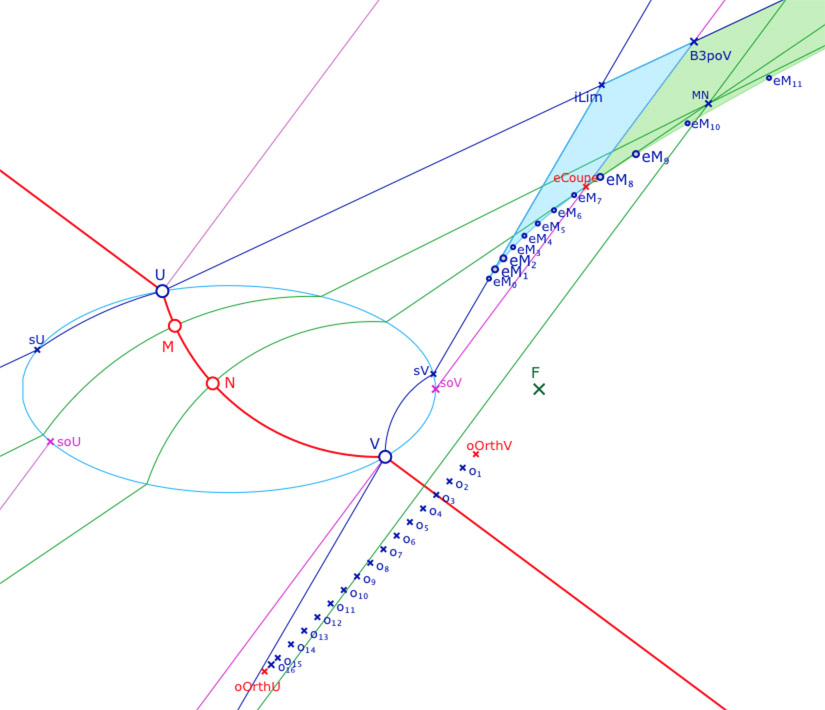
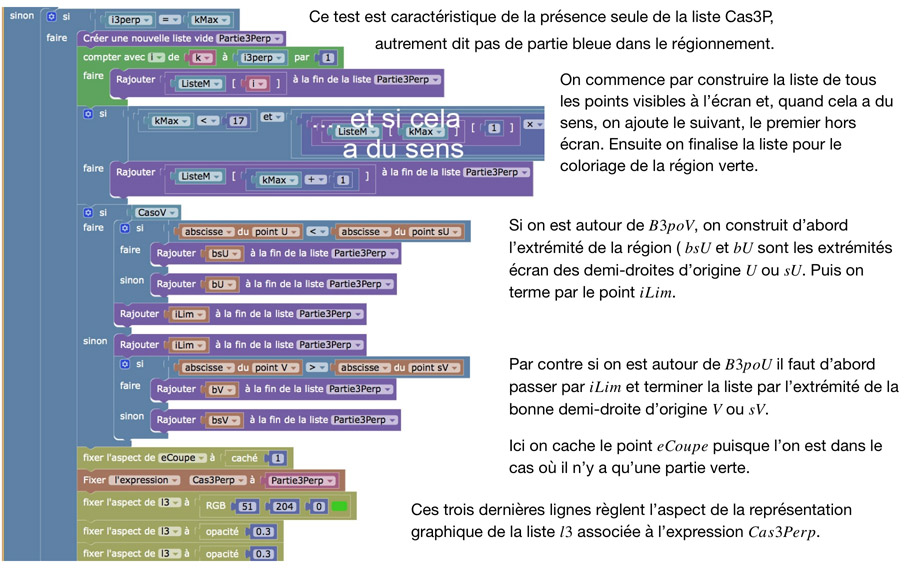
Il s’agit de construire les frontières du régionnement des parties ayant deux H-perpendiculaires (2H) et celles avec 3 perpendiculaires (2H1E)dans un contexte technique spécifique, celui de liste de segments. Pour cela on se donne 16 points entre les deux centres limites \(oOrthU\) et \(oOrthV\) et on applique la construction vue précédemment à ces centres qui donnent 17 points \(eM_0\) à \(eM_{16}\) (le point \(eM_0\) est obtenu à partir d’un point plus proche de \(oOrthU\)). La frontière entre la partie 2H (bleue) et la partie 2H1E (verte) est régie par les points suivants :
• \(iLim\) l’intersection entre les droites \((VsV)\) et \((UsU)\) .
• \(B3poV\) (pour Borne pour 3 perp sur (VsoV) – ci-contre à l’intersection de \((UsU)\) et \((VsoV)\).
• \(B3poU\) – illustré ci-dessous à l’intersection de \((VsV)\) et \((UsoV)\).
Le type de région – 2H ou 2H1E – est défini par la position de ces points entre eux : ci-dessus \(B3poV\) est à droite de \(iLim\), il y a donc une partie bleue et une verte alors que ci-dessous \(B3poU\) est à gauche de \(iLim\) et donc toute la partie est verte (en fait car \(soU\) est d’abscisse inférieure à celle de \(sU\)).
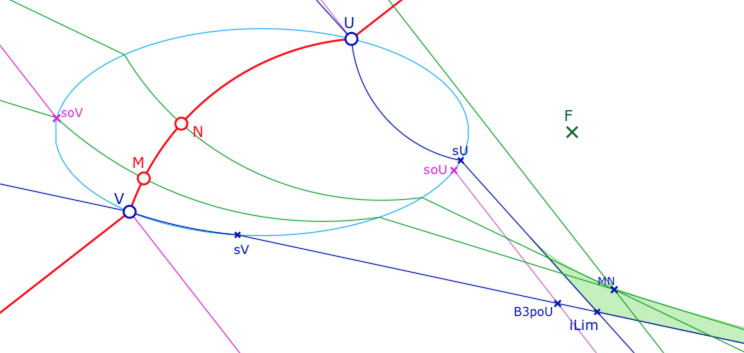
Exemples de configurations où l’enveloppe est bornée
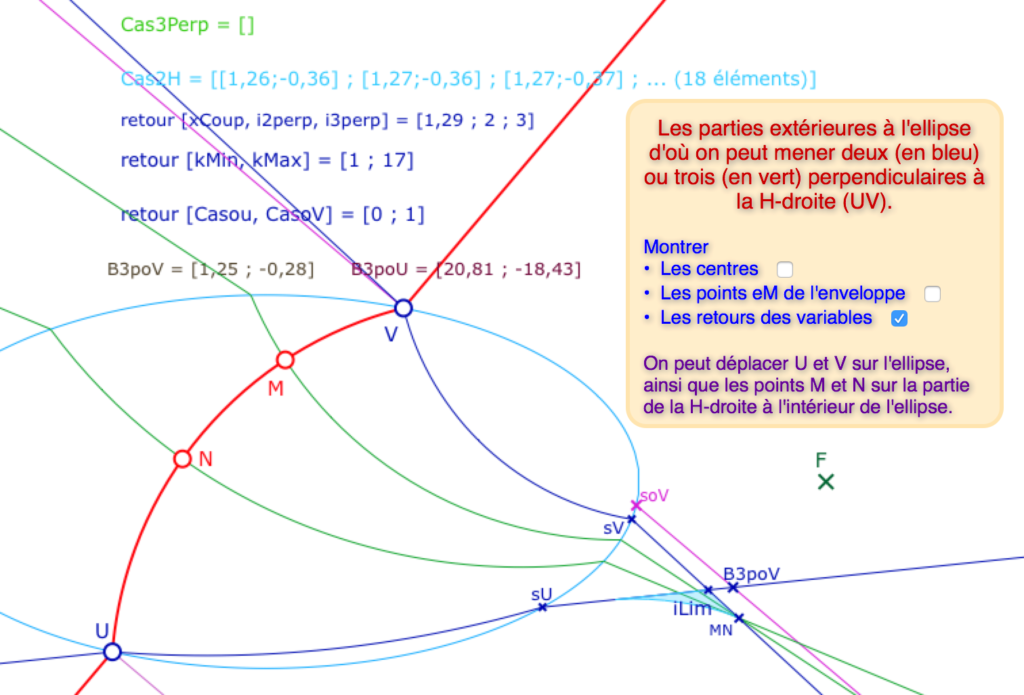
Ci-contre détail des variables que l’on peut choisir d’afficher sur la prochaine figure disponible.
Sens des variables :
• Listes des parties 2H1E (3Perp) et 2H.
• \(kMin\) et \(kMax\) sont les bornes de la présence des \(eM_i\) à l’écran.
• Utilise-t-on \(B3poV\) ou \(B3poU\) ? Par les booléens \(CasoU\) et \(CasoV\).
• x\(xCoup\) : abscisse du point de coupe entre les indices \(i2perp\) et \(i3perp\) des points \(eM_i\). N’est pas réactualisé quand \(Cas3Perp\) devient vide.
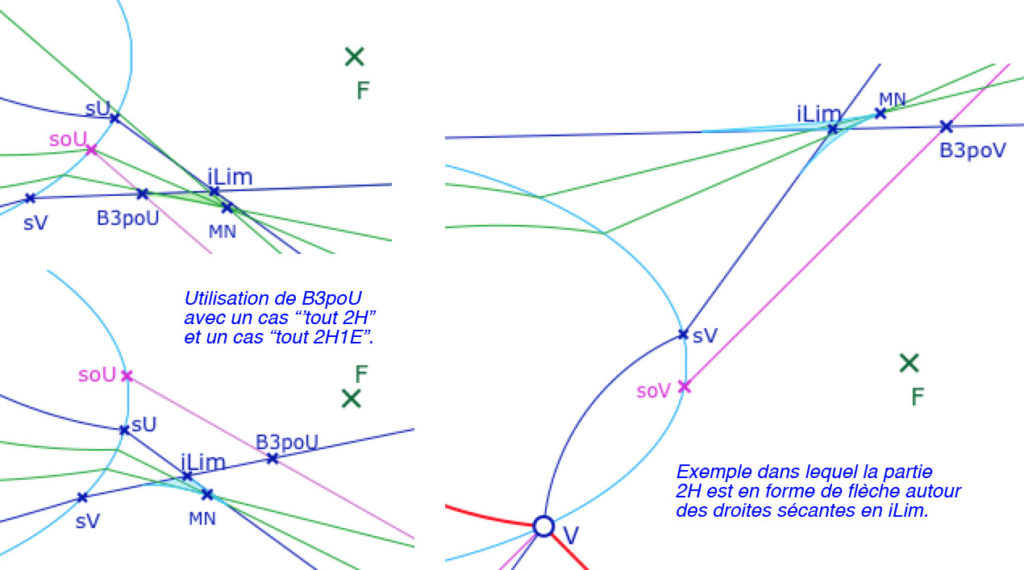
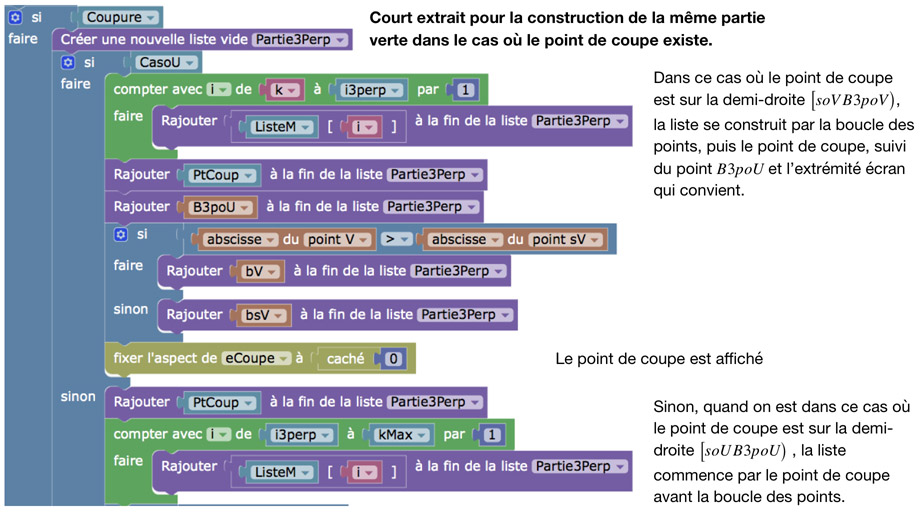
Court extrait de la fonction LesListes2P3P : cette fonction fixe l’expression Cas3Perp (illustré dans cet extrait) et en même temps renvoie l’expression Cas2H. Tous ces codes sont dans cette expression (même si la liste est vide).
• On observera l’ordre différent des points \(eM_i\) selon leur emplacement (ordonnées croissantes ou décroissantes).
• On peut déplacer l’ellipse. Toutefois,les parties coloriées ne sont calculées que si elles sont visibles à l’écran.
Tout le code de cette figure (même celui de Cas3Perp) est dans l’expression Cas2H. Pour consulter le code, utiliser cette figure hors contexte de restrictions. Elle s’ouvre dans un autre onglet.
Exemple statique du régionnement de toute la partie extérieure à l’ellipse
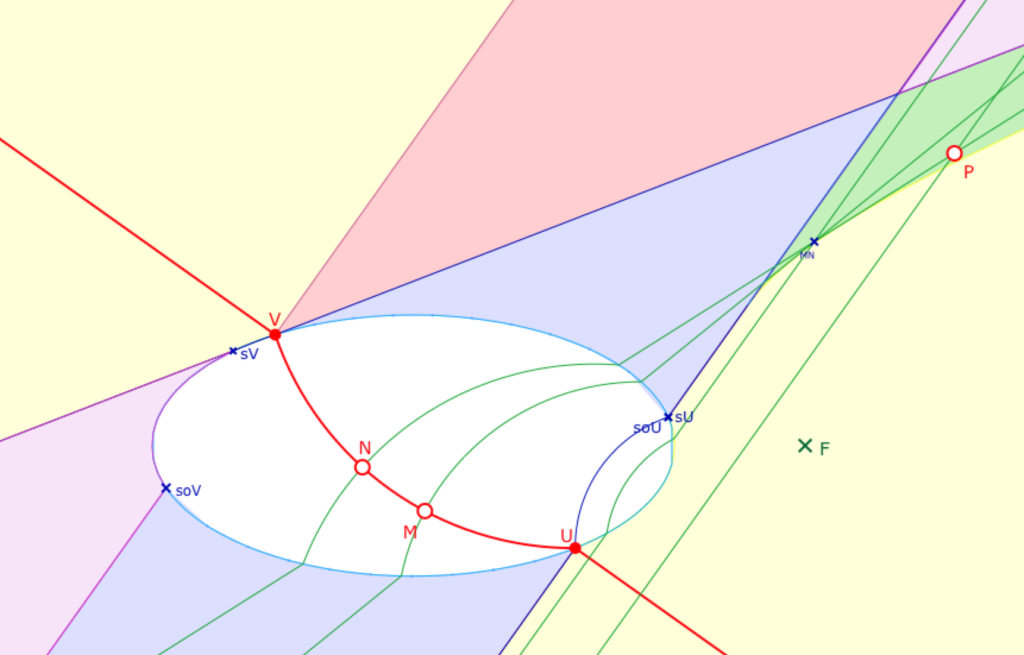
Étant donnée une droite coupant l’ellipse, il peut y avoir jusqu’à six types différents de régionnement vis à vis de l’orthogonalité à cette droite.
Sur la figure suivante, on a fixé les deux points \(U\) et \(V\) de telle façon que ces six types soient bien présents. On peut alors choisir l’affichage individuel de chacun d’eux. La figure ci-dessus correspond aux parties 4 et 6, traitées – partiellement – dynamiquement. Comme dans une figure précédente, le point \(P\) est aimanté par les deux demi-droites de la H-perpendiculaire à \((UV)\) passant par \(N\).
Dans cette figure on ne peut que déplacer \(M\), \(N\) et \(P\) et désactiver les cases à cocher.
On n’a pas détaillé le code des quatre autres parties. Seules celles qui sont au contact des parties 4 et 6 demandent de l’attention. Ci-contre, le cas où l’on déplace légèrement le point \(V\) pour que les points de l’ellipse \(sU\) et \(soU\) coïncident : la région bleu claire à deux H-perpendiculaires disparait, et il ne reste plus qu’une seule région rouge, sans aucune perpendiculaire. Même si une procédure générique est utilisée pour le contour de l’ellipse (la procédure «morceau» ci-dessous), le nombre de situation est si important que la situation reste trop lourde à traiter pour que la figure dynamique produite reste réellement manipulable. En pratique, il faudrait reprendre le coloriage de manière différente pour arriver à le rendre effectivement dynamique, on ne peut guère aller beaucoup plus loin avec cette démarche.
En particulier, la partie à deux H-perpendiculaires avec un point de rebroussement n’est – pour le moment – pas encore assez caractérisée pour être intégrée dans dans un processus de régionnement dynamique. C’est la raison pour laquelle cette partie s’arrête ici.
Régionnement à l’intérieur de l’ellipse
Le contexte ici est différent de la section précédente, et plus simple à traiter. On se donne une H-droite \((AB)\) avec \(A\) et \(B\) à l’intérieur de l’ellipse, et un point \(M\), lui aussi à l’intérieur de l’ellipse. Le régionnement de l’ellipse consiste à colorier les cas où il n’y a aucune perpendiculaire, deux perpendiculaires – dans ce cas c’est une hibertienne et une euclidienne car il ne peut y avoir deux hilbertiennes, et le cas où il n’y a qu’une seule perpendiculaire euclidienne.
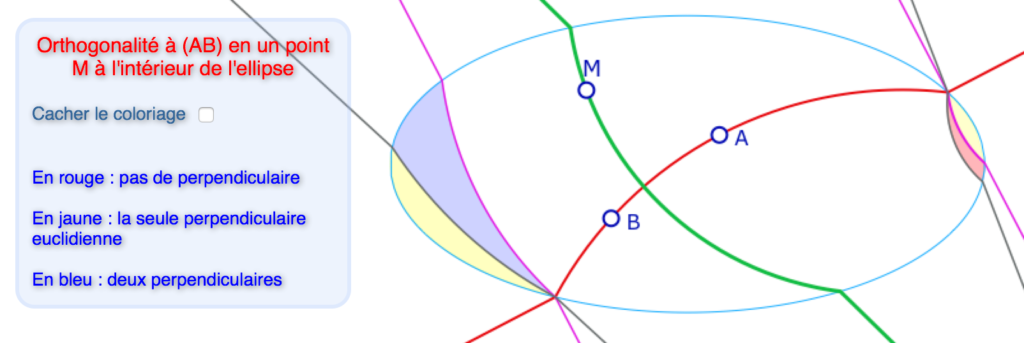
On a choisi de ne pas colorier le cas le plus trivial, celui où il n’y a qu’une perpendiculaire hilbertienne car c’est, en général, la plus grande partie à l’intérieur de l’ellipse comme on le voit sur cette illustration. La H-orthogonalité est l’orthogonalité euclidienne de deux cercles : celui circonscrit à \(A, B\) et \(F\) et celui passant par \(M, F\) et orthogonal au précédent.
Les trois autres régions sont des parties de l’ellipse qui partent de ses points d’intersection avec la H-droite \((AB)\).
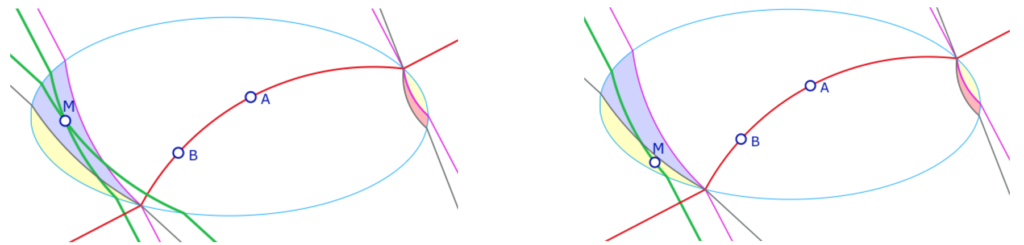
La partie à une seule perpendiculaire euclidienne peut être assez importante, ici avec deux droites \((AB)\) différentes.
En fait la figure finale n’est pas très opérationnelle … elle n’est correcte qu’à 60% des cas. La rédaction a été annulée et fera partie d’une prochaine mise à jour ….
Un peu désolé … mais temporaire …