Les systèmes de Steiner
Même si nous n’allons regarder qu’un cas très particulier des systèmes de Steiner, plaçons notre cas particulier dans son contexte général. On appelle système de Steiner \(S(p, k,n)\) un ensemble de \(n\) éléments et un ensemble \(T\), de sous ensembles de \(S\), à \(k\) éléments appelés blocs tels que tout sous-ensemble de \(S\) de \(p\) éléments est contenu dans un et un seul bloc. Les systèmes de Steiner sont liés, entre autres, aux premiers groupes sporadiques, les groupes de Mathieu.
Pour ce qui nous concerne ici, on ne s’intéresse qu’au cas p=2. En effet, dans ce cas, cette définition correspond à l’axiome d’incidence de la géométrie pour une géométrie finie où les blocs sont les droites. Par exemple, dans un plan projectif fini d’ordre \(k\), chaque droite contient \(k+1\) points et par chaque point il passe aussi \(k+1\) droites. On montre alors que c’est un \(S(2,k+1,k^2+k+1)\).
En enlevant un bloc et tous les points de ce bloc à \(S\), on enlève en fait la «droite de l’infini». Il reste alors un plan affine d’ordre \(k\). Ce plan comprend \(k^2\) points, \(k^2+k\) droites, chaque droite comporte k points. C’est un \(S(2,k,k^2)\).
Ainsi le plus petit plan projectif est \(S(2,3,7)\) associé au corps \(\displaystyle \frac{\mathbb{Z}}{2\mathbb{Z}}\) et \(S(2,3,9)\) est le plan affine associé à \(\displaystyle \frac{\mathbb{Z}}{3\mathbb{Z}}\). En effet on montre qu’il n’existe qu’un seul \(S(2,3,7)\) et un seul \(S(2,3,9)\).
Les systèmes de triplets de Steiner
Dans cette page, on s’intéresse aux systèmes de triplets de Steiner, c’est-à-dire les \(S(2,3,n)\) que l’on note STS(n). On sait alors (Kirkman – 1847) qu’un système \(S(2,3,n)\) existe si et seulement n est congru à 1 ou à 3 modulo 6. Il existe donc ainsi, outre les \(S(2,3,7)\), \(S(2,3,9)\), des systèmes de triplets de Steiner \(S(2,3,13)\) et S(2,3,15) pour les plus petites valeurs de \(n\).
Le nombre de blocs de \(S(2,3,n)\) est \(\displaystyle \frac{n(n-1)}{6}\). On a, pour les deux premiers systèmes non triviaux (car S(2,3,3) = {123})
\(S(2,3,7)\) = {123, 137, 156, 235, 267, 346, 457}. C’est une configuration 73, donc le plan projectif à 7 points et 7 droites .
\(S(2,3,9)\) = {123, 147, 159, 168, 249, 258, 267, 348, 357, 369, 456, 789} : plan affine de 9 points et 12 droites.
Le plan affine d’ordre 3 dans un modèle octogonal de STS(9)
Les deux modèles proposés dans la suite de cette page, pour STS(9) et STS(13) proviennent
de l’ouvrage de Burkard Poster « A geometrical picture book » – Springer – 1998
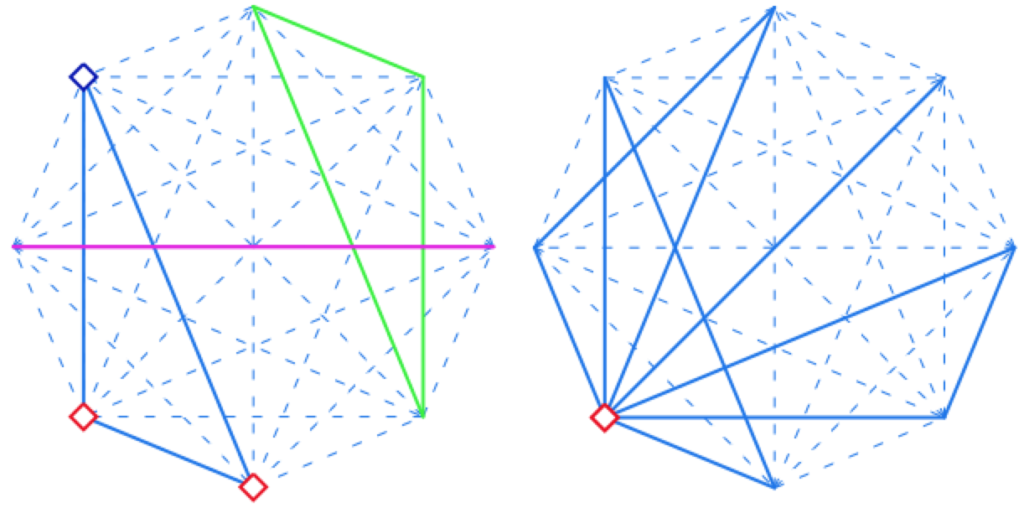
Le modèle ci-contre de triplets de Steiner est représenté par les huit sommets d’un octogone régulier et de son centre.
Les droites sont les quatre diamètres et huit triangles, isométriques, en rotation d’un générateur (bleu ci-contre).
L’illustration de gauche montre un faisceau de trois droites parallèles. Celle de droite, le faisceau des quatre droites issues d’un point.
Deux exemples des médianes d’un triangle dans ce modèle
Soient \(ABC\) un triangle du plan affine. On note \(I, J, K\) les milieux des côtés, c’est-à-dire le troisième point de chaque droite du triangle, soit respectivement, dans l’illustration de gauche, les triangles euclidiens \(ABI, BCJ, CAK\).
Les médianes (toujours à gauche) sont les droites représentées par le diamètre \(CWI\), et les deux triangles \(AUJ\) et \(BKV\). Sur l’illustration de droite, le côté \([AB]\) est un segment euclidien (diamètre), la médiane \((CI)\) est encore un segment. Les deux autres médianes sont les triangles \(AJU\) et \(BVK\).
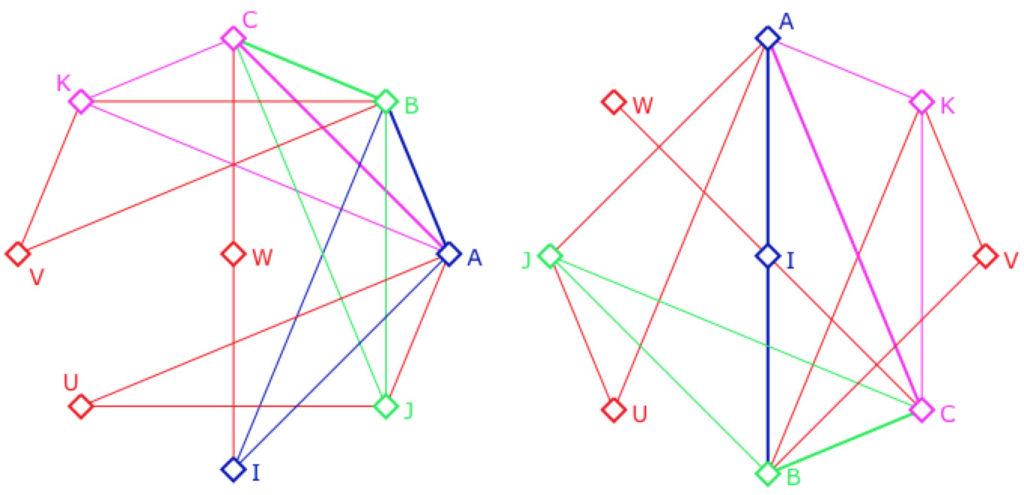
Dans ces deux illustrations les médianes du triangle \(ABC\) sont trois droites parallèles comme
on l’a montré (page précédente) dans le cas général des plans affines d’ordre 3.
Aspect euclidien du plan affine d’ordre 3 dans ce modèle
On l’a dit, tous les triangles sont rectangles, et les cercles, ayant 4 points, sont aussi des carrés. Reprenons, sur cette question des carrés, l’exemple déjà développé dans la page précédente.
Comme le modèle euclidien borné, on voit, dans un premier temps, que ce modèle est «conforme au centre». En effet ci-dessous, sur l’illustration de gauche, le carré ABCD de centre O est représenté par un carré avec les angles droits. On remarque que le carré des milieux IJKL est aussi de même centre, et est aussi dans une représentation conforme.
Les trois droites (AB), (CD) et (LJ) sont parallèles et ont donc une perpendiculaire commune, à savoir la droite (IK). En effet, par exemple, \((IO)\) est une médiatrice des deux triangles \(ABC\) et de \(CDA\).
Par ailleurs, comme tout point d’une droite est milieu des deux autres, on peut inverser les rôles de \(I\) et \(A\) dans l’illustration de gauche :
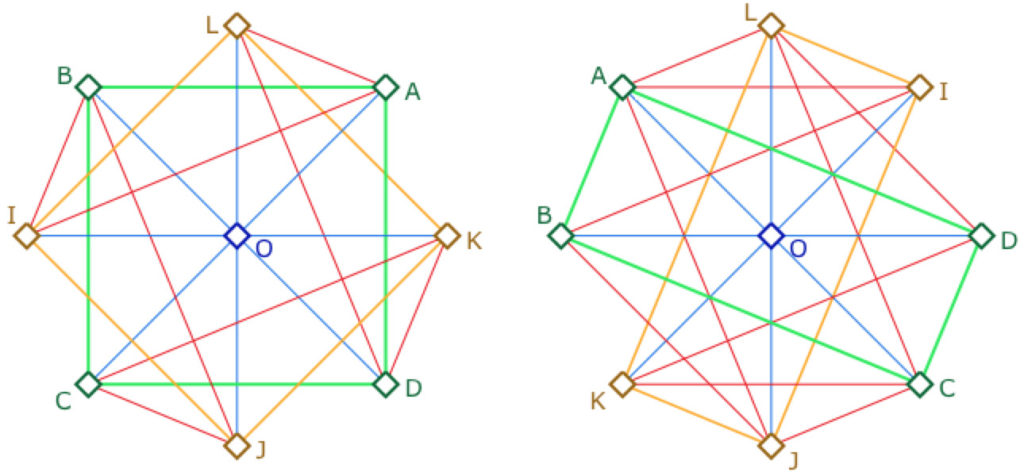
C’est ce que l’on a fait dans l’illustration de droite, où \(ABCD\) est encore toujours un carré de centre \(O\), ainsi que le quadrilatère des milieux \(IJKL\). La représentation est toujours conforme, tous les angles en chaque sommet sont droits dans le modèle, tout comme leurs diagonales en \(O\), même si ces carrés sont désormais représentés par des rectangles.
Par contre \(AKCI\) à gauche n’est pas un carré , mais en est un à droite. \(ALJC\) est un rectangle non carré dans les deux illustrations, tout comme \(DKBI\).
La figure suivante propose une version dynamique du plan affine dans les trois modèles, celui-ci, et les deux présentés dans dans la page précédente du menu, avec les faisceaux des droites parallèles et des droites concourantes.
Contient à la fois les faisceaux de droites parallèles et les faisceaux de droites concourantes (faire \(B=A\))
Réalisation d’un modèle dynamique du STS(13) hyperbolique
Il existe deux STS(13). Ils ont 26 blocs (13×12/2). Ces deux systèmes peuvent s’écrire :
STS13a = {(1,2,3), (1,4,5), (1,6,7), (1,8,9), (1,10,11), (1,12,13), (2,4,6), (2,5,8), (2,7,9), (2,10,12), (2,11,13), (3,4,10), (3,5,6), (3,7,11), (3,8,13), (3,9,12), (4,7,12), (4,8,11), (4,9,13), (5,7,13), (5,9,10), (5,11,12), (6,8,12), (6,9,11), (6,10,13), (7,8,10)}
Le second a les mêmes 14 premiers blocs, jusqu’à (3,7,11). Sur les 12 suivants, 6 sont communs.
STS13b = {(1,2,3), (1,4,5), (1,6,7), (1,8,9), (1,10,11), (1,12,13), (2,4,6), (2,5,8), (2,7,9), (2,10,12), (2,11,13), (3,4,10), (3,5,6), (3,7,11), (3,8,12), (3,9,13), (4,7,12), (4,8,13), (4,9,11), (5,7,13), (5,9,10),(5,11,12), (6,8,11), (6,9,12), (6,10,13), (7,8,10)}.

C’est le second système qui est un plan hyperbolique fini.
Il comporte donc 13 points et 26 droites. Chaque droite ayant trois points, ces 3×26 points se répartissant sur 13 points du plan, par chaque point du plan il passe 6 droites.
A nouveau, chaque droite ayant 3 points ces 6 droites peuvent être produites par deux générateurs à partir de chaque point du plan.
Un modèle possible est alors une représentation à partir des sommets d’un polygone régulier à 13 sommets et les deux générateurs ci-contre(*). En faisant cela à chaque sommet, on a ainsi les 26 droites.
(*) Burkard Poster, « A geometrical picture book » – Springer – p 24
Les sommets ne sont pas indexés (pas du tout) nécessairement par le numéro associé aux éléments du bloc. Il faut élaborer des correspondances.
Voici celle retenue pour réaliser les figures suivantes, parmi de très nombreuses possibilités bien entendu. Cela transforme la représentation par le graphe complet du polygone régulier à 13 sommets et ses diagonales en modèle géométrique du STS13b, où les droites sont des triangles :
(1, A), (2, C), (3, H), (4, B), (5, K), (6, L), (7, F), (8, I), (9, G), (10, J), (11, M), (12, E), (13, D).
On déplace simplement les deux points rouges ronds. Le troisième point (carré) de la droite est construit d’après les blocs de STS13b.
Les parallèles de STS(13)
Par un point, il passe trois parallèles à une droite donnée
Choisir la droite par \(A\) et \(B\). Vérifier que pour tout \(M\) hors de \(\{A, B, I \}\),
il y a toujours trois droites passant par \(M\) ne rencontrant pas la droite \((AB)\).
Les faisceaux de droites
On déplace simplement le point \(M\).
Qu’est-ce qu’un plan hyperbolique fini d’incidence ?
Dans le cas où il n’y a pas d’orthogonalité (différence entre droites parallèles et droites ayant une perpendiculaire commune), pour éviter les situations marginales sans intérêt, on ajoute une contraint ensemblistes à la simple incidence (définie par l’appartenance d’un point à une droite).
On appelle sous espace \(X\) d’une géométrie finie un ensemble de points tel que si deux points \(A\) et \(B\) sont dans \(X\), alors la droite \((AB)\) est aussi contenue dans \(X\).
Un plan fini d’incidence (un ensembles de points et un ensemble de droites donnés) est dit hyperbolique si et seulement si :
• Par un point n’appartenant pas à une droite il existe au moins deux droites non sécantes à cette droite (définition usuelle des droites parallèles).
• Tout sous espace contenant un triangle est le plan tout entier.
Contrainte de non dégénérescence propre aux structures finies :
tout sous espace contenant un triangle est le plan tout entier.
On se donne un triangle \(ABC\). On appelle \(I, J\) et \(K\) les troisièmes points de \((AB), (BC)\) et \((CA)\)respectivement. On construit les droites passant par un sommet et le troisième point de la droite opposée, droites qui ne sont plus a priori des médianes comme dans \(STS9\) car il n’y a rien pour définir le milieu. On nomme enfin \(P, Q\) et \(R\) les troisièmes points de ces droites, soit les droites «triangles-euclidien» \(AJP, BKQ, CIR\).
Dans le meilleur des cas – à gauche – on a 9 des 13 points placés, il reste 4 points à atteindre comme troisième point de droites passant par deux des points déjà construits.
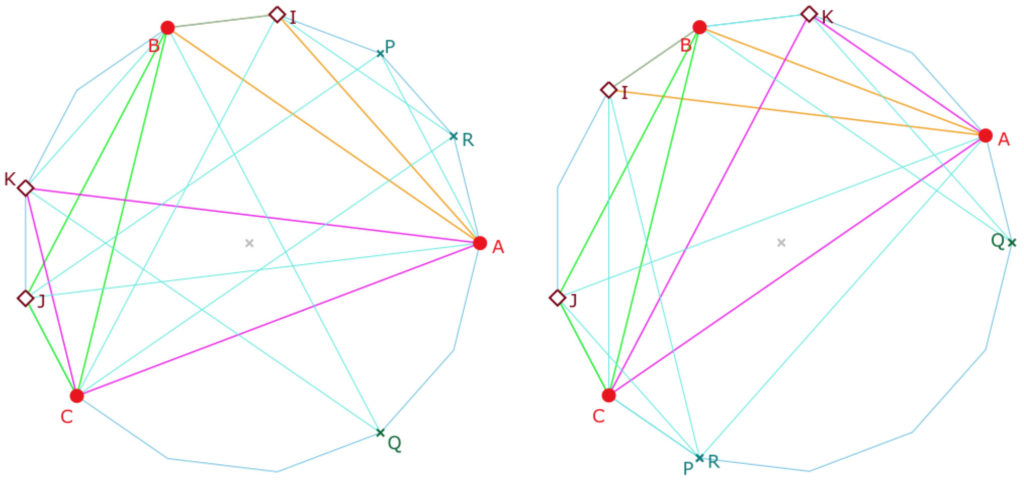
Dans d’autres cas, deux des points \(P, Q\), et \(R\) sont confondus. En général on a néanmoins 4 points consécutifs du polygones atteints, sauf dans un cas, (à une rotation prés, ici on a choisi de travailler avec \(C\) fixe). C’est le cas de l’illustration de droite.
Or si on se reporte à la figure du faisceau issu d’un point, la droite nommée \((MR_1R_2)\) permet de construire \(R_2\) à partir de \(M\) et \(R_1\). Si on dispose de 4 points consécutifs qui représentent respectivement \(R_1, M\), puis \(M_2\) et \(T_2\) du faisceau de droites issues de \(M\), on construit \(R_2\) et en itérant, avec ce seul type de droite, on assure la réalisation de la contrainte. C’est aussi le cas ci-contre en commençant par \(A\) et \(Q\). On construit un point avant \(P(=R)\). On a alors 4 points consécutifs, c’est fini, on assure de remplir le plan.
Présentation de la figure suivante sur cette contrainte
Dans cette figure, on a ajouté les trois droites construites à partir du triangle \(IJK\). Dans le meilleur des cas, on ajoute trois points (\(U, V\) et \(W\)), et donc, toujours dans le meilleur des cas, il ne reste qu’un point à obtenir. D’après le procédé décrit juste avant, la contrainte est réalisée. C’est le cas de l’illustration de gauche.
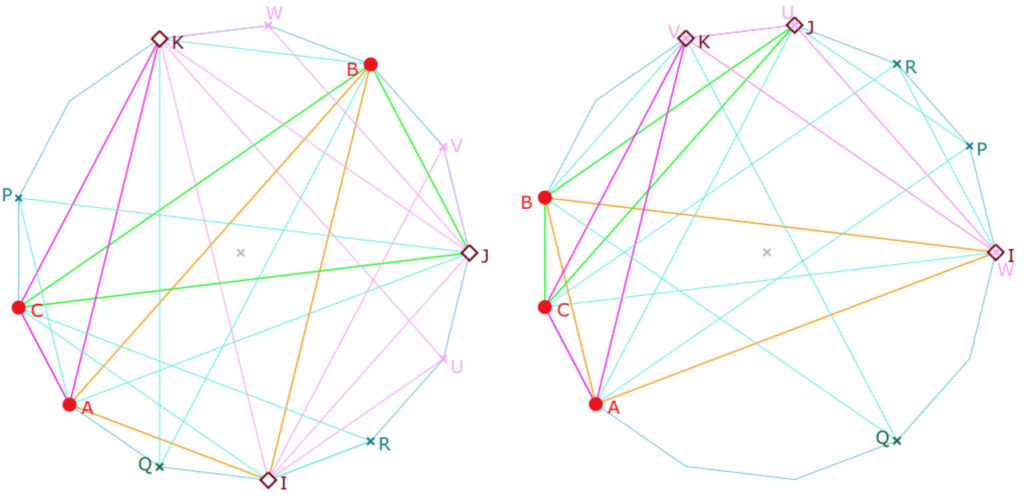
Mais il y a plusieurs situations où l’ajout de ces trois droites n’ajoute pas de points au sous espace en construction. C’est en particulier le cas (mais pas seulement) quand \(I, J, K\) sont STS13-alignés comme dans l’illustration de droite : alors \(U, V\) et \(W\) sont sur \(J, K\) et \(I\). Quoi qu’il en soit, il y a toujours 4 points du sous espace sur des sommets consécutifs du polygone, et donc on assure que le sous espace est le plan tout entier.
Dans la figure suivante, on a déjà placé ces 12 points, dont certains éventuellement confondus : \(A, B, C, I, J, K, P, Q, R\) et enfin \(U, V, W\). Vous disposez de deux points M et N pour ajouter une autre droite MNE et valider, en plaçant la droite à différents endroits pour simuler de nouvelles droites, que l’on peut compléter le sous espace en le plan tout entier.
Vous pouvez agir sur les hypothèses \(A, B\) et \(C\). Puis déplacer \(M\) et \(N\) pour valider que vous ajoutez les points manquants, un à un.
La figure d’ouverture est placée dans une des configurations les moins favorables.