Bien entendu, il faut avoir lu la première page sur le plongement projectif de Bachmann pour aborder celle-ci. Le figures utilisées dans cette page sont soit trop grandes, soit accompagnées de longs commentaires pour être manipulées dans la page elle-même. On renvoie donc systématiquement à la manipulation de chaque figure en ligne dans un autre onglet pour que cela soit plus confortable d’utilisation. D’où aussi les commentaires parfois détaillés de ces figures pour être un peu autonome.
Quelques considérations techniques préalables
On rappelle que l’objectif de ces pages sur le plongement projectif est seulement d’illustrer, dynamiquement, la démarche générale de Bachmann dans l’environnement du modèle hyperbolique du disque de Poincaré. Dans ce contexte, pour aborder plus finement les concepts de Bachmann, on va aller plus en détail sur certains résultats qui, s’ils n’ont pas d’intérêt théoriques particuliers, vont être utiles pour la mise en œuvre des figures.
Le lieu des centre des droites tangentes à un cercle hyperbolique
On commence par quelque chose qui semble bien éloigné de la problématique initiale, mais un peu plus loin, nous serons amené à utiliser des droites hyperboliques tangentes au cercle \(C_{uv}\). Voici une synthèse de la construction du lieu des centres euclidiens de ces droites. Une page de blog reviendra … un jour … sur ce résultat, par ailleurs assez classique, et dont une variante est parfois utilisée, par exemple dans le cadre des polygones réguliers hyperboliques.
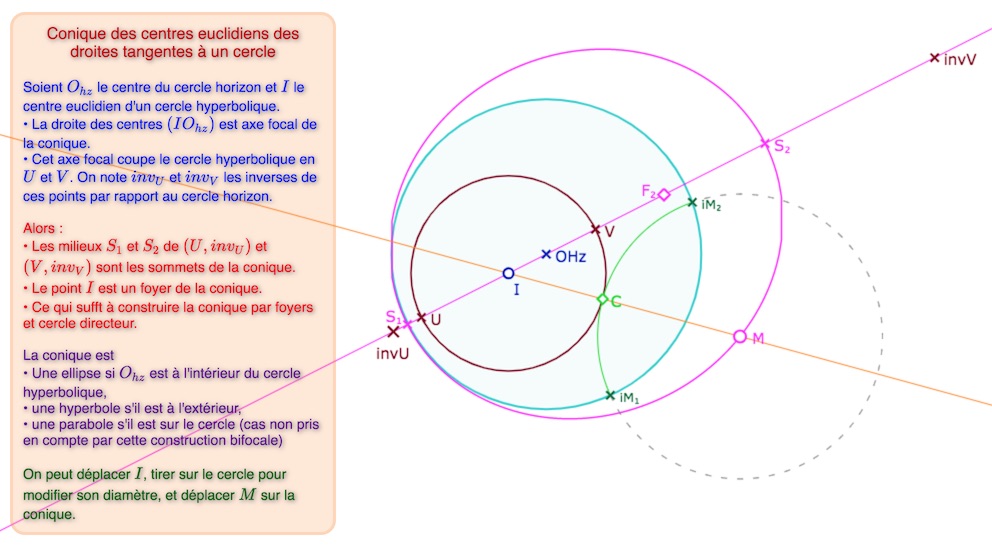
Ci-dessous, cas où la conique est une hyperbole avec M sur chaque branche.
Ouvrir cette figure dans un nouvel onglet
Retour sur la construction de l’image d’un pinceau par une demi-rotation
On commence par simplifier la construction de l’axe (éventuel) de l’image d’un pinceau par une demi-rotation.
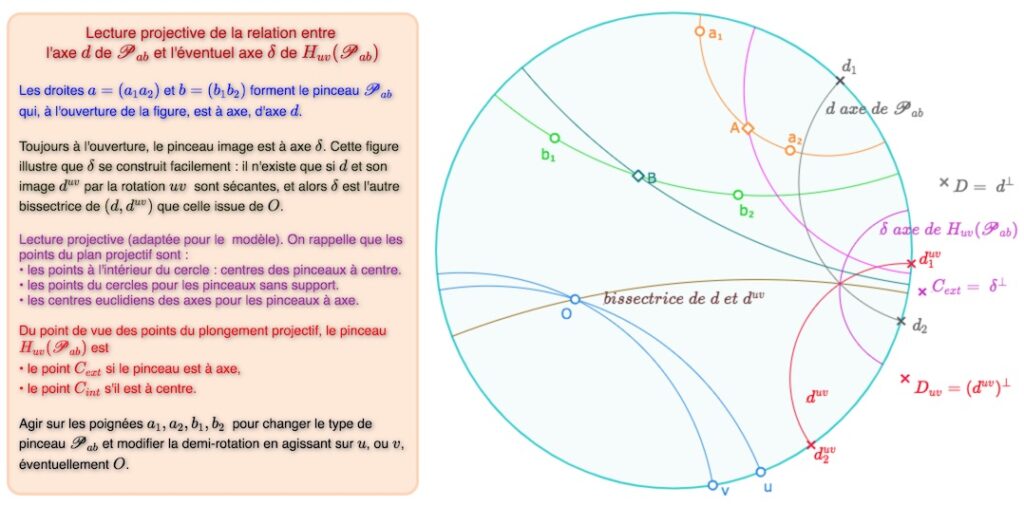
Dans cette figure, la bissectrice est construite comme la droite du pinceau \((d, d^{uv})\) passant par \(O\) ce qui fait qu’elle existe dans l’illustration ci-dessous à gauche. Le point nommé \(D_{uv}\) n’est pas l’image de \(D\) par \(uv\).
En bas à droite, on illustre le premier résultat mentionné dans la page précédente : l’image d’un pinceau à centre est à centre, ou encore, avec le vocabulaire de Bachmann pour le plongement : l’image d’un pinceau propre est un pinceau propre.
Ouvrir cette figure dans un nouvel onglet.
En pratique, c’est cette construction, adaptée pour pouvoir être transformée en macro, qui va être utilisée dans la suite des constructions. En particulier, les logiciels actuels de géométrie dynamique permettent de construire un unique point qui est, selon les circonstances, soit le point \(C_{int}\), soit le point \(C_{ext}\).
Caractérisation du type de pinceau image en rapport à \(C_{uv}\).
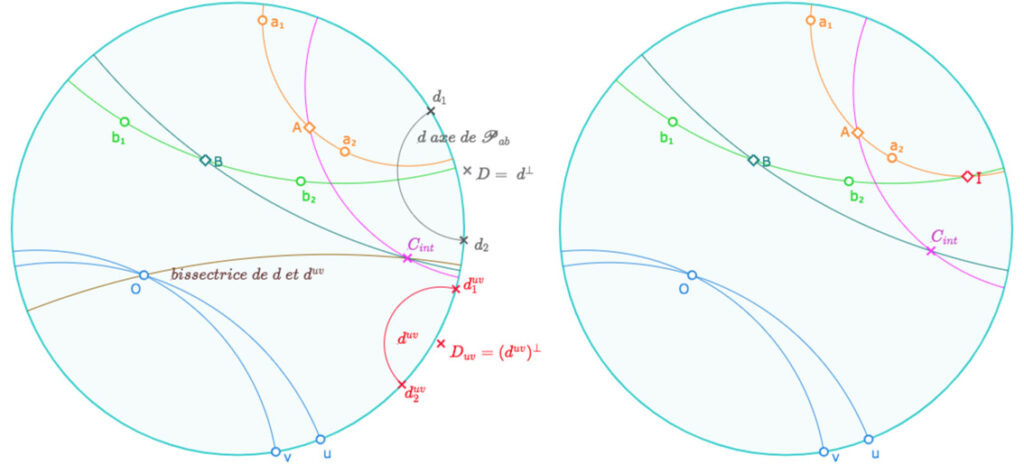
Reprenons la figure précédente, en ajoutant le cercle \(C_{uv}\). Dans l’illustration de gauche, l’image du pinceau par \(H_{uv}\) est à centre, de centre \(C_{int}\), intersection de la perpendiculaire commune à \(d\) et \(d^{uv}\) et de la droite du pinceau \(\mathscr{P}_{d \, d^{uv}}\) passant par \(O\), aussi axe de symétrie de \((d,d^{uv})\). A droite l’image est un pinceau à axe , de point idéal impropre \(C_{ext}\). La droite rose n’est plus la perpendiculaire commune à \(d\) et \(d^{uv}\) mais la perpendiculaire à la bissectrice (axe de symétrie) issue de \(O\).

Il est alors clair que le pinceau image devient sans support quand les points \(d_1\) et \(d_2^{uv}\) sont confondus. Or, à gauche les axes \(d\) et \(d^{uv}\) ne rencontrent pas le cercle \(C_{uv}\) alors qu’à droite, ils rencontrent le cercle. On peut alors, dans un premier temps, conjecturer qu’à la frontière, dans le cas d’un pinceau image sans support, ces deux axes sont tangents au cercle \(C_{uv}\).
Construction d’un pinceau à axe dont l’image est sans support
Le principe de la construction est résumé dans les commentaires de cette figure. On justifie aussi pourquoi, si \(d_1=d_2^{uv}\), l’axe \(d\) est tangent à \(C_{uv}\)
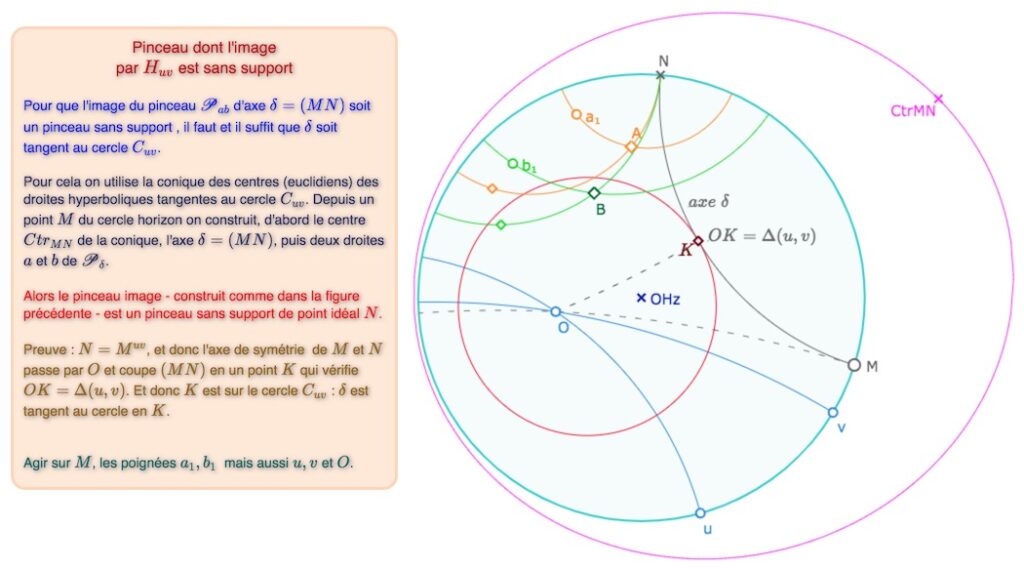
Lancer cette figure dans un nouvel onglet.
Cette propriété devient alors une propriété caractéristique du type de pinceau image d’un pinceau à axe. Il est :
• à centre, si \(d\) ne coupe pas \(C_{uv}\),
• à axe, si \(d\) coupe \(C_{uv}\),
• sans support, si \(d\) est tangent à \(C_{uv}\).
Les droites idéales propres
On aborde désormais les concepts proposés par Bachmann. Il commence par définir les droites idéales propres \(g(a)\) associées aux droites \(a\) du plan métrique comme indiqué sur l’illustration suivante. On notera que Bachmann défini ces droites idéales propres comme ensemble de points … alors que ce n’est pas le cas dans le cadre initial de son axiomatique.
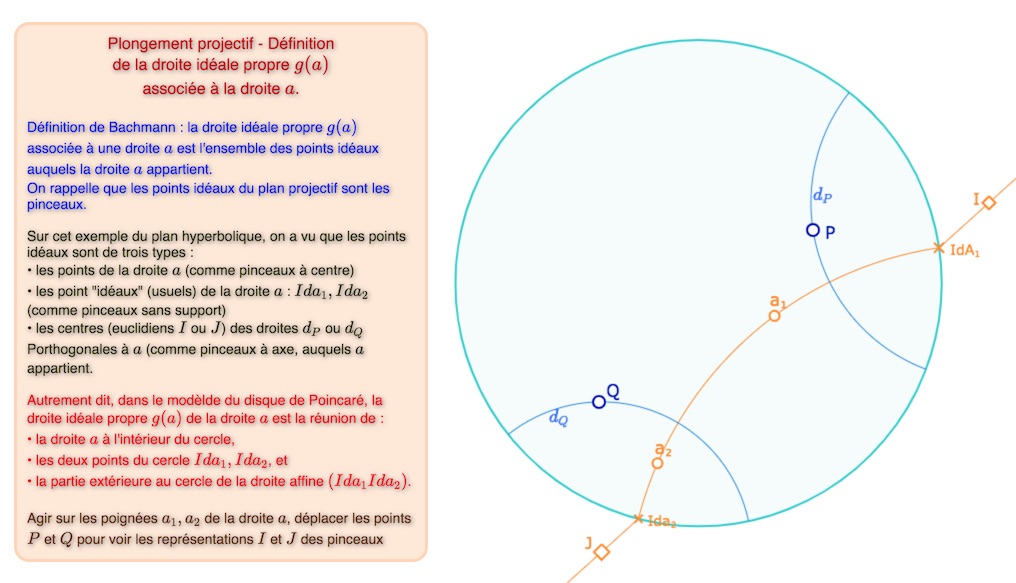
Ouvrir cette figure dans un nouvel onglet (pour voir le déplacements des points \(I\) et \(J\)).
Les demi-rotations conservent les droites idéales propres : \(H_{uv}(g(d)) = g(H_{uv}(d))\)
C’est bien entendu le principal résultat théorique. L’ensemble des illustrations de ce résultat tient dans cette figure qu’il est préférable de manipuler pour mieux s’approprier ce concept de droite idéale propre.

En effet à l’ouverture, les axes \(\alpha\) et \(\gamma\) existent, et les points idéaux associés \(H_{uv}(C)\) et \(H_{uv}(A)\) sont donc impropres, et ils sont bien sont bien sur \(g(H_{uv}(d))\) (sur les demi-droites).
Ensuite on agit sur le point \(C\) pour que \(\gamma\) disparaisse et que le pinceau \(H_{uv}(\mathscr{P}_c)\) devienne un pinceau à centre. Pour visualiser dynamiquement ce que devient \(H_{uv}(C)\) on peut afficher un pinceau effectif d’axe \(c\) avec les droites \(p\) et \(q\). Le point \(H_{uv}(C)\), centre du pinceau image, devient un point idéal propre comme on le voit dans cette illustration :

\(H_{uv}(C)\), centre du pinceau \(H_{uv}(\mathscr{P}_c)\), où le pinceau à axe \(\mathscr{P}_{c}\) est représenté par \(\mathscr{P}_{pq}\).
On vérifie que \(H_{uv}(C)\) est bien sur la partie propre de \(g(H_{uv}(d))\), soit \(H_{uv}(d)\).
Un bouton permet aussi de visualiser l’image du point \(B\) de \(d\). Ce point \(H_{uv}(B)\) est construit comme milieu de \([B\; B^{uv}]\) obtenu par médiatrice. Il est – évidemment – sur \(H_{uv}(d)\).
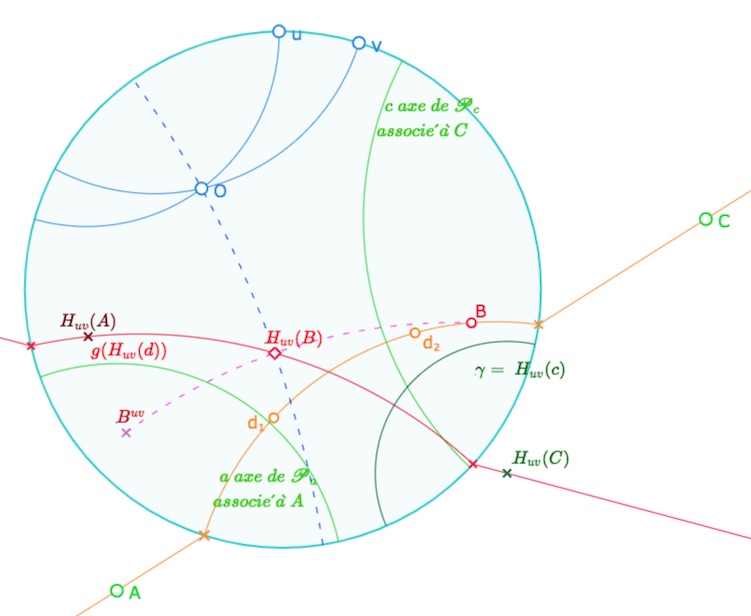
Sur cette figure, on a aussi déplacé \(A\) pour que \(H_{uv}(A)\) devienne un point idéal propre.
Ouvrir cette figure générique dans un nouvel onglet.
\(H_{uv}\) surjective sur l’ensemble des pinceaux
Même si ce résultat semble clair quand il est illustré et interprété dans un modèle aussi riche que le disque de Poincaré – en particulier disposant de la continuité – en réalité ce que l’on vient d’illustrer montre essentiellement la simple inclusion \(H_{uv}(g(d)) \subset g(H_{uv}(d))\). Pour avoir l’égalité, il faut s’assurer que \(H_{uv}\) est surjective sur l’ensemble des pinceaux, ce qui n’est pas une évidence en soi dans le cadre aussi général de cette axiomatique. Voir le Aufbau 6.2. xi p. 98 pour les deux éditions de 1959 et 1973 pour la démonstration.
Le disque de Poincaré comme œilleton conforme sur le plan projectif de Klein
Ces figures ont un côté un peu hallucinant, mais c’est didactiquement intéressant : ne pas simplement prolonger des segments par les droites, ajouter, par le choix de la conformité du modèle, une singularité sur la frontière, évite, en terme de représentation, de « glisser dans le plongement », et force à la réflexion. Le disque de Poincaré peut ainsi être perçu comme un œilleton circulaire ayant des propriétés optiques déformantes particulières, rendant la partie de ce plan comme un plan hyperbolique conforme. D’un autre point de vue – en particulier en regardant l’approche alternative de Daniel Perrin – on peut aussi penser que choisir ce modèle pour illustrer le plongement, en créant cette singularité, apporte de l’opacité – et une singulière complication – dans un domaine où tout est pourtant simple et tellement plus lisse.
Les droites idéales
Comme nous avons introduit les demi-rotations dans la page précédente, il est naturel d’appeler désormais droite idéale tout ensemble \(d\) de points idéaux pour lequel il existe une demi-rotation \(H_{uv}\) de centre \(O\), désormais fixé(1), telle que \(H_{uv}(d)\) soit une droite idéale propre.
Dans le cadre de nos illustrations avec le modèle du disque de Poincaré – compte tenu qu’il s’agit d’une « seconde axiomatisation » et que l’on connait le modèle projectif de Klein – il est clair qu’avec cette définition, les droites idéales sont, sauf cas particuliers, les droites projectives du plan, en pratique pour les constructions les droites affines.
(1) même si bien entendu, \(O\) est manipulable dans les figures dynamiques. Avec cette définition des droites propres, il s’agit de vérifier que, dans toutes les configurations, pour le point \(O\) donné, il existe toujours deux droites \(u\) et \(v\) qui font qu’une droite idéale \(d\) donnée va être transformée en droite idéale propre par \(H_{uv}\).
Premières explorations
On quitte un temps le déroulé général de Bachmann pour explorer dynamiquement le concept de droites idéales dans le modèle hyperbolique du disque de Poincaré. Dans cette première illustration, \(M\) est un point de la droite affine \(a=(a_1a_2)\). Comme point idéal (ici toujours impropre car la droite \(a\) ne rencontre pas le cercle horizon) il est associé à un pinceau à axe \(\mathscr{P}(M)\) dont l’image est l’axe \(H_{uv}(\mathscr{P}(M))\), associé au point idéal impropre \(H_{uv}(M)\).
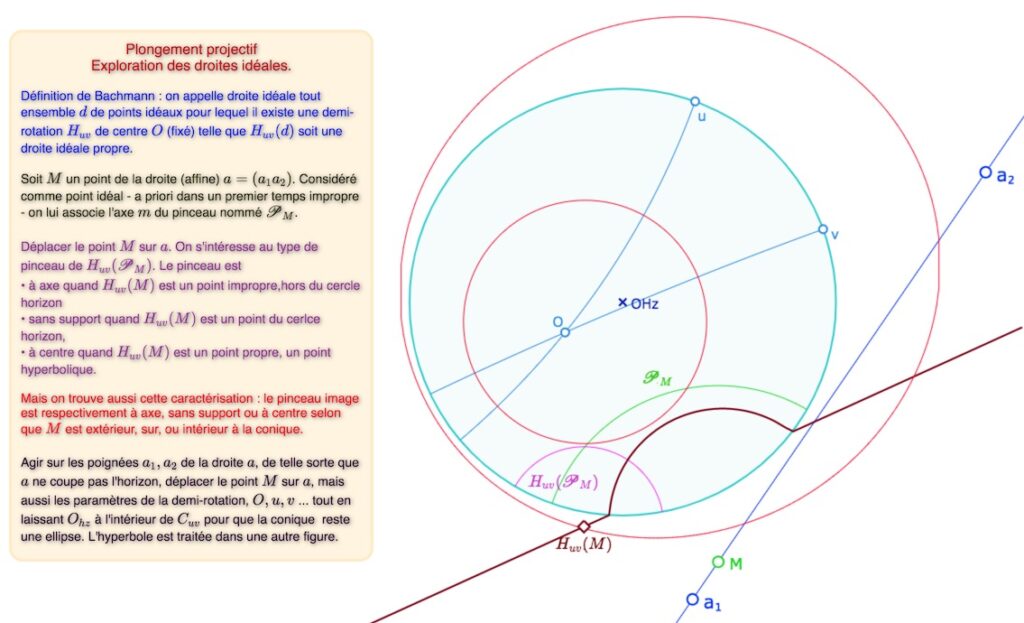
On a juste construit le lieu de \(H_{uv}(M)\) quand le point \(M\) décrit la droite \(a\). On vérifie (ou on constate selon …) déjà, que ce lieu est bien une droite idéale propre, puis les propriétés proposées dans la figure.
Lancer cette figure exploratoire dans un nouvel onglet. En particulier, dans cette figure, toujours conserver l’ellipse.
• Dans un premier temps ne pas couper le cercle horizon par \(a\),
• Puis couper le cercle horizon par \(a\) pour observer que la figure n’est pas (du tout) finalisée, en particulier \(H_{uv}(M)\) n’existe plus quand \(M\) devient un point hyperbolique (un point idéal propre) … qui n’est d’ailleurs pas bien placé. C’est ce que nous allons améliorer maintenant.
Dans la figure suivante, la droite idéale propre, image de la droite idéale, n’est plus un lieu mais elle est construite, la figure est donc plus fluide. Si la droite affine \(a\) coupe le cercle horizon, il est clair que la droite idéale passant par les points \(a_1\) et \(a_2\) n’est plus la droite affine, mais devient la droite idéale propre associée : c’est l’effet « œilleton déformant du modèle conforme » mentionné plus haut. On s’attend bien entendu (vu la section précédente) à ce que la demi-rotation sur cette droite idéale donne bien le point image attendu. Voyons cela en détail.
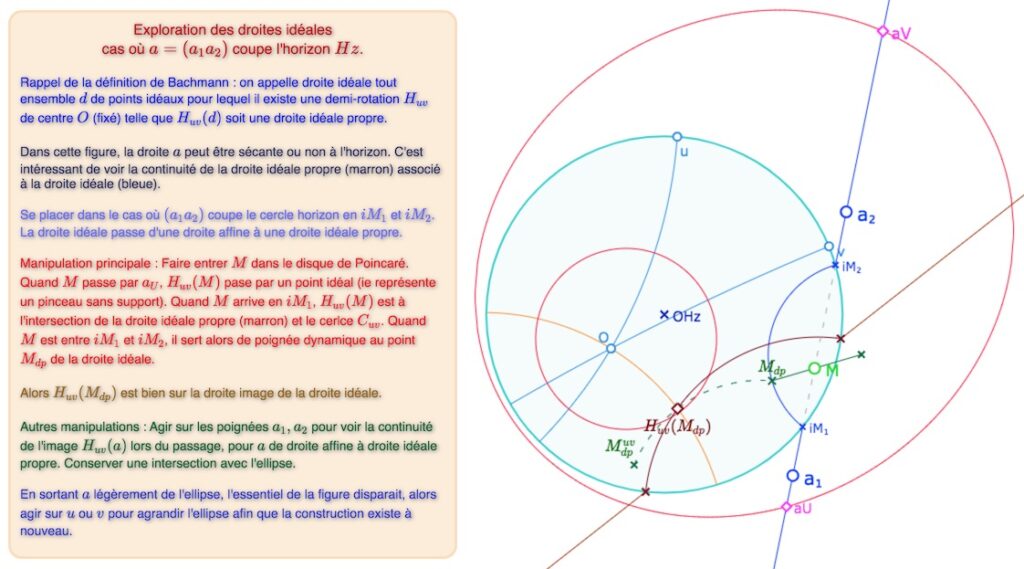
Ci-dessus le point \(H_{uv}(M_{dp})\) est construit comme le milieu de \(M_{dp}\) et \(M_{dp}^{uv}\), milieu obtenu par intersection du segment et de la médiatrice (orange).
Il est bien sur la partie « droite hyperbolique » de l’image générale \(H_{uv}(a)\).
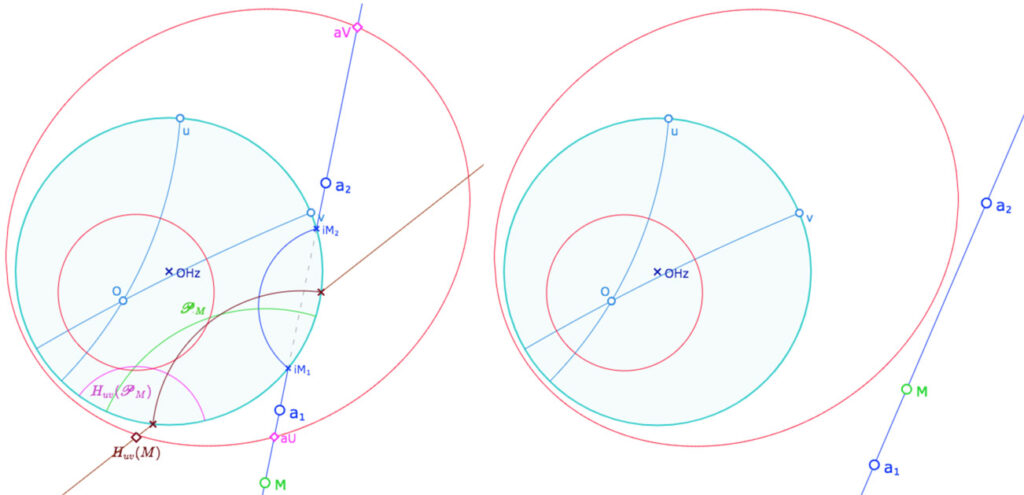
• à gauche, la situation à l’ouverture de la figure, la droite \(a\) coupe le cercle horizon, \(M\) est un point idéal impropre ainsi que \(H_{uv}(M)\).
• à droite, quand le droite \(a\) ne coupe plus l’ellipse toute la construction disparaît, il faut alors rapprocher légèrement les points \(u\) et \(v\) pour agrandir l’ellipse.
Ouvrir et manipuler cette figure dans un nouvel onglet. Là encore conserver la conique sous forme d’ellipse, le traitement de l’hyperbole sera abordé ultérieurement.
On notera une bonne robustesse de la figure quand l’arc de cercle de la droite idéale propre devient un segment passant par le centre du cercle (même s’il n’y passe pas « exactement » dans une manipulation à la souris, bien entendu).
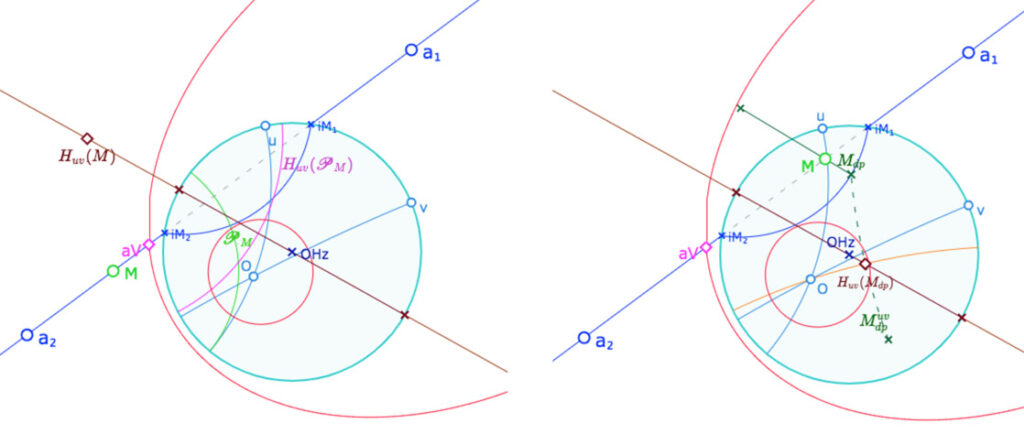
Dans certains cas, la figure peut fonctionner quand la conique est une hyperbole, mais il y a globalement un travail d’orientation à effectuer qui n’était pas nécessaire dans le cas borné de l’ellipse.
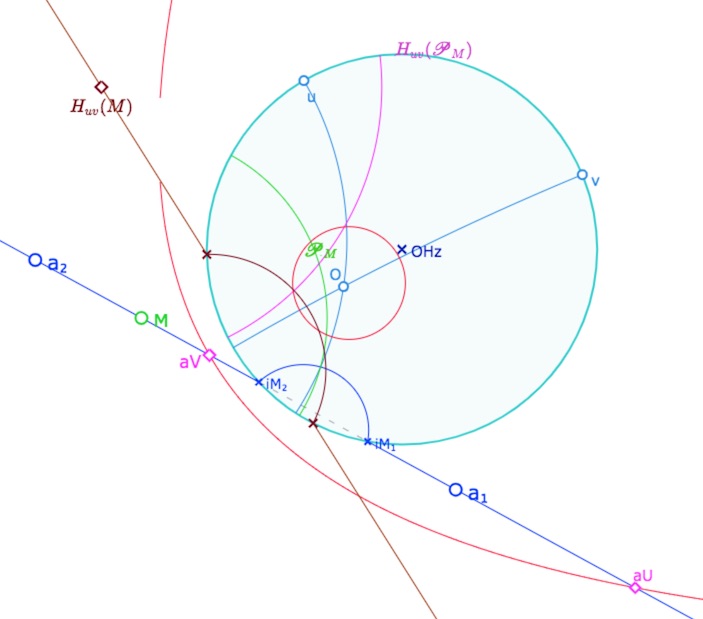
La conique des lieux des centres des droites tangentes à \(C_{uv}\) est ici une hyperbole (car \(O_{hz}\) est extérieur à \(C_{uv}\)).
La figure précédente est encore correcte dans cette configuration, en particulier car l’intersection de la droite \(a\) avec l’hyperbole est sur une même branche.
Cas d’une droite idéale tangente à l’horizon
Dans le plongement projectif de Bachmann, une droite idéale \(a\) peut être tangente à l’horizon. Alors, par définition même du cercle \(C_{uv}\), sa droite idéale propre \(g(a)\) est, elle, tangente à \(C_{uv}\).
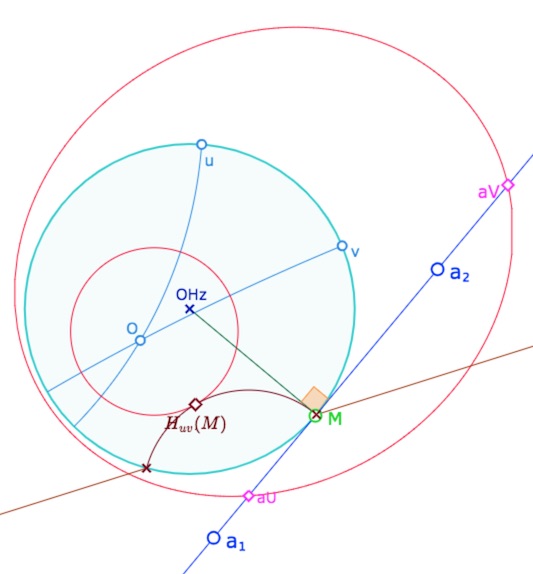
Quand \(M\) passe par le point de contact de \(a\) et de l’horizon, \(H_{uv}(M)\) est au point de contact de \(g(a)\) et de \(C_{uv}\).
Ouvrir cette figure dans un nouvel onglet.
C’est une grande différence avec l’approche de Daniel Perrin pour qui les tangentes au cercle unité (dans son vocabulaire – ce serait ici le cercle horizon), comme droites isotropes associées à la forme quadratique utilisée, ne sont pas des droites de son plongement, et donc l’axiome d’incidence n’est pas vérifié pour les points de ces droites, ce qu’il annonce d’ailleurs très vite :
Il nous semble, en effet, qu’il est préférable de renoncer à cet axiome dans un premier temps, même si le poids des traditions s’y oppose. Cette généralisation ne concerne d’ailleurs que le cas hyperbolique pour lequel elle revient à ajouter aux points du disque de Klein les points extérieurs. Dans ce cas, on verra que le surcroît d’efficacité obtenu en utilisant la polarité vaut bien quelques concessions.
Daniel Perrin – Partie 4 – pages 22-23 (liens dans l’article mentionné)
C’est une des raisons pour lesquelles son approche ne peut pas s’inscrire dans le cadre de l’axiomatique de Bachmann … et c’est aussi pour cela qu’elle est si intéressante.
Ajout d’une droite idéale spécifique
Nous reprenons l’exposé de Bachmann. En anticipant un peu la suite – en seconde lecture, sachant que Bachmann s’inspire de Hjelmslev – il va y avoir un point qui ne pourra pas avoir de polaire : c’est le point \(O\). Voyons cela, et comment Bachmann aborde cette question. Rappelons le résultat que nous avons nommé R1 dans la page précédente, mis en évidence précisément pour traiter cette situation :
R1 – Si un pinceau est à axe dont l’axe \(d\) passe par le point \(O\), alors son image est aussi un pinceau à axe, d’axe \(H_{uv}(d)\).
Il en résulte qu’il existe un ensemble de points qui ne peut avoir comme image par \(H_{uv}\) une droite idéale propre, et ceci pour aucun couple de droites \((u, v)\) sécantes en \(O\). C’est l’ensemble des pinceaux dont les points idéaux sont les pinceaux à axe dont l’axe passe par \(O\). En effet d’après R1, l’image par \(H_{uv}\) de ces points appartient au même ensemble : il est globalement invariant par \(H_{uv}\). D’où la définition suivante.
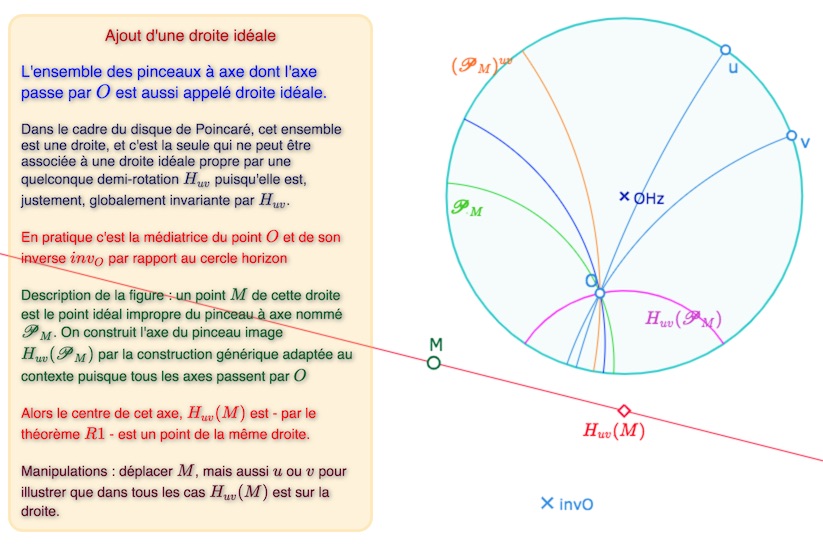
Ouvrir cette figure dans un nouvel onglet.
Bachmann appelle alors « polaire de \(\mathscr{P}_O\) » cette nouvelle droite idéale. C’est précisément pour cela qu’elle a été ajoutée.
La droite de l’infini du plongement projectif
Tout d’abord, dans notre illustration par le disque de Poincaré, les droites affines construites par le logiciel sont projectives au sens où elles ont un point à l’infini à cause du diamètre du cercle horizon qui appartient à chaque type de pinceau, à centre, à axe ou même sans support. Avec la question de la droite de l’infini c’est l’occasion de se pencher sur ces points.
Dans le cadre de notre illustration, la droite de l’infini est obtenue par l’image des diamètres du cercle horizon, considérés comme axe de pinceaux. Il suffit de reprendre la construction proposée en début de cette page de l’image d’un pinceau à axe par une demi-rotation, mais en refaisant la figure manuellement car aucune macro-construction ne peut fonctionner puisque les macros attendent deux arcs de cercle quand il y a un arc et un segment. On utilise alors les propriétés propres au modèle.
Exemple : soit à construire l’axe de symétrie d’un diamètre \((MN)\) et de son image \((M^{uv}N^{uv})\) quand les deux sont non sécants (cas où \(H_{uv}(M)\) est un point idéal propre, intérieur à l’horizon), il suffit de prendre la perpendiculaire commune à \((MN^{uv})\) et à \((NM^{uv})\) … et elle passe bien par \(O\). On trouve ainsi des propriétés simples pour toutes les situations, dont la perpendiculaire commune à \((MN)\) (segment) et \((M^{uv}N^{uv})\) (arc de cercle) qui est nécessaire pour construire \(H_{uv}(M)\) comme ci-dessous à gauche.

à gauche : la droite de l’infini est une droite extérieure au disque horizon. L’axe du pinceau image de l’axe \((MN)\) est la bissectrice extérieure de \((MN)\) et \((M^{uv}N^{uv})\) sécants en \(J\).
à droite, la droite de l’infini est une droite idéale propre. Dans cette configuration, \(H_{uv}(M)\) est l’intersection de la perpendiculaire commune à \((MN)\) et \((M^{uv}N^{uv})\) (verte) et de leurs bissectrice (marron).
Ouvrir cette figure dans un nouvel onglet
On remarquera que la droite de l’infini est une droite idéale propre ssi \(O_{Hz}\) est extérieur au cercle \(C_{uv}\), les points idéaux de la partie hyperbolique de cette droite étant obtenus à partir des tangentes à \(C_{uv}\) issues de \(O_{Hz}\) (illustration de gauche).
On notera aussi (cela reste à montrer, ce n’est qu’une conjecture ici) que, dans ce modèle, la droite de l’infini a comme direction la droite \((OO_{Hz})\).
Plan projectif d’incidence
Les droites idéales étant définies, Bachmann montre ensuite que la structure d’incidence réalisée est bien celle un plan projectif, à savoir que :
a) Par deux points idéaux distincts il passe une et une seule droite idéale
b) Deux droites distinctes ont toujours un et un seul point d’intersection
c) Il existe 4 points idéaux du plan dont trois quelconques ne sont jamais incidents à une même droite idéale.
Les demi-rotations sont des injections de l’ensemble des points idéaux dans lui-même. Mais plus précisément, il y a bijection entre l’ensemble des points du plan métrique et l’ensemble des points idéaux propres du plan projectif ainsi qu’entre l’ensemble des droites du plan métrique et l’ensemble des droites idéales propres : ainsi nous avons bien un plongement du plan métrique dans le plan projectif d’incidence.
Construction dynamique de droites idéales
Pour des constructions dynamiques, il convient de pouvoir construire une droite idéale passant par deux points, en particulier quand l’un est un point idéal impropre (extérieur au cercle) et l’autre un point idéal propre (intérieur au cercle). Contrairement à la même situation, avec une ellipse, dans le modèle non arguésien de Hilbert où il a fallu utiliser de la programmation, ici la construction se fait tout simplement en utilisant la puissance d’un point par rapport à un cercle et … la formule dite « de la médiane » :
\(MA^2-MB^2=2\overrightarrow{AB}.\overrightarrow{IM}\) où \(I\) est le milieu de \(A\) et \(B\).
Cela permet d’illustrer la version « plongement projectif » du théorème de Pappus, que Bachmann montre à nouveau (bien plus loin dans son ouvrage) dans ce nouveau plan projectif, avec l’utilisation de l’antiappariemment comme déjà abordé dans cette page.
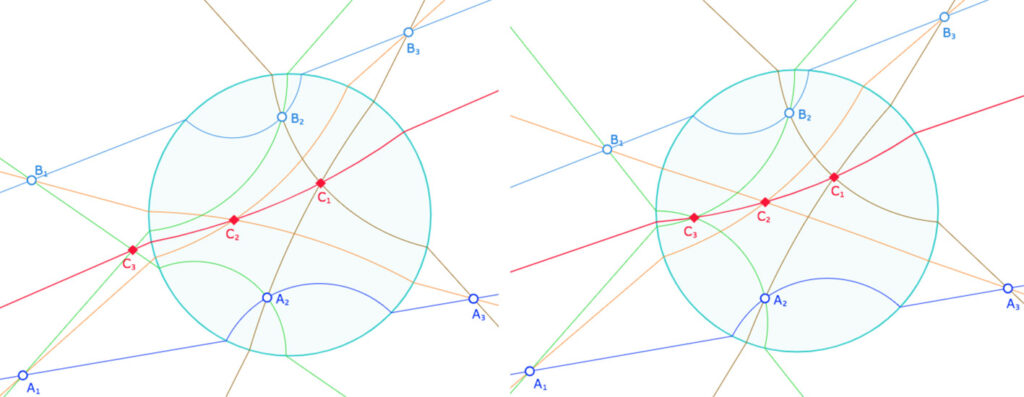
Dans cette illustration on a tracé la droite idéale \((C_1C_2)\). Elle passe par \(C_3\) que ce point idéal soit propre (à droite) ou impropre (à gauche).
En pratique \(C_3\) est un point unique (obtenu par programmation Javascript)

On peut alors ajouter une autre droite idéale, celle passant par \(C_{1ext}\) (caché sous le point \(C_1\)) et \(C_2\) pour permettre de faire sortir (voir les détails dans la figure) à la fois \(C_1\) et et même \(C_3\) du cercle horizon.
On n’est pas surpris de ces illustrations, c’est juste le Pappus projectif classique, regardé à travers l’œilleton « à déformation conforme » du disque de Poincaré. Ce qui est amusant, c’est de réaliser cette figure … depuis l’œilleton lui-même.
Ouvrir cette figure du plongement de Pappus dans un nouvel onglet.
Complément : le détail de la construction d’une droite idéale propre complètement dynamique est proposé dans la première section de cet article.
L’incidence étant acquise, il reste encore un gros morceau pour Bachmann, celui de l’instauration de la polarité. C’est l’objet de la troisième page sur ce plongement projectif.
Note technique : il manque un paragraphe – et surtout une figure – sur les droites idéales dans le cas où la conique des centres est une hyperbole. J’ai choisi de reprendre ce point, un peu plus technique, après la réalisation des figures sur la polarité.