On souhaite animer un polygone régulier, éventuellement étoilé tout en pouvant modifier la taille du cercle, et son centre.
Sans entrer dans le détail technique des réalisations, donnons quand même, pour une fois, quelques indications méthodologiques. On se donne un cercle de centre \(O\) passant par un point nommé \(taille\) dans les figures suivantes. On se donne ensuite un point \(M\) sur le cercle euclidien support du cercle elliptique. C’est ce point \(M\) qui sera animé – et en général caché dans les figures suivantes. Le recours au cercle euclidien support est nécessaire pour une animation, même si on peut croire qu’elle est faite sur les deux arcs de cercles. Ce point \(M\) – qui peut être hors plan elliptique est d’abord transformé en point elliptique (\(PtEll\) dans les figures, dont le nom est caché)
Le reste se fait simplement par symétrie orthogonale en commençant par le symétrique de \(PtEll\) par une droite d’angle avec la droite \((O PtEll)\), la moitié de l’angle au centre (45° pour un carré, 36° pour un pentagone). Voici l’exemple d’un carré.
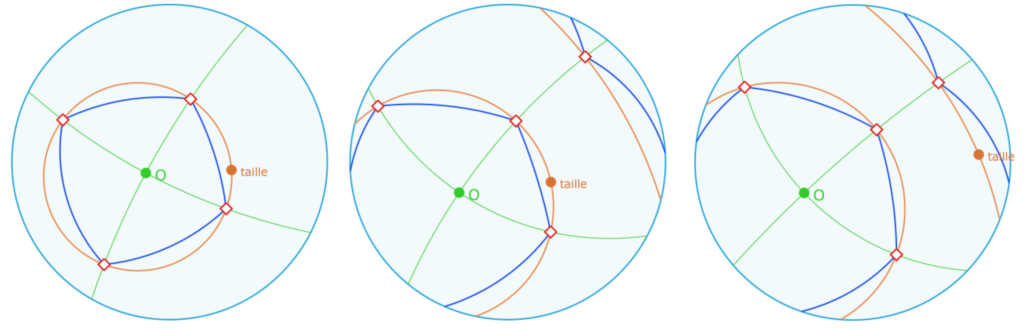
Déplacer les points \(O\) et \(taille\). Le carré n’est pas adapté au « retournement de l’animation », le tester plus loin
Pentagone étoilé
Dans la figure suivante, observer que la rotation elliptique du pentagone s’inverse quand l’orientation de l’arc contenant le point taille s’inverse comme les deux illustrations de droite. Réfléchir pourquoi, sachant que le point M sur le cercle support tourne toujours dans le même sens.
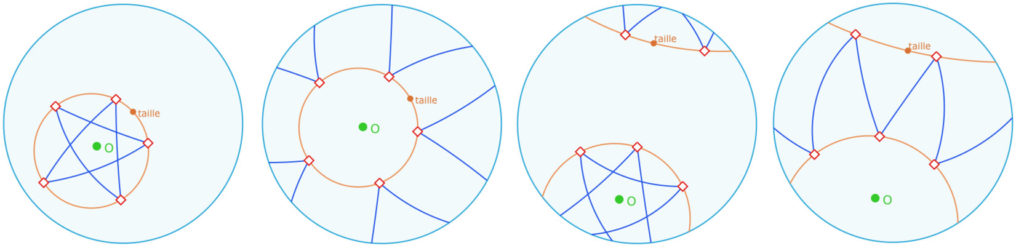
Exemple de ce que l’on peut obtenir avec la figure suivante en agissant sur les deux points accessibles de la figure.
Octogone étoilé P(8,3)
La même méthode permet de faire des constructions originales et sympathiques. On a choisi le polygone à 8 côtés car sa construction demande un nombre optimum de d’objets intermédiaires.
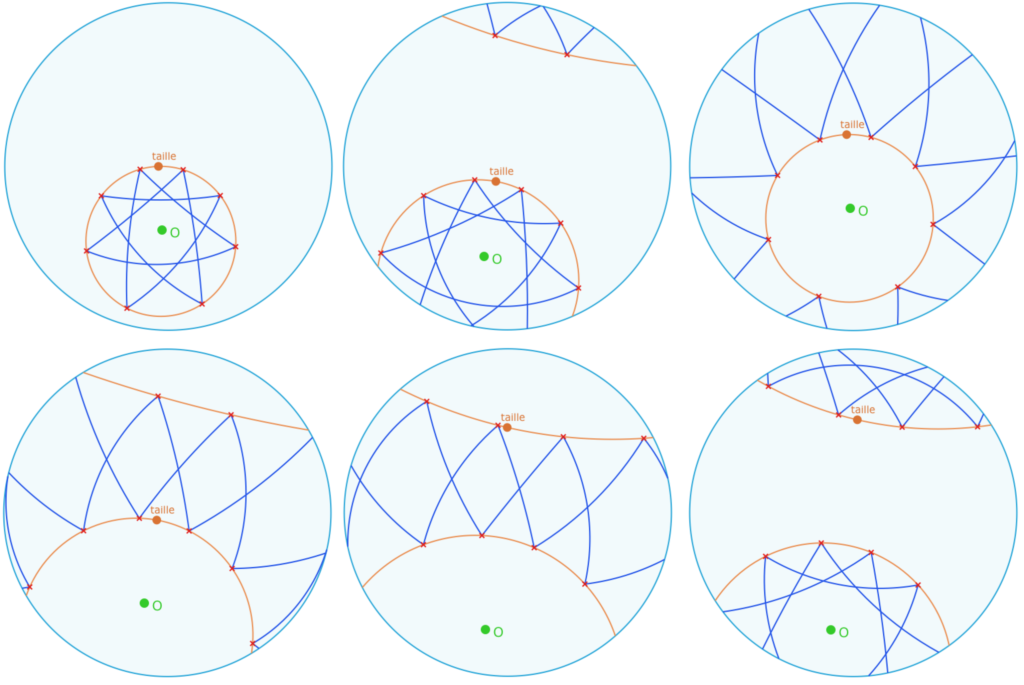
quelques illustrations des possibilités, avec inversion de la rotation dans les deux derniers cas
Trois polygones elliptiques en animation automatique, cela peut être parfois beaucoup sur une seule page. Il peut être nécessaire de relancer la page. D’autres polygones sont proposés dans les pages de blog, dont un avec deux curseurs.
On peut télécharger les trois figures de cette page