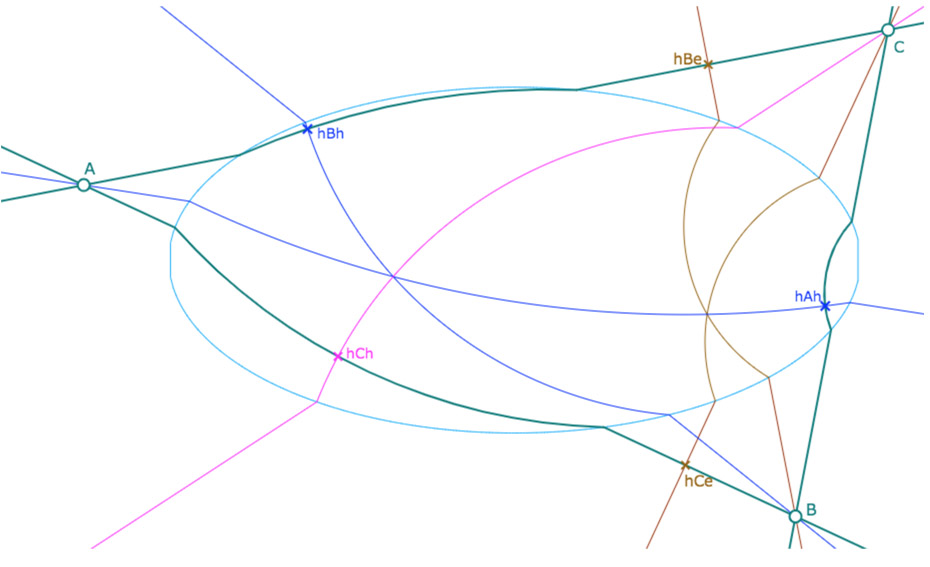
Les triangles dont les sommets sont extérieurs à l’ellipse peuvent avoir assez facilement six hauteurs, deux par sommets. Les possibilités de réalisation de triangles ayant un, puis deux orthocentres sont alors nombreuses en terme de mélange des hauteurs pour une intersection commune.

Les 12 intersections des hauteurs prises deux à deux, cas des trois sommets extérieurs.
D’autres situations existent quand un des sommets – au moins – est à l’intérieur de l’ellipse.
Cette page est simplement un premier contact avec ce thème, dans lequel on n’aborde que quelques cas particuliers. Même si c’est un projet à moyen terme, on est encore bien loin d’une approche exhaustive.
Un cas particulier : orthocentres hilbertien et euclidien séparés
L’exemple le plus simple de triangle bi-orthocentrique, est aussi peut-être le plus spécifique de la géométrie de Hilbert. En effet, puisque les triangles peuvent avoir 6 hauteurs, on peut, en plus de l’orthocentre euclidien classique (réalisé toutefois sous certaines conditions) avoir un orthocentre « purement hilbertien », c’est-à-dire avec trois hauteurs hilbertiennes. Ce cas est facile à réaliser car c’est le cas ordinaire des triangles orthocentriques.
Deux orthocentres « séparés » avec six hauteurs.
Préférer ouvrir cette figure dans un nouvel onglet
Précision pour toutes les figures de cette page : quand les hauteurs disparaissent à l’écran, elles sont simplement cachées. Il en résulte que les points d’intersection des hauteurs continuent à s’afficher même si les hauteurs n’existent plus. C’est un choix de type « figure de travail » … qui pourrait être amélioré.
Dans le modèle de Moulton, les triangles ne peuvent avoir que 5 hauteurs, et donc une telle construction est bien spécifique de la géométrie non arguésienne de Hilbert.
Principe de construction des figures suivantes
Mais les triangles bi-orthocentriques peuvent être, bien entendu, plus généraux. Pour détailler comment on peut en construire, et en particulier, utiliser la figure générique qui va être présentée, il peut être utile de préciser un peu la méthode de programmation.
Voici le programme, élémentaire, utilisé dans la figure précédente. On peut même être surpris de son efficacité pour trouver des triangles orthocentriques. C’est simplement une recherche dichotomique construite sur l’ordonnée des deux points d’intersection des hauteurs prises deux à deux..
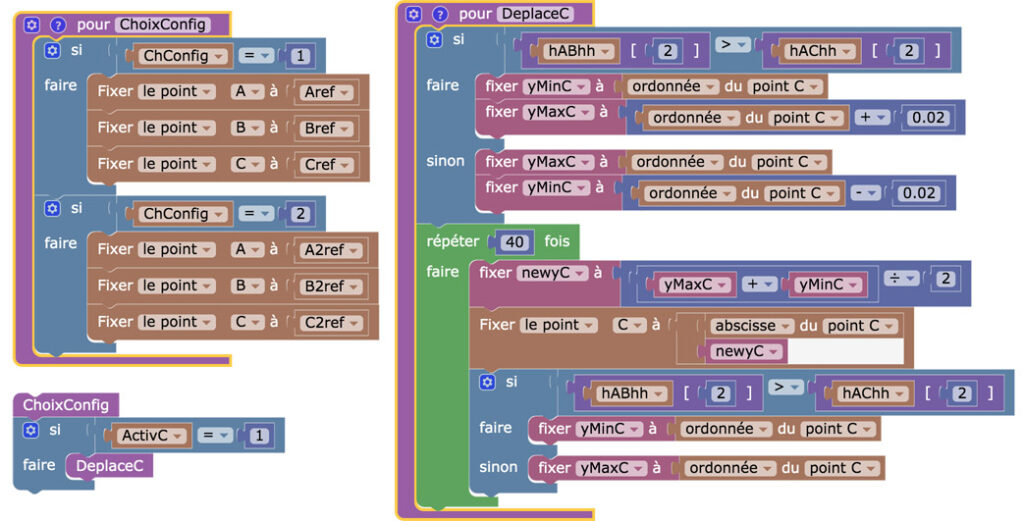
Rappel : dans DGPad (JavaScript) l’abscisse est la coordonnée d’indice 0 et
l’ordonnée d‘indice 1, dans Blockly les indices sont respectivement 1 et 2.
Ce que l’on va devoir étendre pour la recherche des double orthocentres est :
• le choix des intersections : on aura deux couples de termes au lieu d’un seul.
• le choix de l’abscisse ou de l’ordonnée du point (variation horizontale ou verticale)
• l’amplitude de la variation : on ira jusqu’à \(10^{-8}\) de l’unité, parfois même, dans les cas délicats jusqu’à \(10^{-9}\) soit moins d’un millionième de pixel.
• le sens de l’inégalité dans la première ligne du programme.
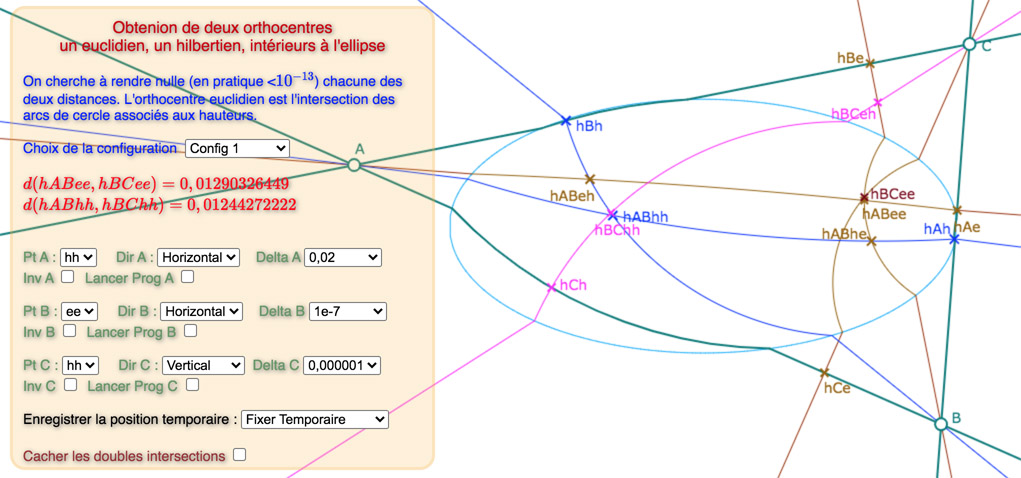
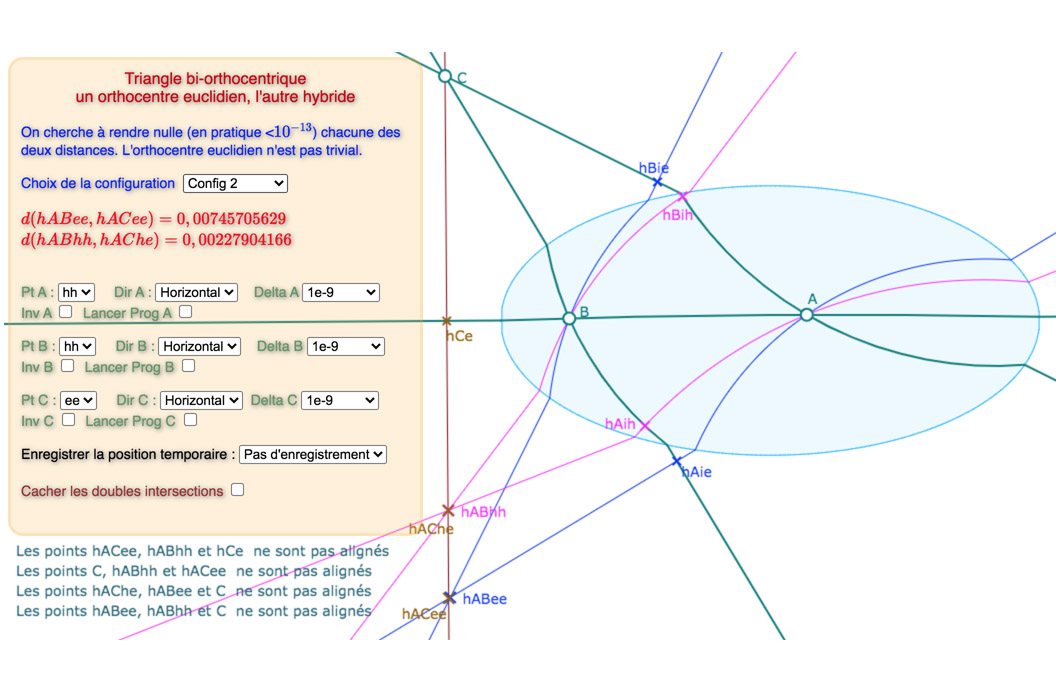
On a choisi de faire la recherche manuellement, pour voir les étapes – et aussi parce que c’est plus immédiat à réaliser … ce qui transforme la figure en « petit tableau de bord ». Voici une étape de la recherche, proche de la solution.
Le tableau de bord de la figure
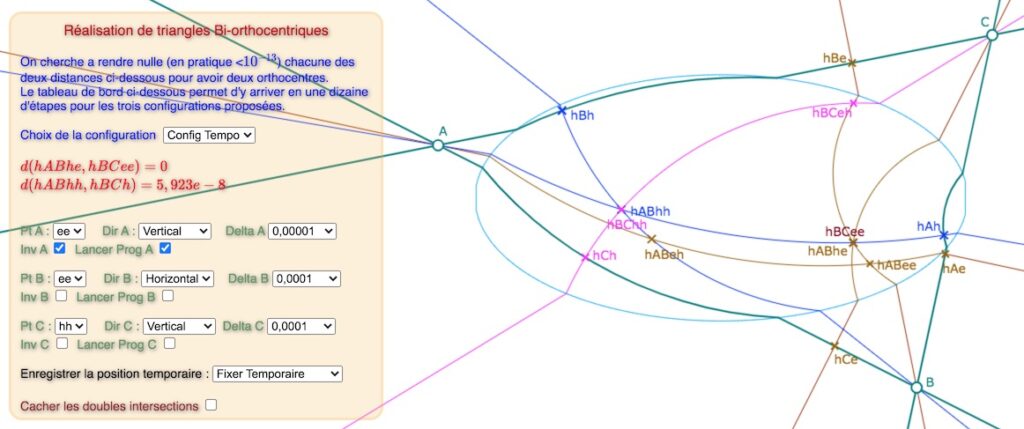
Le pop-up ee/hh permet de passer de l’orthocentre en \(h_{BCee}, h_{ABhe}\) à celui en \(h_{BChh}, h_{ABhh}\). En effet, à chaque étape, on alterne entre un orthocentre réalisé (au sens de la distance nulle) en une intersection et l’approximation sur l’autre, avec une amélioration de précision d’un facteur parfois de l’ordre de 10 d’une étape à l’autre (détaillé plus loin).
Le pop-up Horizontal/Vertical permet de choisir une variation en abscisse ou en ordonnée
Delta : l’amplitude maximale de la dichotomie. L’unité étant de l’ordre de 600 pixels, une précision à \(10^{-3}\) (au départ) est de l’ordre du pixel, largement insuffisante. Toutefois, en quelques étapes, rapidement la figure ne bouge plus car la variation va aller du centième au cent-millième de pixel.
Inv : correspond à l’inversion de l’inégalité de départ. Cela revient à inverser – autour du point de référence, l’orientation de l’intervalle d’amplitude Delta, dans la direction choisie par le pop-up précédent : avec Inv et le pop-up H/V, on a parcourt 4 intervalles d’amplitude Delta centré autour d’une des intersections dans 4 directions.
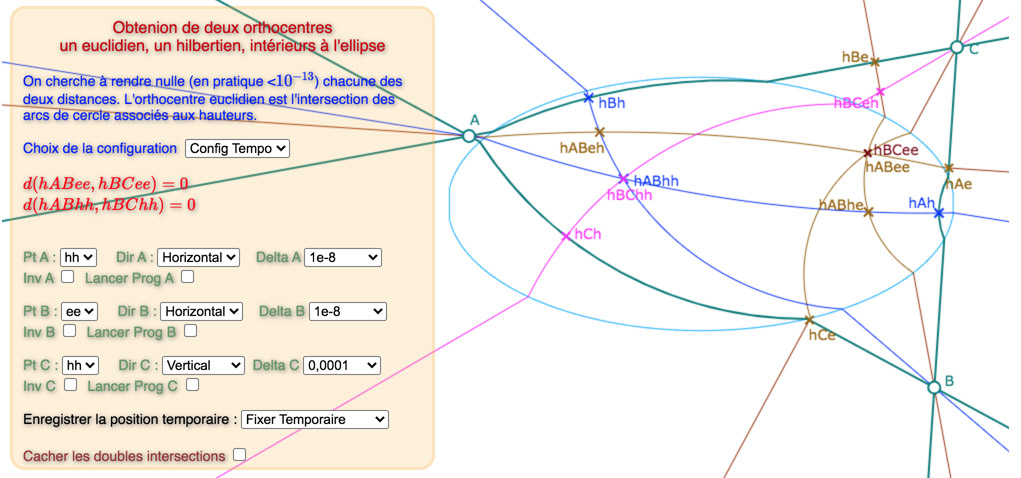
Le pop-up d’enregistrement temporaire : c’est la commande essentielle de ce tableau de bord. Elle mérite attention. Quand on cherche un triangle bi-orthocentrique avec cette figure, on teste diverses options, et il faut revenir en arrière si l’option ne convient pas. Autrement dit, à chaque progrès, on enregistre la configuration en cours par « Fixer Temporaire ». On passe (la première fois, sinon on y reste) à l’option « Config Tempo ».
Deux points importants sur le fonctionnement de cette figure :
• Comme le logiciel fonctionne en temps réel, il faut enlever l’option « Fixer Temporaire » et revenir à « Pas d’enregistrement » avant même de tester des nouveaux choix pour l’étape suivante, sinon le résultat est instantanément enregistré dans la configuration temporaire. C’est très simple à utiliser il faut juste être vigilant.
• L’alternative serait le choix \(Libre\) mais qui lui ne se souvient pas de l’étape précédente. En effet, il ne faut de toute façon pas laisser le pop-up sur une configuration (1 à 3) sinon, la boucle d’évènement relance cette configuration dans son état initial au prochain clic dans le tableau de bord de la figure.
• Par contre l’option \(Libre\) peut être utilisée pour tester d’autres configurations que celles proposées : choisir une configuration, l’enregistrer par « Fixer Temporaire » et aller sur « Config Tempo ».
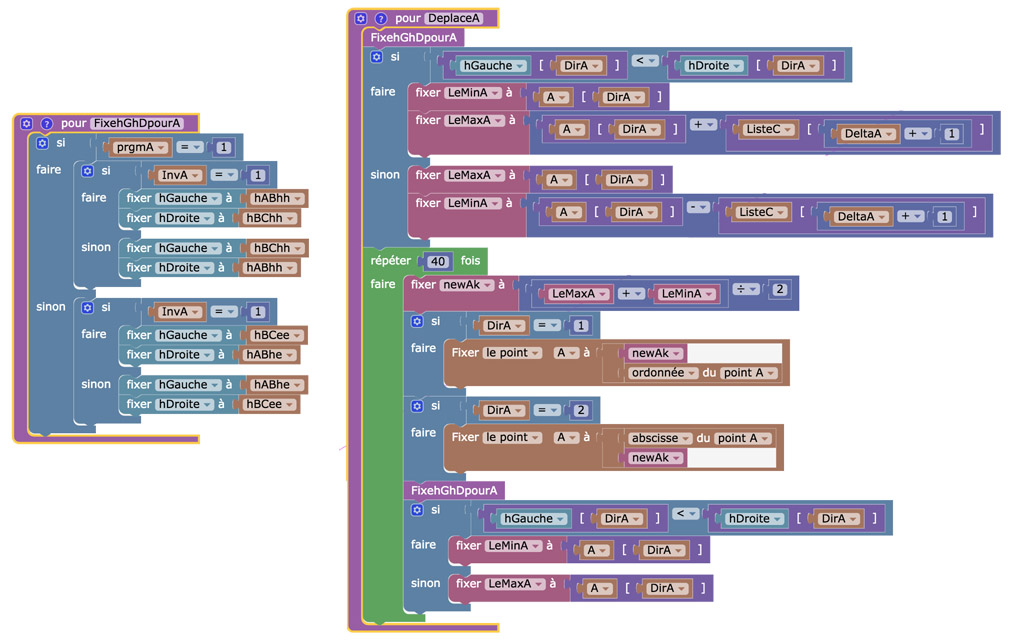
La modification du programme
Intérêt et limite de ce choix de résolution
L’intérêt est probablement dans le plaisir de chercher soi-même un chemin vers une solution et les différentes options qui se présente à nous. Mais l’inconvénient de cette approche par étape est son caractère statique : on cherche un triangle bi-orthocentrique, et non pas une situation modifiable à la souris (par les sommets) comme dans la figure ci-dessus ou celles des pages précédentes : on ne fait plus de géométrie dynamique … mais de la géométrie « statique ». Pour revenir à une situation plus dynamique, il faudrait, au minimum, réaliser un programme plus global qui ferait la recherche lui-même. Ce n’est pas difficile, car il n’y a pas beaucoup d’options, on pourrait probablement pouvoir déplacer les sommets en maintenant une situation bi-orthocentrique. Ce n’est pas d’actualité pour le moment, car il faut déjà faire un premier bilan exhaustif – d’un point de vue structurel – de la situation, mais cela pourrait être l’occasion d’une futur mise à jour.
Réalisation de premiers triangles bi-orthocentriques hybrides
Voici les trois premiers triangles proposés à la réalisation par le lecteur
Commencer par ouvrir la figure de travail dans un nouvel onglet
Cela permet – si on le souhaite – de suivre les différentes étapes de chaque configuration proposée ci-dessous, ou explorer soi-même les trois configurations préparées pour des solutions rapidement abordables.
Rappel : il faut enregistrer la configuration temporaire à chaque fois que l’on estime avoir fait un pas vers une solution. Et enlever l’enregistrement temporaire avant de commencer à cliquer sur un autre programme.
Les choix retenus
Voici les étapes proposées pour chacune des configurations. Le choix retenu est celui de privilégier l’alternance de situations orthocentriques : on passe d’un orthocentre d’un type « \(ee\) » ou « \(he\) » à l’autre. C’est un choix qui n’est pas indispensable. En ne le suivant pas, on peut – peut-être – trouver une solution plus rapidement. Au moins ce choix montre-t-il qu’il y a naturellement beaucoup de situations orthocentriques sur des intervalles très petits : ces étapes montrent qu’on en trouve plusieurs sur une variation inférieure au millième de pixel.
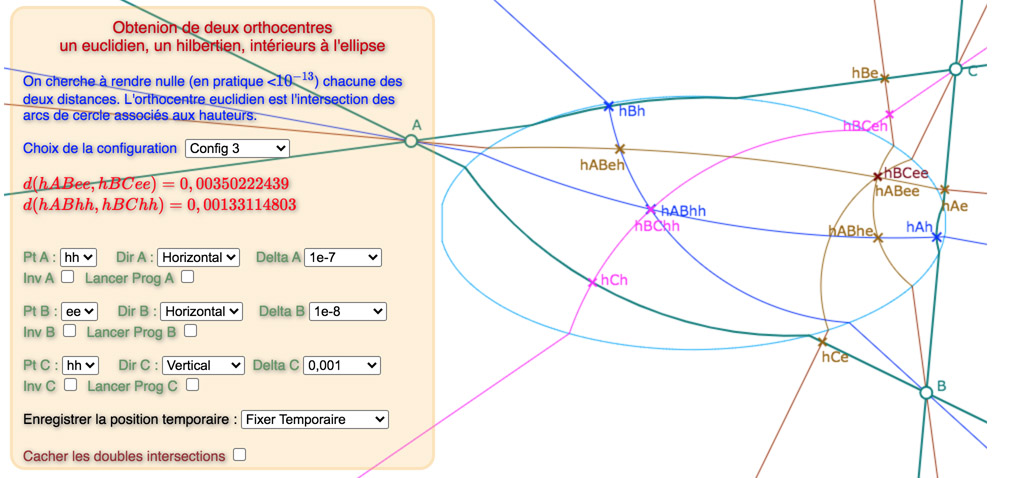
Configuration 1
Les 11 étapes proposées
Sur certaines étapes, on peut voir (par le pop-up ee/hh par exemple) que plusieurs essais ont été effectués avant le choix retenu … essais qu’il n’est pas utile de reproduire, bien entendu.
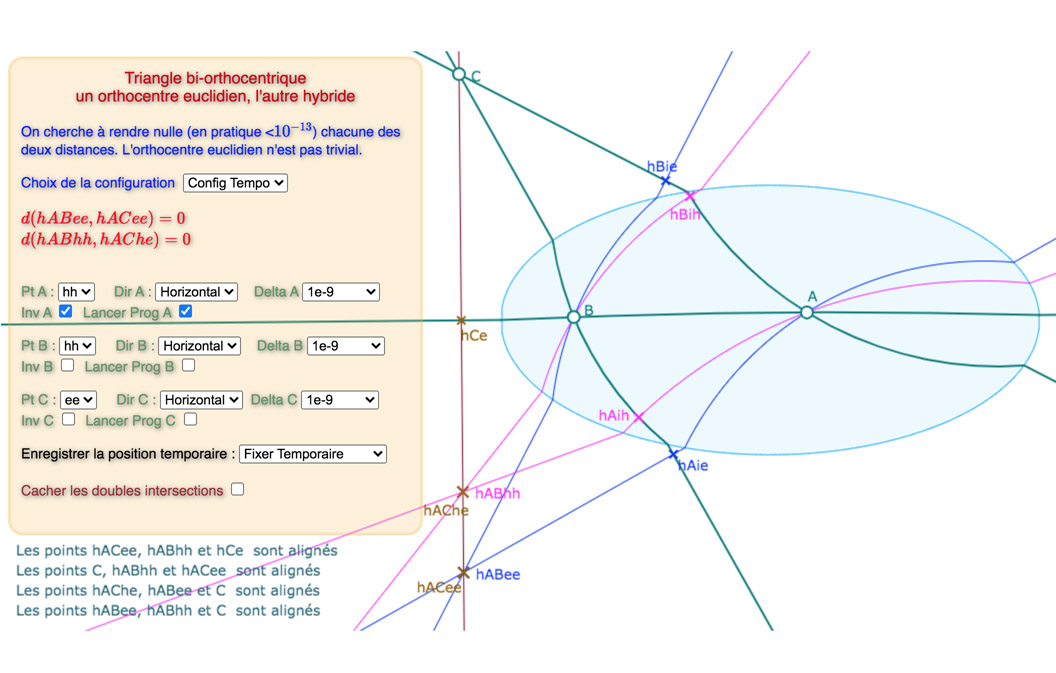
Configuration 2
Même remarque que ci-dessus. Par exemple pour passer de l’étape 2 à l’étape 3, il suffit de modifier \(ee/hh\) sur le point \(C\) et son Delta avant de lancer le programme en \(C\), le reste est inutile …
Treize étapes, c’est probablement un peu trop, on devrait pouvoir faire mieux …
Les 13 étapes proposées
Configuration 3
Là aussi, on imagine bien qu’on devrait pouvoir trouver un chemin plus court que celui proposé ici, en 12 étapes.
Les 12 étapes proposées
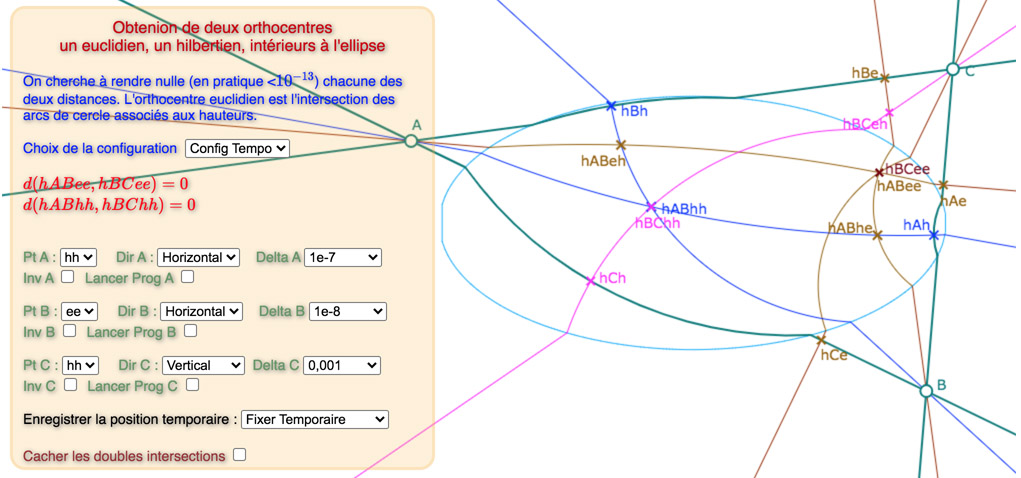
Retour sur deux orthocentres « séparés », un hilbertien et un euclidien mais ici intérieurs à l’ellipse
On reprend le même principe, avec une nouvelle figure car les intersections des hauteurs ne sont pas les mêmes : c’est là que l’on voit qu’une structure plus paramétrée, mais aussi avec plus de cases dans le « tableau de bord » aurait permis de travailler avec une seule figure … c’est en projet car paradoxalement, le code serait plus compact et plus efficace.
Dans les illustrations ci-dessous, on notera plusieurs intersections de hauteurs non utilisées dans la figure suivante, comme \(h_{ABeh}, h_{ABhe}\) ou encore \(h_{BCeh}\), ce qui illustre la potentialité d’autres orthocentres.
Trois nouvelles configurations en mode « 1. Départ 2. Solution avec points, et 3. Solution sans points »
Ouvrir la figure associée à ces trois configurations (s’ouvre dans un nouvel onglet)
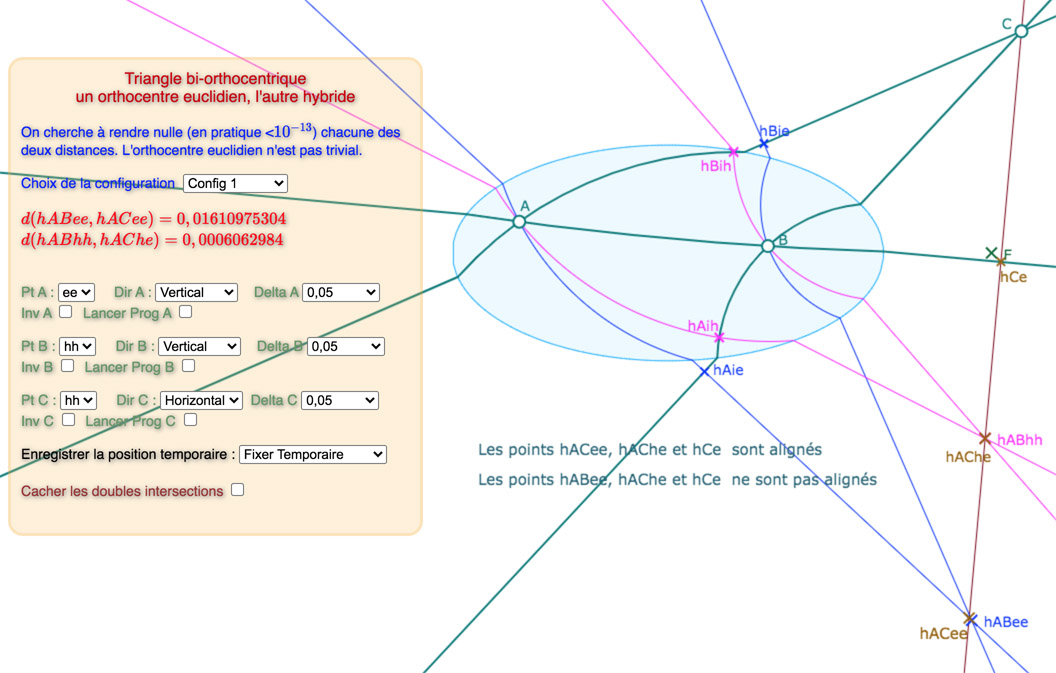
Voici des chemins possibles vers des solutions – mais on peut explorer d’autres pistes.
Configuration 1
• En dehors de la configuration de départ, on se place toujours dans la « Config Tempo » sinon on revient toujours sur la configuration de départ.
• Par ailleurs, la seule information utile est sur la ligne du programme activé … les autres correspondent à des essais.
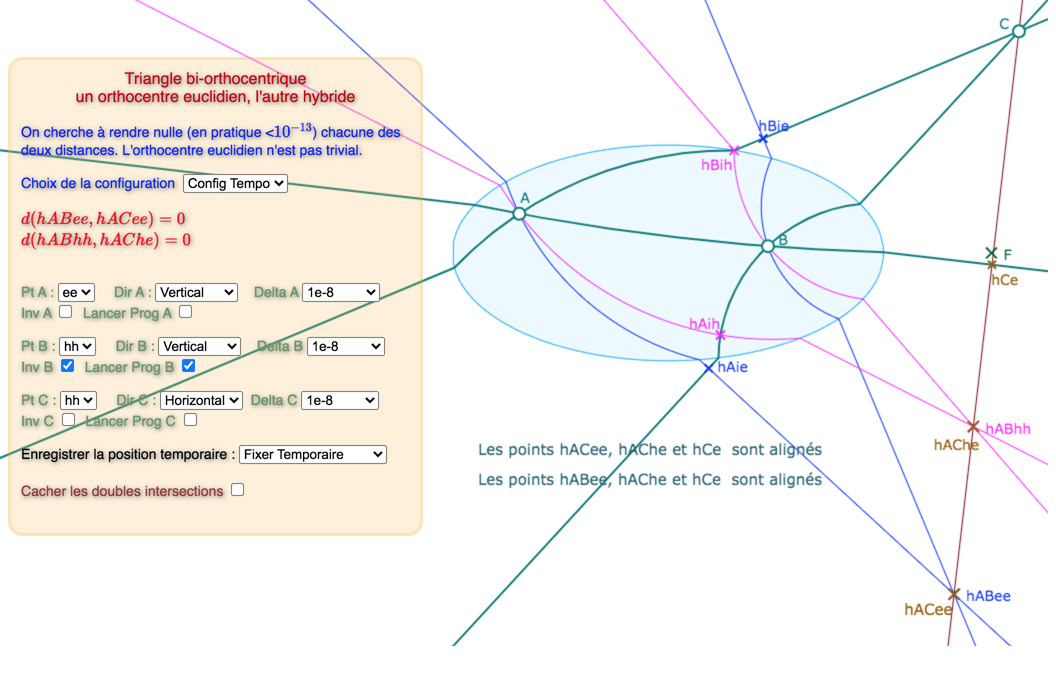
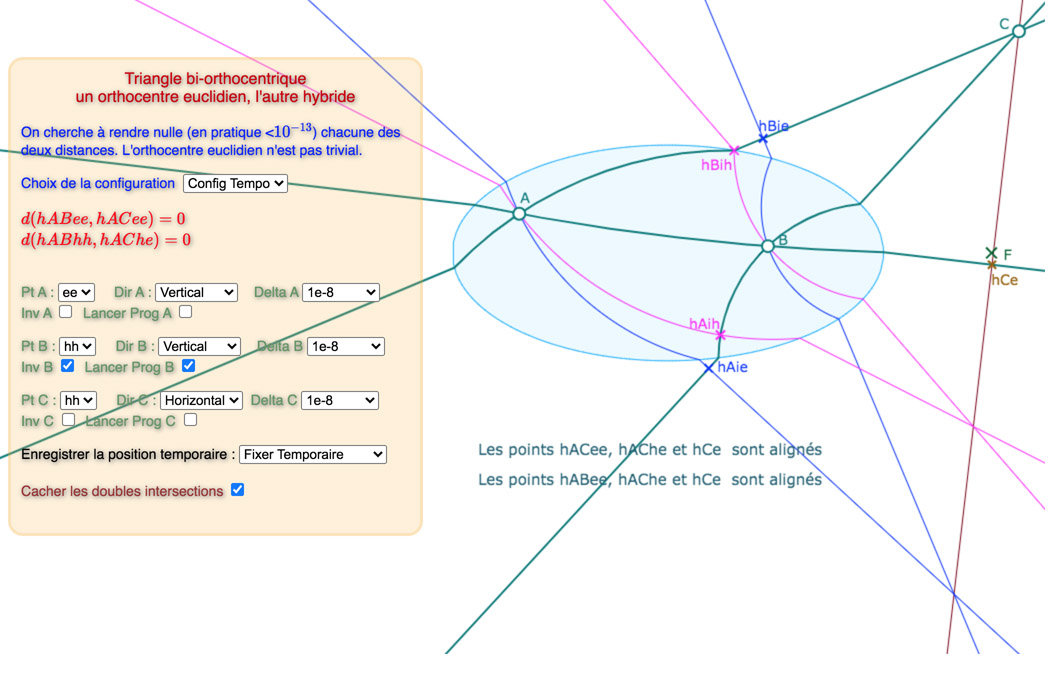
Chemin possible pour la Configuration 1
Configuration 2
Lire l’information ci-dessous à propos de l’étape 2
De manière très surprenante, dans l’étape 2, il faut agir sur le dernier pop-up et activer « Fixer temporaire » pour finaliser l’étape. J’ai bien entendu passer du temps sur cette question, repris en détail le programme – qui fonctionne comme on s’y attend dans tous les autres cas.
Il semble que ce soit une question numérique ou de mémoire. Un peu comme si le programme bloquait, en tout cas n’aboutissait pas en terme d’affichage, et se finalisait par une action dans la figure.
Rappel : on a volontairement fait des copies d’écran avant de fixer la configuration, mais bien entendu, il faut, à chaque étape – si on cherche par soi-même en particulier – activer l’item « Fixer Temporaire ».
Configuration 3
Les 9 étapes proposées
Pour terminer sur cette figure, voici une illustration, d’une propriété certes évidente, mais sympathique à illustrer :
Les deux droites des centres des arcs de cercles passant par les deux orthocentres sont sécantes en le centre euclidien de l’arc de cercle de la droite hilbertienne passant par les deux orthocentres.

La droite de Hilbert rouge passant par les deux orthocentres a
son arc centré sur l’intersection des deux droites des centres des deux orthocentres.
Exemple de triangles bi-orthocentriques
ayant deux sommets à l’intérieur de l’ellipse
On termine cette première approche des triangles bi-orthocentriques avec des cas de triangles ayant des sommets à l’intérieur de l’ellipse. Il y a moins de possibilités de hauteurs, mais avec des sommets intérieurs on peut trouver des situations où chaque sommet peut avoir deux hauteurs, et avec une cinquième hauteurs issue du troisième sommet, on peut chercher une bi-orthocentricité. Elle est moins simple à obtenir pour les raisons que l’on va voir avec les figures.
Voici les deux configurations que l’on propose de finaliser
Comme ci-dessus,. voici deux configurations en mode « 1. Départ 2. Solution avec points, et 3. Solution sans points ».
Ouvrir la figure associée à ces deux configurations (nouvel onglet)
Fonctionnement de cette figure
On peut commencer à utiliser cette figure en mode \(Libre\) pour sentir la sensibilité de cette question de bi-orthocentricité : obtenir un orthocentre est très facile, pour les deux, ce n’est pas évident.
On notera qu’il faut être vigilant à maintenir les hauteurs : dans les deux configurations, la hauteur hilbertienne issue de \(B\) est proche « de la sortie » de l’ellipse, et donc de disparaître.
La seconde configuration montre les limites de notre démarche, un peu comme si nos choix aboutissaient à une sorte de « convergence lente » vers une solution. Il y a aussi souvent plusieurs choix intermédiaires possibles … qu’il serait intéressant de traiter algorithmiquement. pour une meilleure optimisation des parcours.
Configuration 1
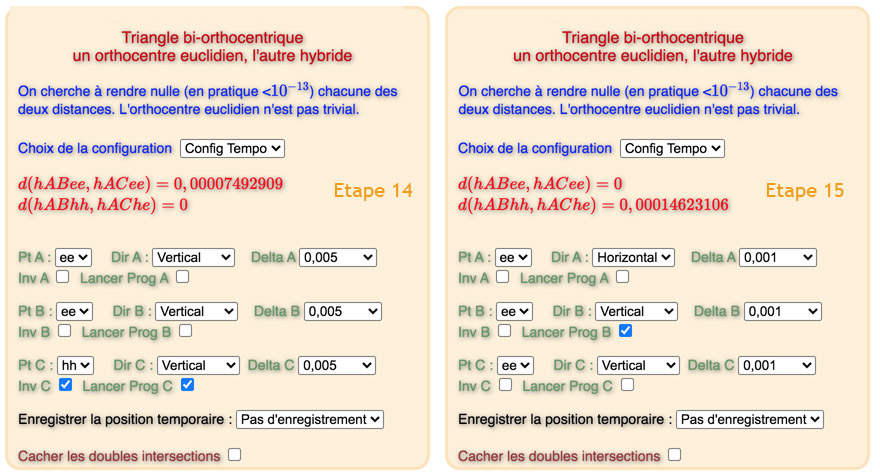
Les deux orthocentres de la configuration 1 en 15 étapes
La configuration reste assez classique. On peut choisir des variantes, mais il faut être prudent, car dans les premières étapes, on peut facilement faire disparaître une hauteur selon les choix autour des points \(A\) et \(B\).
La fin peut nécessiter des modifications, d’ajouter une ou deux étapes, cela dépend de peu de choses, en particulier si on ne fixe pas l’étape par « Fixer temporaire ». Il peut parfois (en fin de parcours) être nécessaire d’activer le programme deux fois de suite dans la même configuration pour « finaliser » une étape.
Configuration 2
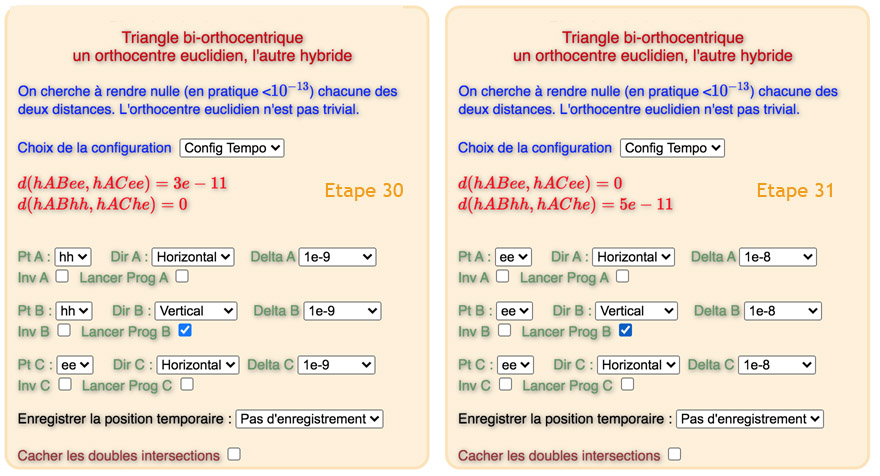
Cette configuration a été retenue pour sa lenteur de convergence vers une solution, en particulier à partir des étapes 20. On peut chercher d’autres pistes que celles proposées. Cela montre aussi – une nouvelle fois – qu’il y a de très nombreux orthocentres (simples) pour des variations infinitésimales des sommets (on rappelle qu’une variation de \(10^{-9}\) correspond à moins d’un millionième de pixel). Voir plus loin, l’option « Config2 E30 ».
Un chemin de 34 étapes pour résoudre cette configuration. Remarquer les deux étapes 34 proposées.
Voici la figure en mode 34b (la 34a est dans la présentation des deux configurations)

En pratique dès l’étape 28, deux des quatre tests d’alignement peuvent être confirmés.
Ici – 34b – les 4 alignements cherchés ne sont pas concluants. Ils le sont en 34a.
Une configuration adaptée : Config 2 E30
En fait dans cette figure, vous avez la possibilité de choisir de prendre la configuration 2 à l’étape 30 pour aller plus vite vers une solution. Attention, les réglages sont par défaut celles de départ, il faut aller vers des amplitudes \(Delta\) de l’ordre de \(10^{-8}\)
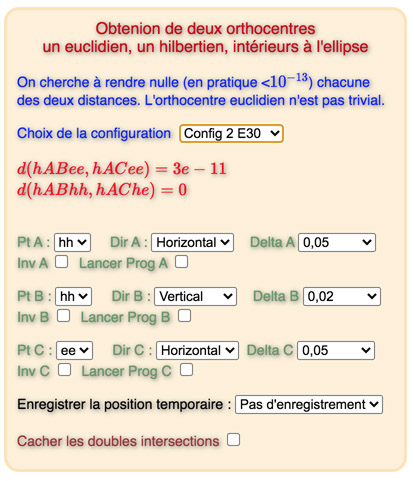
Triangles orthocentriques ayant deux hauteurs parallèles
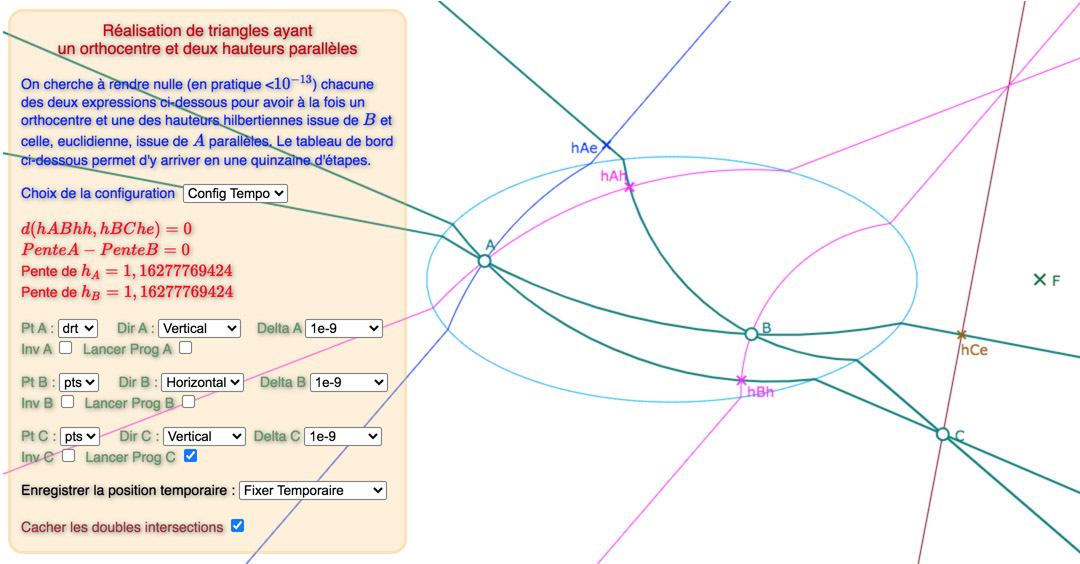
Nous venons de construire des triangles bi-orthocentriques en gérant une double contrainte. Dans cette section, on se propose d’adapter la technique développée pour la recherche de la double orthocentricité à une autre double contrainte, peut-être encore plus originale, que permet ce modèle de Hilbert de la géométrie non arguésienne : l’obtention simultanée d’un orthocentre et de deux hauteurs parallèles !
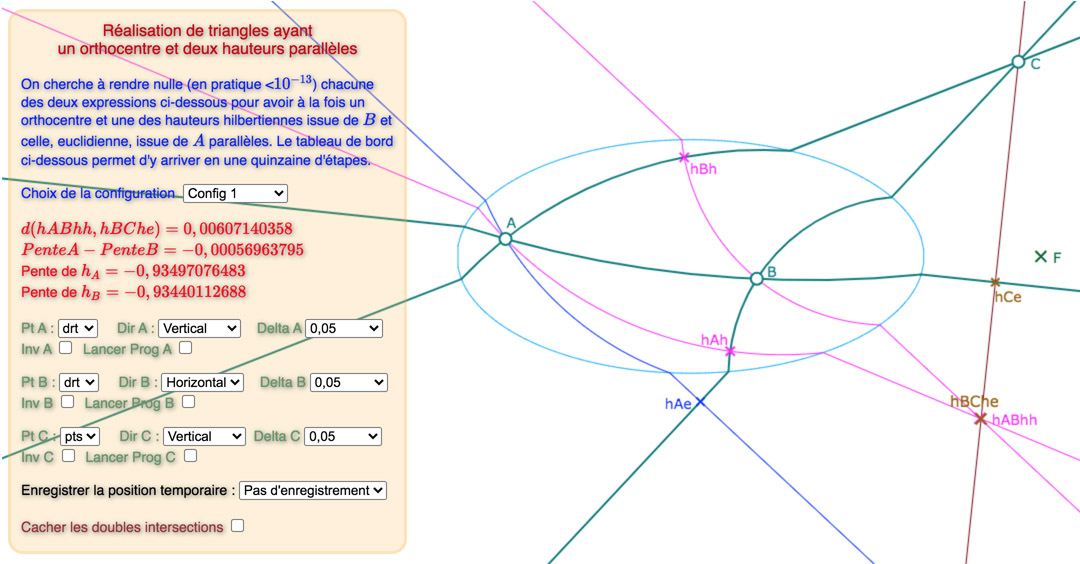
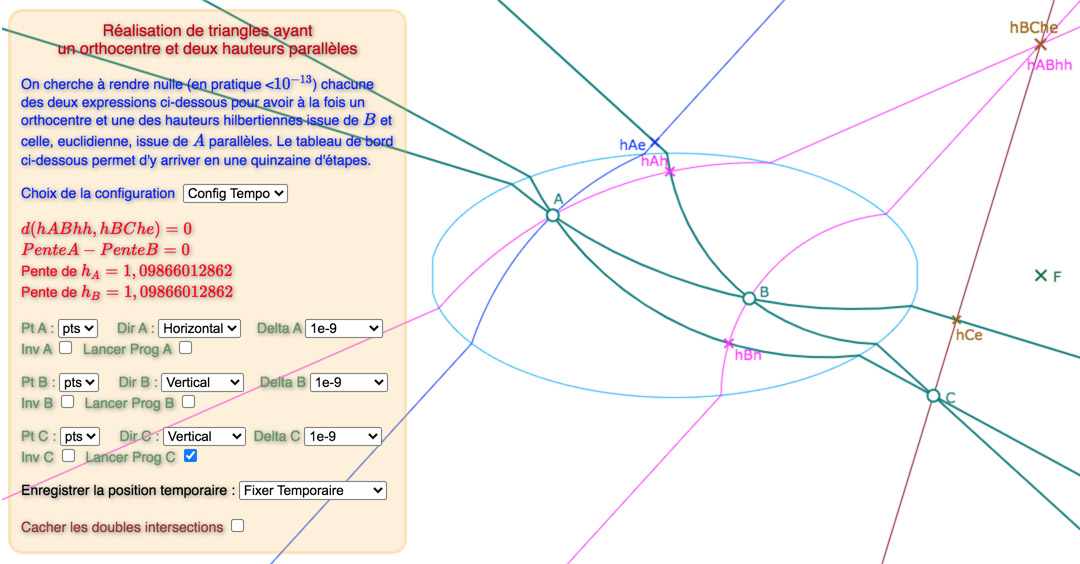
Présentation des résultats
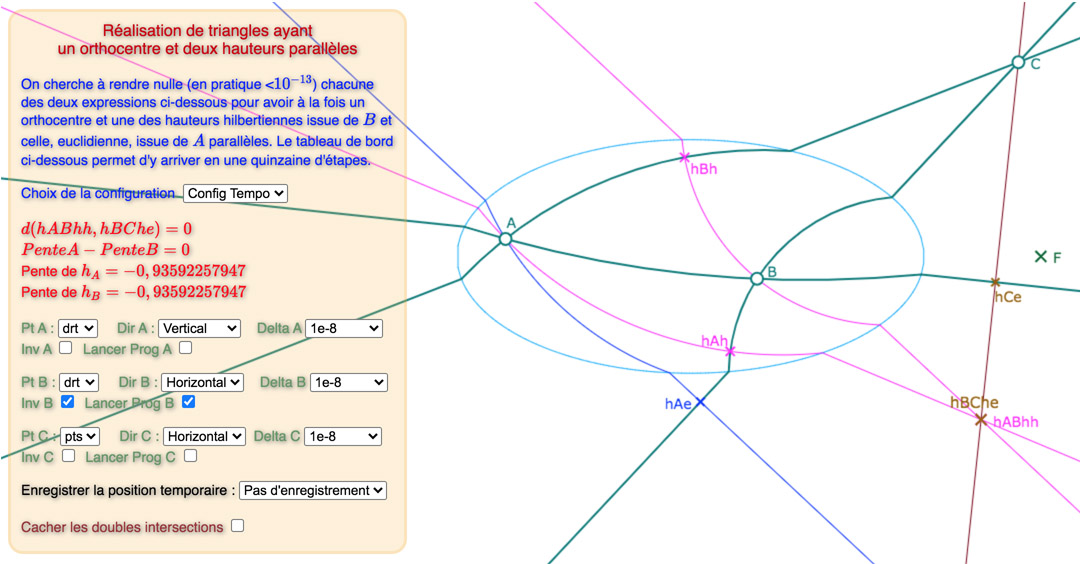
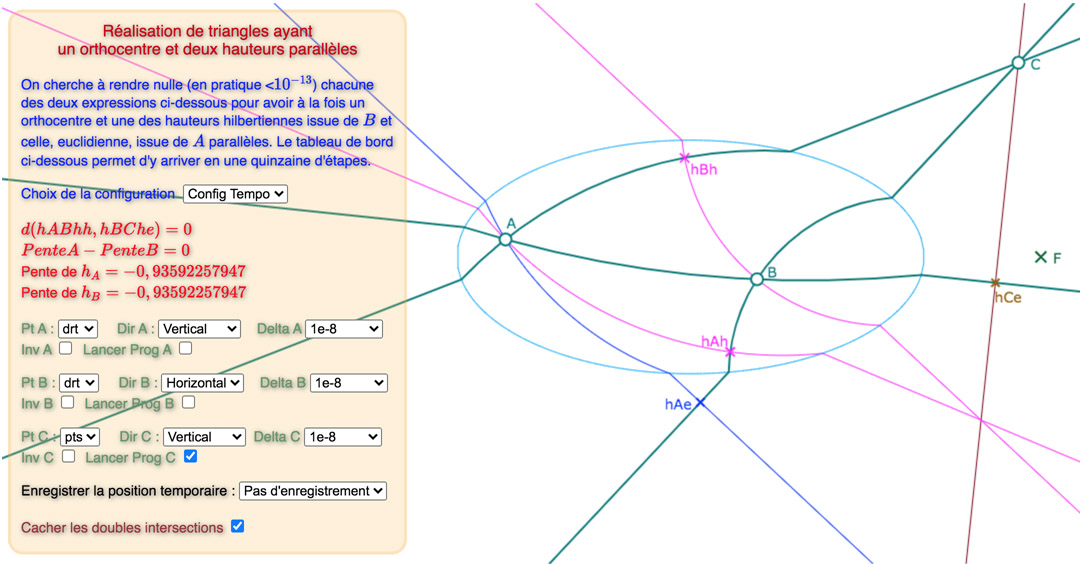
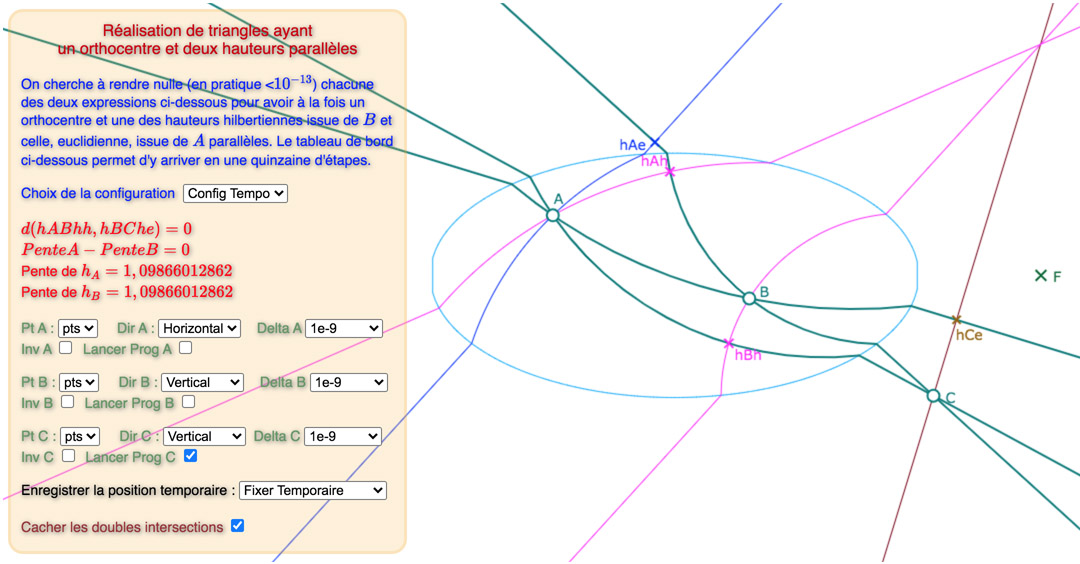
Voici, une galerie de 3 configurations, sur la base du « tableau de bord » déjà utiliséci-dessus : tout d’abord une situation de départ choisie proche d’une solution, puis une solution avec les points des intersections des hauteurs, puis une autre avec ces deux points cachés.
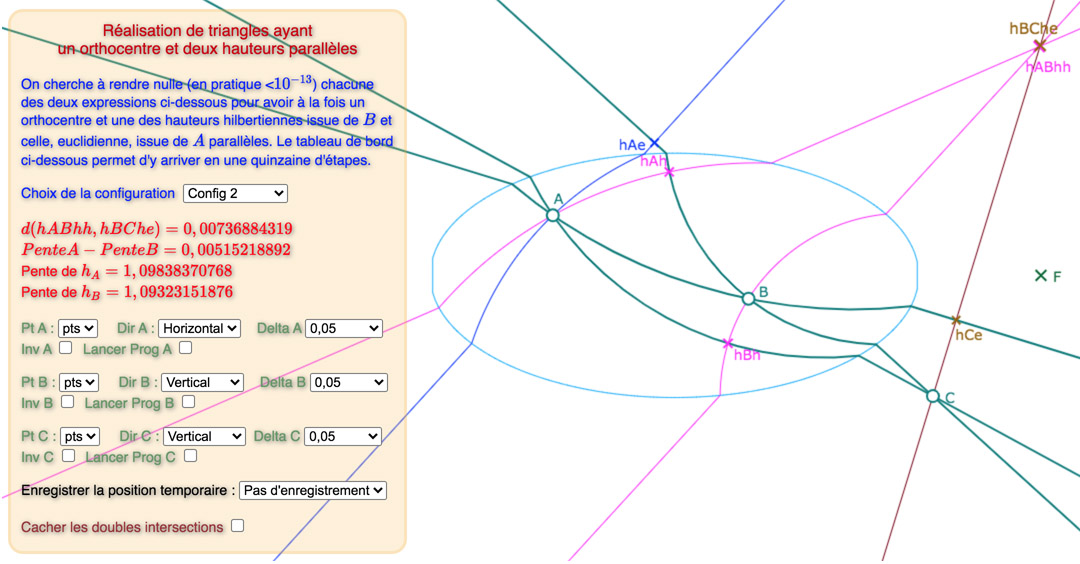
La première configuration est construite autour d’hauteurs parallèles de pente négative, les deux autres, de pente positive.
Prendre le temps de percevoir la différence entre les deux premières illustrations (on peut voir \(hBh\) bouger)
La différence, entre les deux premières illustrations, pour les deux autres configurations est plus claire.
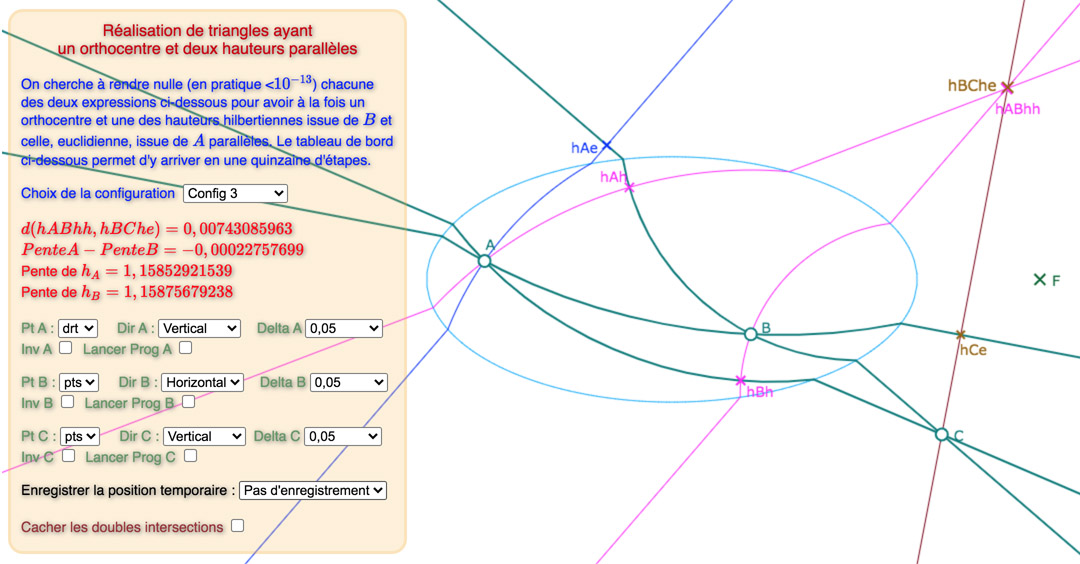
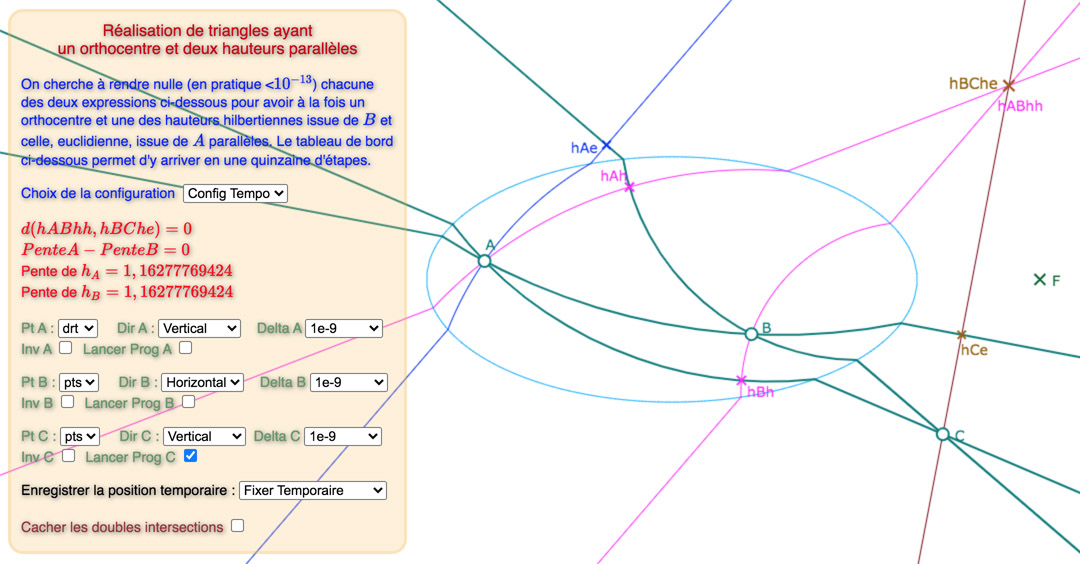
Les configurations 2 et 3
Le commentaire intégré à la figure est assez optimiste en annonçant « une quinzaine d’étapes ». Si pour c’est vrai pour la configuration 1, ce n’est – semble-t-il – plus le cas des deux autres configurations. C’est la raison pour laquelle on propose pour les configurations 2 et 3 la situation de départ et une situation bien plus avancée vers la solution, comme indiqué dans le pop-up des configurations :
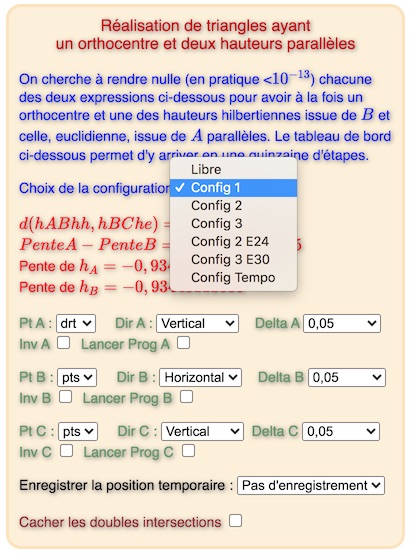
Ces deux étapes avancées E24 et E30 ont les distances et pentes suivantes

On peut s’amuser à essayer d’aller au delà pour obtenir la distance et la différence des pentes toutes les deux nulles (environ 6 étapes dans les deux cas) comme dans la galerie précédente mais rien ne bougera à l’écran car modifier des points d’une amplitude maximale de l’ordre du milliardième de l’unité revient à les déplacer de moins d’un millionième de pixel … On peut aussi concevoir que, graphiquement, déjà dans ces étapes, on est sur les solutions.
Ouvrir la figure correspondante dans un nouvel onglet.
Sur la sensibilité de cette figure
La modification du programme, présentée plus loin, est peut-être à l’origine d’une certaine sensibilité de la figure : quand on clique « Fixer Temporaire » cela peut parfois, à la marge certes, mais justement à partir des étapes avancées proposées, modifier les affichages (typiquement \(10^{-11}\) peut devenir \(0\) ).
Rappel de l’utilisation (détaillée plus haut) : toujours utiliser « Fixer Temporaire » pour évoluer d’une étape à l’autre (et se mettre dès la première étape en « Config Temporaire ») et revenir à « Pas d’enregistrement » avant de faire de nouvelles modifications.
La configuration 1
Sa résolution – sur la même figure que ci-dessus – est plus simple. Voici une chemin possible
La configuration 1 en 13 étapes. On remarquera qu’il suffit d’aller à jusqu’à \(10^{-8}\) dans l’amplitude.
Remarque : pour la dernière étape, le réglage \(drt\) sur le même sommet convient aussi.

La modification du programme
Les pentes étant des nombres, et non pas des points comme dans la double contrainte pour les triangles bi-orthocentriques, il suffit de faire cette simple modification et adapter les autres procédures.
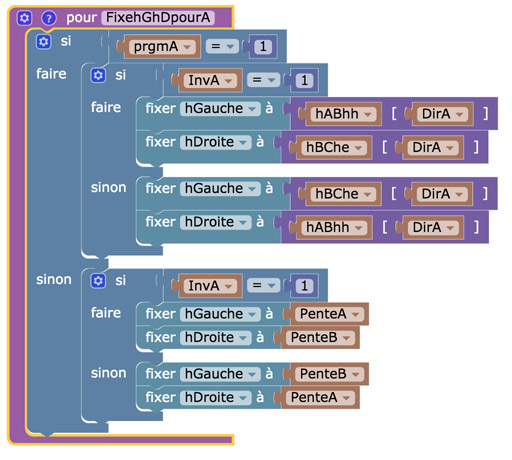
Complément
Depuis, on est allé plus loin, et plus simplement – en conservant l’aspect dynamique pour le cas traité ici.
Consulter cet article sur la bi-orthocentricité avec hauteurs parallèles.