Reprenons le texte de Hilbert sur la congruence des angles dont l’un a un sommet sur l’ellipse avec l’illustration telle qu’elle est proposée dans les premières éditions de ses «Fondements de la géométrie».
Congruence en un point de l’ellipse
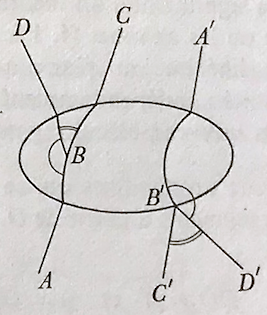
«Enfin il nous faut définir la congruence des angles. Si aucun des sommets des angles à comparer n’appartiennent à l’ellipse, nous dirons que les angles sont congruents s’ils le sont au sens ordinaire du terme. Dans le cas contraire, opérons comme suit :
« Soient\(ABC\) et \(A’B’C’\) des points alignés ordonnés de notre géométrie, \(D\) un point extérieur à la droite \(ABC\) et \(D’\) hors de la droite \(A’B’C’\).
Nous dirons que les congruences suivantes d’angles sont satisfaites:
\(\angle ABD = \angle A’B’D’\) et \(\angle CBD = \angle C’B’D’\) si les angles naturels correspondant sont liés par la proportion
\(\angle ABD : \angle CBD = \angle A’B’D’ : \angle C’B’D’\)
Grace à ces conventions les axiomes (III.1 à 4) sont valables.»
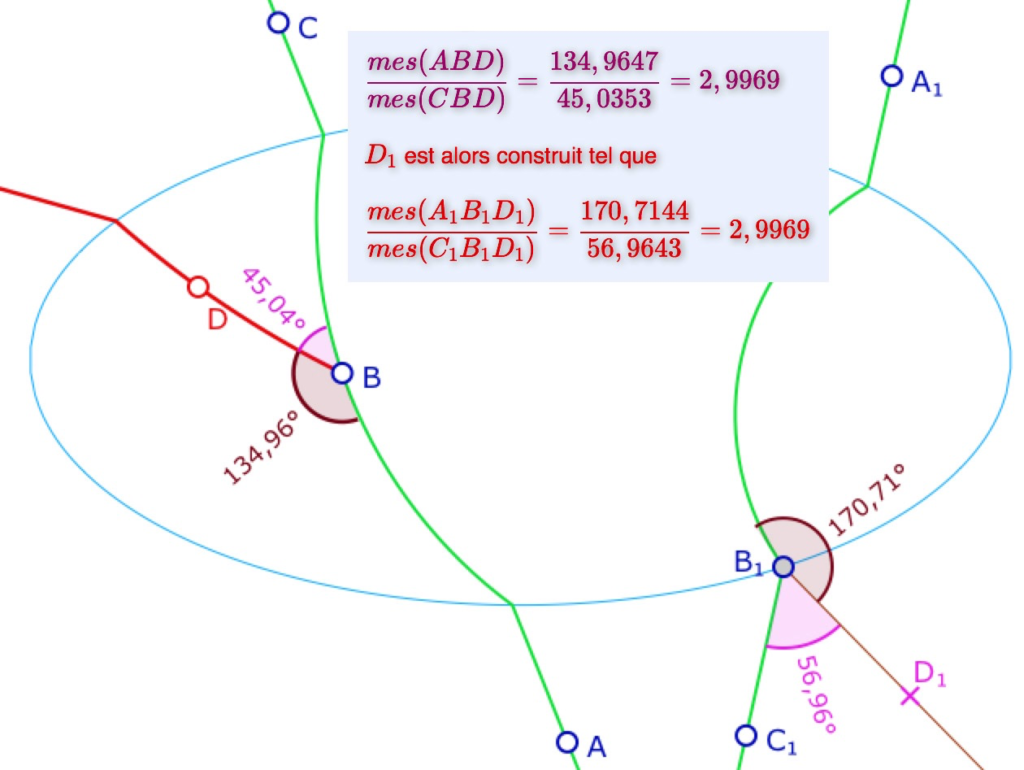
Ci-dessous, la même configuration que celle proposée par Hilbert, rendue dynamique pour l’angle en \(B\) en manipulant le point \(D\).
Dans cette illustration on s’approche de 45° pour \(\angle CBD\) et donc un rapport proche de 3 que l’on reproduit pour construire le point \(D_1\). Cela signifie que la mesure de Hilbert pour l’angle \(\angle C_1B_1D_1\) est celle de l’angle \(\angle CBD\).
Voici deux autres illustrations, à gauche autour de 60° (et d’un rapport proche de 2) et à droite pour l’orthogonalité. Dans ce dernier cas l’illustration est exacte car le point \(D\) est aimanté par l’arc de cercle orthogonal à la droite de Hilbert.
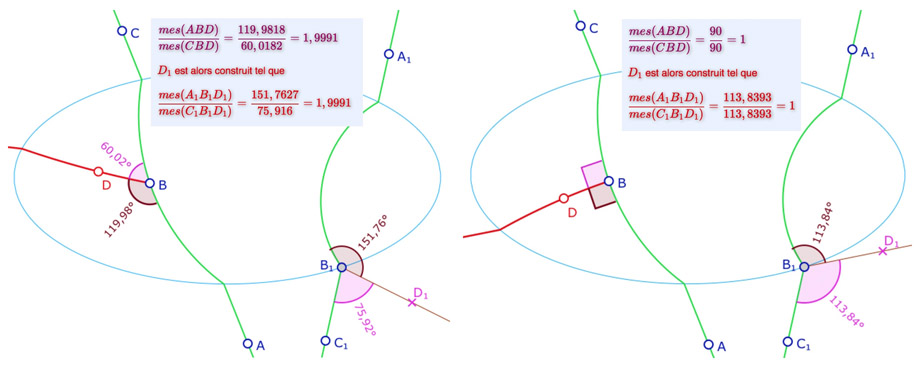
On retient aussi de cette dernière illustration que l’orthogonalité en un point de l’ellipse correspond à la bissectrice euclidienne de l’angle en \(B_1\) de \(A_1B_1C_1\), car l’angle droit correspond à la bissectrice d’un angle plat. C’est tout à fait naturel puisque de chaque côté de la droite \(A_1B_1C_1\), en \(B_1\) il y a deux droits au sens de la géométrie de Hilbert. Plus loin nous utiliserons ce résultat pour réaliser des figures particulières.
Agir sur \(D\) pour modifier l’angle en \(B_1\). On peut agir sur les poignées des deux droites en respectant leurs emplacements respectifs (\(C\) au dessus de l’ellipse, \(A\) en dessous, de même pour \(A_1\) et \(C_1\)). En effet, si la figure est dynamique elle ne reste qu’une figure d’illustration : tous les cas n’ont pas été traités.
Explorer, avec le point \(D\), le cas de l’orthogonalité.
On peut choisir d’ouvrir la même figure « sans restriction » dans un nouvel onglet.
La critique de Moulton
Dès 1902, Forest Ray Moulton a publié un article proposant un modèle euclidien de géométrie non arguésienne, plus simple à mettre en oeuvre et à étudier que celui de Hilbert. Ce sera l’objet des prochaines pages.
Nous nous intéressons ici au début de l’article dans lequel Moulton remet en cause le modèle de Hilbert à propos de sa définition de l’angle non arguésien en un point de l’ellipse.
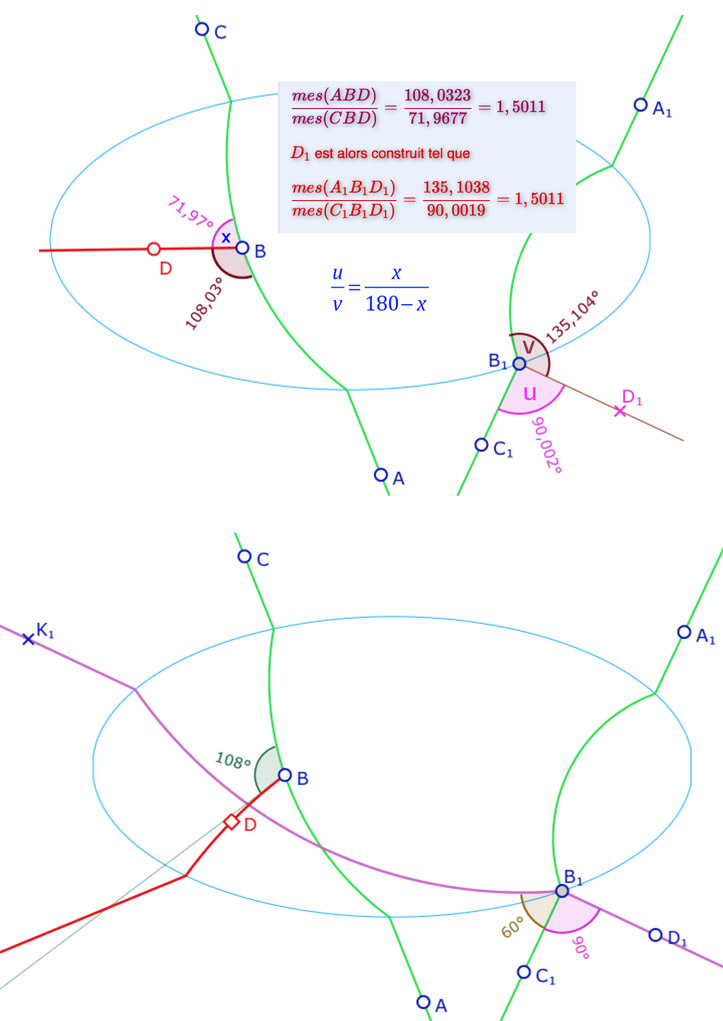
Reprenons la figure précédente en exprimant la H-mesure \(x\) d’un angle \(u=mes(\angle C_1B_1D_1)\), illustrée ci-contre sur une configuration où la H-mesure de \(x=72\) provient d’un angle euclidien proche de l’angle droit. On a ainsi \(x=\displaystyle \frac{180u}{u+v}\), soit, ci-contre, \(x=\displaystyle \frac{180 \times 90}{90+135}=72\).
Or Moulton rappelle que la première conséquence de l’axiome III.4 est que tout angle est congruent à lui-même, et en particulier \((h, k) = (k, h)\). Ci dessus et ci-contre, comme angle euclidien,\(\angle C_1B_1D_1 = \angle D_1B_1C_1\).
Mais si on reprend la définition de la H-congruence entre les angles en \(B_1\) et en \(B\) depuis l’angle \(\angle D_1B_1C_1\), il faut, comme ci-contre, tracer la H-droite contenant \(B_1\) et \(D_1\), c’est la H-droite \((D_1K_1)\) et alors la H-mesure de l’angle \(\angle D_1B_1C_1\) est donnée par \(y=\displaystyle \frac{180u}{u+v}\), soit \(y=\displaystyle \frac{180 \times 90}{90+60}=108\) et donc, avec la propre définition de Hilbert, \(\angle C_1B_1D_1 \neq \angle D_1B_1C_1\).
Moulton en déduit que pour les points de l’ellipse, on n’a pas \((h, k) = (k, h)\) et donc que l’axiome III.4 n’est pas vérifié en les points de l’ellipse.
Bien entendu, Moulton n’a pas détaillé les calculs comme proposés ici, il a juste pointé que la définition de Hilbert aboutissait à ce qu’en un point de l’ellipse on ne pouvait avoir la congruence entre\((h, k)\) et \((k, h)\) . Ci-dessous l’extrait de l’introduction de l’article de Moulton traitant de cette question.


Dans la figure suivante, on peut manipuler la figure inverse de la précédente : on agit sur le point \(D_1\) et la figure construit les deux angles en \(B\) correspondant à \(\angle C_1B_1D_1\) et à \(\angle D_1B_1C_1\). Pour cela utiliser le pop-up en bas du widget.
On peut agir sur les 7 points \(A, B, C, A_1, B_1, C_1\) et \(D_1\) mais on respectera l’organisation générale de la figure sur les positions relatives de ces points. Le point \(D_1\) est aimanté par la bissectrice de \(\angle A_1B_1C_1\) pour que la mesure \(x\) puisse être exactement égale à 90° alors que pour la mesure \(y\) on n’a qu’une approximation pour \(y=90°\), comme c’est le cas à l’ouverture de la figure. Penser à modifier le choix de l’angle exploré par le pop-up menu.
Ouvrir la même figure sans restriction dans un nouvel onglet
Configurations spécifiques pour une mesure cohérente
d’un angle intérieur à l’ellipse de sommet sur l’ellipse
Tout d’abord, dans le cas général, ce qui a été vu précédemment s’applique bien entendu pour l’angle intérieur en \(B\) : les mesures des angles \(\angle PBQ\) et \(\angle QBP\) sont différentes (ci-dessous à gauche). On peut alors se demander à quelles conditions on pourrait avoir ces deux valeurs identiques.

Les deux valeurs seront identiques si et seulement si la bissectrice euclidienne, usuelle, en \(B\) de \(\angle PBQ\) coïncide avec la bissectrice des tangentes en \(B\) des arcs des côtés hilbertiens, soit encore la bissectrice en \(B\) des centres des cercles supports. On peut alors, pour \(P\) donné, construire \(Q\) (quand il existe) pour que les deux angles «H-supplémentaires» soient égaux – ci dessus à gauche – et sur la même figure, pour \(Q\) donné construire \(P\) pour que l’on ait cette égalité d’angle.
Pour que la figure soit manipulable en \(P\) et \(Q\), en pratique ces deux points sont aimantés par les solutions déterminées par l’autre point. Voyons comment ces solutions sont construites, de manière élémentaire.
Dans un premier temps, remarquons que «les bissectrices sont confondues» est équivalent aux fait que les deux angles au centre \(\angle Bc_{BQ}Q\) et \(\angle Bc_{BP}P\) sont égaux. Or, comme les deux cercles passent aussi par \(Q\) ces angles au centre sont égaux ssi les angles angles inscrits \(\angle PFB\) et \(\angle BFQ\) sont égaux (illustration ci dessous à gauche).
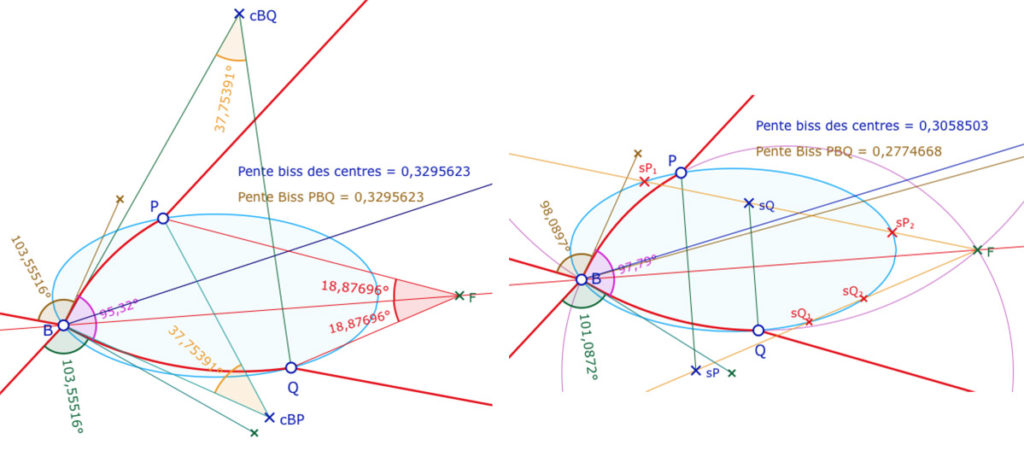
Donc pour \(B\) et \(P\) donnés, les solutions pour \(Q\) sont les intersections – quand elles existent – de l’ellipse de référence et la droite passant par \(F\) et \(s_P\) le symétrique de \(P\) par rapport à la droite \((BF)\). Ci-dessus à droite, ce sont les points \(s_{Q_1}\) et \(s_{Q_2}\). De même on construit \(s_Q\) puis la droite \((Fs_Q)\) qui coupe l’ellipse – quand il y a des solutions – en \(s_{P_1}\) et \(s_{P_2}\), les deux solutions pour \(P\) à \(Q\) fixé.
Dans la figure suivante, \(P\) est aimanté par \(s_{P_1}\) et \(s_{P_2}\) et \(Q\) par \(s_{Q_1}\) et \(s_{Q_2}\). Selon la position de \(B\) une des deux droites \((Fs_P)\) ou \((Fs_Q)\) peut ne pas couper l’ellipse. Il peut donc y avoir des solutions en \(Q\) mais pas en \(P\) ou l’inverse. La figure permet aussi de montrer ou cacher les différentes étapes du raisonnement décrit ici.
Figure sur la configuration pour que les angles \(\angle PBQ\) et \(\angle QBP\) soient égaux
On peut agir sur \(B\), \(P\) et \(Q\). Penser à afficher «la construction» pour voir si les demi-droites coupent l’ellipse ou non. Si «non» il n’y a pas de solution, si «oui» il y a pour \(P\) donné, deux solutions en \(Q\) et/ou pour \(Q\) donné deux solutions en \(P\).
Ouvrir cette figure hors restriction dans un nouvel onglet.
Utilisation de l’orthogonalité en un point de l’ellipse
Autre type de triangle orthocentrique
Dans cette section, on considère une droite \((UV)\) qui coupe l’ellipse en deux points \(R\) et \(S\) et on s’intéresse à la H-orthogonalité à \((UV)\) en ces deux points \(R\) et \(S\). On sait que cette H-orthogonalité correspond à la bissectrice euclidienne de l’angle car dans la relation \(x=\displaystyle \frac{180u}{u+v}\), si \(u=v\), on a bien sûr \(x=90\). Les quatre angles de la bissection d’un même côté de \((UV)\) sont égaux par symétrie de la H-droite \((UV)\) par rapport à la perpendiculaire euclidienne à \(c_{RS}\) passant par le centre \((UV)\) du cercle circonscrit à \(S, R, F\) (illustration de gauche).
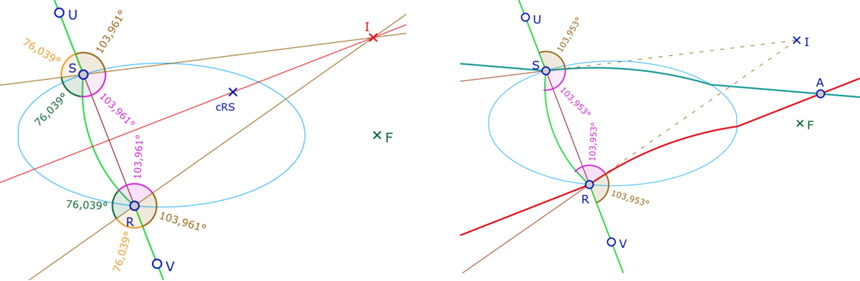
Les deux séries d’angles égaux euclidiens de part et d’autre de \((UV)\) – ci-dessus 76° et 104° – vont correspondre à deux points de vue différents sur la H-orthogonalité.
Cas 1 – Les angles droits intérieurs (ici de 104°). Depuis ces bissectrices euclidiennes, on construit les deux H-droites associées – arcs tangents à \((SI)\) et \((RI)\). Ce sont donc deux H-perpendiculaires à la droite \((UV)\) en les points \(R\) et \(S\). Dans cette situation, on s’intéresse au cas où ces deux droites se coupent en un point \(A\) (illustration de droite). D’après ce qui précède, ce sont les angles \(\angle RSA\) et \(\angle SRA\) qui sont droits (et pas \(\angle ASR\) ni \(\angle ARS\)) ainsi que les angles \(\angle USA\) et \(\angle VRA\) (et non pas \(\angle ASU\) ni \(\angle ARV\)).
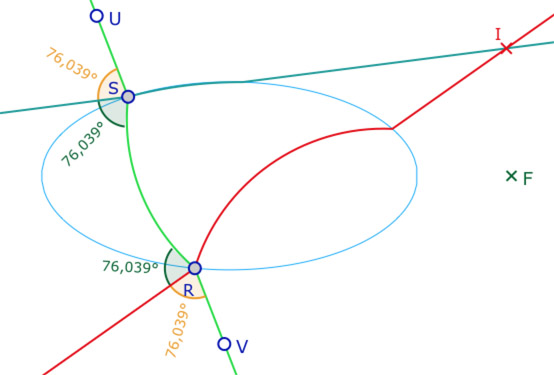
Cas 2 – Les angles droits extérieurs (ici de 76°)
Dans ce cas, la partie extérieure à l’ellipse des bissectrices sont les droites support des H-perpendiculaires. Ce sont donc deux autres orthogonalités à \((UV)\) en les points \(R\) et \(S\). Ces H-droites sont alors sécantes en \(I\).
Cette situation est toutefois moins naturelle car les angles du côté de \(I\), \(\angle RSI\) et \(\angle SRI\) ne sont pas droits puisque l’orthogonalité est de l’autre côté de la droite \((UV)\). Difficile de dire que \(S\) est le pied de la perpendiculaire issue de \(I\). Aussi, pour ce qui va suivre, si l’approche est théoriquement fondée, d’un point de vue géométrique, on préfèrera l’approche du «cas 1».
Triangle orthocentrique dans le « cas 1 »
On se donne un point \(B\) sur la demi-droite \([SU)\) et un point \(C\) de la demi-droite \([RV)\). Les H-droites \((AS)\) et \((AR)\) sont deux H-hauteurs issues de \(C\) du H-triangle \(ABC\).
On cherche alors s’il existe des configurations de \(ABC\) tel que ce triangle soit orthocentrique. Pour simplifier la construction, on se limite au cas où les côtés du triangle issus de \(A\) ne rencontrent pas l’ellipse. Ainsi les pieds des hauteurs \(hCa\) et \(hBa\) sont extérieurs à l’ellipse, et la construction des deux hauteurs sont de simples constructions géométriques. On peut alors ajuster \(B\) et \(C\) pour que – heuristiquement – les deux hauteurs issues de \(B\) et \(C\) se coupent sur l’une des deux hauteurs issues de \(A\).
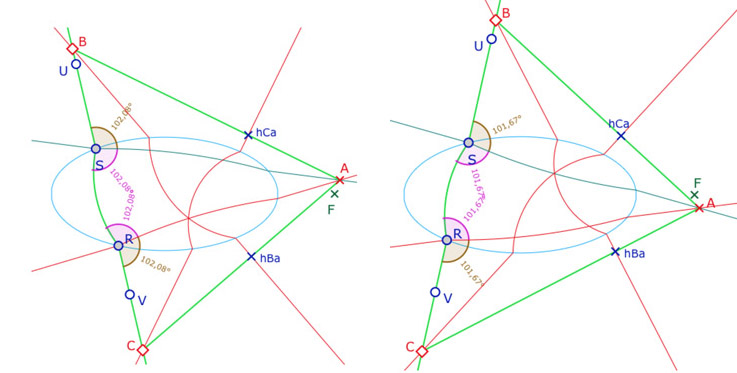
On se sert des points \(U\) et \(V\) comme poignées de manipulation générale de la figure. Il faut en effet modifier l’orientation de la droite euclidienne \((UV)\) pour que l’orthocentre soit sur \((AR)\) ou \((AS)\).
Triangle orthocentrique dans le «cas 2»
On note \(hBi\) et \(hCi\) les pieds des hauteurs issues de \(B\) et \(C\).
Ci-dessous à gauche le cas – toujours obtenu de manière heuristique – où l’intersection des hauteurs issues de \(B\) et \(C\) se coupent sur la hauteur \((SI)\) issue de \(I\). A droite l’orthocentre est sur l’autre hauteur issue de \(I\), la droite \((RI)\).
Remarque : on note les hauteurs \((SI)\) et \((RI)\) (et non pas \((IS)\) et \((IR)\)) car l’orthogonalité étant à gauche, c’est dans ce sens de parcours des droites que doit être pensée l’orthogonalité.
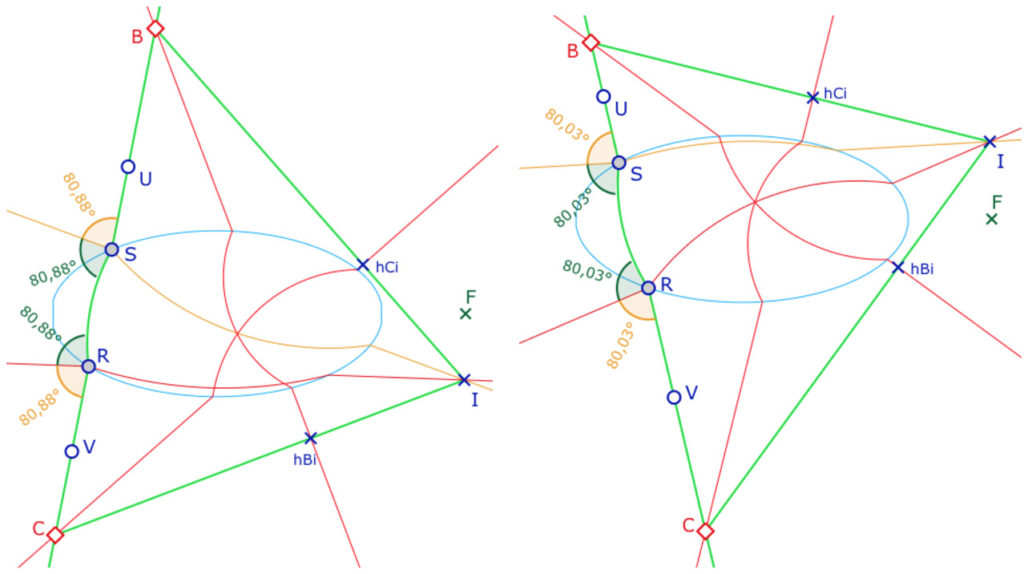
Là encore, on ne s’intéresse – pour une question de réalisation élémentaire – qu’aux cas où les côtés issus de \(B\) et \(C\) ne coupent pas l’ellipse : les pieds de hauteurs \(hBi\) et \(hCi\) sont à l’extérieur de l’ellipse.
Ayant obtenu ces deux types de triangles orthocentriques, on peut placer les deux constructions dans une même figure, et chercher une configuration dans laquelle les deux triangles \(ABC\) et \(IBC\) sont simultanément orthocentriques pour chacune des deux approches de l’orthogonalité en un point de l’ellipse. C’est le cas dans l’illustration ci-dessous (à gauche), avec les hauteurs issues de \(A\) et \(I\) et de «pieds» le point \(S\) pour les deux triangles.
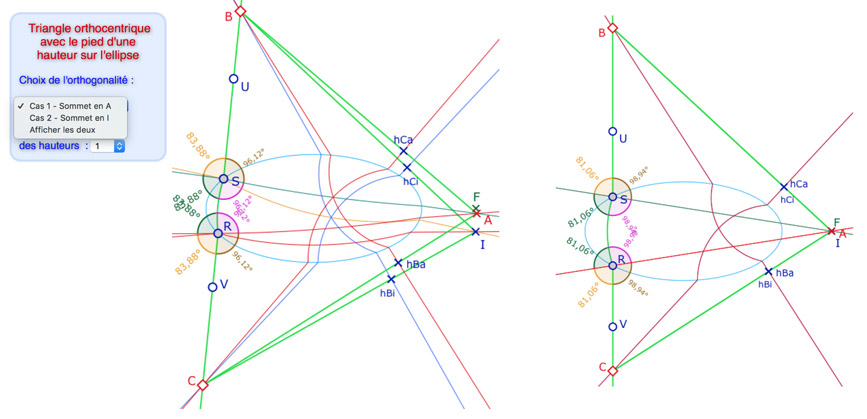
Enfin, si la droite \((UV)\) est parallèle à l’axe des ordonnées, les bissectrices euclidiennes sont les droites passant par \(F\), ce sont aussi les H-droites associées : les deux conceptions de l’orthogonalité sont confondues, tout comme les points \(A, I\) et \(F\) (illustration de droite).
Orthogonalité en un point de l’ellipse et triangle orthocentrique associé
Explorer les deux choix d’orthogonalité en \(R\) et \(S\) : on agit sur \(U\) et \(V\) pour l’orientation de la droite puis sur \(B\) ou \(C\).
Remarque : \(B\) et \(C\) sont sur objet des demi-droite, donc agir sur \(U\) ou \(V\) déplace \(R\) ou \(S\) même à orientation fixe (par aspect affine interne au logiciel).
Préférer lancer la même figure, non « responsive », dans un autre onglet.