Les micro-mondes et leurs macro-constructions
Le terme micro-monde a plusieurs acceptations, selon le contexte plus ou moins informatique ou didactique par exemple. Pour la géométrie dynamique, il s’agit de cette capacité à enrichir l’environnement proposé initialement en réalisant un corpus de macro-constructions sur un thème donné.
On peut ainsi développer des micro-mondes sur les cercles, les coniques, les espaces vectoriels, mais aussi, et c’est ce qui nous occupe ici, sur d’autres géométries qu’euclidiennes qui peuvent avoir des modèles euclidiens, et même éventuellement finis comme nous le proposons dans le menu DP.
La qualité d’un logiciel de géométrie dynamique peut s’évaluer sur plusieurs critères, comme son rapport à la modalité, sa capacité à engager la création d’objets à l’intérieur de la création d’autres objets (engagement direct), et la qualité des micro-mondes qu’il permet de construire.
Les premières réflexions, et l’exigence de qualité de l’expérience utilisateur sur ces sujets ont été initiées par Jean Marie Laborde créateur de Cabri-géomètre. Les qualités de micro mondes peuvent être subtiles et internes au logiciel, dans leur capacité à utiliser implicitement les éléments constituants d’autres objets.
Par exemple, parmi les nombreuses subtilités développées dans Cabri-géomètre, Jean Marie Labordea introduit la possibilité que les macros puissent avoir des objets finaux existant dans des situations disjointes selon les conditions initiales, ce qui a été repris par DGPad, et permet de réaliser une macro « cercle elliptique » que ce cercle soit représenté par un cercle euclidiens ou deux arcs de cercles.

DGPad dispose de deux types de macros (icone « clé à molette – marteau » du tableau de bord) , celles, dites de bibliothèque, intégrées dans la logiciel et celles dites personnelles créées par l’utilisateur. Ce sont essentiellement celles-ci que nous utiliserons dans la suite : ce seront les macros des micro-mondes étudiés.
Dans les figures de ce site, les macros personnelles sont livrées dans les figures, elles n’ont pas à être faites par le lecteur, ni même à être téléchargées. Cela aurait pu être un quatrième type de figures que de proposer que le lecteur enrichisse lui-même le micro monde qu’il étudie. Cela n’a pas été proposé pour éviter trop de technicité.
Un premier exemple de macros personnelle euclidienne
Nous commençons par tester une macro qui permet de construire « manuellement » (ie pas par programme, en appliquant plusieurs fois la macro) les premières itérations de la fractale de Pythagore. Dans la figure suivante, cliquer sur l’icone des macros, puis à nouveau sur PythaPoly, et quand apparaît l’attente «Polygone», cliquer sur les polygones rouge et bleu successivement …
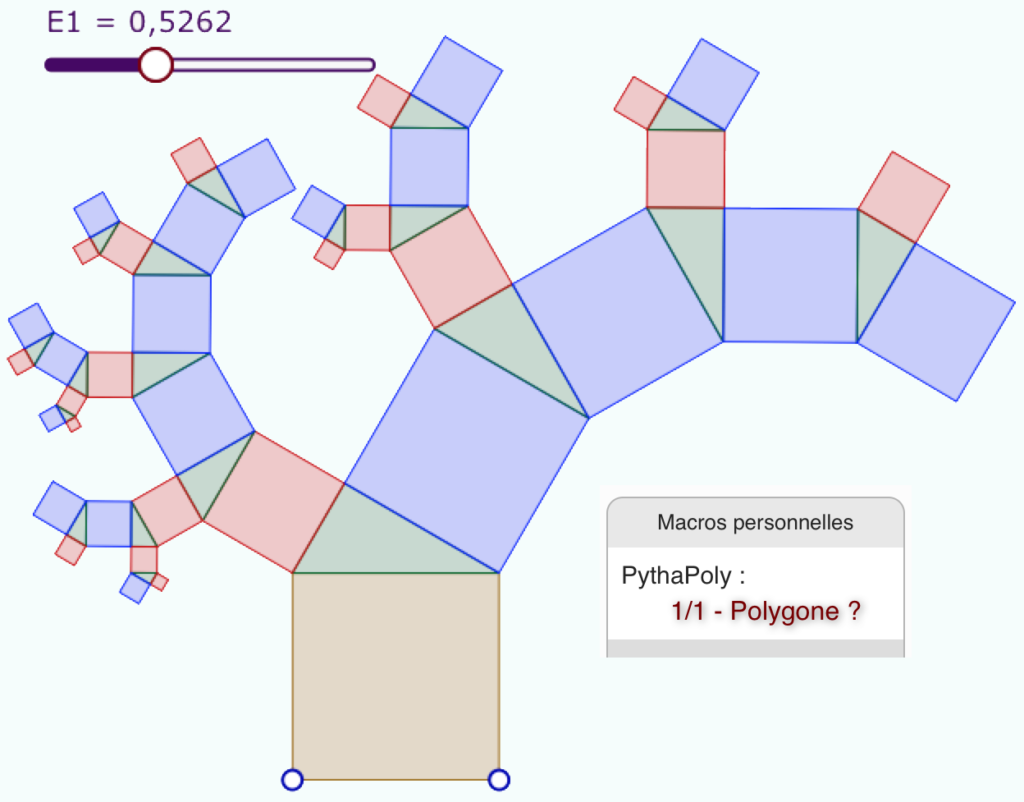
ci-après avec la macro à utiliser.
Penser à diminuer la taille du carré initial en agissant sur le second point rouge du carré.
En mode « consultation » (aucune icone du tableau de bord sélectionnée) on déplace la figure à la souris
Pour quitter le mode macro il faut cliquer une fois sur l’icone des macros pour quitter la macro en cours, et une seconde fois pour quitter le mode macro. On revient alors en mode consultation (aucune icone sélectionnée). Et on peut alors agir sur le curseur. On peut aussi quitter plus vite le mode macro simplement en cliquant sur un autre outil
Note sur l’engagement direct : la figure serait plus en « engagement direct », si on pouvait déplacer le sommet du triangle vert à la souris (ou au doigt) au lieu d’agir sur le curseur. Mais il aurait alors fallu sélectionner ce point à chaque application de la macro. On a choisi cette version différente pour n’avoir qu’un polygone à cliquer.
Second exemple sur les cercles avec deux macros différentes
Dans la figure suivante, la macro 2CT 1C2pts construit, à partir d’un cercle et de deux points, les deux cercles tangents à ce cercle passant par les 2 points. La macro 4CT 2C1pt construit les 4 cercles tangents à deux cercles passant par un point. Penser à mettre le point et un cercle dans l’autre comme à droite dans l’illustration suivante.
Dans la macro sur Pythagore, comme il n’y avait qu’un objet à sélectionner, on ne voyait pas qu’il faut respecter l’ordre des objets initiaux proposés par la macro.

Quand la macro s’est effectuée, il faut la quitter le mode macro (deux clics sur l’outil macro du tableau de bord ou un clic sur un autre outil, comme la flèche) pour pouvoir reprendre la main sur les objets de base et les déplacer.
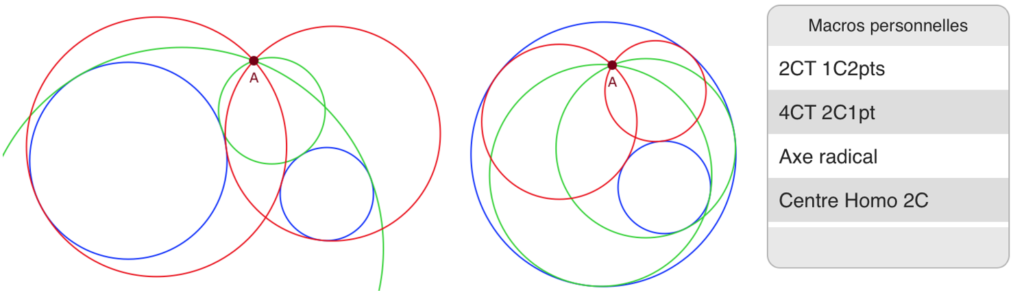
Attention : les centres des cercles disparaissent (ils sont cachés) après l’utilisation des macros. On peut les faire réapparaître avec l’outil «gomme» et en cliquant sur les centres. Pour supprimer les cercles – entre l’utilisation des deux macros – on utilisera la flèche retour à droite : un seul clic sur la flèche supprime tous les éléments produits par la macro.
On peut tester sur cette figure l’utilisation de divers outils du tableau de bord (gomme, corbeille – sur les objets produits par les macros – ou autres. Si on rencontre un problème, il suffit de recharger la figure dans l’iframe.
Les macros des GNE utilisées dans les menus suivants
Les macros à utiliser seront souvent propres à chaque figure comme ci-dessous sur le disque de Poincaré.
Comme nous serons, dans trois des cas proposés dans ce site, dans un modèle délimité par un cercle – que ce soit dans le disque de Poincaré, dans le modèle elliptique, ou en géométrie euclidienne bornée, le premier objet à montrer sera ce cercle horizon. Pour une droite hyperbolique, on montrera deux points, comme indiqué dans les attentes. Par contre, pour une perpendiculaire hyperbolique, le second objet à montrer est un arc de cercle – la droite hyperbolique – et c’est repéré comme «de type cercle» donc cela attend un (arc de) cercle , puis un point.

Dans d’autres situations, des macros d’environnements différents pourront être regroupées pour explorer s’il existe des propriétés propres aux modèles à la rencontre de ces deux micro-mondes. Ci-dessous deux environnements qui ont les mêmes droites, simplement à une nuance conceptuelle près sur laquelle nous reviendrons.

Plus classiquement, quand on sera allé assez loin dans une géométrie, on travaillera sur un corpus de macro-constructions qui seront regroupées comme ci-contre dans des dossiers thématiques. Rappelons que généralement, pour éviter la surcharge cognitive, les figures contiendront uniquement les macros utiles à la construction envisagée.