Comme signalé dans les autres pages, le calcul détaillé des rayons des cercles de pavages est abordé dans cet article de blog. Ainsi on a \(ch_{46} = \displaystyle \sqrt{3} \)
Le rayon du cercle de pavage de \(P(4,6)\) vérifie \(ch_{46} > 1,73\) est donc nettement plus grand que celui de \(P(4,5)\) puisque \(ch_{45}\) est approximativement égal à \(1,38\). Pour arriver à mettre 6 carrés sur la surface, il va falloir modifier la démarche utilisée dans les deux pages précédentes. Par contre pour placer 4 hexagones orthogonaux de \(P(6,4)\), ce sera un peu plus facile. Commençons par \(P(4,6)\).
Un carré d’angles aux sommets 60°
On commence par un premier carré, et l’on voit qu’il peut prendre beaucoup de place sur la feuille principale de la surface
Construction de base d’un carré pour explorer la situation
Placer trois carrés d’angles 60°
Pour placer trois carrés consécutifs, entièrement sur la pseudosphère hyperbolique, il n’y a qu’une possibilité (pour les valeurs de \(p\) que l’on a retenues) : placer le centre du cercle sur la. feuille précédente de la feuille principale – ou la suivante c’est symétrique. C’est ce que l’on fait dans la figure suivante : le point \(O\) continue de parcourir le même cercle euclidien (une PSH-équidistante) mais sa longitude est comptée comme appartenant à l’intervalle \([-3\pi, -\pi]\) au lieu de \([-\pi, \pi]\). On obtient dont quelque chose comme cela, a priori un peu délicat à lire sur la surface.
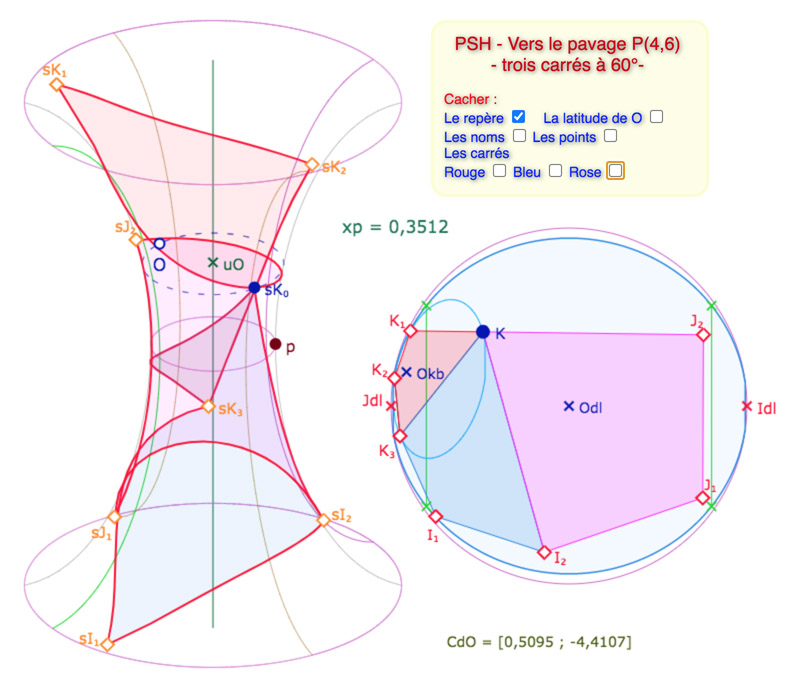
Trois carrés contigus de P(4,6) avec le centre du cercle sur la page avant la page principale
Chaque carré, même le premier – rouge – est relativement étendu sur la surface. On peut voir dans cette illustration, les deux traversées de la frontière (verte) de la feuille principale des segments \([sK_0 \; sK_1]\) et \([sK_3 \; sK_0]\).
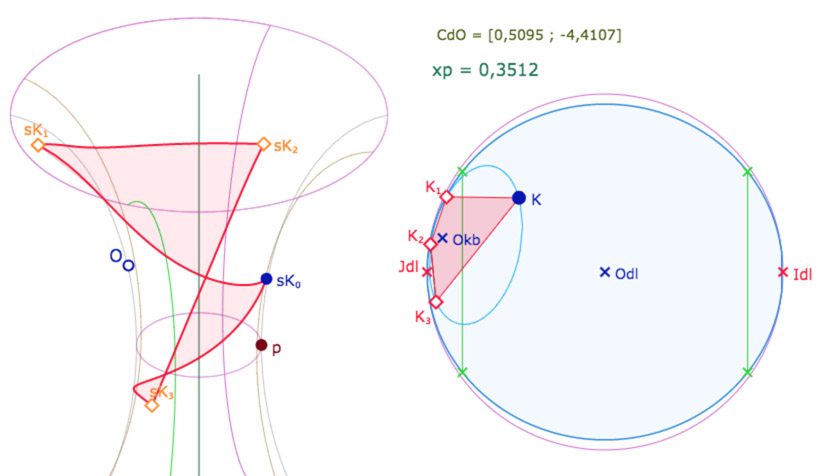
Et toujours dans la même configuration, chaque carré vu de dessus : on voit mieux l’amplitude longitudinale de chaque carré,
ainsi que le franchissement de la feuille principale. Dans cette configuration aucun carré ne se déploie sur plus d’une feuille.
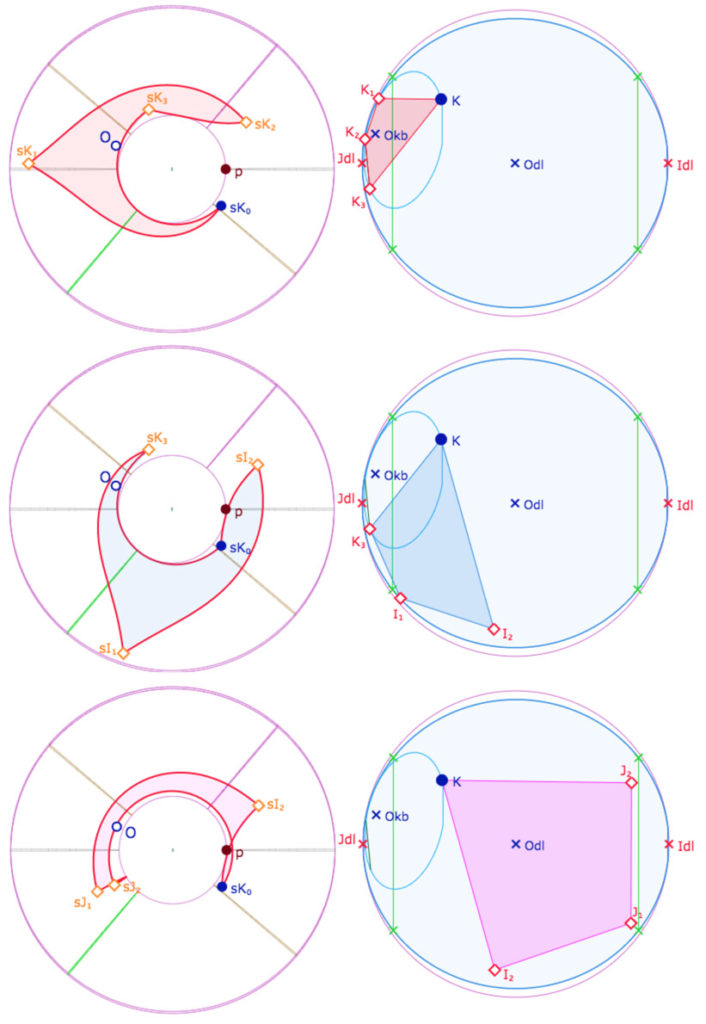
Manipuler la figure associée
Dans cette figure on peut déplacer \(O\) ainsi que sa latitude \(u_O\) en la rendant visible.
Ajuster la figure en déplaçant le point \(K\) sur le KB-cercle de pavage.
Penser aussi à agir sur la paramètre \(p\) car cela ne sera plus possible dans la figure suivante.
Préférer ouvrir cette figure, sans restriction, dans un nouvel onglet.
Les 6 carrés autour du point K
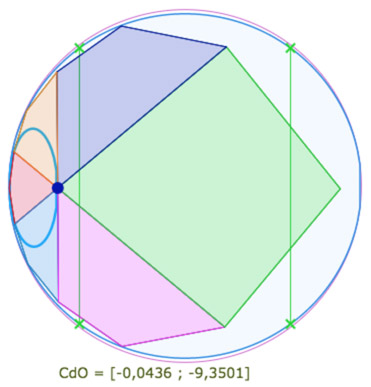
Pour que les trois derniers carrés rentrent entièrement sur la surface en même temps que les trois premiers, le changement de feuille du centre du cercle de pavage ne suffit plus. Il faut baisser le paramètre \(p\) en dessous de la valeur minimale proposée initialement par la figure (\(0,25 \le p \le 0,75\)). Comme toute la figure est construite à partir de l’expression \(xp\), celle-ci est rendue modifiable directement à la main.
Dans la suite des illustrations, elle est réglée à 0,22. On peut essayer aussi 0,23 mais c’est moins simple de trouver des configurations qui font entrer tous les carrés sur la surface.
Une autre condition est que le centre du cercle, le point \(O\), algorithmiquement placé sur la feuille « -1 », soit désormais assez proche de la frontière avec la feuille précédente, la feuille « -2 ». Sur l’illustration ci-contre, la longitude de \(O\) est de -9,35 alors que \(-3\pi\) est de l’ordre de -9,42.
Comme on l’a fait pour les constructions des autres pavages, avant la manipulation de la figure, on propose quelques illustrations des possibilités de manipulation. On notera éventuellement quelques variantes d’affichage.
Première illustration autour du pavage P(4,6) sur la PSH, pour p=0,22
Tout d’abord, contrairement à la situation précédente, parce que \(p\) est petit, un carré peut régulièrement s’enrouler sur plus d’un tour de la surface, ce qui rend la lisibilité de la figure moins simple et nécessite de tourner la pseudosphère pour mieux appréhender la situation.
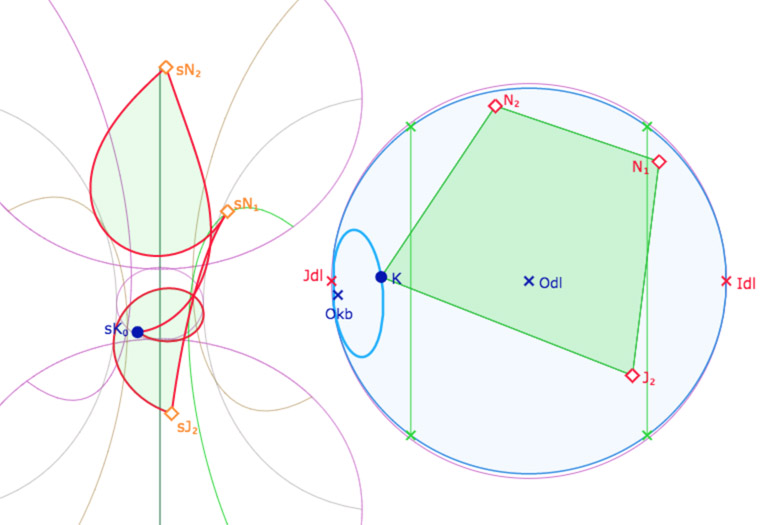
Exemple d’un carré qui s’enroule sur plus d’un tour de la PSH
On poursuit par des deux carrés qui vont faire un demi pavage avec celui-ci. Le suivant s’enroule lui aussi sur plus d’un tour.
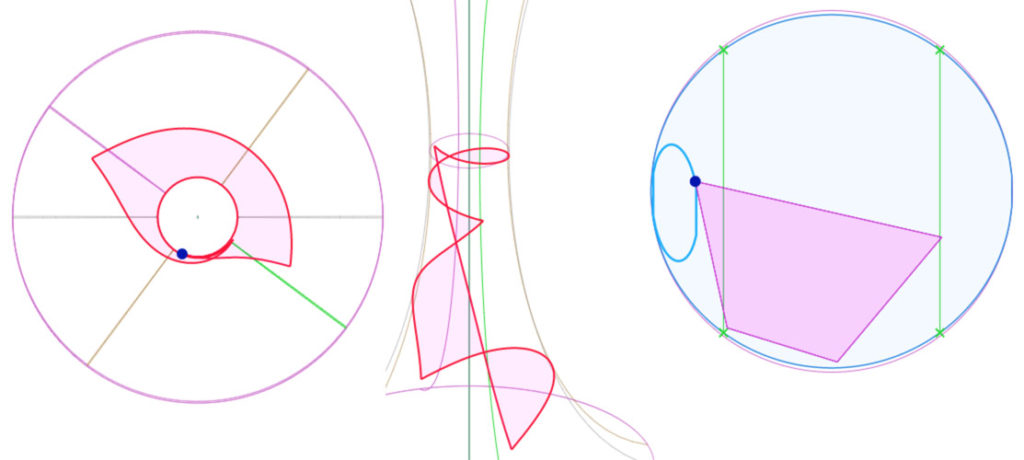
Ce qui donne, au final un demi pavage de ce type, qui recouvre un peu plus que deux tours …
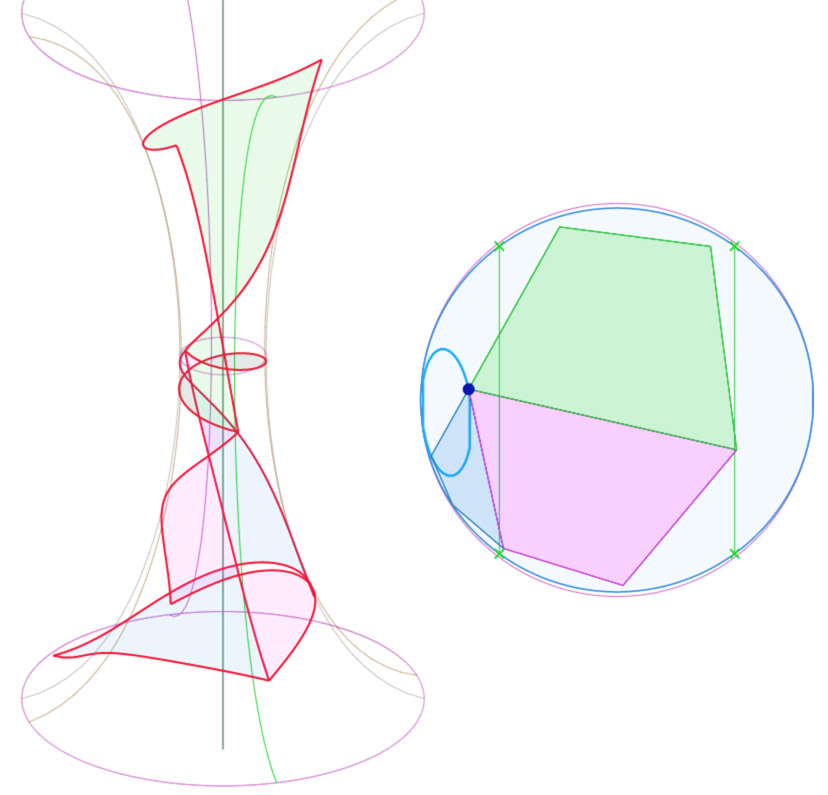
Ce qui se voit (un peu) mieux avec la vue de dessus, en regardant les sommets vert et bleu adéquats.
Cela serait plus clair avec la différences des longitudes, mais cela aurait été moins esthétique …
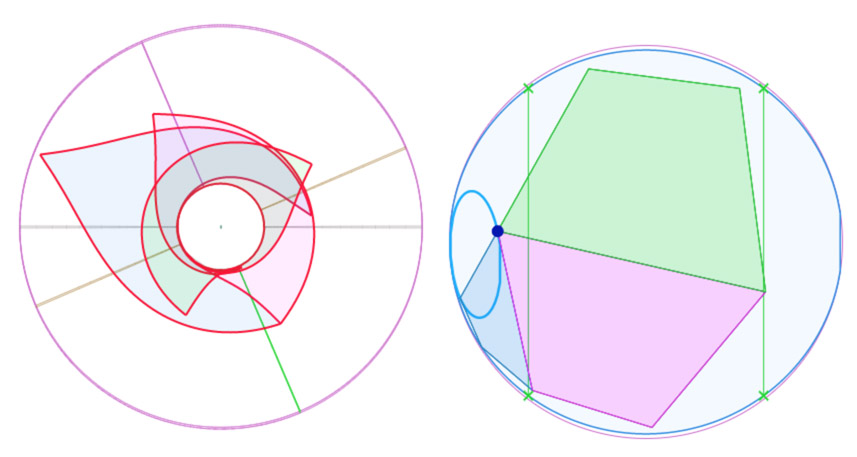
Autre illustration – version « ailes de moulin »
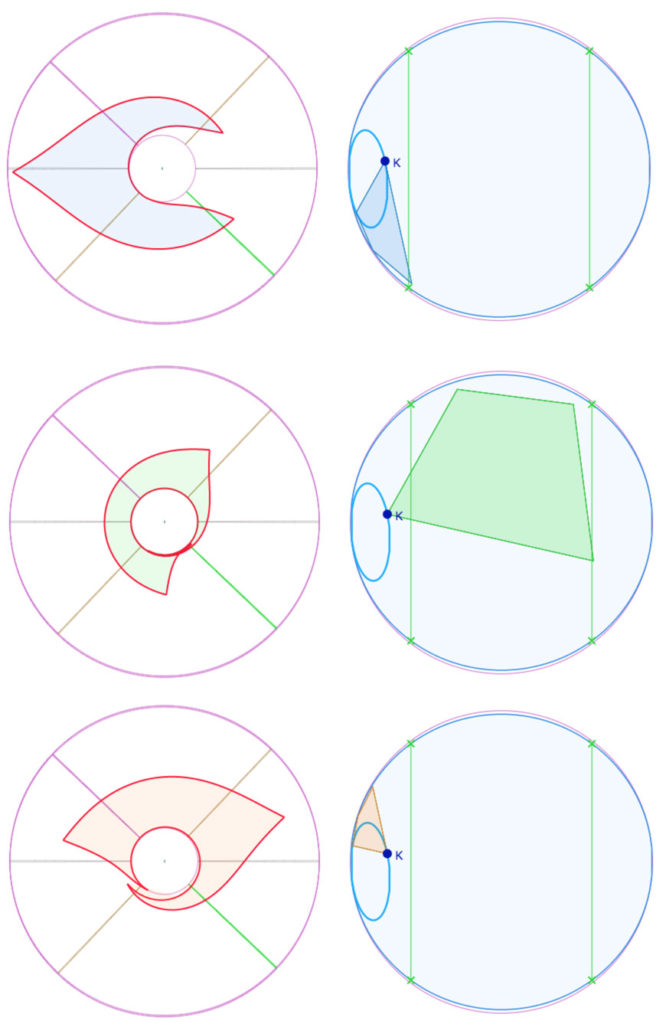
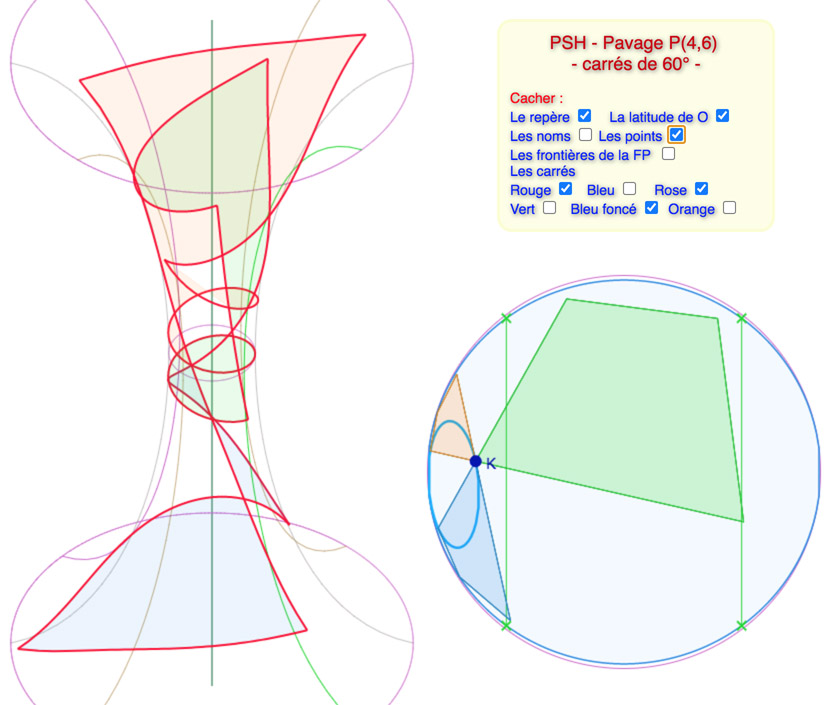
Manipulation de la figure du pavage P(4,6) sur la PSH
En voici une copie d’écran. On aura compris qu’il faut jongler avec les différentes options possibles, comme illustré ci-dessus pour y voir quelque chose.
Par ailleurs – ce qui n’a pas été illustré ci-dessus – on peut aussi tenter de changer la valeur de \(p\) (de 0,01). (Outil calculatrice, rentrer la valeur, avec un point décimal, et confirmer par le « bouton vert »)
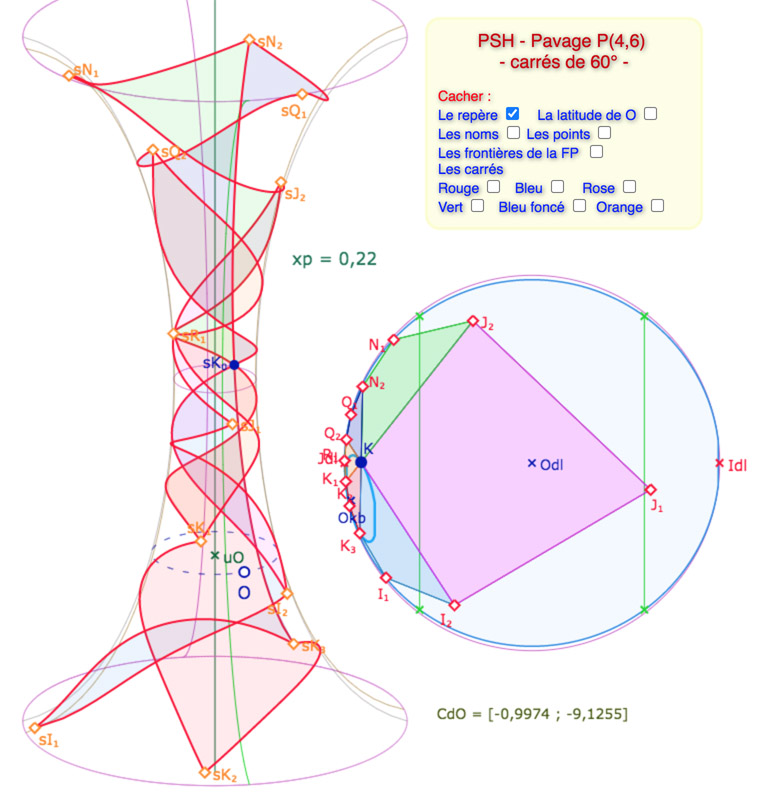
La figure est trop grande (trop haute) pour être proposée dans une iframe. On l’ouvrira dans ce nouvel onglet.
Penser à être en mode consultation (aucun outil sélectionné) pour changer l’orientation ou tourner la pseudosphère à la souris ou au doigt.
Un hexagone orthogonal
Pour réaliser le pavage P(6,4) autour d’un point, on commence comme dans les autres cas, par un premier hexagone. Il est donc orthogonal, ce qui signifie entre autre que son aire est égale à \(\pi\), puisque l’aire d’un hexagone est égale à \(4\pi – somme \, des \, angles\), soit ici \(4\pi – 6 \times \frac{\pi}{2}\). L’hexagone orthogonal hyperbolique – qui est constructible à la règle et au compas (résultat de Bolyai), puisque c’est le cas de \(ch(r_{64})=\sqrt{3}\) – réalise ainsi une hexagonature de \(\pi\), ce qui n’existe pas – à la règle et au compas – en géométrie euclidienne.
Manipuler cette première figure vers P(6,4)
Mêmes consignes que dans les figures précédentes d’un premier polygone de pavage : tous les paramètres sont modifiables.
Le pavage P(6,4)
Tout d’abord, comme pour P(4,6), on place le centre du cercle sur la feuille précédente à la feuille principale. Par contre il n’est pas nécessaire de diminuer le paramètre associé à \(p\) en dessous de la valeur obtenue par sa mobilité dans la figure (0,25), ce qui permet d’explorer un peu plus librement quelques configurations spécifiques.
Une première configuration avec deux hexagones « verticaux »
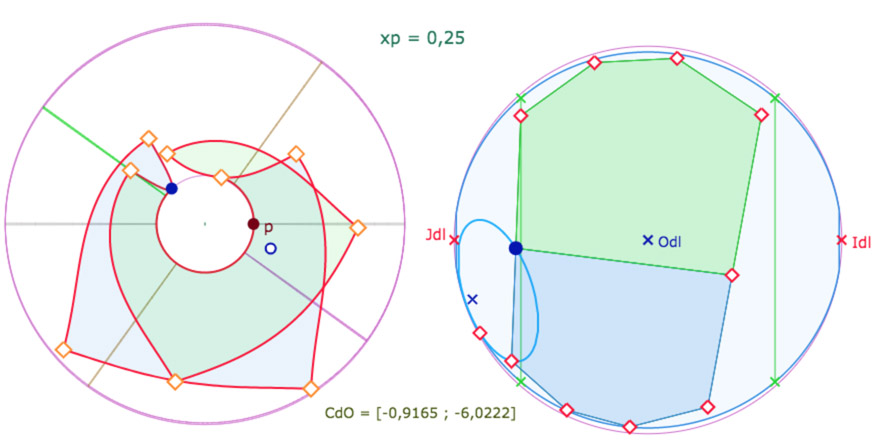
Deux vues de la même configuration , de dessus et de face. On peut suivre le contour des deux hexagones en partant
par exemple du sommet de l’hexagone vert sur la frontière de la feuille principale, ou tout simplement du point K.
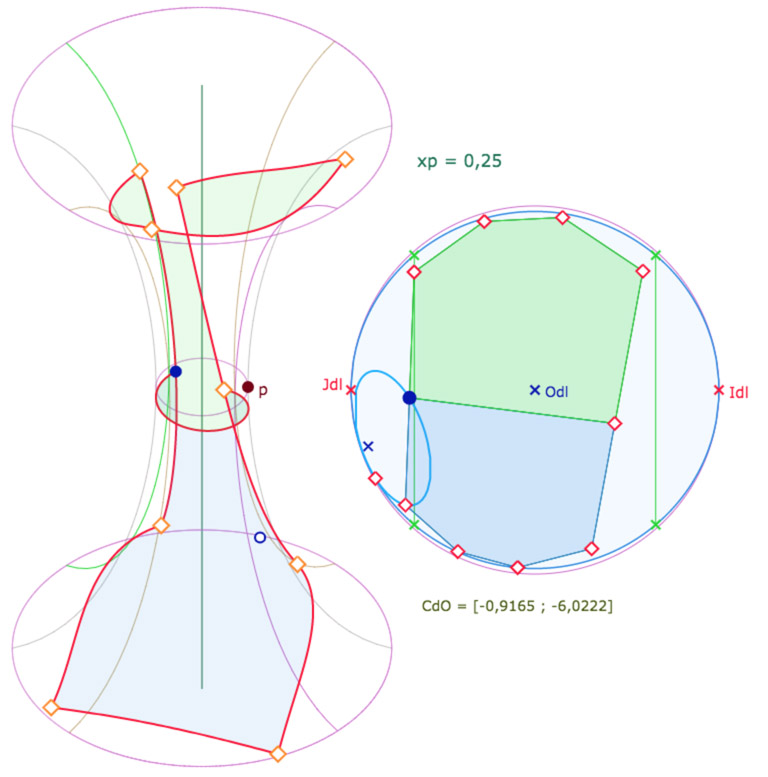
Une configuration en « ailes de papillon »
On peut placer deux hexagones opposés par le sommet sur le PSH même pour des valeurs assez importantes de \(p\), en tout cas loin du minimum. On notera aussi que la longitude du centre est plus proche de la frontière de la feuille principale que la configuration ci-dessus. La latitude du centre est aussi plus proche de l’origine du repère.
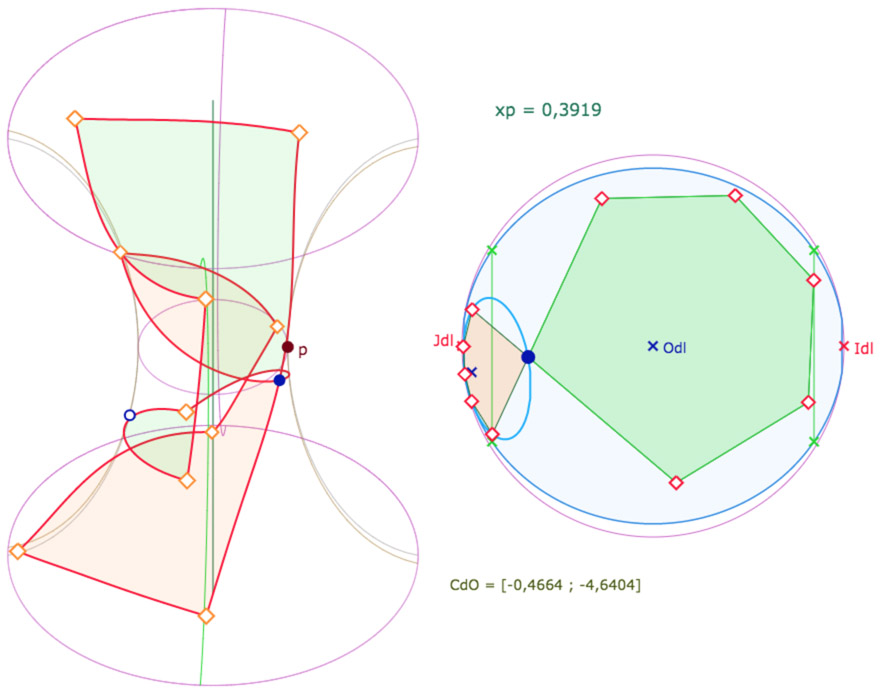
Deux vues de cette configuration
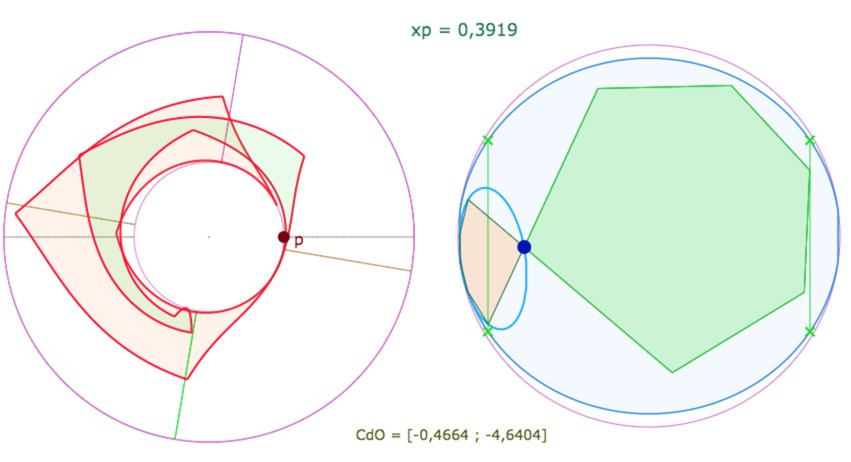
Les 4 hexagones orthogonaux simultanément sur la pseudosphère
Pour mieux voir ce qu’il se passe, on présente d’abord chaque hexagone séparément, vu de dessus.

Cela permet de voir que chacun d’eux fait presque un tour de la PSH, en particulier les deux premiers.
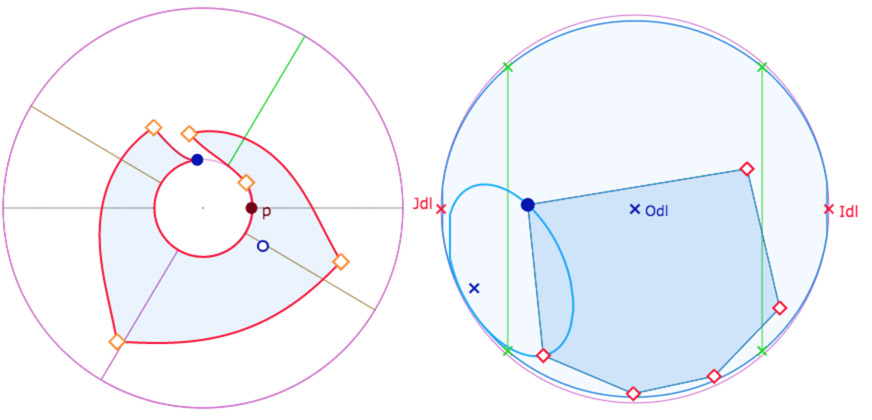
On notera que les deux premiers hexagones coupent une frontière verte de la feuille principale mais que ce n’est pas la même.
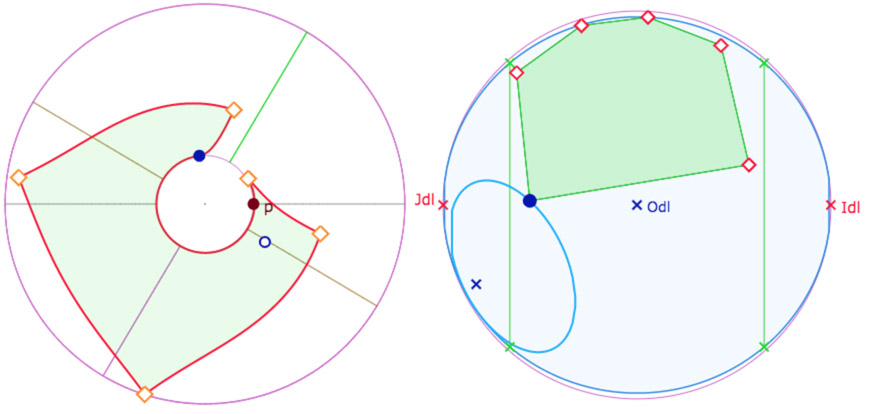
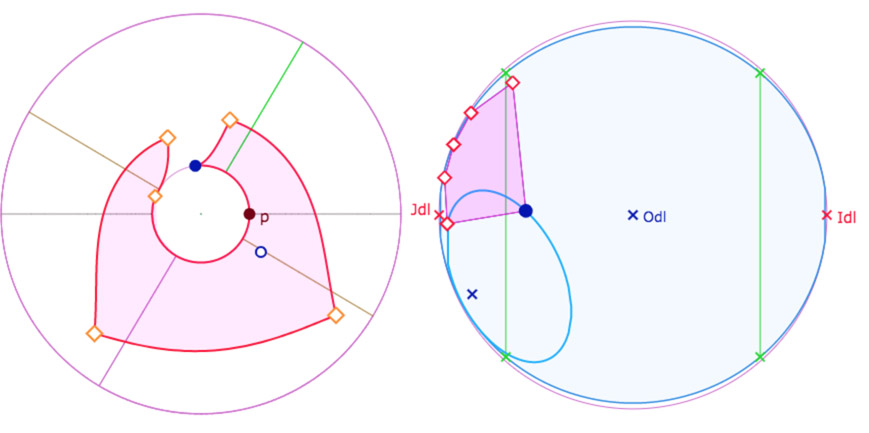
Seul l’hexagone vert – dans cette configuration – est entièrement dans la feuille principale
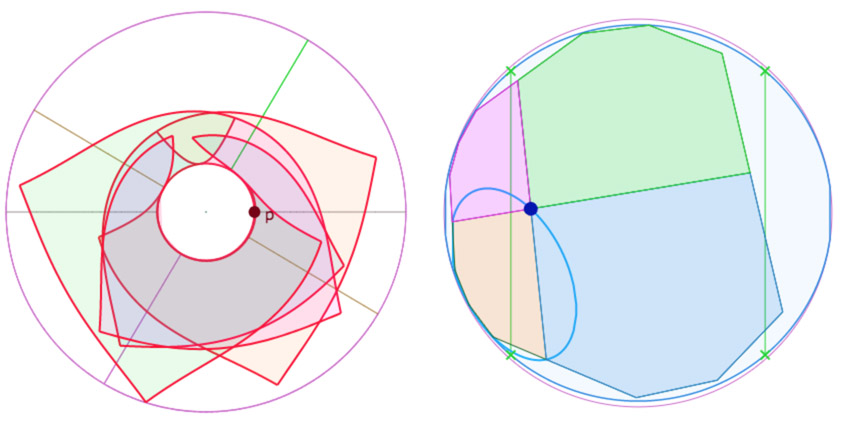
Les quatre hexagones simultanément, d’abord en vue de dessus
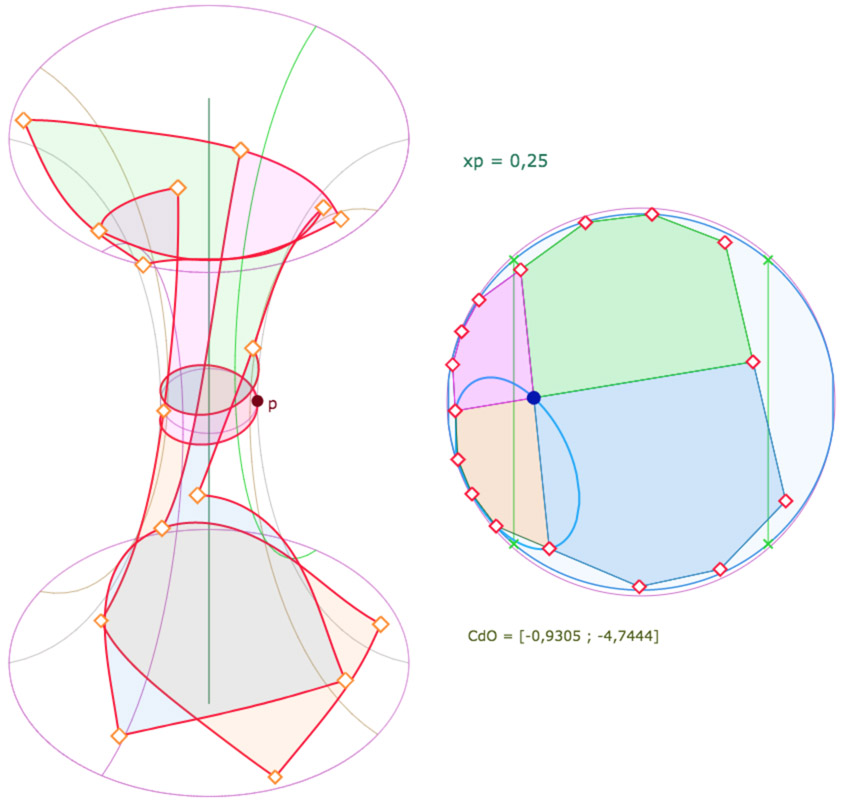
Et en vue de face … Ici p est réglé sur le minimum possible du paramètre
Manipulation de la figure
Comme pour la figure précédente, celle-ci aussi est trop haute pour être ouverte dans une iframe. On l’ouvrira donc directement dans un nouvel onglet.
Les mêmes consignes que les pages précédentes s’appliquent : si on manipule beaucoup la surface elle-même, penser à afficher parfois le repère pour vérifer qu’on est dans un repère direct.
Être en mode consultation (aucun outil sélectionné) pour changer l’orientation ou tourner la pseudosphère à la souris ou au doigt.