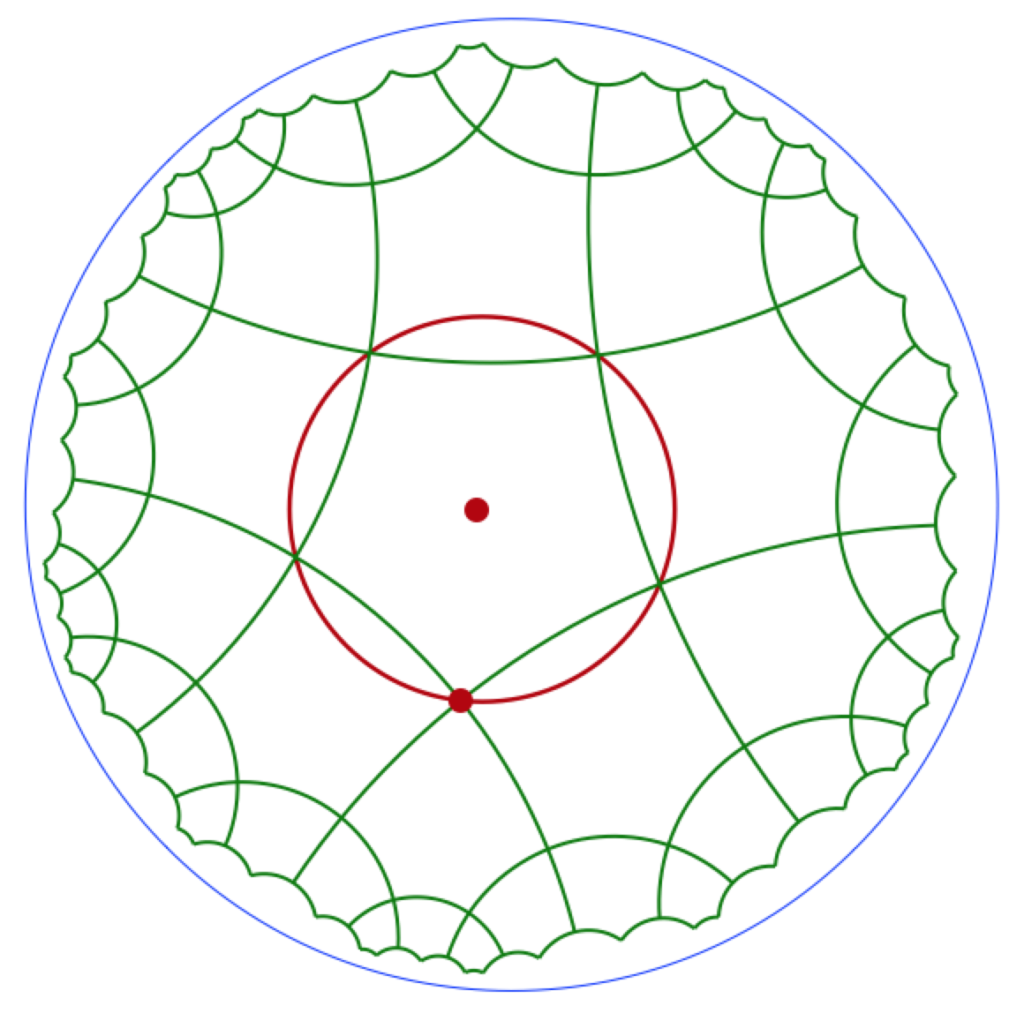
En géométrie hyperbolique la somme des angles d’un triangle n’est pas une constante comme en géométrie euclidienne, elle est seulement inférieure à \(\pi\). Il en résulte une grande diversité des figures.
Un polygone régulier est un polygone qui a tous ses côtés égaux et tous ses angles égaux. Comme dans le cas euclidien, un polygone régulier, que l’on choisit convexe, à \(n\) côté s’inscrit dans un cercle avec un angle au centre \(\displaystyle \frac{2\pi}{n}\).
Mais contrairement au cas euclidien, cela ne définit pas l’angle au sommet. Ainsi, il existe des triangles équilatéraux de tout angle strictement inférieur à \(\displaystyle \frac{\pi}{3}\) et une infinité de carré de tout angle inférieur à \(\displaystyle \frac{\pi}{2}\).
Autrement dit, on peut mettre – théoriquement dans un premier temps – \(k\) triangles équilatéraux autour d’un point pour tout \(k>6\). En itérant ceci à chaque sommet, on aboutit à un pavage de triangles équilatéraux égaux. On nommera \(P(3,k)\) un tel pavage, avec \(k\) triangles par sommets.
De même pour les carrés, on ne fera pas de pavages de carrés à angle droit : on a déjà vu qu’il n’existe pas de rectangle en géométrie hyperbolique et donc pas de carré à angle droit. Mais par contre pour tout \(k>4\), il existe (toujours théoriquement) un pavage de carrés avec \(k\) carrés par sommets : il existe des pavages \(P(4,k)\) à partir de \(k=5\).
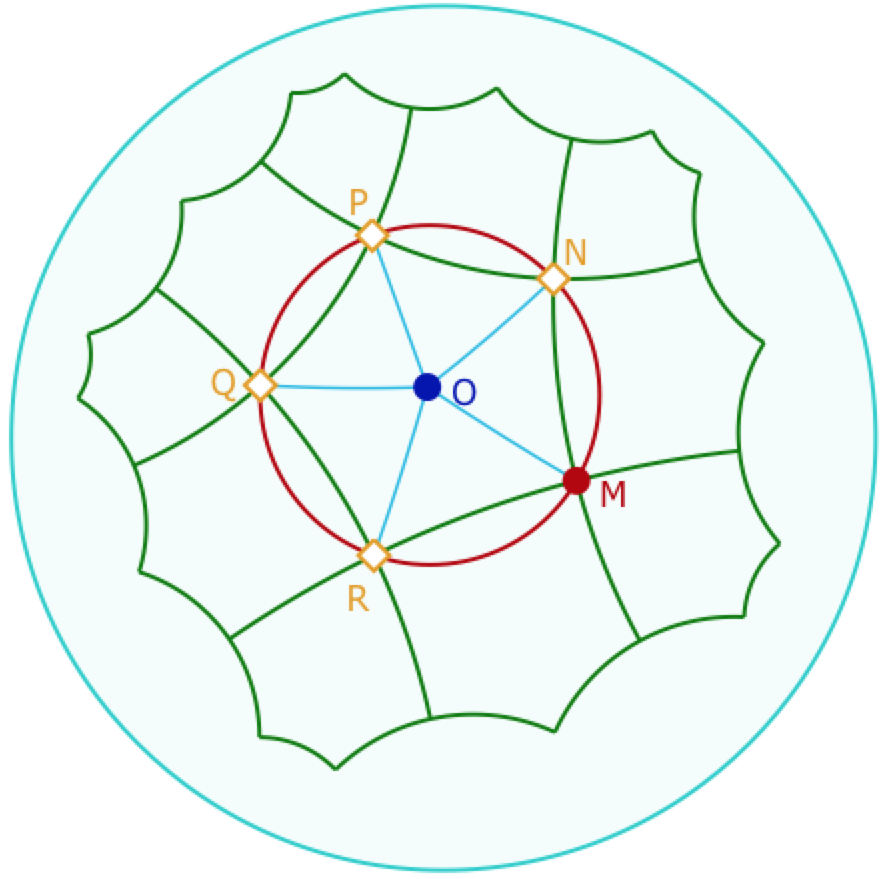
D’une manière générale, un polygone à \(n\) côtés a son angle au centre (l’angle \(\angle MON\) ci-contre avec \(n=5\)) égal à \(\displaystyle \frac{2\pi}{n}\).
Si on place \(k\) tels polygones en chaque sommet (ci- contre \(k=4\)), l’angle au sommet est \(\displaystyle \frac{2\pi}{k}\).
Comme les triangles \(OMN\) et \(NOP\) sont isocèles, l’angle d’un triangle élémentaire \(OMN\) a ses angles à la base de \(\displaystyle \frac{\pi}{k}\).
La somme des angles du triangle inférieure à \(\pi\) s’écrit alors \(\displaystyle \frac{2\pi}{n}+\frac{2\pi}{k}<\pi\). et donc
Le pavage P(n, k) existe si et seulement si \(\displaystyle \frac{1}{n}+\frac{1}{k}<\frac{1}{2}\)
Existe, mais qu’en est-il de sa constructibilité ?
Les résultats de Bolyaï
Dés 1829 (manuscrit publié seulement en 1832), donc bien avant qu’on en connaisse un premier modèle euclidien, Bolyaï avait étudié avec beaucoup de minutie la question de la constructibilité des longueurs en général. Cela constitue environ le tiers de son mémoire qui fonde – avec celui de Lobachevsky – l’existence de la géométrie hyperbolique. Par un long processus, qui utilise que la géométrie de l’horisphère est euclidienne, il a montré que la longueur r est hyperboliquement constructible ssi sh(r) est euclidiennement constructible (équivalent à \(ch(r)\) constructible).
La fin de l’article de Bolyaï montre que la quadrature du cercle est possible – à la règle et au compas bien entendu – en géométrie hyperbolique. L’aire d’un triangle est égale au défaut d’angle à \(\pi\), soit \(\pi-\widehat{A}-\widehat{B}-\widehat{C}\). Bolyaï a ainsi montré qu’un carré d’aire \(\pi\) – c’est-à-dire un carré d’angle au sommet \(\displaystyle \frac{\pi}{4}\) est constructible. Pour cela, il a explicitement calculé le rayon du cercle circonscrit au carré \(x\) qui vérifie la relation \(ch(x)=\displaystyle \frac{\sqrt{2+\sqrt{2}}}{\sqrt{2-\sqrt{2}}}\), ce qui prouve qu’il est constructible. C’est la valeur calculée par BolyaÏ. On notera qu’elle se simplifie en \(ch(x)=1+\sqrt{2}\). Il avait d’abord montré qu’un cercle d’aire \(\pi\) est aussi constructible car cela revient, par une très subtile transformation d’un arc d’horicycle en angle, juste à construire un angle de \(\displaystyle \frac{\pi}{4}\).
La démarche de Bolyaï est illustrée dans deux articles de blog, tout d’abord celui-ci – qui fonde la géométrie hyperbolique – et ensuite celui-là qui traite de la constructibilité des segments et de la quadrature du cercle.
Le pavage P(4, 8) de carrés d’angles à 45° et donc de carrés d’aire \(\pi\). On peut déplacer \(O\) pendant l’animation.
Cette figure est surtout un hommage au travail précurseur de Bolyaï sur la constructibilité.
Exploration des pavages P(3, k) pour k=7 et 8
A partir de deux points \(A\) et \(B\) on construit des triangles équilatéraux autour de ces points puis on déplace un des deux points pour fermer les pavages \(P(3, 7)\) et \(P(3, 8)\) comme ceci :
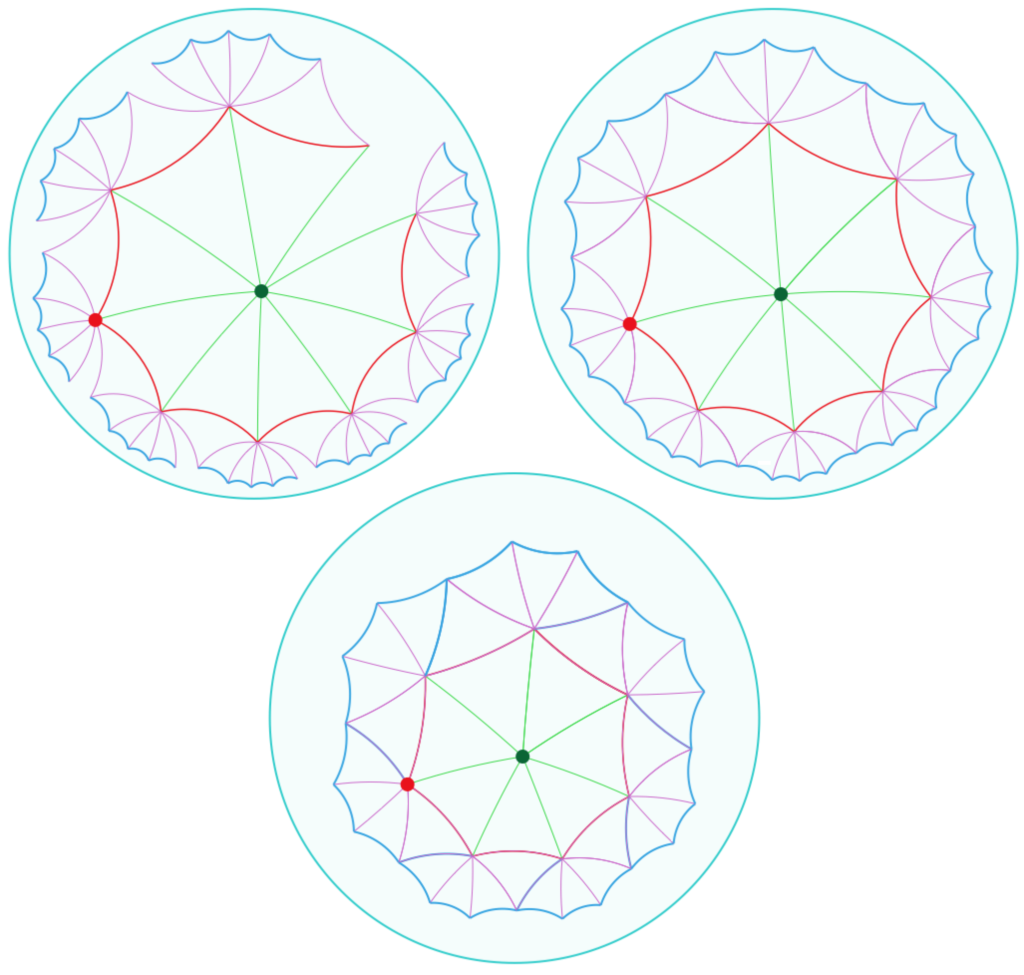
Déplacer un des deux points de base pour faire coïncider les extrémités de P(3,8) et pousser plus loin pour aller jusqu’à P(3,7).
Simulation des P(4,k) (k=5 et k=6)
à partir d’un carré de diagonale donnée [AC]
Pour changer d’approche, on choisi de partir d’un carré de diagonale donnée, \([AC]\), en manipulation directe.
Carré direct de diagonale donnée.
Une premier objectif qui peut être abordé est celui de la construction d’un carré direct ABCD qui résiste à la manipulation des points \(A\) et \(C\). Cette question est posée car, a priori, quand le cercle euclidien support de la diagonale [\([BD]\) change d’orientation les points sont inversés.
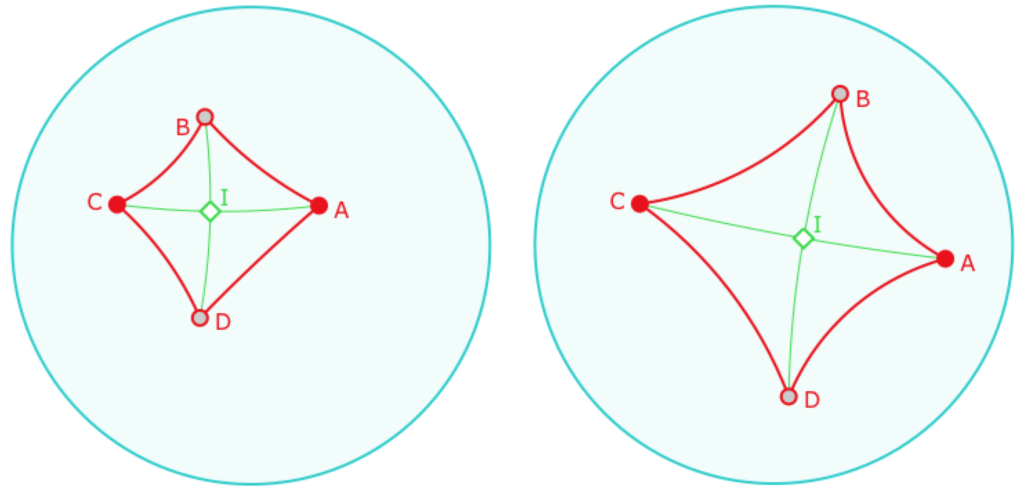
Bien entendu, ce n’est pas une question hyperbolique. C’est une question de représentation dynamique dans un modèle. Nous avons choisi de ne pas mélanger cette introduction aux géométries non euclidiennes avec un catalogue des techniques nécessaires à la réalisation des figures dynamiques comme celle-ci. Il s’agit juste de signaler ici au lecteur que s’il essaie, tout logiciel de géométrie dynamique confondu, c’est assez logique que cela ne fonctionne pas spontanément, un travail spécifique, sur les intersections est nécessaire. Typiquement, il faut construire une macro hyperbolique «intersection droite-cercle».
D’un autre côté, dans ce cas précis, cela peut ne pas être important, il faut juste savoir que, même si on ne nomme pas les points, la figure pouvant basculer sur son symétrique par rapport à \((AC)\) en déplaçant les points \(A\) ou \(C\), on perçoit juste un scintillement de la figure. C’est pour éviter ce scintillement que l’on a fait le choix de construire un carré direct dans toutes les configurations.
Une fois le carré construit, on réalise son symétrique par rapport à chaque côté, puis on poursuit sur les carrés construits, de façon à obtenir 6 carrés autour de chaque sommet.
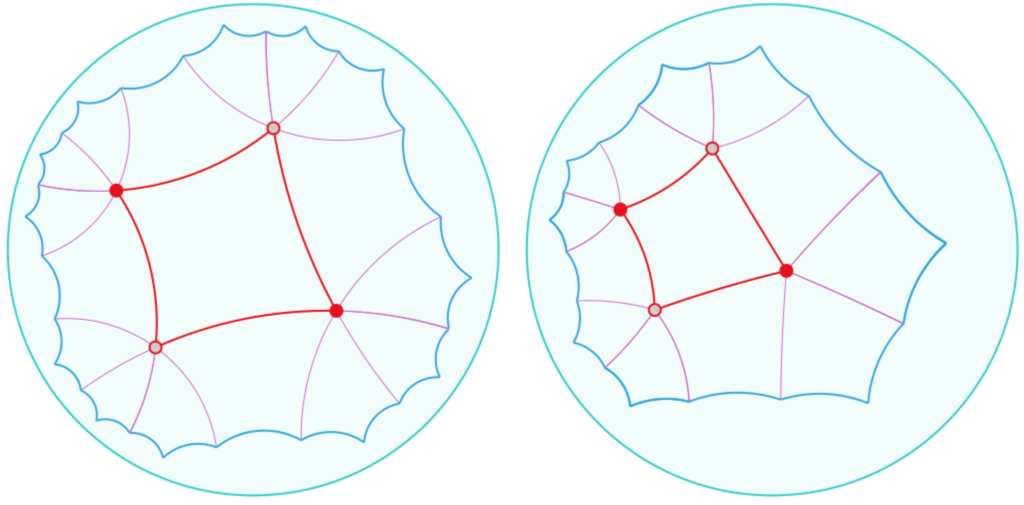
à gauche, la génération 1 d’un pavage de carré d’angles de 60° à chaque sommet, à droite, le cas de carrés d’angles de \(\displaystyle \frac{2\pi}{5}\).
Dans la figure suivante, vous pouvez agir sur les deux points \(A\) et \(C\), en gras pour réaliser, expérimentalement s’entend, les deux pavages \(P(4,5)\) et \(P(4,6)\) .
Exemple des pavages hyperboliques
P(4,5) et P(5,4) – Génération 1
Le cercle de pavage de \(P(4,5)\) est le cercle circonscrit à un carré d’angle 72°. C’est aussi celui d’un pentagone orthogonal (avec 5 angles droits). D’une manière générale, par construction, les pavages P(n,k) et P(k,n) ont même cercle de pavage. Pour lancer la figure dans un nouvel onglet, cliquer sur l’image.
On peut déplacer le centre du cercle \(O\), et passer de l’un à l’autre avec le curseur.
Un article de blog est consacré à la construction des cercles de pavages et propose des figures assez complètes de générations 1 de \(P(5,k)\), \(P(6,k)\) et P \(P(8,k)\) pour plusieurs valeurs de \(k\). Voici la dernière figure de l’article.
Penser à déplacer le centre du cercle pendant l’animation (et changer le pavage)
Préférer ouvrir cette figure dans un nouvel onglet
Autour du pavage P(7,3)
On quitte ici le domaine des pavages « constructibles à la règle et au compas ». Pour le réaliser on utilise une macro « Cercle par centre et ch(r) » comme présentée dans cet article sur les macros du disque de Poincaré.
Dans cette même page, la construction de ce pavage est détaillée avec des figures intermédiaires à télécharger pour faire soi-même, soit toute la figure, soit les parties finales. En voici deux illustrations :
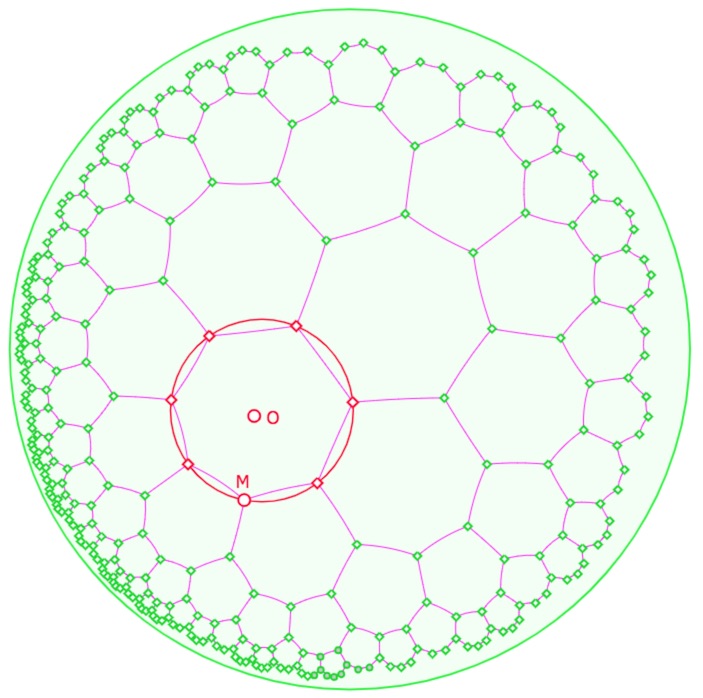
Lancer cette figure dans un nouvel onglet (\(M\) est animé, déplacer \(O\) pendant l’animation).
Et celle-ci, plus particulière où le triangle de base est partagé en deux triangles rectangles pour des raisons expliquées dans la page.

Lancer cette figure dans un nouvel onglet.
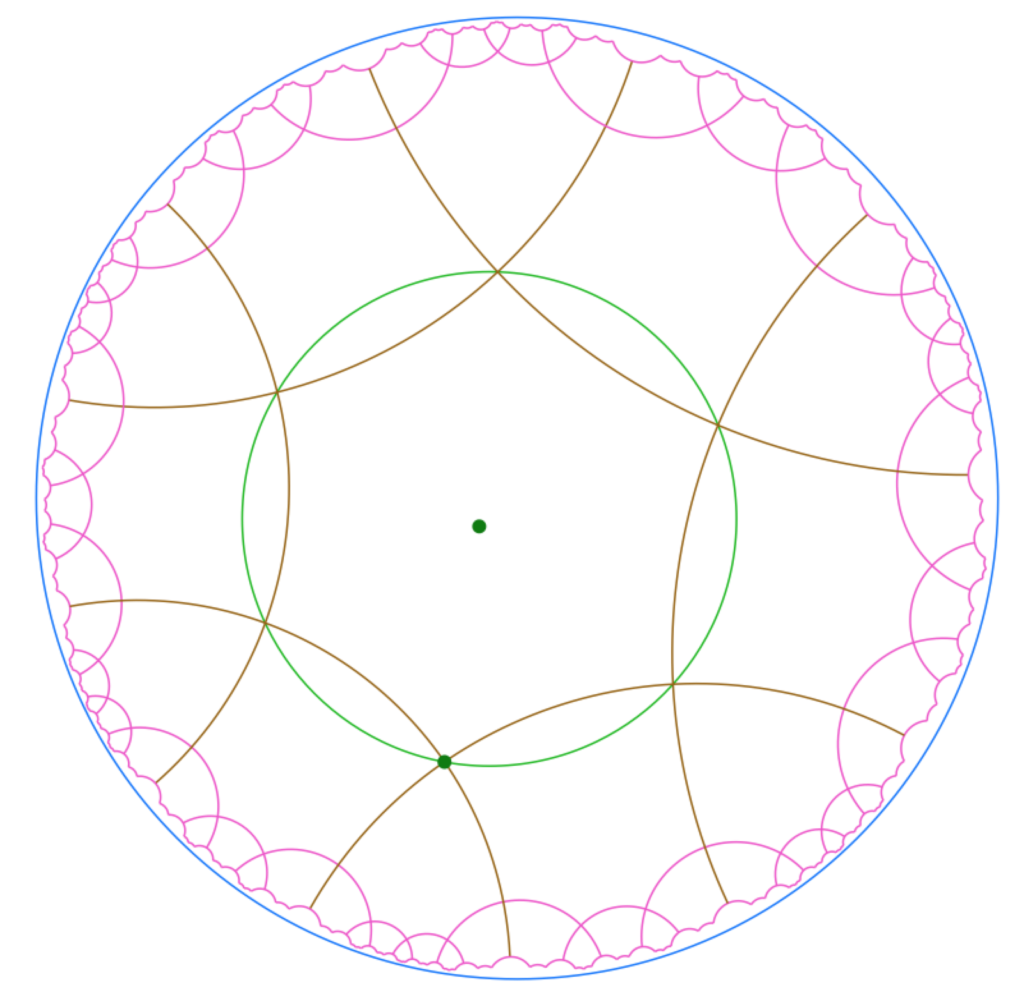
P(5,4) et P(6,4) – Génération 2
(avec des pentagones ou des hexagones orthogonaux)
Ces deux figures sont plus longues à ouvrir (jusqu’à 30 s) on les lance dans des pages à part en cliquant sur les illustrations ci-dessous. On peut déplacer le centre du cercle pendant l’animation.
Pavage (génération 2) de pentagones orthogonaux.
Il sont d’aire \(3\pi – 5 \displaystyle \frac{\pi}{2} = \frac{\pi}{2}\)
d’aire \(\pi\), on a donc aussi une « hexogature » de \(\pi\).
Autre type de pavages réalisés
ailleurs dans le site
1. les pavages non réguliers orthogonaux. (générations 1 et 2 comme ci-dessous)
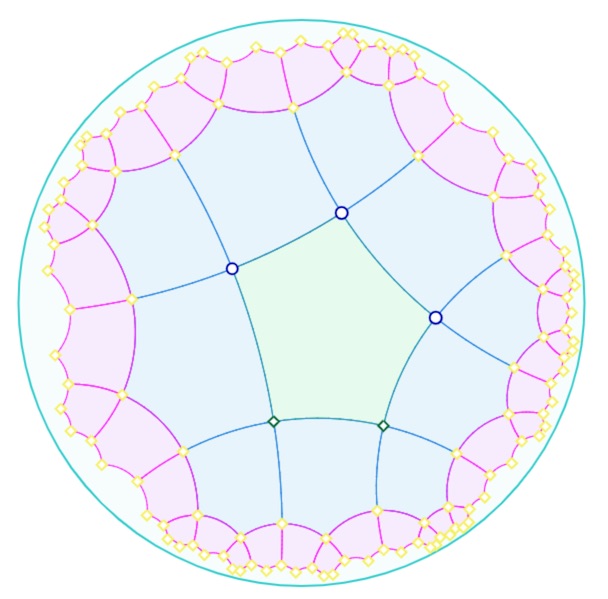
Pavage non régulier PnR(5,4)
2. Pavages réguliers construits sur des horicycles