Construction d’une première droite de la PSH
En dehors des méridiens, toujours d’équation \(\theta=Cst\), les autres géodésiques de la PSH sont déterminées (avec \(k\) et \(c\) deux constantes) par la relation : \(\theta =\displaystyle \frac{1}{p}th^{-1}\left(\displaystyle \frac{c \, sh(u)}{\sqrt{p^2ch^2(u)-c^2}}\right)+k\).
Pour une construction intrinsèque, il faudrait trouver \(k\) et \(c\) à partir de deux points \(A(u_A, \theta_A)\) et \(B(u_B, \theta_B)\), ce qui n’est pas possible. On travaille donc par conjugaison, et c’est alors très simple à réaliser.
Principe de la construction
On prend un point \(M_{ab}\) sur la KB-droite passant par les points image \(A_{kb}\) et \(B_{kb}\) et plus précisément, sur la partie à l’intérieur de la KB-équidistante frontière de l’image de la PSH. On renvoie alors ce point sur la pseudosphère hyperbolique en renversant le système de projection de Beltrami : l’abscisse \(x_{M_{ab}}\)détermine la longitude du point sur la PSH par \(\theta_{M_{PSH}} = \displaystyle \frac{1}{p}th^{-1}(x_{M_{ab}})\) et son ordonnée \(y_{M_{ab}}\) permet d’écrire \(u_{M_{PSH}} =th^{-1} \left(y_{M_{ab}}ch(p \theta_{M_{PSH}})\right)\). On termine la droite par le lieu du point courant \(M_{PSH}\). C’est ce que fait la nouvelle macro Drt LesCoef g Odl Mab que l’on voit dans l’illustration suivante.
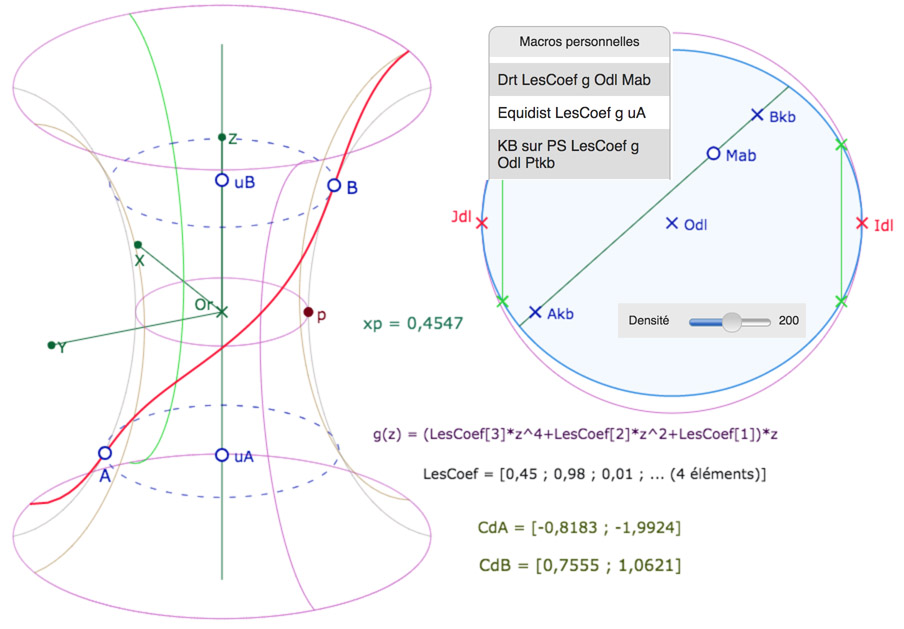
Avant de proposer une figure élémentaire à la manipulation, voyons quelques points particuliers. Tout d’abord mentionnons la seconde nouvelle macro KB sur PS LesCoef g Old Ptkb fait la même chose pour un seul point (il n’y a pas de lieu).
La question des droites multifeuilles
Le cas illustré précédemment est entièrement contenu dans la feuille principale. Dans cette illustration, on montre la densité standard de la droite retenue dans la macro : 200. Pour les simples segments, on la réglera à 50, et parfois même à 20 dans les pavages. On s’intéresse dans ce paragraphe à ce qu’il se passe quand la droite ne se limite pas à la feuille principale. Commençons par une petite valeur de \(p\) car on a vu que cela déploie – dans la représentation sur KB – les deux feuilles autour de la principale. Et c’est important pour disposer de points sur la KB-droite \((A_{kb}B_{kb})\) pour appliquer le lieu de points. Mais pour cela il faut augmenter la densité.
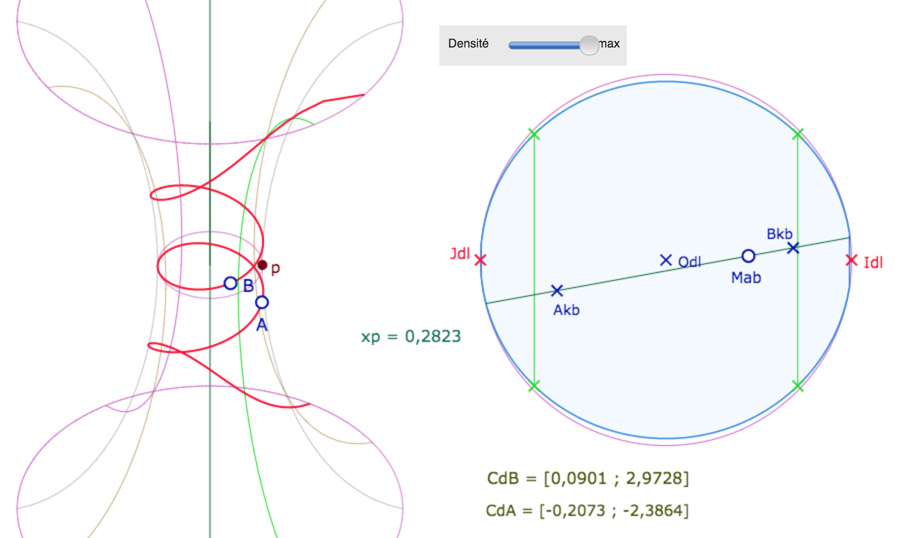
Un exemple de droite déployée sur 3 feuilles de la surface, avec une densité « max » (5000 points).
On voit – et on lit sur sa longitude – que B est très proche du méridien vert, frontière de la feuille principale.
On poursuit en manipulant la figure de la façon suivante. On ne touche pas aux points \(A\) et \(B\) sur la PSH. On augmente seulement la valeur du paramètre \(p\). La courbe s’enroule encore sur 3 feuilles mais il y a beaucoup moins de points disponibles pour le lieu dans les feuilles adjacente à la feuille principale dans KB (d’où un trait un peu trop droit pour le haut de la PSH). Mais regardons aussi un autre phénomène.
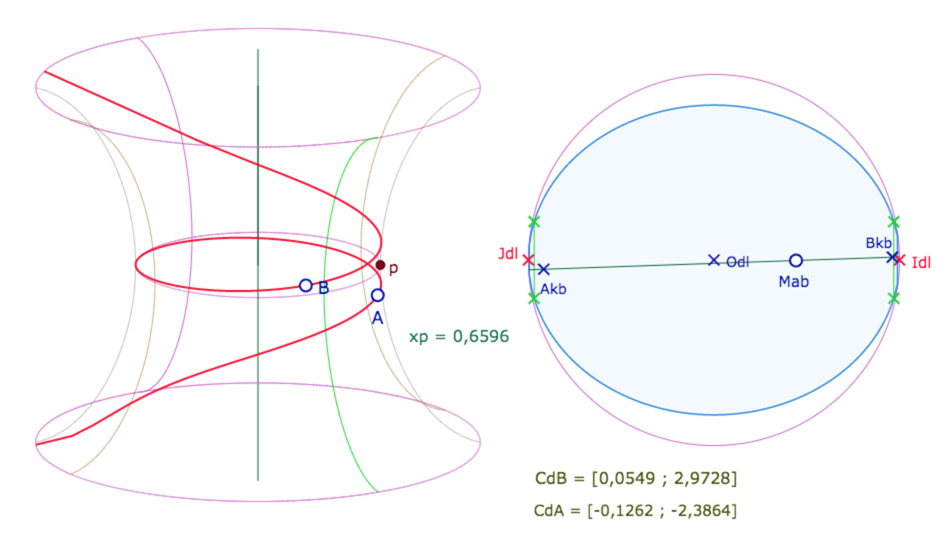
Dans la façon de prendre les latitudes dans ces figures, en changeant la valeur de \(p\), les mêmes points \(A\) et \(B\) conservent bien leurs longitudes mais changent de latitude, et donc la pente euclidienne de la droite \((A_{kb}B)_{kb}\) diminue.
En effet les latitudes \(u_A\) et \(u_B\) sont des points sur objet d’un segment de longueur variable (2AltMax). Or dans les logiciels de géométrie dynamique, l’implémentation des points sur objets est affine (barycentrique) pour que les points sur objet réagissent « naturellement » quand on change les tailles des segments.
Cela peut immédiatement se corriger si, dans une figure, cela devenait nécessaire, en prenant un point sur une droite au lieu d’un segment, mais ce fonctionnement « naturel » relève en général du comportement attendu, car, dans ces constructions, la latitude d’un point est proportionnellement conservée par rapport aux valeurs extrémales possibles.
Manipulation de la figure
Dans cette figure, on a fait le compromis de densifier la droite à 1000 objets (au lieu des 200 de la macro). Idem pour la figure qui s’ouvre dans un autre onglet.
Rappel : l’orientation de la surface se modifie au doigt ou à la souris simplement.
Pour la déplacer en translation il faut faire apparaître le repère et déplacer l’origine.
Préférer ouvrir cette figure (sans restriction) dans un nouvel onglet.
On commence cette exploration sur la PSH par quelques figures usuelles de la géométrie du triangle.
Médianes d’un triangle
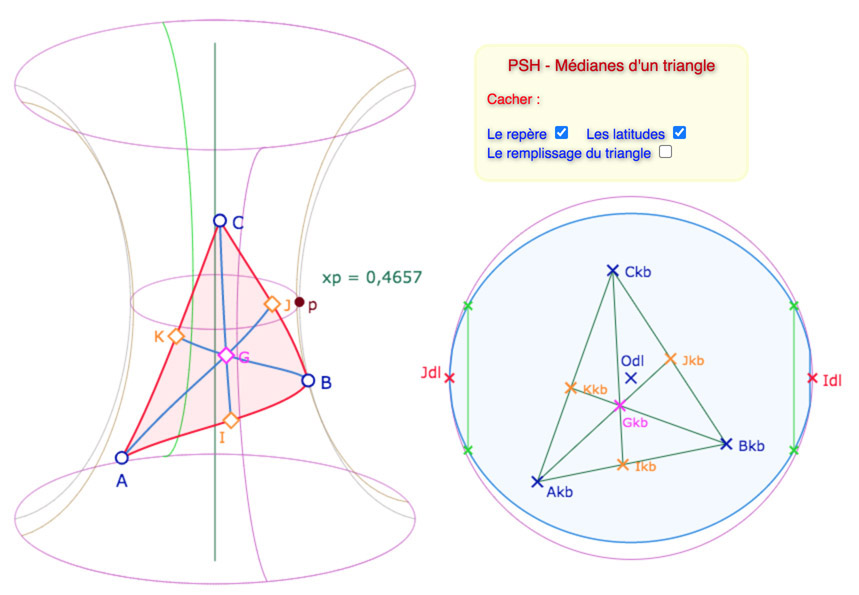
Les médianes sont toujours concourantes en géométrie hyperbolique, donc c’est la version PSH.
Montrer le repère permet de vérifier qu’il est bien direct, parfois, on l’inverse sans vraiment s’en apercevoir.
C’est aussi nécessaire pour déplacer la PSH en translation.
On a choisi d’ajouter un remplissage du triangle. La méthode utilisée est présentée, de manière plus générale, dans ce post de blog. Toutefois, ce remplissage est d’une certaine façon une « illusion d’optique » car le triangle 3D n’est pas convexe, et les algorithmes de remplissage sont fait pour des figures convexes . On peut donc rencontrer des « artefacts » quand on tourne la PSH. Voici un exemple sur un triangle très allongé.
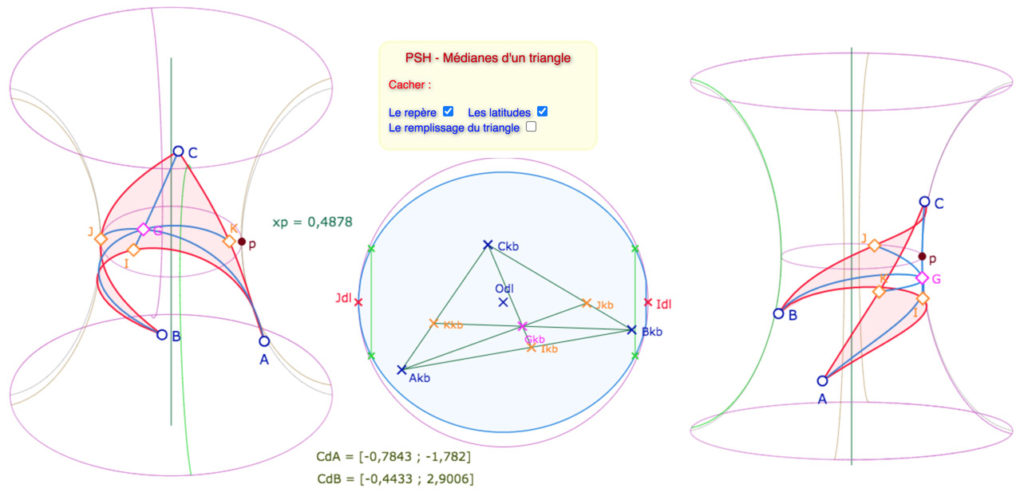
à gauche, même avec une grande amplitude de longitude, le remplissage correspond à ce que l’on attend.
à droite, on a tourné la surface, on voit mieux le fonctionnement.
La figure à manipuler
Il est préférable d’afficher les latitudes (avec les équidistantes support des points) même pour déplacer les sommets du triangle.
C’est bien entendu indispensable pour modifier les latitudes \(u_A, u_B\) ou \(u_C\).
Préférer ouvrir la figure dans un nouvel onglet.
Utilisation des KB-droites FP – exemple des hauteurs
Pour les deux premières pages de ce menu, on choisit de limiter les droites de la surface à sa feuille principale (FP) car cette pseudosphère couvre, dans KB, une grande part du plan hyperbolique et tracer les droites au delà de la feuille principale nécessite de densifier fortement les lieux utilisés.
Pour cela on construit une macro dans KB qui, à partir de deux points, donne toujours le segment correspondant à la feuille principale. C’est juste un jonglage sur des points logiques. Elle s’appelle KB drtFP 2pts 2Fr Cnk dans la liste des macros de KB. On expliquera son utilisation (associée à son nom) dans une page de blog dédiée aux macros de la PSH, car c’est intéressant – et facile – de construire soi-même des figures sur la PSH.
Détail sur la détermination des bornes de FP dans KB

On part de deux points \(M\) et \(M\). On note \(iN\) et \(iM\) les intersections de \((MN)\)avec la conique frontière. Les points \(f_{12}\) et \(f_{34}\) sont les intersections éventuelles avec les images de la feuille principale : l’indice 12 est pour la borne de gauche et 34 pour celle de droite. \(Bg\) et \(Bd\) sont les bornes de gauche et de droite de la KB-droite entière \((MN)\). Puis \(BgFP\) et \(BdFP\) les limites de la restriction à la feuille principale.
Exemple des hauteurs
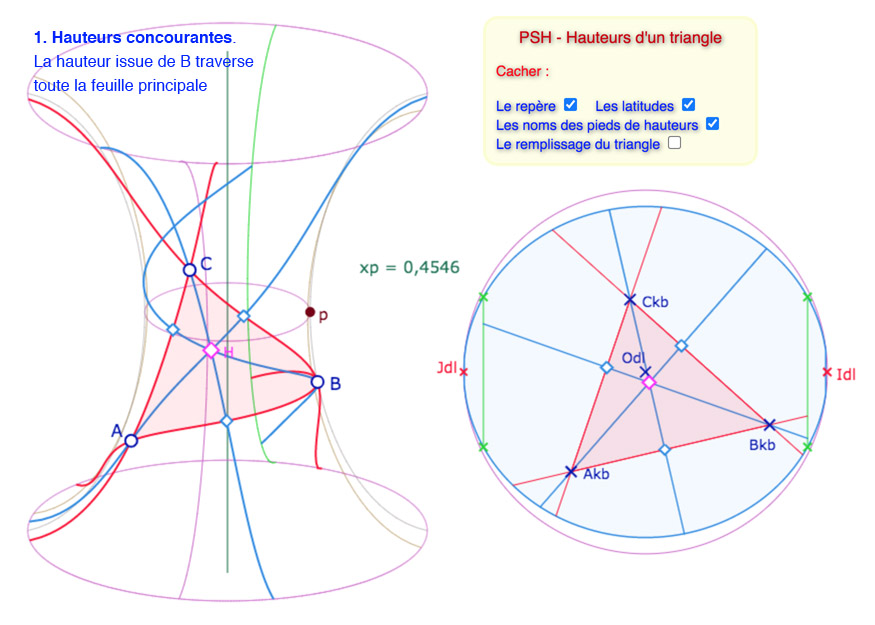
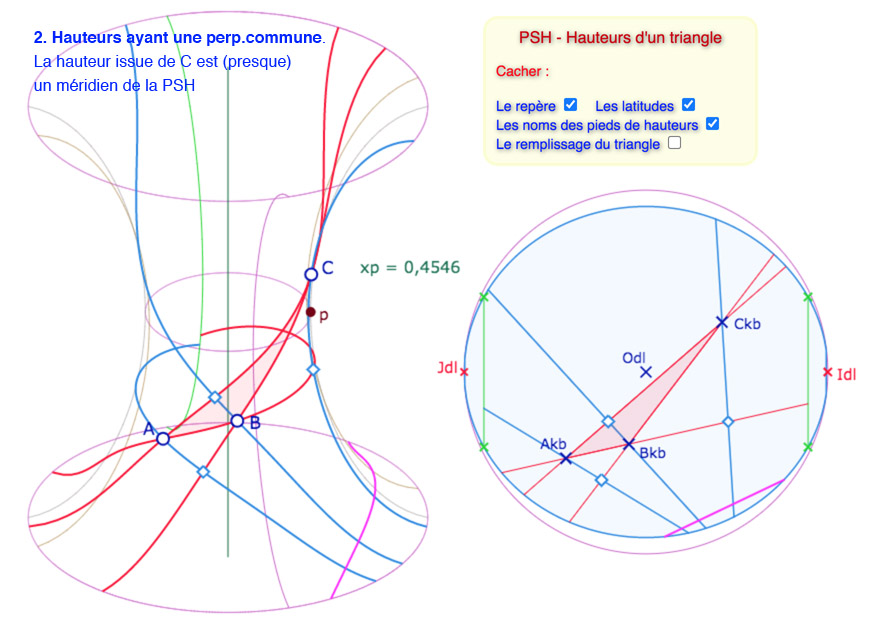
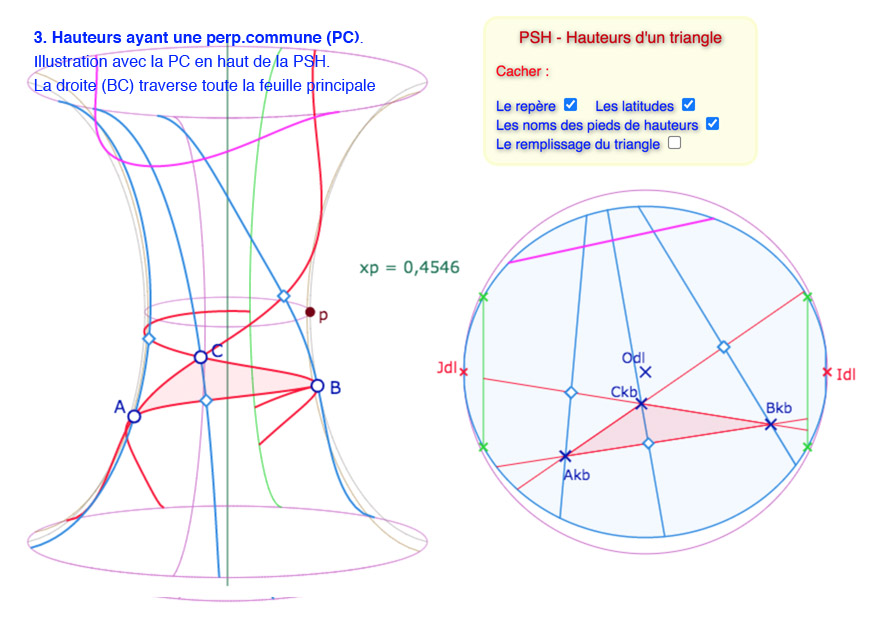
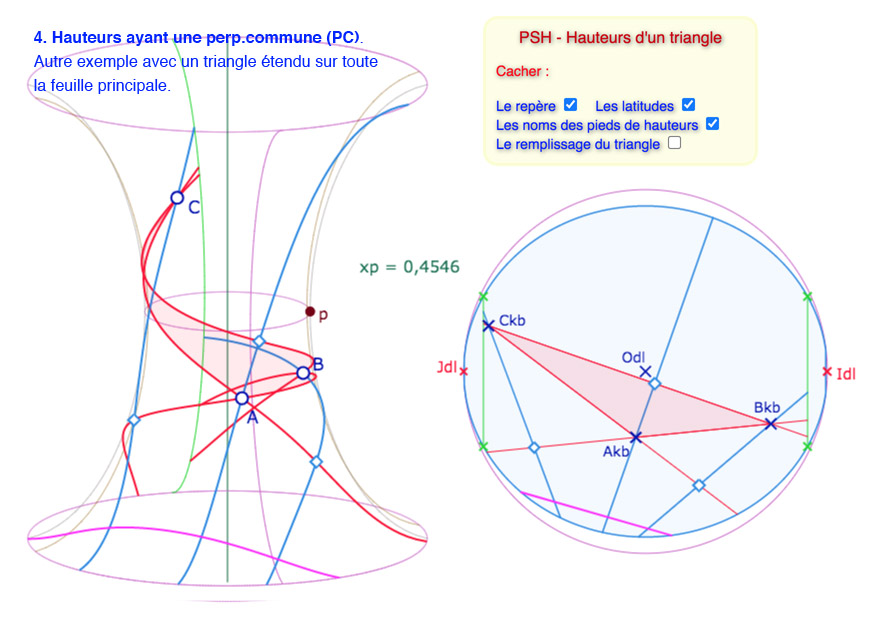
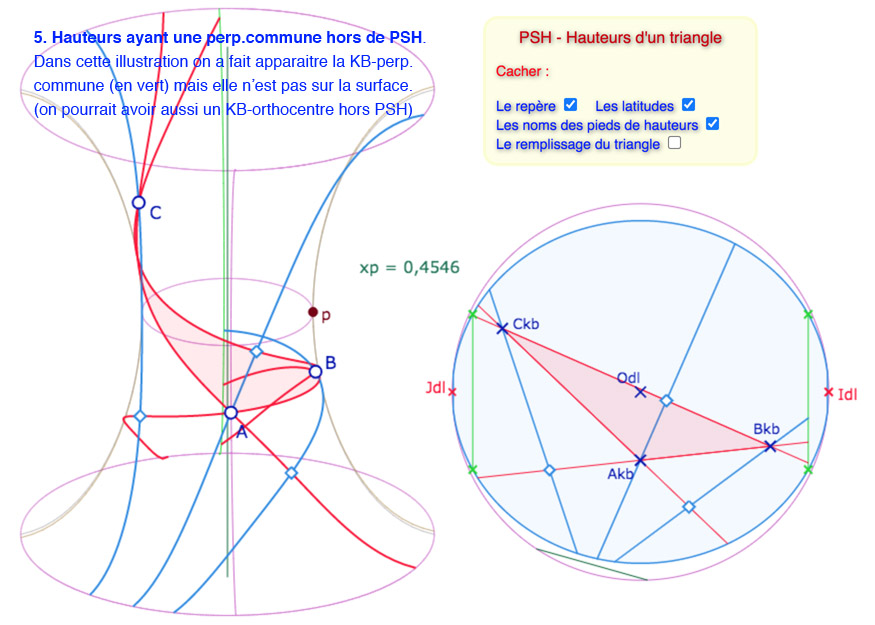
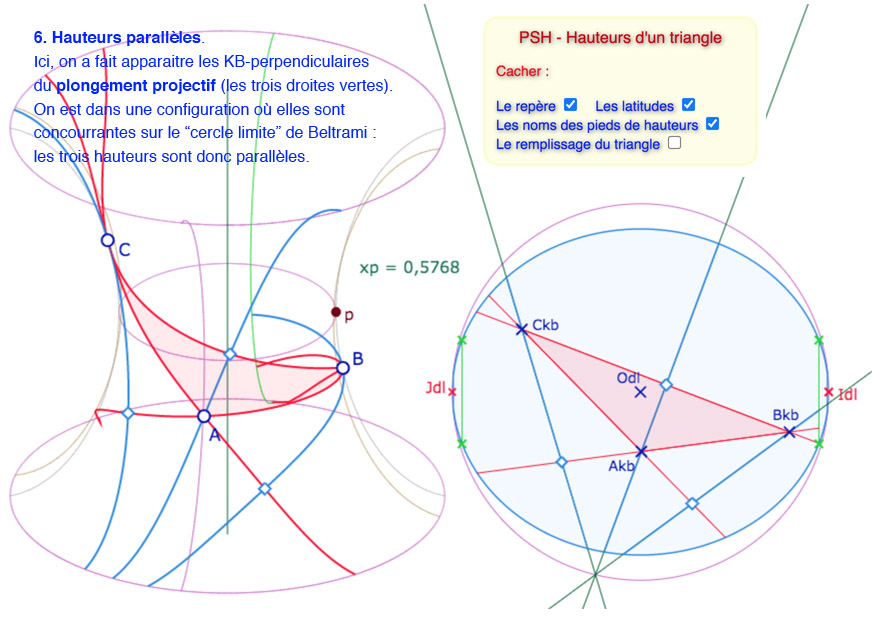
Voici une galerie de 6 illustrations de situations que l’on peut reproduire dans la figure suivante
Sur les six illustrations, les cinq premières ont même valeur de \(p\).
Les droites « compléments hors PSH » des illustrations 5 et 6 ne sont pas disponibles dans la figure suivante.
On peut les faire apparaître dans la figure en ligne (hors restriction) si on a une pratique de l’interface du logiciel.
La figure associée pour manipulation
Ne pas hésiter à modifier tous les paramètres de la figure pour explorer les différentes situations.
Préférer ouvrir cette figure (sans restriction) dans un nouvel onglet
Les médiatrices
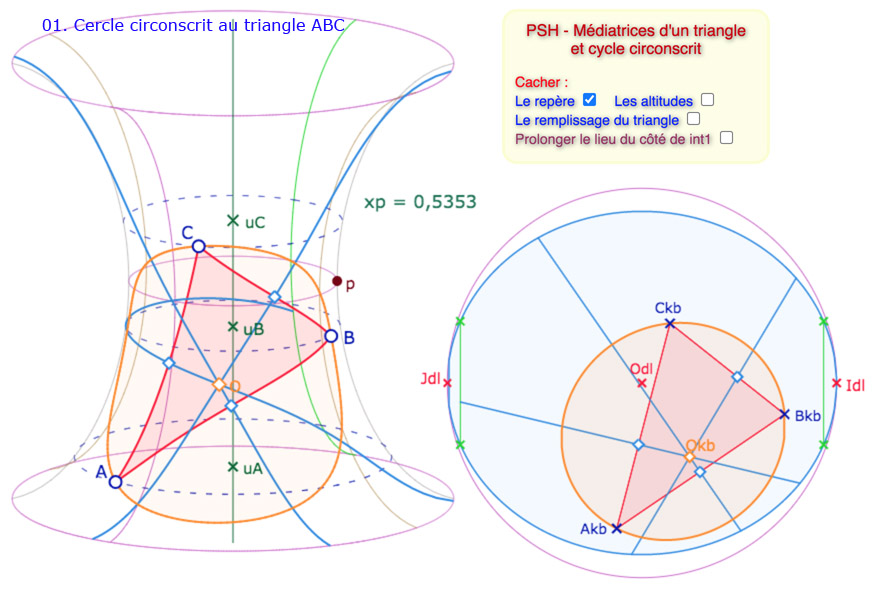
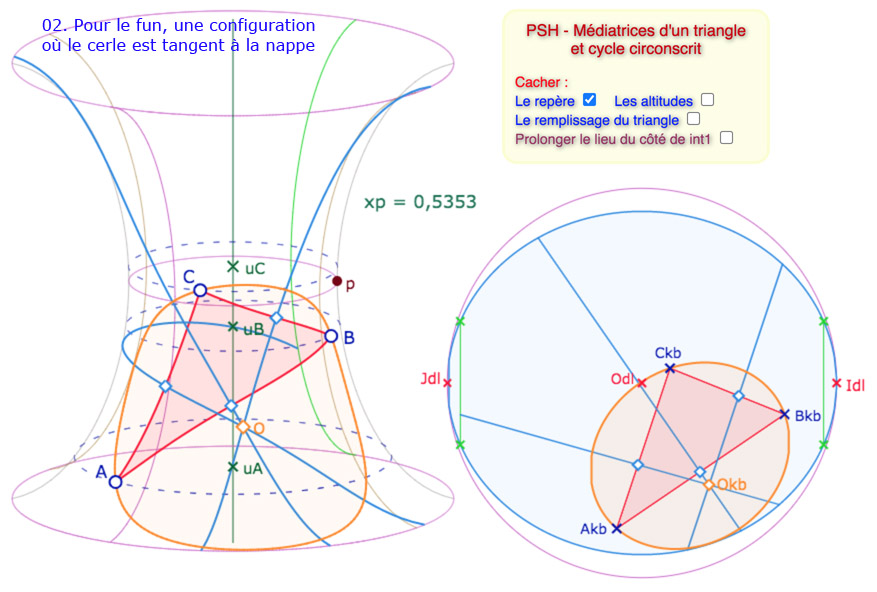
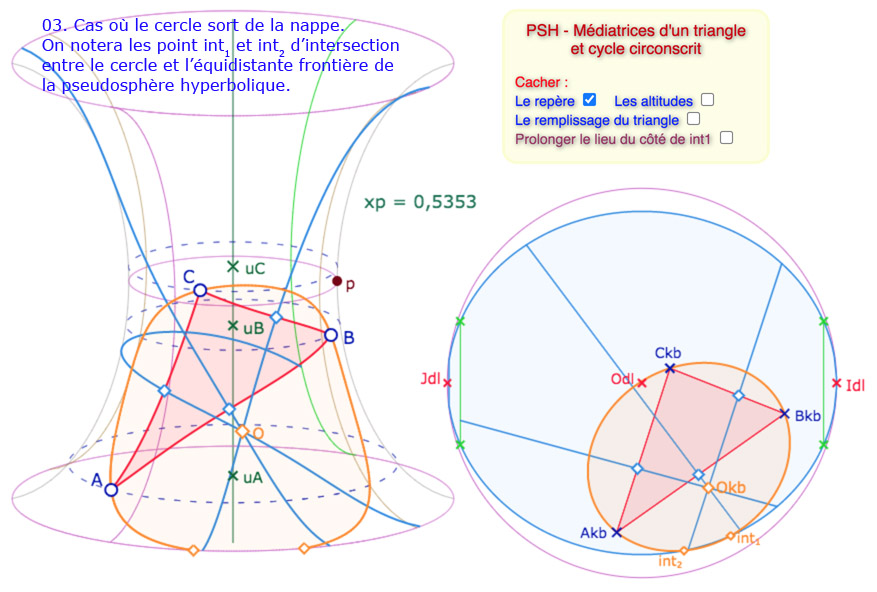
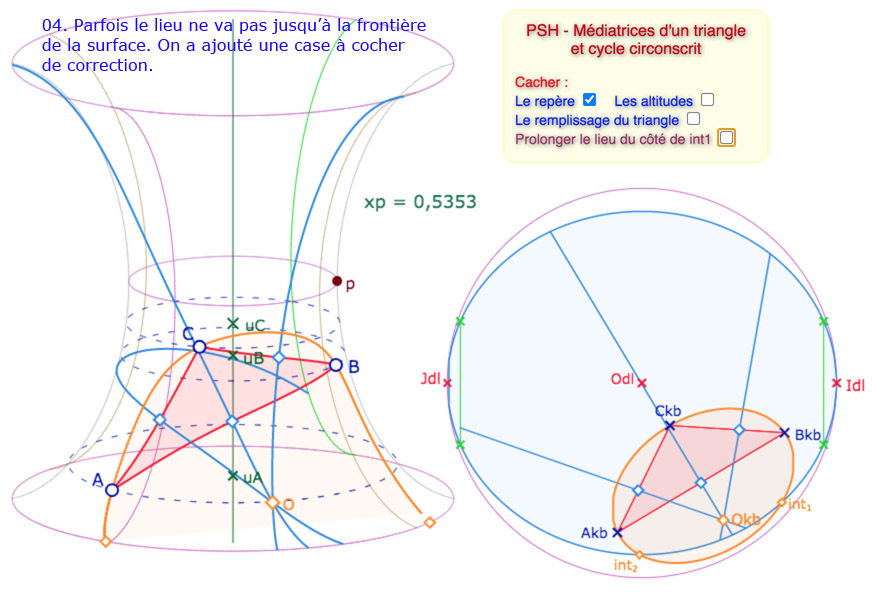
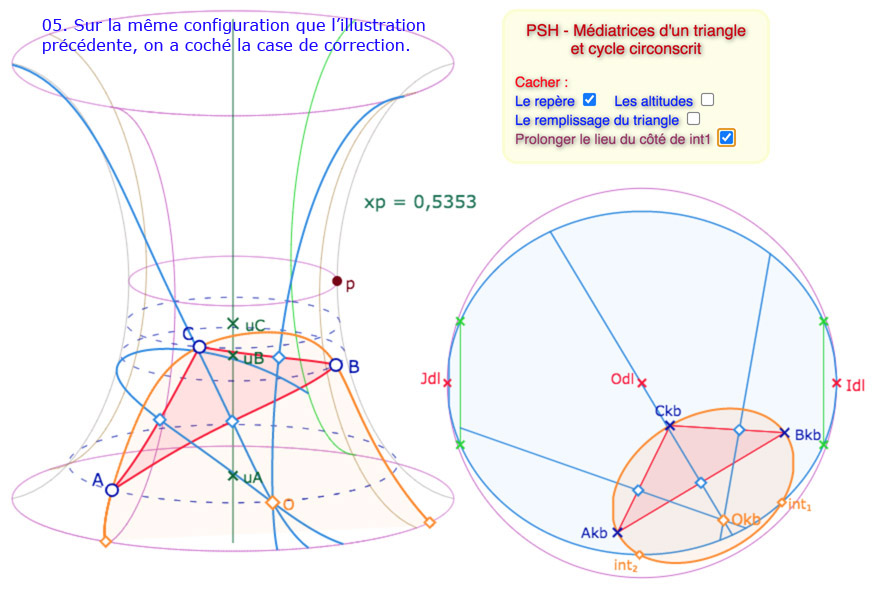
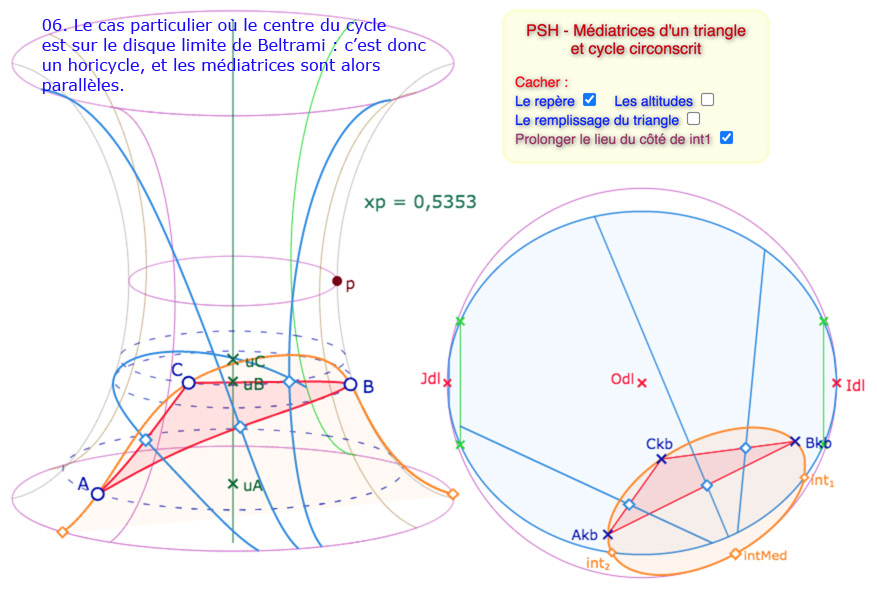
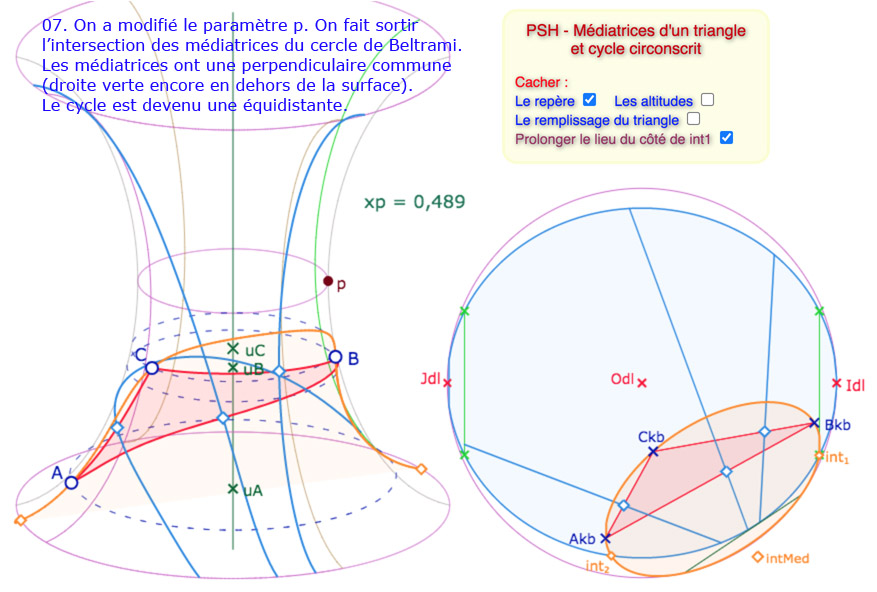
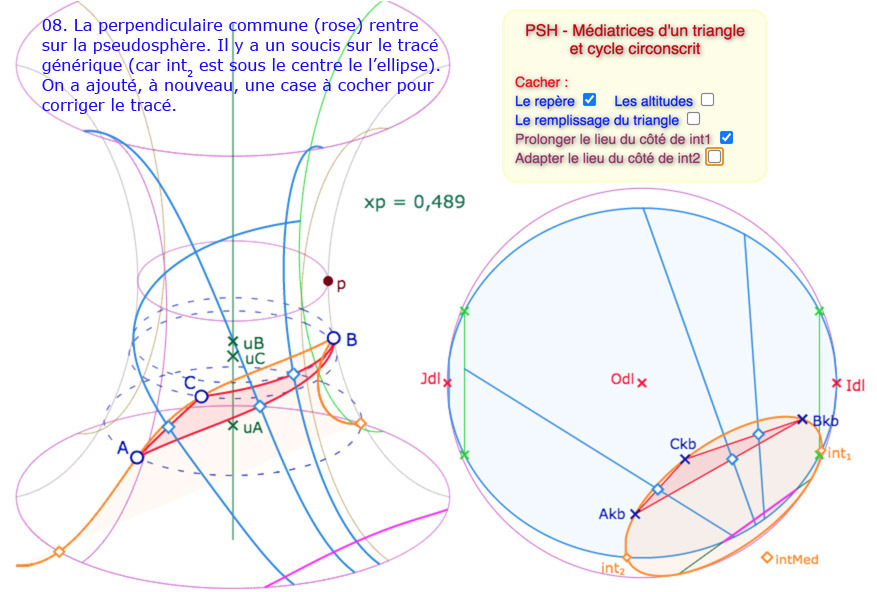
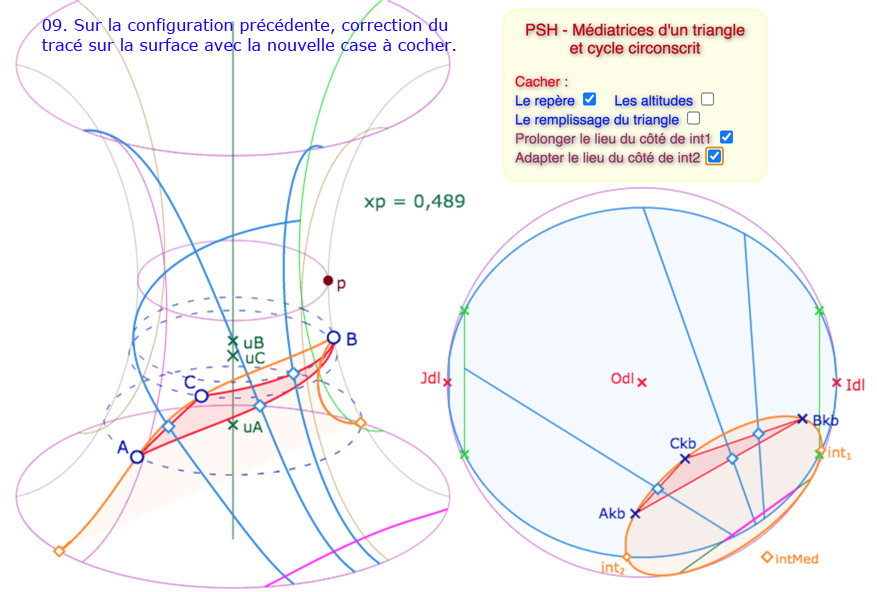
La situation est plus riche si on veut faire apparaître le cycle auquel appartiennent les médiatrices. Voici une galerie de 9 illustrations des principales situations. On a laissé visible la gestion des difficultés, avec des cases à cocher correctives. Bien entendu on aurait pu laisser le tout transparent.
Galerie de 9 illustrations sur le cycle circonscrit à un triangle de la PSH.
La figure correspondante
Dans cette figure, on peut manipuler les sommets du triangle, leurs latitude, le paramètre p et l’orientation de la surface.
On peut reproduire les différentes illustration de la galerie précédente.
Dans cette figure comme sa version sans restriction ci-dessous, seul le dépassement de la surface par le bas de la nappe est traité, la sortie par le haut n’est pas programmé.
Préférer ouvrir cette figure dans un nouvel onglet.
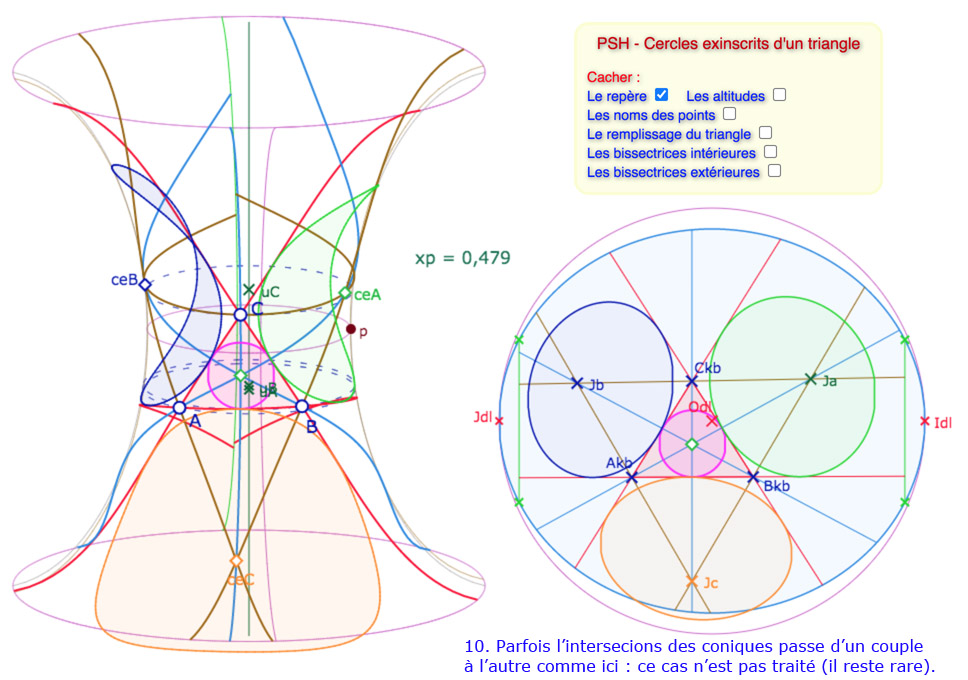
Cercles exinscrits
Vu les deux rustines proposées ci-dessus pour le cycle circonscrit à un triangle, on aura compris qu’il n’est pas toujours simple de programmer l’image sur la pseudosphère d’un arc d’ellipse d’une manière générique. On poursuit néanmoins en réitérant cela deux autres fois, pour avoir les trois cycles exinscrits d’un triangle.
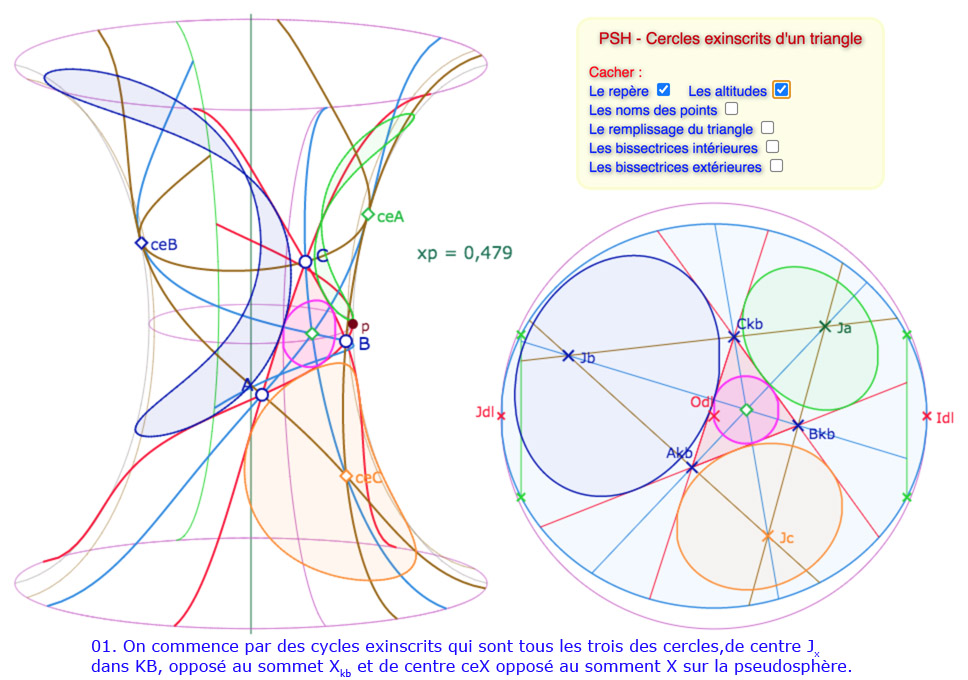
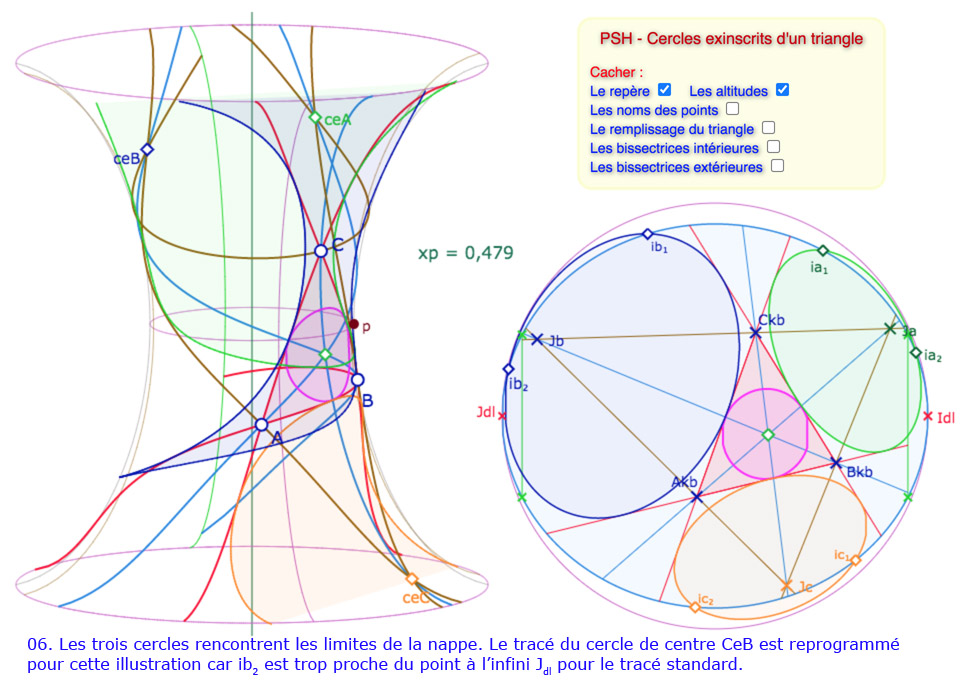
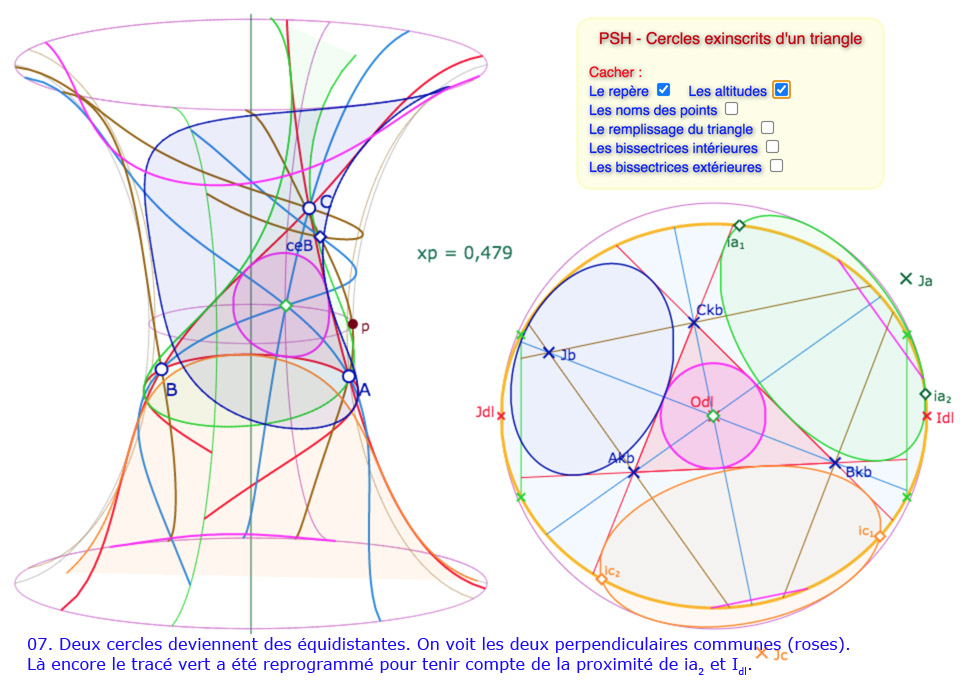
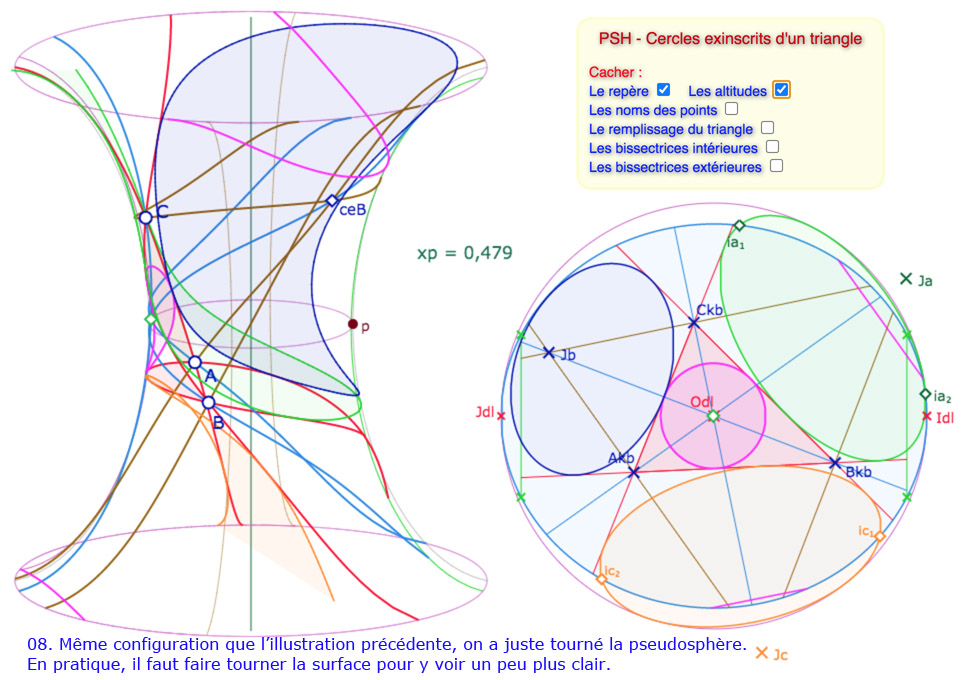
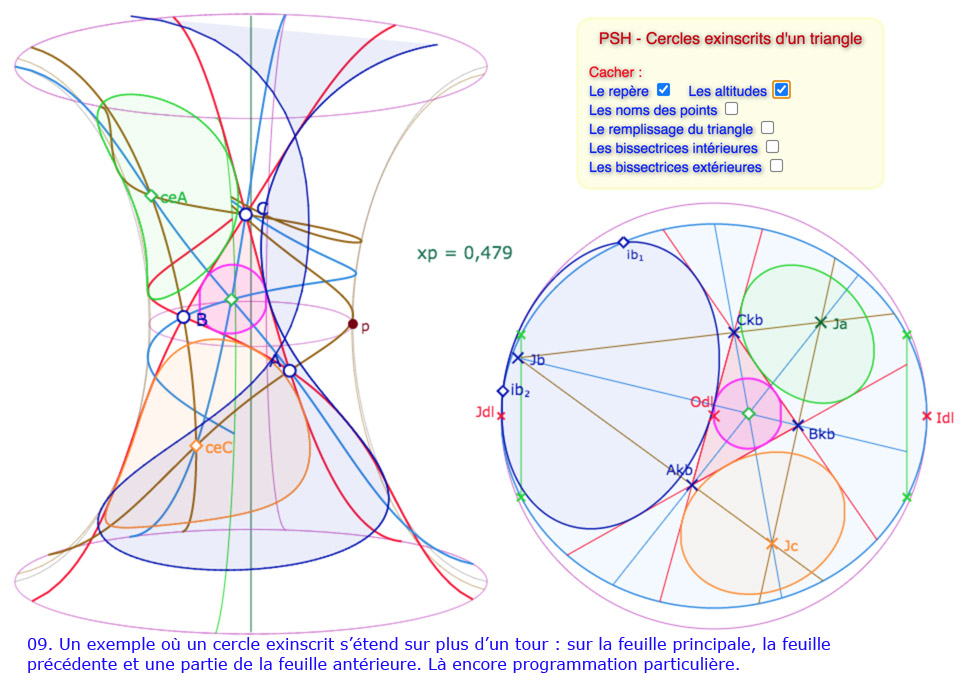
La situation se complique un peu plus dans la mesure où les cycles exinscrits vont sortir de la surface, en des points – dans le disque de Beltrami – qui peuvent être proches des points à l’infini, ce qui signifie un éventuel enroulement de ces cercles sur la surface. Pour ces cas là, il faut un traitement vraiment spécifique, ce qui a été fait pour réaliser les illustrations suivantes mais n’est pas proposé dans la figure générale. Commençons par un petit panorama des situations que l’on peut rencontrer en manipulant la figure.
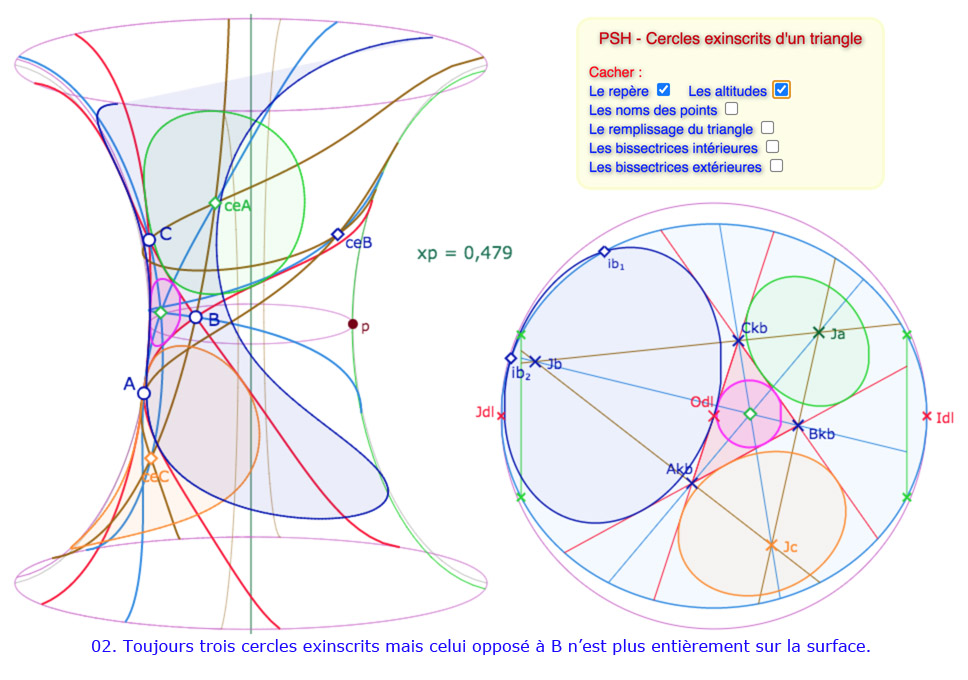
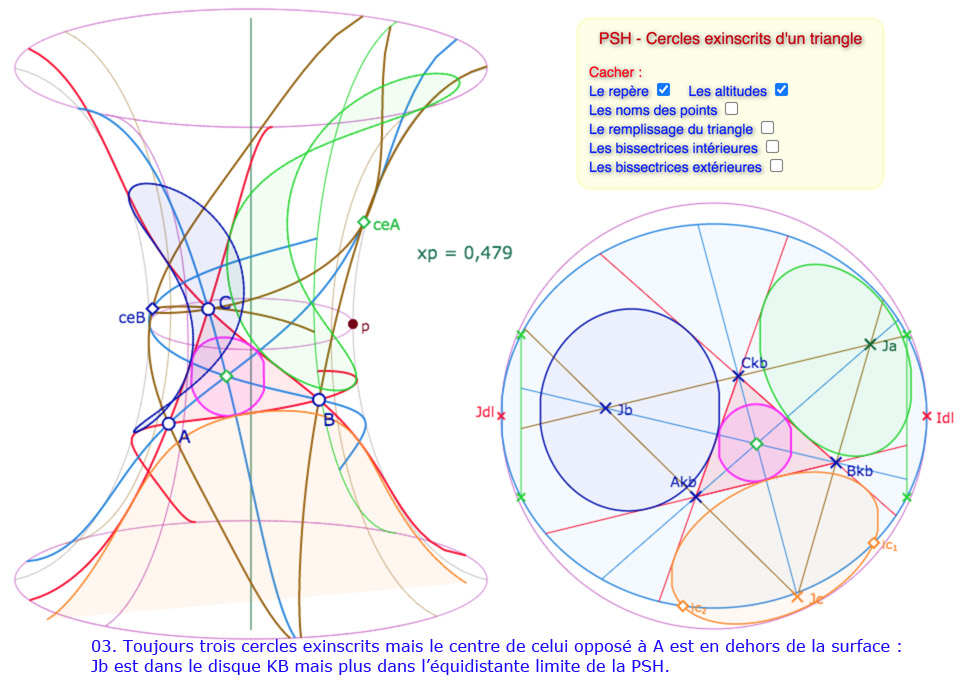
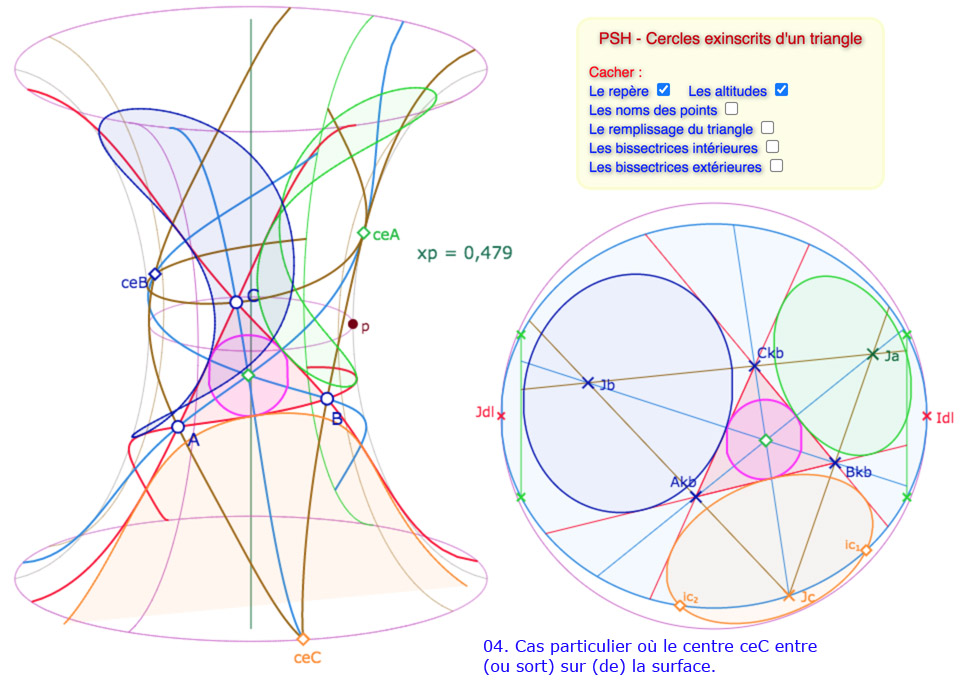
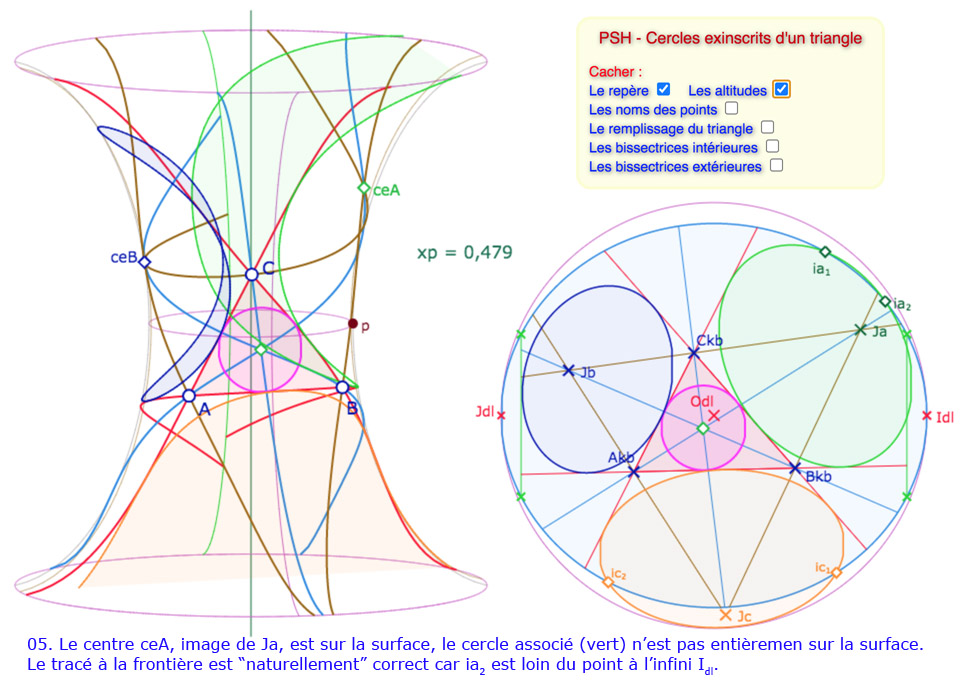
Galerie de 10 illustrations des cycles circonscrits
La figure associée
Les constructions des cercles exinscrits entièrement sur la surface ne posent aucun problème. Pour les cercles partiels ou les équidistantes, la programmation est faite pour une situation globale – décrite dans le disque de Beltrami – qui place le cercle exinscrit bleu en haut à gauche (autour du point \(J_{dl}\)), le cercle exinscrit vert en haut à droite, autour du point \(I_{dl}\), et le cercle exinscrit orange en dessous, plus ou moins au centre.
Les cycles exinscrits sur la PSH
Préférer ouvrir cette figure dans un nouvel onglet