Les droites idéales étant définies, reste à installer la polarité. Bachmann distingue deux grands cas :
• celui où l’axiome du rectangle est vérifié, qu’il appelle le « cas singulier » (revoir la séparation des géométries). Ce cas est plus simple à cause de la conservation des couples (pôle, polaire) par les demi-rotations.
• celui du cas dit « ordinaire » où l’axiome du rectangle n’est pas vérifié, plus complexe à traiter. Comme nous illustrons son propos avec la géométrie hyperbolique, c’est ce cas « ordinaire » que nous allons aborder dans cette page.
Construction plus générique des demi-rotations produisant une
droite idéale propre associée à une droite idéale
Avant cela, revenons sur les constructions des droites idéales propres associées aux droites idéales. En effet, dans la page précédente sur les droites idéales, nous avions toujours une demi-rotation \(H_{uv}\) donnée préalablement, ce qui déterminait entièrement la droite idéale propre \(H_{uv}(a)\) pour une droite \(a\) donnée, alors que la définition dit qu’il doit exister une demi-rotation \(H_{uv}\) telle que …
Dans cette section, nous allons utiliser la richesse de la géométrie dynamique pour réaliser des figures plus ouvertes à la variation, en particulier où la demi-rotation est à finaliser. On se propose ainsi de construire l’unique demi-rotation \(H_{uv}\) qui convient à une configuration où un point idéal hyperbolique de la droite idéale propre image est donné préalablement.

Sous forme de mini narration de recherche, commençons par le cas le plus simple, celui où la droite \(a=(a_1a_2)\) coupe le cercle horizon en \(iM_1\) et \(iM_2\).
Le point \(O\) est donné, a priori considéré comme fixe dans la théorie. On se donne deux point idéaux – sur le cercle horizon, \(u\) et \(M\) : \(u\) pour que \((Ou)\) soit une première droite de la demi-rotation, et \(M\) pour que la droite hyperbolique, à chercher, \(d=(MN)\) soit la partie hyperbolique de la droite \(g(d)\) telle que \(g(d)=H_{uv}(a)\), où bien entendu il faut aussi construire la droite \(v\) solution.
Dans ce contexte la construction est très simple.
• construction du point \(N\) : on sait que \(d=(MN)\) contient le pied de la perpendiculaire à la partie hyperbolique de \(a\), à savoir la droite hyperbolique \((iM_1iM_2)\) issue de \(O\). C’est le point \(I\) ci-contre. La droite \(d\) est donc la droite hyperbolique \((IM)\), ce qui donne le point idéal \(N\) cherché.
• construction de la droite \((Ov)\), notée \((Ov_i)\) ci-contre (\(i\) pour « intérieur » au sens où la droite \((a_1a_2)\) coupe l’horizon). Le cercle hyperbolique de centre \(O\) passant par \(I\) coupe la droite hyperbolique \((MN)\) en le point \(I^{uv}\), par une propriété déjà largement utilisée dans les pages précédentes de la construction de l’image d’une droite par une demi-rotation. Ayant \(I^u\) (par inversion) et \(I^{uv}\), la droite cherchée \((Ov_i)\) est la médiatrice de ces deux points.
Dans la figure finale suivante, on pourra déplacer \(u\) pour voir que l’angle \(uOv_i\) est constant. On a construit l’image \(Huvk= H_{uv_i}(K)\) d’un point \(K\) de la droite \((a_1a_2)\).
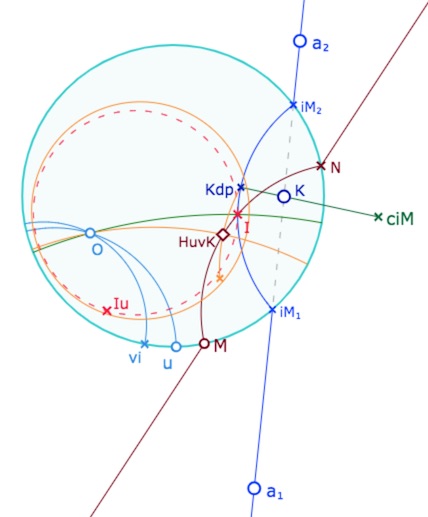
Toujours dans ce contexte où la droite idéale \(a\) coupe le cercle horizon, on reprend la construction spécifique – obtenue par une macro réalisée dans les figures de la page précédente – quand \(H_{uv}(K)\) est à l’intérieur du cercle \(C_{uv}\) défini à cette page et utilisé à la page précédente.
On rappelle que \(K\) étant un point de la droite affine \((a_1a_2)\), quand il est entre \(iM_1\) et \(iM_2\), on le projette sur la partie propre de la droite, en \(K_{dp}\) dont l’image est le milieu de \(K_{dp}\) et \(K_{dp}^{uv}\), point encore noté \(H_{uv}(K)\) obtenu comme intersection du segment et de la médiatrice des deux points. (les deux en orange ci-contre).
On a aussi ajouté dans cette illustration le cercle \(C_{uv}\) dont l’intérieur est l’image du plan hyperbolique par la demi-rotation \(H_{uv}\).
Abordons maintenant le cas où la droite \(\mathbf{a=(a_1a_2)}\) ne coupe pas le cercle horizon.
En fait nous allons proposer une construction générale du point \(N\), élémentaire, qui fonctionne aussi pour le cas précédent, d’où la démarche de « mini narration de recherche » pour la partie précédente, puisque nous avons nous-même commencé par ce cas simple, avant d’arriver à la construction suivante.
Cette page, étant consacrée à la polarité, nous allons simplement décrire la construction retenue. La preuve générale de cette construction sera l’objet d’un des nombreux prochains articles de blog relatifs à ce menu sur l’axiomatique de Bachmann. On s’intéresse à la construction du point \(N\) de l’illustration de gauche. L’illustration de droite montre qu’elle fonctionne aussi dans le cas où la droite \(a=(a_1a_2)\) coupe le cercle horizon.
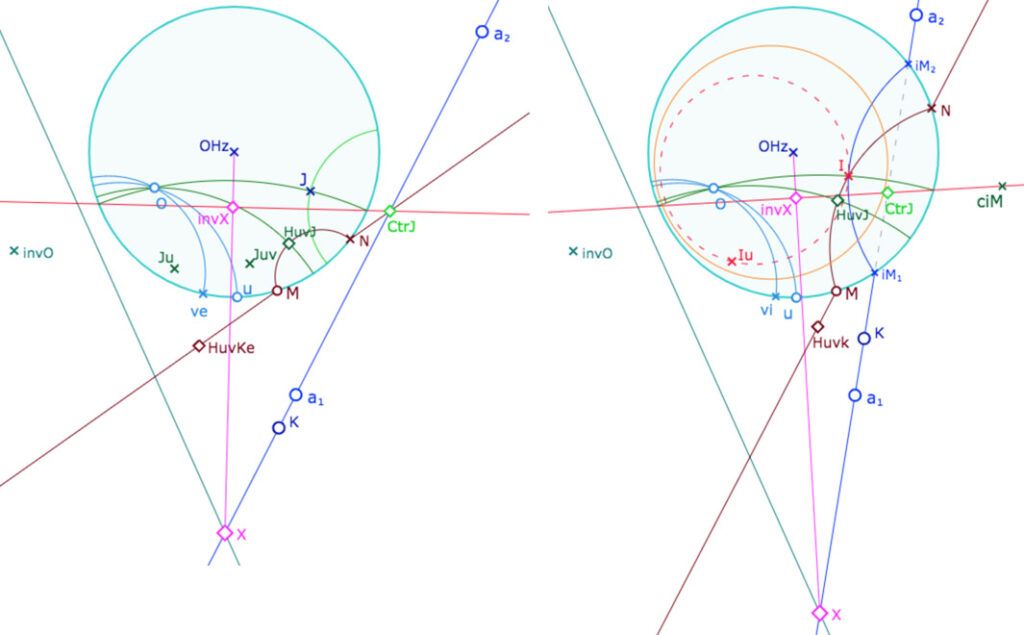
La médiatrice de \(O\) et de son inverse \(invO\) par rapport au cercle horizon coupe la droite \(a\) en \(X\). On note \(invX\) son inverse par rapport à l’horizon. La perpendiculaire à \((X \, O_{hz})\) en \(invX\) coupe la droite \(a\) en \(CtrJ\). Le point \(N\) est la seconde intersection de \((M \, CtrJ)\) avec l’horizon. On appelle \(J\) le pied de la perpendiculaire issue de \(O\), à la droite hyperbolique de centre euclidien \(CtrJ\). Alors – c’est ce qu’il faut montrer – le pied de la perpendiculaire à la droite \((MN)\) issue de \(O\) est l’image de \(J\) par la demi-rotation qui envoie la droite idéale \(a\) en la droite idéale propre \(g(MN)\), autrement dit \(H_{uv}(J)\). Ce qui détermine \(J^{uv}\) et donc la seconde droite \((Ov_e)\) médiatrice de \(J^{uv}\) et \(J^u\). Enfin on note \(Huvke= H_{uv_e}(K)\) l’image de \(K\) par \(H_{uv_e}\).
Dans l’illustration de droite, on voit l’on pourrait redéfinir le point \(I\) comme l’intersection des droites hyperboliques \((MN)\) et \((iM_1iM_2)\).
La figure dynamique associée
En plus des manipulations proposées dans les commentaires, observer que quand on déplace \(M\), par construction, \(J\) est invariant
Préférer ouvrir cette figure dans un nouvel onglet.
Cette figure sera utilisée en fin de page …
Polarité primitive
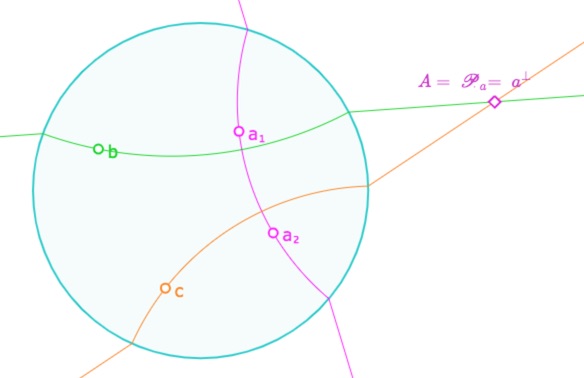
Bien entendu, l’orthogonalité des droites du plan métrique induit une orthogonalité des droites idéales propres. Il en résulte que, pour une droite \(a\) du plan métrique, la droite idéale propre \(g(a)\) est la polaire de \(\mathscr{P}_a\), le point idéal associé aux dstruction J est invariantroites du faisceau d’axe \(a\), ce qui peut s’illustrer comme ci-contre.
Bachmann appelle cette situation la polarité primitive : pour toute droite du plan métrique \(a\), la droite \(g(a)\) et le point idéal \(\mathscr{P}_a\) sont pôle et polaire l’un de l’autre.
Pour aller au delà, Bachmann propose de faire, pour l’orthogonalité, ce qui a été fait pour l’incidence : les droites idéales ont été définies à partir des droites idéales propres, elles-mêmes en bijection avec les droites du plan métrique. De même, la polarité entre points idéaux et droites idéales va être définie, par les demi-rotations, à partir des polarités primitives, directement associées aux droites du plan métrique.
Pour la définition des droites idéales, il avait commencé par vérifier l’action des demi-rotations sur les droites idéales propres : nous avions illustré la relation \(H_{uv}(g(a))=g(H_{uv}(a))\).
Ici, il n’y a aucune possibilité qu’un couple de polarité \((a, A)\) soit conservé par les demi rotations puisque celles-ci ne conservent pas l’orthogonalité (contrairement au « cas singulier »). La situation est donc un peu plus complexe.
Image réciproque d’un point (idéal impropre) par une demi-rotation

Pour illustrer la définition générale de la polarité, il faut d’abord savoir construire l’image réciproque d’un point (en pratique idéal impropre suffira) par une demi-rotation \(H_{uv}\).
Compte tenu des propriétés de l’axe du pinceau image d’un pinceau à axe (rappelées et utilisées en début de la page précédente), on est conduit, étant donnés une droite \(a\) et le point \(A=\mathscr{P}_a\), à construire une droite \(d\) telle que \(a\) soit la bissectrice (ne passant pas par \(O\) de \(d\) et \(d^{uv}\). Le centre euclidien de \(d, \; A’=\mathscr{P}_d\) sera l’antécédent cherché.
Pour cela, on peut considérer \(I\) le pied de la perpendiculaire à \(a\) issue de \(O\). La droite \((II^{uv})\) est la droite image par la rotation \(uv\) de la droite \(d\) cherchée. Il suffit de construire l’antécédent \(K^{vu}\) d’un point \(K\) de cette droite pour conclure. On pourrait vérifier la construction en appliquant la macro d’image d’un pinceau à axe par \(H_{uv}\) … mais ce n’est même pas la peine, la construction est assez évidente.
Rappel des notations : si \(H_{uv}(a)\) désigne simplement l’image de la droite métrique a par \(H_{uv}\), on note \(H_{uv}(\mathscr{P}_a\)) soit le centre soit l’axe de l’image du faisceau d’axe \(a\) par \(H_{uv}\).
Le théorème suivant est celui qui traite de l’image par une demi- rotation \(H_{uv}\) d’un couple de polarité primitive \((g(a),\mathscr{P}_a)\)pour une droite métrique \(a\).
Si, pour une droite du plan métrique \(a, \; A=\mathscr{P}_a\) est le pôle de \(g(a)\), alors pour une demi-rotation \(H_{uv}\) le pôle de la droite idéale propre \(g(H_{uv}(a))\) est le point \(H_{vu}^{-1}(A)\).
Dans la figure suivante, on a ajouté deux droites \(m\) et \(n\) orthogonales à \(H_{uv}(a)\), alors on vérifie que \(g(m)\) et \(g(n)\) sont sécantes en \(H_{vu}^{-1}(A)\).
On peut agir sur les poignées \(a_1\) et \(a_2\) de la droite \(a\), ou sur les poignées \(m\) et \(n\) des droites du même nom.
Agir aussi sur \(u\) ou \(v\), en plaçant l’un sur l’autre – même si c’est exclu de la définition des demi-rotations – pour voir le point \(H_{vu}^{-1}(A)\) traverser \(A\).
Ce résultat étant acquis, on peut maintenant définir la polarité pour des points ou droites idéales quelconques en étendant le résultat sur la polarité primitive.
Droite idéale et point idéal en polarité
Définition : une droite idéale \(a\) et un point idéal \(A\) sont dit en polarité s’il existe une demi-rotation \(H_{uv}\) telle que \(a=H_{uv}(g(b))\) et telle que \(H_{vu}^{-1}(A)=\mathscr{P}_b\), c’est-à-dire concrètement \(A=H_{vu}(\mathscr{P}_b)\).
Dans cette définition, l’important est l’existence d’une rotation \(uv\) et non la rotation elle-même. En effet, cette définition n’a un sens que si elle est indépendante de \(u\) et \(v\) (incidentes à \(O\)), ce que montre Bachmann. C’est aussi pour illustrer cela le plus généralement possible que la figure de la section d’introduction a été mise en œuvre.
Illustration hyperbolique
Nous allons voir ce que cela donne dans le cas du modèle du disque de Poincaré. Les lecteurs qui découvrent cette problématiques de plongement projectif peuvent être agréablement surpris de la simplicité et de la cohérence du résultat alors que les lecteurs plus familiers des questionnements projectifs peuvent au contraire être presque déçu (« quoi tout ça pour ça ! ») d’un résultat finalement assez trivial : tout simplement, il n’y a pas d’autres options, donc on retrouve ce que l’on peut connaître par ailleurs : dans ce modèle, la polarité est tout simplement celle par rapport au cercle horizon (comme présentée dans la page de présentation modèle de Klein Beltrami).
Cette illustration sur le cas hyperbolique réel ne doit toutefois pas faire oublier l’aspect très général, profond, des méthodes utilisées et des théorèmes montrés par Bachmann, indépendamment d’un type de géométrie spécifique. C’est juste l’illustration qui est triviale, pas la démarche de Bachmann.
Pour utiliser la macro mentionnée dans l’illustration ci-dessous, et qu’elle ne produise qu’un seul point pour les deux cas, on a modifié la figure initiale en introduisant le point \(v_{ie}\) qui est, selon leur existence, soit \(v_i\) soit \(v_e\) de la figure de départ. Par ailleurs on rappelle que le point \(N\) est unique : c’est le même que la droite \(a\) coupe, ou non, le cercle horizon. Il en est donc de même de la droite \((MN)\).
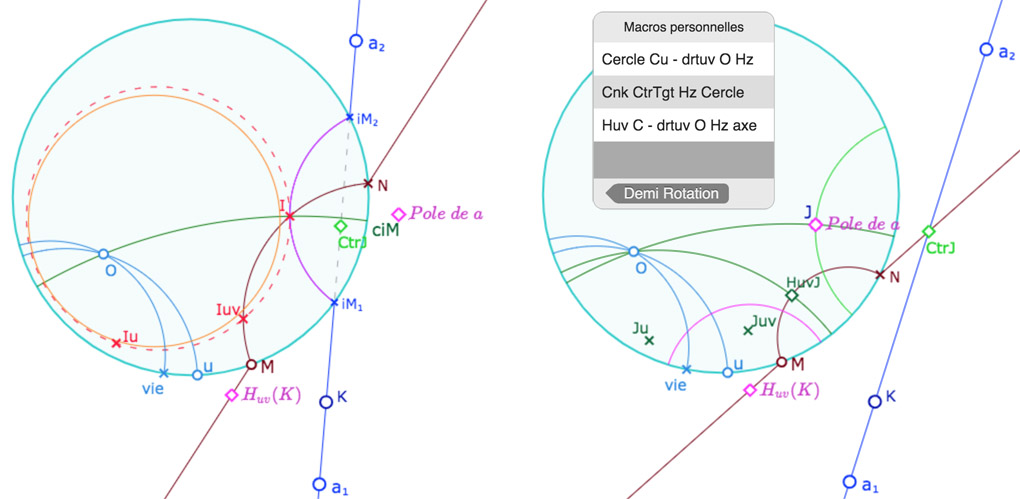
Dans cette figure, on applique la troisième macro aux droites \(v, u\), puis le point \(O\),
le cercle horizon, et la droite hyperbolique \((MN)\).
Quand la droite \(a\) coupe l’horizon, le pôle de \(a\) est, assez trivialement vu la polarité primitive, le centre \(c_{iM}\) de la partie hyperbolique de la droite.
Quand la droite \(a\) ne coupe pas l’horizon, le pôle de \(a\) est le point \(J\) de la section d’introduction qui a servi à construire la demi-rotation solution.
Manipuler la figure dynamique
Préférer ouvrir cette figure dans un nouvel onglet.
Indépendance de la polarité vis à vis du point \(O\)
La cohérence de cette définition va plus loin. En effet, Bachmann montre ensuite – plus tard dans son exposé – que la définition du couple de polarité est aussi indépendante du point \(O\) choisi initialement.

Si dans la théorie générale, il y a bien entendu quelque chose à montrer, pour ce qui est de nos illustrations, sachant que depuis un point \(O\) quelconque; on arrive à construire le pôle de \(a\) par rapport au cercle horizon, il n’y a rien de particulier à illustrer.
Mais on peut s’amuser quand même à l’illustrer rapidement, en vérifiant, dans le cas où la droite \(a\) ne coupe pas l’horizon, que la construction du point \(J\) des figures précédentes est indépendant de \(O\).
Ouvrir cette figure dans un nouvel onglet pour agir sur les deux points \(O_1\) et \(O_2\).
Rappel de la construction :
• la médiatrice entre un point \(O\) et son inverse par rapport à l’horizon coupe la droite \(a\) en le point \(X\).
• La perpendiculaire à \((O_{hz}X)\) en l’inverse de \(X\), noté \(invX\) coupe la droite \(a\) en \(CtrJ\).
On construit ainsi les deux points \(CtrJ_1\) et \(CtrJ_2\). Puis les droites hyperboliques de centre euclidien ces deux points. Ensuite le point \(J\), est l’intersection de la droite hyperbolique et de sa perpendiculaire issue de \(O\).
On construit ainsi \(J_1\) et \(J_2\) qui coïncident avec l’inersection des deux troites hyperboliques de centres \(CtrJ_1\) et \(CtrJ_2\).
Là encore un article du site reviendra sur ce résultat qui n’est – pour ce modèle bien entendu – qu’une conséquence des propriétés de l’inversion.
Les conclusions de Bachmann
Mais avant cela, Bachmann montre que la relation pôle-polaire ainsi définie sur les droites idéales générales est bien une polarité projective – c’est-à-dire une corrélation involutive (en utilisant le théorème d’antiappariement) et donc que le plan idéal ainsi construit est bien un plan projectif métrique dans lequel l’orthogonalité dans le plan métrique initial coïncide avec celle qui découle de la polarité nouvellement construite.
La symétrie orthogonale par rapport à une droite \(a\) du plan métrique se prolonge en une homologie harmonique (de centre \(\mathscr{P}_a\) et d’axe \(g(a)\)) dans le plan idéal. Il en résulte le théorème auquel Bachmann voulait arriver : celui de Dehn, obtenu par une démarche essentiellement algébrique, et dans un contexte beaucoup plus général :
Tout plan métrique peut être représenté comme un sous-ensemble d’un plan projectif métrique. Le groupe des transformations du plan métrique est alors isomorphe à un sous- groupe du groupe des transformations du plan métrique projectif.
On poursuivra, ultérieurement, dans d’autres pages, ou des articles de blog, sur la question de l’algébrisation qui en découle, avec en particulier un exemple, de Daniel Perrin, de géométrie où il existe un autre type de pinceaux sans support que le cas « simple » de la géométrie hyperbolique. En attendant, voici une application immédiate, celles des hauteurs – et de l’orthocentre puisque l’on est dans un plan projectif – dans le plongement du disque de Poincaré
Hauteurs et orthocentre dans le plongement de DP
Une fois que l’on a réalisé une macro générique de « droite idéale pour DP », on est tenté de construire les hauteurs d’un triangle car pour tracer une hauteur, il suffit de construire la perpendiculaire à la droite d’un côté passant par le sommet opposé. Et la perpendiculaire passe par le pôle de la droite, donc c’est tout simple

Dans cette illustration on a détaillé les angles droits des hauteurs.
On a noté \(c_Xp_{YZ}\) le centre de l’arc de la droite idéale propre passant par \(X\) et le pôle de \((YZ)\).
Dans l’illustration précédente, tout fonctionne bien car les trois pôles des droites sont extérieurs à l’horizon : ce sont les centres des arcs de cercle de la partie hyperbolique des droites idéales propres.
Mais dans l’illustration suivante, le pôle de \((BC)\) est intérieur à l’horizon, et la droite idéale propre passant par \(A\) et ce point \(poleBC\) n’est pas orthogonale à \((BC)\). On voit que les (fausses) « hauteurs » ne sont pas concourantes. On l’illustre plus précisément en ajoutant la KH-mesure de l’angle des demi-droites en \(K\) comme cela a été présenté dans cet article sur les distances et les angles de l’approche de Daniel Perrin dont les macros produites sont applicables ici.
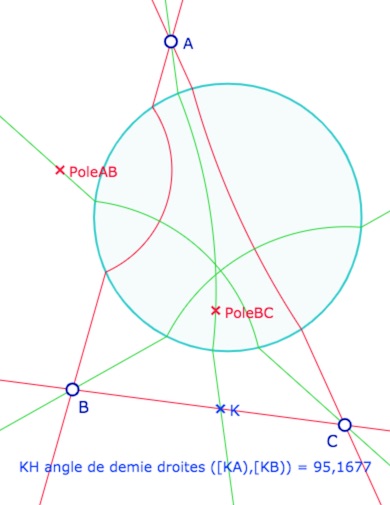
En fait, dans le cas ci-dessus, c’est la droite affine passant par \(A\) et \(PoleBC\) qui est orthogonale à la droite \((BC)\), à partir de laquelle on construit la droite idéale propre associée … qui, elle, ne passe pas par le pôle de la droite quand celui-ci est intérieur au cercle unité.
Voici quelques illustrations de la figure suivante
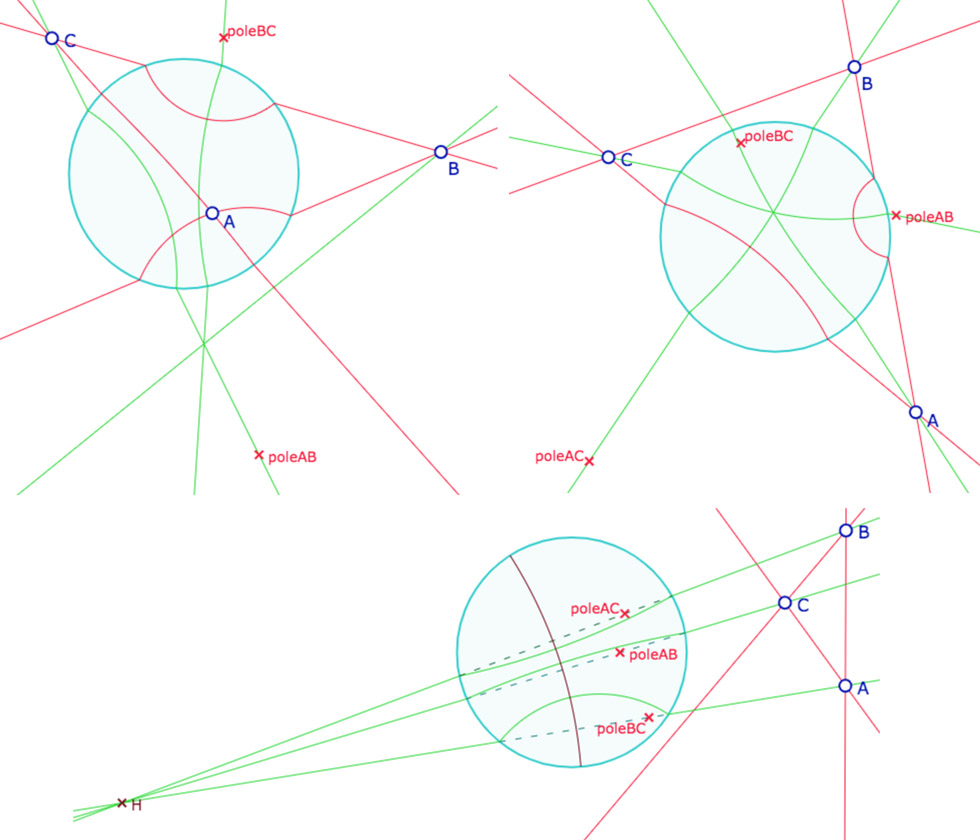
En haut à gauche, une des hauteurs est une droite idéale, l’orthocentre est un point idéale impropre.
En haut à droite, l’orthocentre est un point idéal propre. On voit que la hauteur issue de \(A\) ne passe pas par le pôle de \((BC)\).
En bas, on détaille la construction des droites idéales propres, avec les droites affines passant par les pôles. L’orthocentre – impropre – est alors le centre euclidien de la perpendiculaire commune aux parties hyperboliques des trois hauteurs comme droite idéales propres.
Manipuler la figure dynamique associée
On peut agir sur les sommets \(A, B\) et \(C\). On déplace la figure à la souris.
Attention : si vous agrandissez le cercle unité, en tirant dessus, il faut modifier les sommets sinon la figure n’est pas mise à jour.
Préférer ouvrir cette figure dans un nouvel onglet (plus grande). Même remarque sur la modification du rayon du cercle horizon.