Cette page ne contient que 4 figures, mais deux sont assez lourdes. Ne pas hésiter, si elles ne se chargent pas complètement à les relancer avec la première icone à gauche de l’iframe concernée, parfois il faut cliquer deux fois : cela dépend de l’état des serveurs engagés (celui qui héberge le site et celui qui héberge DGPad).
A propos des figures ouvertes hors iframe dans un nouvel onglet (pour tout les items du menu): selon le navigateur, pour qu’on puisse tourner la surface au simple clic, il peut être nécessaire de désélectionner la flèche de gauche du tableau de bord, même si elle paraît désélectionnée.
Dans cette page, on reprend la construction d’abord du cercle de pavage de P(5,4) et de P(4,5), en particulier à partir des calculs présentés en détail dans ce post de blog sur autour du pentagone orthogonal la pseudosphère, en ayant transformé la KB-construction en macro-construction. Mais comme la surface PSH couvre beaucoup plus du plan hyperbolique que la PS, on va essayer de construire 4 pentagones orthogonaux autour d’un point.
Pentagone orthogonal
Compte tenu de ce qui a été fait précédemment, la construction est rapide : il suffit d’agencer quelques macro-constructions, parfois de les optimiser par une approche algébrique plutôt qu une construction géométrique.
Dans ces figures, on se donne un centre du pentagone sur la surface, le point \(O\) ci-dessous. Même si, bien entendu ,le pentagone a toujours la même taille (puisqu’il n’existe qu’un seul pentagone orthogonal hyperbolique), selon la position du centre on a l’impression que le pentagone se déploie plus ou moins sur la surface. C’est intéressant à observer sur la figure suivante. On revient dessus un peu plus loin.
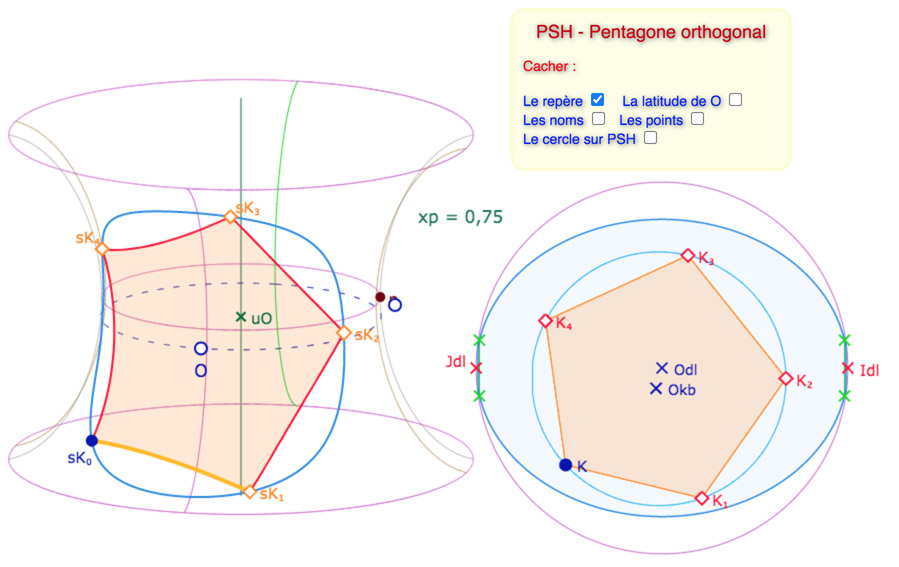
Pour p=0,75 le pentagone orthogonal prend beaucoup de place de la feuille principale. Plus de la moitié en terme de longitude.
Mais pour p=0,25 le même pentagone se déploie sur trois feuilles, plus précisément dépasse la feuille principale des deux côtés.
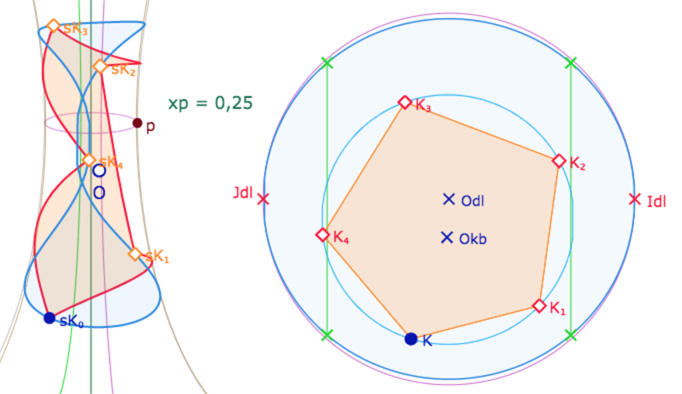
Figure à manipuler
On peut agir sur \(K\) mais aussi sur le centre du cercle \(O\) et sa latitude \(u_O\).
On peut préférer ouvrir la figure dans un nouvel onglet
Pavage P(5,4) : 4 pentagones orthogonaux autour d’un point
On vient de voir que plus le centre du pentagone s’éloigne des frontières de la feuille principale, plus le pentagone se déploie sur la feuille. Il en résulte que si on veut que 4 pentagones orthogonaux, répartis autour d’un point, puissent entrer tous sur la surface, il faut placer le centre assez proche d’une des frontières de la feuille principale et même si possible, au delà, sur la feuille précédente par exemple. En effet, on a vu dans la page d’introduction à la PSH, que la seule façon d’aller vers l’infini sur cette surface est de s’enrouler sur elle-même. Ainsi, si on arrive à placer le centre du cercle initial de pavage, sur la deuxième ou troisième feuille, comme les pentagones sont toujours de même taille, ils apparaissent plus petits dans la représentation (comme pour les pavages de DP quand on s’approche de l’horizon), et on peut mettre plus de pentagones. On pourrait même réaliser un véritable pavage de génération 1.
En pratique, dans ces constructions, on place des points de base seulement sur la feuille principale. Aussi, pour que 4 pentagones orthogonaux, répartis autour d’un point, puissent entrer tous sur la surface, il faut, de fait, placer le centre sur l’axe vert de longitude \(-\pi\) ou juste de l’autre côté pour une longitude de \(+\pi\). En effet, si on peut toujours arriver à placer, artificiellement, avec une case à cocher comme sur les exemples de la PS, un point de base sur la feuille précédent la feuille principale, la macro de construction du cercle de pavage du pentagone orthogonal dans KB, peut-être faite un peu vite, ne fonctionne plus (un point à reprendre pour de prochaines constructions). On invite donc les utilisateurs de la figure suivante de toucher à la latitude \(u_O\) mais pas vraiment à \(O\) (sauf pour jouer …).
Quand 4 pentagones rentrent sur la surface c’est souvent sur plus d’une feuille (pas toujours, ce n’est pas « tout à fait » le cas à l’ouverture de la figure). Il est parfois difficile de voir correctement la répartition des pentagones. C’est pour cela qu’on a favorisé de nombreuses options d’affichages comme celles-ci :

Deux pentagones dans le sens vertical de la surface.
On a choisi une « grande » valeur de \(p\) : les deux pentagones colorés rentrent juste dans la surface.
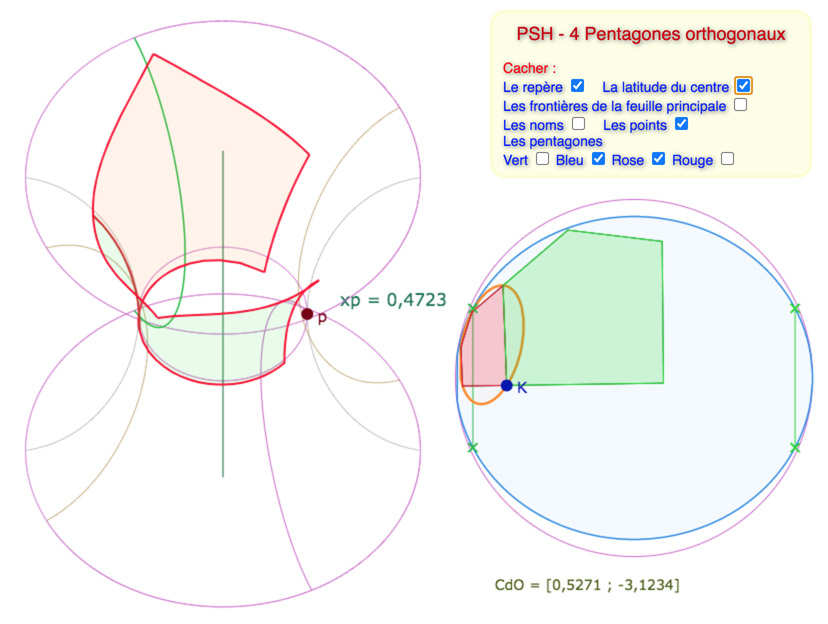
Deux pentagones dans le sens horizontal de la surface : on voit bien ici qu’on ne dépasse pas une amplitude de \(2\pi\).
On voit sur KB que dans ce contexte précis (position de \(K\)), au moins deux points sortent de la surface.
Et la figure complète ressemble plus à cela …
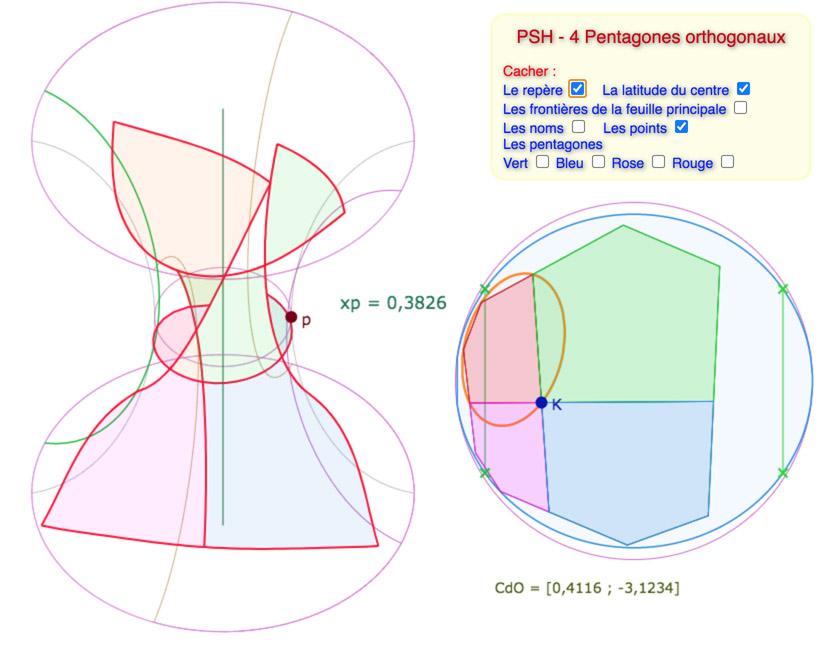
Sur KB,on voit clairement que certains sommets sont sur la feuille avant la feuille principale.
Pour autant, l’ensemble est réparti sur une amplitude de longitude inférieure à \(2\pi\) et donc ne se chevauche pas.
Figure à manipuler
Conseils d’utilisation :
• Pour s’approprier la figure, commencer par explorer les pentagones 2 par 2 avant de les afficher tous les 4.
• Les pentagones sont tracés même s’ils sortent de la surface. En effet, les calculs de retour sur la PSH sont calculés pour tous les points de KB. On aurait pu sophistiquer un peu plus la figure, mais cela l’aurait fortement complexifiée, elle serait alors moins réactive.
• Quand on tourne un peu trop la surface, on peut parfois être perdu quant à l’orientation effective de la figure. Faire réapparaître le repère pour bien se placer dans un contexte de repère direct. Parfois il suffit d’un petit déplacement vertical car c’est juste question de perception du repère.
Pour ce qui est des points, on déplacera essentiellement la latitude de \(O\), le point \(u_O\)
et le point \(K\) sur le cercle de pavage dans KB, pour faire tourner les 4 pentagones sur la PSH.
On peut préférer ouvrir cette figure dans un nouvel onglet
Pavage P(5,4) : 5 carrés de 72° autour d’un point
Le cercle de pavage est le même, il suffit de partir de la figure précédente et de la modifier simplement pour construire un premier carré d’angles aux sommets de 72°.
On poursuit par le pavage lui-même. Comme ci-dessus, avant de proposer la figure à manipuler, on commence par présenter les options d’affichage pour mieux voir les différents carrés.
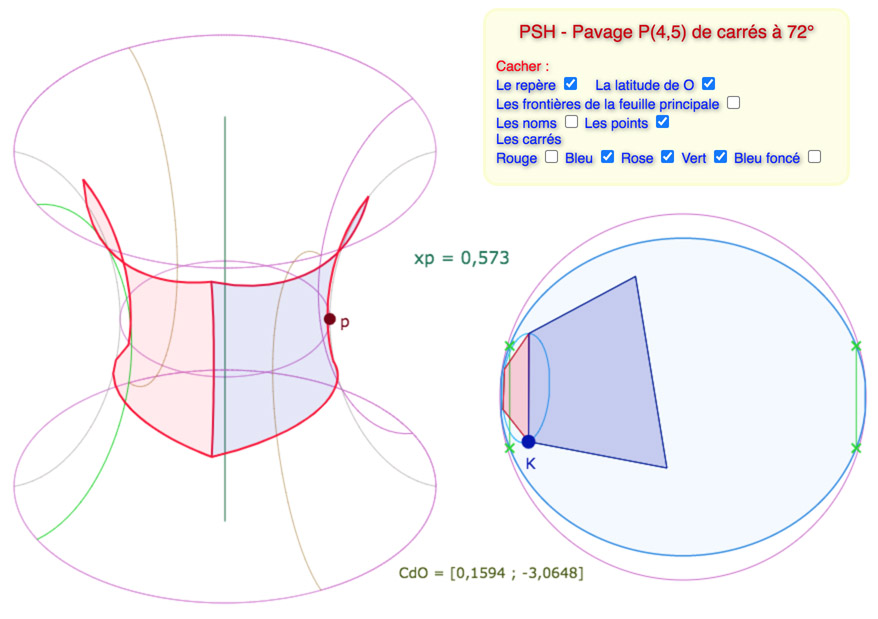
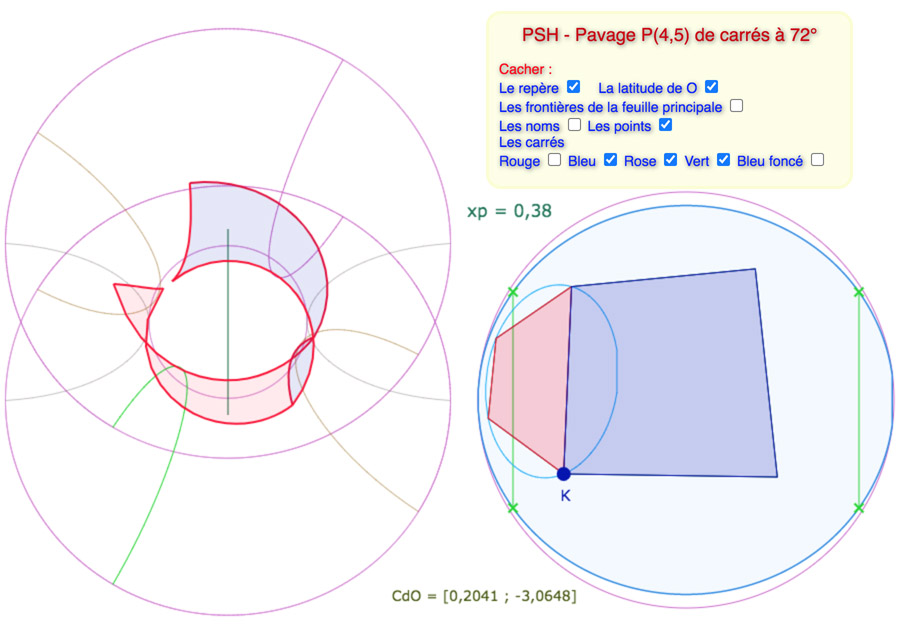
Tout d’abord deux carrés « horizontaux », avec deux valeurs de \(p\), bien différentes.
La première couvre une envergure de longitude inférieure à \(\pi\), la seconde se rapproche d’un tour complet.
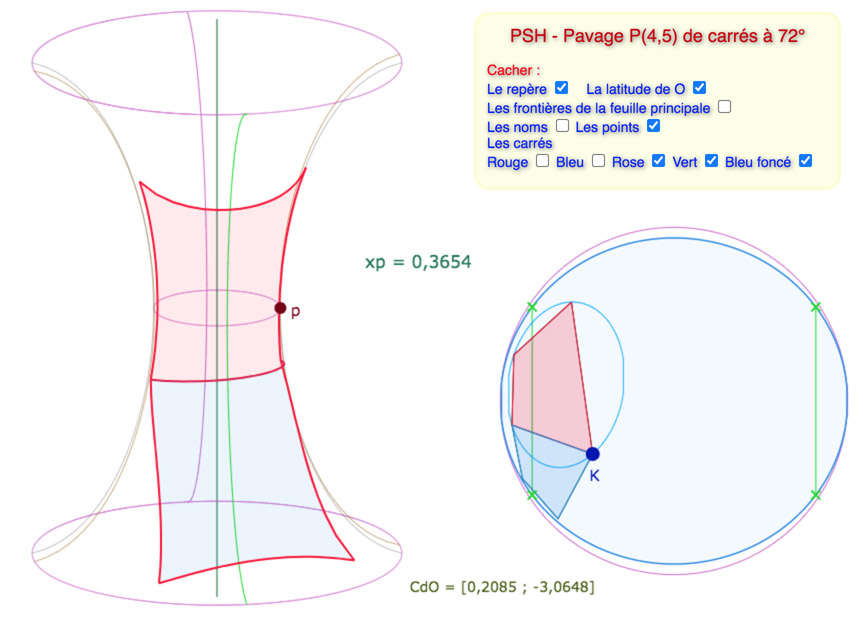
Et un exemple de deux carrés en position « verticale »
Puis on peut afficher 3 ou même 4 carrés …
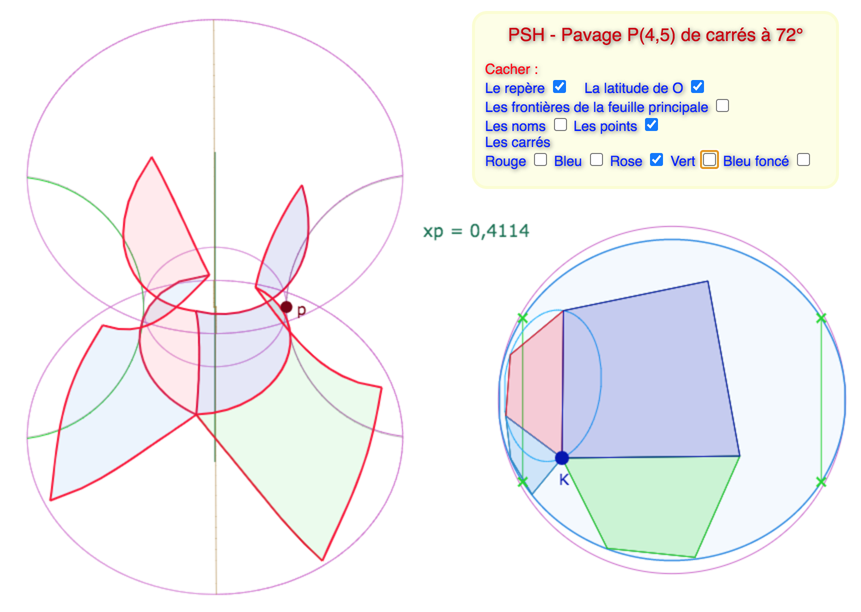
Les 5 carrés vus de dessus : on voit qu’ils se superposent partiellement car ils ne sont pas sur la même feuille.
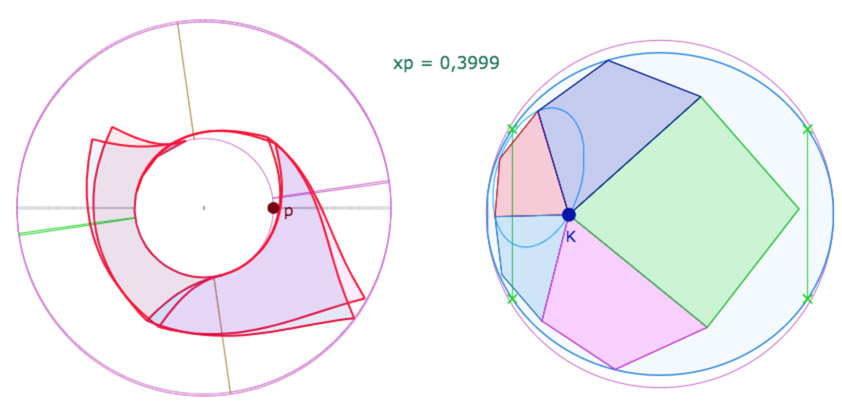
Manipuler la figure
Les conseils d’utilisation de la figure précédente s’appliquent aussi à cette figure
Faire apparaître les points pour voir les correspondances entre KB et la PSH . Penser à déplacer \(K\) et modifier \(p\).
A l’ouverture, les 5 carrés couvrent plus d’un tour de longitude. Faire tourner la PSH pour y voir plus clair.
Reprendre aussi des variantes des illustrations précédentes pour s’approprier plus simplement la configuration.
Préférer ouvrir cette figure dans un nouvel onglet