Dans son ouvrage sur les fondements de la géométrie, Jacqueline Lelong-Ferrand (JLF) avait cette remarque : finalement, on modifie un axiome de base sur cinq, et globalement, d’une certaine façon, la géométrie hyperbolique reste à 80% euclidienne.
Une géométrie loin de nos représentations
Avec la géométrie elliptique, on supprime un autre axiome, et, dans la présentation de JLF, un axiome essentiel puisqu’il porte sur les isométries fondamentales, celui qui assure l’existence d’un pliage. Il va en résulter une géométrie non orientée, bornée, très éloignée de nos propres représentations géométriques. Par exemple un triangle (trois points) peut avoir 4 cercles circonscrits distincts. Il aura fallu la profondeur de géomètres comme Riemann, les capacités synthétiques de Klein, après les travaux de Cayley pour que la géométrie elliptique ait droit de cité en tant que telle.
Une axiomatique générale tardive
Axiomatiquement aussi il a été délicat d’intégrer la géométrie elliptique. Les axiomatiques absolues usuelles incorporent, puis séparent les géométries euclidiennes et hyperboliques : soit par un point il passe une seule parallèle à une droite donnée, soit il en passe plus d’une. Mais ces approches «absolues», en général, compte tenu de leurs axiomes, ne peuvent pas intégrer la géométrie elliptique, parce que, par exemple pour les plus générales, justement la symétrie orthogonale est un pliage, ce qui exclu le cas elliptique. Même si ce type de géométrie était très pratiqué, depuis longtemps, puisqu’il s’agit, d’une certaine façon, d’une géométrie projective, avec sa notion de polarité, Il faudra attendre le tiers du XX°s pour que des premières tentatives d’axiomatisation génériques émergent et le milieu du XX°s pour que l’axiomatique la plus aboutie en ce domaine, celle de Bachmann, puisse traiter aussi bien des trilatères hyperboliques que des pôles et polaires elliptiques. Car une particularité de cette géométrie est que, du point de vue des éléments caractéristiques des isométries, d’un certain point de vue, il n’y a pas de différence entre un point et une droite, ce qui nécessite de repenser l’incidence dans son rapport à l’appartenance.
Une bonne représentation : le quotient de la sphère
par l’équivalence des points diamétralement opposés
Pour des raisons liées aussi bien à la navigation qu’à l’astronomie, la géométrie de la sphère est connue depuis très longtemps. C’était même un domaine à part entière, la sphérique, dont on connait, dès le XVII°s, toutes les formules, qu’elles portent sur les angles (trigonométrie sphérique), ou sur l’aire d’un triangle sphérique, et sa proportionnalité à l’excès angulaire \(\widehat{A}+\widehat{B}+\widehat{C}-\pi\).
Pour autant la sphérique n’est pas considérée comme une géométrie, pas parce que les droites y sont bornées mais parce que cette éventuelle « géométrie » ne vérifierait pas le premier axiome d’incidence qui veut que par deux points il passe une et une seule droite. Or sur la sphère, les droites sont les grands cercles. Avant Gauss, le résultat était connu en terme de «plus courte distance». Depuis Gauss, on le sait plus formellement avec la géométrie intrinsèque des surfaces. Désormais, les géodésiques sont définies, et celles de la sphère sont les grands cercles. Or par deux points diamétralement opposés il passe une infinité de grands cercles, et donc la sphère ne peut pas correspondre à une géométrie plane vérifiant le premier axiome d’incidence. D’où l’idée d’identifier les points diamétralement opposés. Ensuite Klein projette le demi hémisphère du pole sud dans le plan tangent au pole sud par une projection stéréographique – pour avoir un modèle conforme – de pôle le pôle nord.
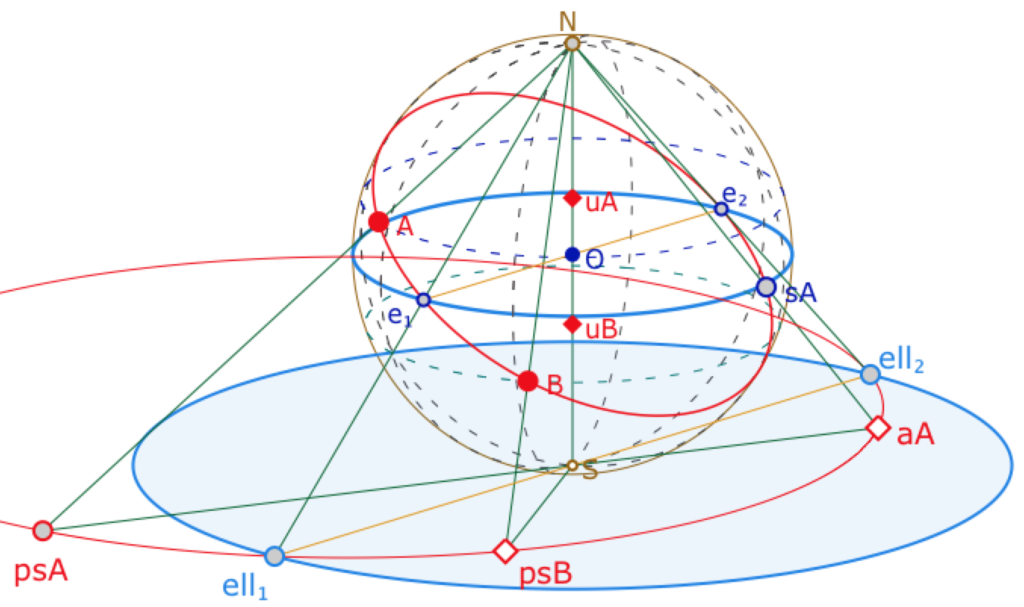
Dans la figure suivante les points \(A\) et \(B\) se manipulent par \(u_A\) et \(u_B\) qui fixent leurs côtes, puis sur leurs parallèles à l’équateur. Le grand cercle \((AB)\) coupe l’équateur en \(e_1\) et \(e_2\) qui se projettent stéréographiquement en \(ell_1\) et \(ell_2\).
\(A\) étant au dessus de l’équateur, par identification des points diamétralement opposés, on projette son symétrique \(s_A\) en \(a_A\), composée que l’on appelle l’antipodie elliptique. Les points \(ps_A\) et \(ps_B\) sont les projeté stéréographiques de \(A\) et \(B\). L’image du grand cercle \((AB)\) est un cercle qui passe par ces trois points et coupe l’horizon aux points diamétralement opposés \(ell_1\) et \(ell_2\). Sa trace à l’intérieur de l’horizon est la droite elliptique du modèle de Klein.
Antipode elliptique spatiale et plane
Elles sont toutes les deux la composée commutative de la symétrie centrale (de centre \(O\) pour l’espace, de centre \(S\) pour le plan) et de la projection stéréographique (espace) ou de l’inversion (plan). Ainsi, \(ps_A\) est l’inverse du symétrique de \(a_A\) par rapport à \(S\) et \(a_A\) est l’inverse du symétrique de \(ps_A\) par rapport à \(S\).
Déplacer \(B\) sur son parallèle pour voir que toutes les droites elliptiques issues de \(A\) passent par \(s_A\) et \(ps_A\).
La figure est faite pour \(A\) qui reste au dessus de l’équateur (on fait son antipode) et \(B\) en dessous (projection directe)

Ci-contre on a ramené dans le plan la trace des droites passant par \(B\) : \(B_1\) est le symétrique de \(B\) par rapport au centre de l’horizon et \(B’\) son inverse. On conservera le nom d’antipodie elliptique pour la transformation de \(B\) en \(B’\). D’une manière générale une macro construction point elliptique retiendra, pour un point quelconque, celui des deux qui est elliptique, c’est-à-dire dans le cercle horizon.
Simplification de la représentation du modèle
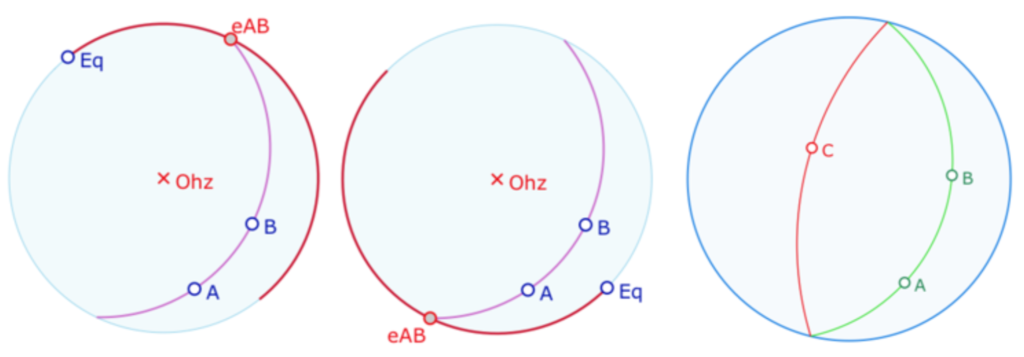
L’identification des points diamétralement opposés s’applique aussi à l’équateur, et donc les points elliptiques sont précisément les points à l’intérieur de l’horizon, les points sur l’horizon, identifiés à leur symétrique. Une autre façon de le dire est de considérer le modèle comme le disque horizon et la moitié (semi-ouverte) du cercle horizon. Ainsi, il faudrait, en tout rigueur, représenter le modèle comme les deux illustrations de gauche (ci-dessous), avec éventuellement un demi cercle fixé.
On choisira la simplification graphique, plus ergonomique, en omettant la partie du cercle appartenant au modèle sans oublier qu’il y a toujours un point sur le cercle. Ainsi sur la troisième illustration, la droite passant par \(C\) n’est pas parallèle à la droite \((AB)\), comme c’était le cas du modèle euclidien borné. Elles ont toutes les deux un point en commun, le point elliptique sur le cercle horizon, puisque les deux extrémités de chaque arc (du modèle) sont toutes les deux un représentant de cet unique point elliptique, de par « le quotient par équivalence des points diamétralement opposés ».