La symétrie orthogonale sur la sphère, comme dans le plan elliptique, ne pose pas de problème à définir ou à construire. Ses propriétés par contre peuvent surprendre quand on ne les a jamais rencontrées. Avec la géométrie sphérique, le symétrique d’un point par rapport à une géodésique de la sphère n’est rien d’autre que le symétrique euclidien de ce point par rapport au plan que défini la géodésique (un grand cercle).
Ci-contre une droite de la sphère (verte : grand cercle colorié pour mieux visualiser le plan en manipulation) construite comme polaire du point \(M\) (sur un cercle défini par sa latitude \(u_M\)). On se donne ensuite un point \(A\), sur un cercle de latitude \(u_A\). En rose la droite orthogonale à la précédente passant par \(A\), elle aussi remplie pour voir le plan euclidien associé, en manipulation directe.
\(H\) est le projeté orthogonal de \(A\) sur le plan euclidien associé à la droite de la sphère verte et \(symA\) le symétrique euclidien de \(A\) par rapport au plan et donc symétrique par rapport à la droite sur la sphère.
On projette par antipode elliptique. Par exemple \(A\) étant dans l’hémisphère nord, \(Aell\) est le projeté stéréographique de \(sA\) le point diamétralement opposé à \(A\).
De même \(symAell\), le symétrique elliptique de \(Aell\) par rapport à la droite elliptique verte, est le projeté du symétrique (croix rouge) de \(symA\), qui, dans cette illustration, est lui aussi dans l’hémisphère nord. Les droites étant orthogonales, celle passant par \(A\) et son symétrique \(Aell\) passe par le pôle \(P\) de l’axe de symétrie. Dans cette illustration, on peut conjecturer que l’intersection est bien le milieu des deux points.

Symétrie orthogonale ? Vraiment ?
Mais si l’intersection des deux droites est – par construction – le milieu du point \(Aell\) et de son symétrique \(symAell\), l’autre milieu des deux points sur la droite n’est autre que le pôle de l’axe de symétrie (car le premier milieu est sur l’axe). Èt ceci est vrai pour tous les points elliptiques puisque toutes les droites orthogonales à l’axe de symétrie passent par son pôle, on peut en déduire que :
La symétrie orthogonale elliptique par rapport à une droite est aussi la symétrie centrale par rapport à son pôle.
Dans la démarche théorique qui sous-tend cette présentation, les symétries orthogonales sont des éléments premiers, sur lesquels sont émis des axiomes. Certains auteurs vont, au contraire, dire qu’en géométrie elliptique il n’y a pas de symétries orthogonales mais au contraire que des rotations, ce qui est un point de vue tout à fait correct en terme de structures.
Manipulation de la figure suivante
\(A\) et \(M\) se manipulent à la fois par \(u_A\) et \(u_M\) pour les laltitudes de leurs parallèles respectives, et directement sur leurs parallèles. Quand \(u_A\) est au dessus de \(O\), \(A\) est dans l’hémisphère nord, donc le projeté est celui de \(sA\) son symétrique dans l’hémisphère sud. De même pour le symétrique de \(A, symA\), par rapport à la polaire de \(M\).
Déplacer \(A\), par \(A\) et/ou \(u_A\) de même l’axe de symétrie par son pôle \(M\). Observer le passage quand \(symAell\)passe par l’équateur.
Ne pas hésiter à déplacer le repère par un clic-glissé ou un doigt-glissé.
Remarque : N’ayant pas l’outil arc de cercle en 3D (en fait des arcs d’ellipse), on est amené à tracer les cercles entiers dans le plan du sol.
Le passage au plan est élémentaire : on applique la macro « Point elliptique » à l’inverse de \(M\) par rapport à la droite \((AB)\). C’est intéressant de voir les trois points de vue : intrinsèquement elliptique, mais aussi du point de vue de la symétrie axiale et celui de la symétrie centrale.
Une caractérisation algébrique de la géométrie elliptique
Revenons sur les triangles tripolaires, L’existence d’un tel triangle est une caractérisation de la géométrie elliptique.
Mais puisqu’elle est illustrée dans un modèle, cette configuration peut paraître affaiblie pour parler d’une caractérisation. Pourtant, du point de vue d’une axiomatique construite sur les symétries orthogonales, cette propriété est structurelle. Voici le raisonnement depuis l’existence d’un triangle tripolaire.
Soit donc \(ABC\) un triangle tripolaire et \(a, b, c\), les polaires des sommets respectifs. On note \(s_x\) la symétrie orthogonales par rapport à la droite \(x\) et \(s_X\) la symétrie centrale par rapport au point \(X\). Par des propriétés algébriques sur les éléments d’ordre 2, comme les droites \(a\) et \(b\) sont orthogonales, le produit \(s_a o s_b\) est un élément d’ordre 2 qui laisse le point d’intersection \(C\) invariant. Ce produit est donc la symétrie centrale \(s_C\). On a donc \(s_a o s_b=s_C=s_c\), soit \(s_a o s_b o s_c = Id\).
Ce sera, en fait, une caractérisation de cette géométrie qui, sous une forme plus algébrique, dans un langage de groupe, s’exprime sous la forme : Il existe trois droites a, b et c telles que abc=1.
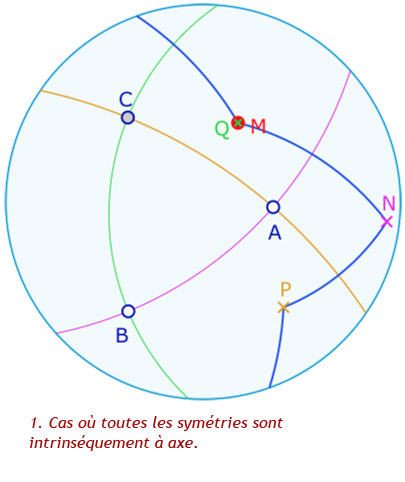
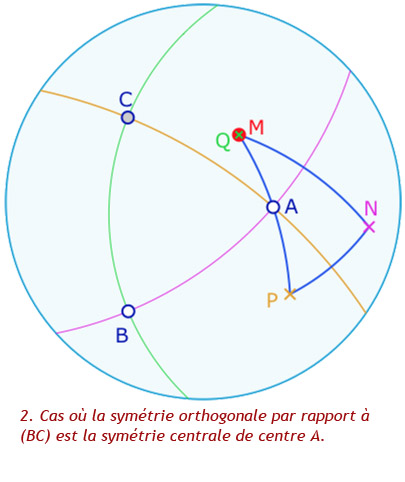
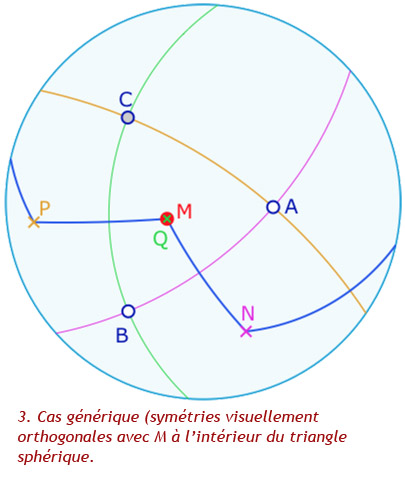
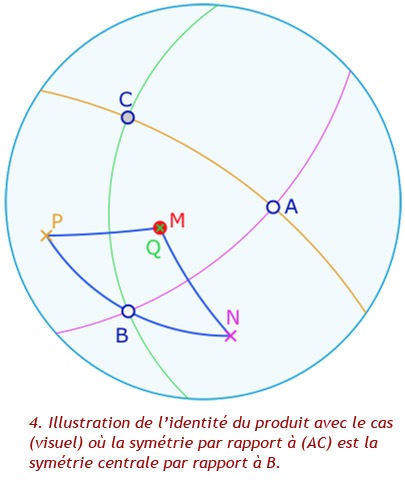
Dans la galerie ci-dessous quelques exemple commentés de ce que l’on peut réaliser à la figure suivante.
On a \(N=s_{(AB)}(M)=s_c(M)\), \(P=s_{(AC)}(N)=s_b(N)=s_b o s_c(M)\) et \(Q=s_{(BC)}(P)=s_a(P)=s_a o s_b o s_c(M)\).
Alors \(Q=M\), soit \(s_a o s_b o s_c = Id\).
La figure correspondante
Dans cette figure, on peut agir sur \(A\) et \(B\) et sur le point \(M\).