Rappel du contexte (repris de la page d’introduction aux droites de Hilbert)
Hilbert considère le modèle de la géométrie euclidienne plane suivant. Il se donne l’ellipse centrée à l’origine du repère canonique, de grand axe 1 et de petit axe 1/2. Soit l’ellipse d’équation \(x^2+4y^2=1\). Puis il considère le point \(F \displaystyle \left( \frac{3}{2},0 \right)\) et montre que tout cercle passant par \(F\) et coupant l’ellipse, soit est tangent à l’ellipse, soit ne coupe l’ellipse qu’en deux points distincts. Plus précisément il montre que tout cercle coupant l’ellipse en 4 points ne passe pas par \(F\). Cela lui permet de définir une nouvelle géométrie de la façon suivante :
Droites et segments
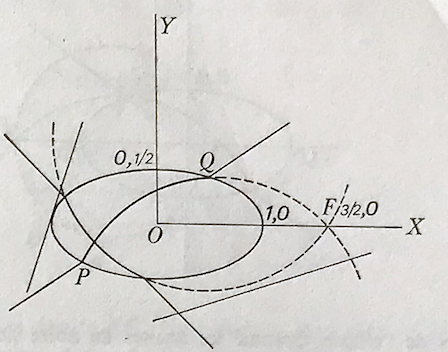
«Élaborons notre nouvelle géométrie comme suit. Comme points prenons les points du plan \(xy\). Comme droites, choisissons, sans modification, celles du plan qui ne coupent pas l’ellipse ou qui lui sont tangentes; par contre si une droite \(g\) coupe l’ellipse en deux points \(P\) et \(Q\), construisons le cercle passant par \(P\), \(Q\) et \(F\). Ce cercle ne coupe pas l’ellipse hors de ces points. Sur la droite \(g\) remplaçons le segment compris entre \(P\) et \(Q\) par l’arc du cercle précédent situé à l’intérieur de l’ellipse. Les deux demi-droites portées par \(g\) limitées à \(P\) et \(Q\) et l’arc de cercle ci-dessus constituent une droite de notre nouvelle géométrie(*). Supposons la construction effectuée pour toutes les droites du plan. Les droites de la nouvelle géométrie satisfont les axiomes (I.1 et I.2) et (IV). Les axiomes (II) sont aussi valables en considérant l’ordre naturel des points sur ces droites. Nous dirons que deux segments \(AB\) et \(A’B’\) sont congruents si les segments \(AB\) et \(A’B’\) mesurés éventuellement en tout ou partie sur un arc de cercle ont des longueurs habituelles égales. »
(*) On parle, dans ce contexte, de H-droite, pour droite de Hilbert, et de H-segment.
En géométrie dynamique, une droite de base est définie par deux points, la construction de telles H-droites nécessite de distinguer trois cas :
• Cas 1 : les deux points sont extérieurs à l’ellipse.
• Cas 2 : les deux points sont intérieurs à l’ellipse.
• Cas 3 : un des points est à l’intérieur, l’autre à l’extérieur.
Un traitement spécifique est nécessaire pour chacun de des trois cas, le troisième étant nettement plus complexe que les deux premiers, eux, triviaux.
Traitement dynamique des cas 1 et 2
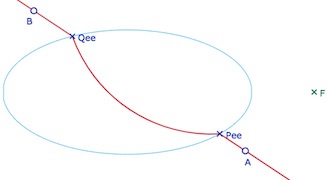
Ces deux premiers cas relèvent d’une simple construction géométrique, mais en géométrie dynamique, il y a souvent des ajustements à faire. Pour le premier cas, il s’agit simplement de l’intersection d’une droite et d’une ellipse. C’est tout-à-fait immédiat. On note \(P_{ee}, Q_{ee}\) ces deux points, le suffixe \({ee}\) pour signifier que les deux points de base sont extérieurs à l’ellipse. Le second cas consiste ensuite à construire les points d’intersection \(P_{ii}, Q_{ii}\), les intersections de l’ellipse et de la droite de Hilbert quand les deux points de base sont à l’intérieur. Il y a alors un premier traitement à effectuer.
Pour obtenir les intersection d’un cercle et d’une ellipse, on transforme le cercle en conique passant par 5 points pour récupérer la gestion automatique des intersections des coniques. Ainsi, si ce cercle dynamique – noté \(QuadF\) dans le code ci-dessous – coupe l’ellipse fixe \(Hell\) en deux points seulement, dynamiquement, ces deux points ne sont pas toujours les mêmes, ils dépendent, entre autres, de l’orientation du cercle. En fait c’est une conséquence de l’incompatibilité entre la continuité des intersections et le déterminisme des figures comme cela a déjà été présenté ici.
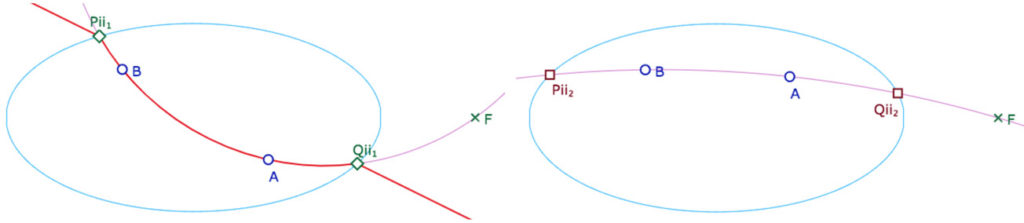
On commence par déclarer les 4 points d’intersection entre les deux coniques \(Hell\) et \(QuadF\). Les logiciels de géométrie dynamique contemporains permettent d’avoir accès aux intersections tels qu’elles sont codées en interne dans le logiciel.
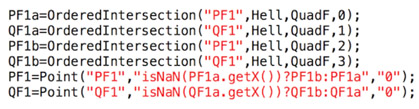
En pratique, il s’agit de choisir entre deux paires d’intersection (ce qui est plus simple). Le tout est ensuite placé dans une macro, et devient transparent à l’utilisation (les noms proposés ici sont différents de la figure car ils sont dans une macro plus générique).
Manipulation dynamique de cette construction
Dans la figure illustrée ci-dessous, figure à ouvrir dans un nouvel onglet, on a volontairement construit une seule partie de la construction pour voir le problème.
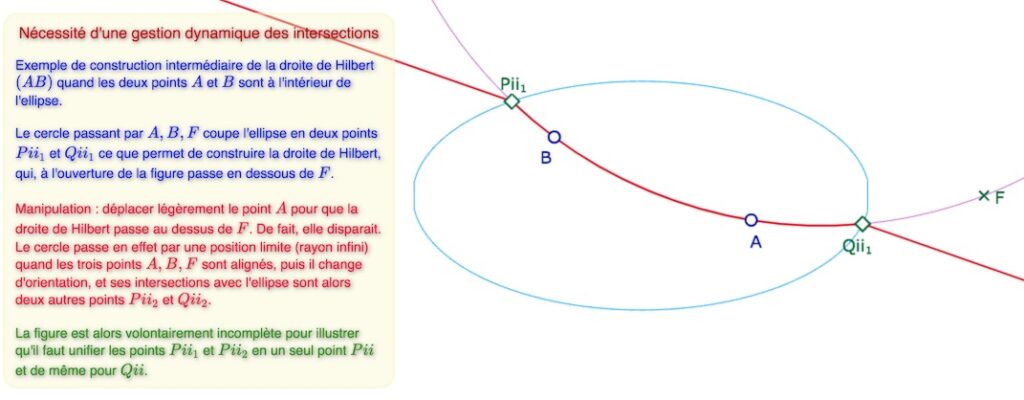
En faisant glisser \(A\) pour que la H-droite passe au dessus \(F\), observer ce qu’il se passe, puis poursuivre \(A\) vers le haut en restant dans l’ellipse, on voit la H-droite se reconstruire : la gestion interne des noms des intersections est plus complexe que la simple orientation du cercle.
Réalisation algébrique du cas 3
Le troisième cas (construction des points \(P_{ie}, Q_{ie}\), pour un point de base de la droite intérieur l’autre extérieur) qui pourtant n’est a priori qu’un problème du 4° degré, est nettement moins trivial à traiter. Dans une première mise en ligne (décembre 2021), ce troisième cas a fait l’objet d’une démarche particulière, en programmation Blockly, approche que l’on a conservé en archive. L’objectif de cet article est de détailler la réalisation d’une construction algébrique, avec les formules de résolution de ce problème d’ordre 4.
Une approche originale – Un premier résultat
C’est l’article de Bernard Parisse, (février 2024) sur la comparaison entre Xcas et AlphaGeometry (IA de Google pour la géométrie) qui m’a motivé à reprendre cette question, abandonnée il y a quelques années, avec la démarche de programmation par approximation successive de la première mise en ligne du menu Non Arg de ce site. A l’époque, avec mon collègue Dominique Tournès, nous cherchions le centre du cercle solution, mais c’était assez inextricable et le calcul formel ne produisait pas quelque chose d’utilisable.
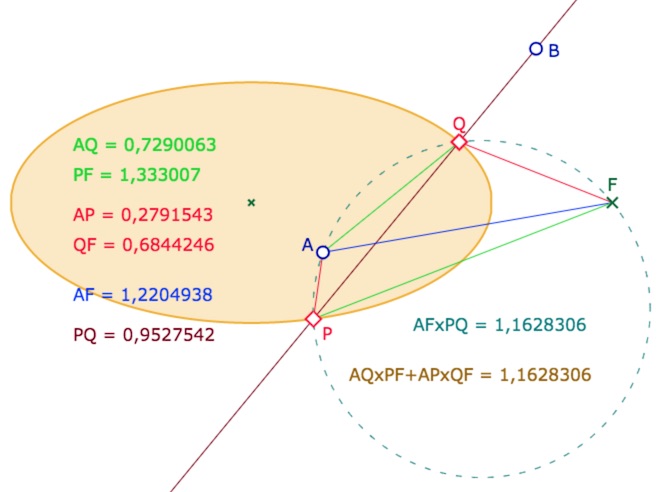
Dominique s’est alors emparé à nouveau du problème, en prenant soin de chercher à l’aborder autrement : au lieu de chercher le centre du cercle passant par \(A\) et \(F\) tel que \(B, Q, P\) soient alignés, il considère une droite de la forme \(a(X-x_B)+ Y-y_B=0\), où \(B(x_B,y_B)\). On calcule facilement ses intersections \(P\) et \(Q\) avec l’ellipse. L’approche originale de Dominique consiste à déterminer le coefficient \(a\) tel que les 4 points \(P, A, Q, F\) soient cocycliques en utilisant le théorème de Ptolémée \(AF \times PQ = AQ \times PF + AP \times QF\).
En pratique, pour éviter des calculs, à nouveau inextricables avec les racines carrés, Dominique transforme la condition de cocyclicité sous la forme \((AF^2.PQ^2-AQ^2.PF^2-AP^2.QF^2)^2 = 4PF^2.AQ^2AP^2.QF^2\), en élevant deux fois au carré, même si on perd assurément « quelque chose » dans ces élévations au carré.
On a donc le résultat avec les formules de Cardan, en particulier avec des racines carrées et des racines cubiques. L’expression de \(a\) produite par Mathematica fait plus de 19000 caractères mais une expression de plus de 3300 caractères intervient 4 fois. Cette expression, une fois extraite, se factorise en 1146 caractères seulement.
-4(128yA^6yB(9(3-2xB)^2+16yB^2)+48yA^4yB(-1297+72xA^2(3-2xB)^2+3105xB-6xA(-3+2xB)(-35+9xB(1+xB))-3xB^2(901+6xB(-57+8xB))+36yB^2+8(xA(-27+16xA-6xB)+9xB)yB^2)+(-3+2xA)^3yB(9(-1-3(-2+xB)xB+xA(-6+4xB))(3+3(8-3xB)xB+8xA^2(-3+2xB)+xA(-34-6(-5+xB)xB))+4(3+2xA-3xB)(45+32xA^2-9(-2+xB)xB+6xA(-11+2xB))yB^2)+4yA^3(4906-11205xB+9(-8xA^2(3-2xB)^2(-7+3(-3+xB)xB)+2xA(-3+2xB)(136+3xB(39+xB(-35+3(-3+xB)xB)))+xB^2(2519+3xB(-903+xB(433-90xB+8xB^2))))+7560yB^2+60(8xA^2(29+12(-3+xB)xB)+9xB(1+3xB(-5+2xB))-6xA(72+xB(-71+9xB+6xB^2)))yB^2)-3(3-2xA)^2yA(3(-1-3(-2+xB)xB+xA(-6+4xB))(-17+2xA(-3+2xB)(-7+3(-3+xB)xB)+3xB(-2+xB(-7+6xB)))-4(20xA^2(29+12(-3+xB)xB)-30xA(14+xB-15xB^2+6xB^3)+9(41+xB(-41+xB(31+3xB(-7+2xB)))))yB^2)+48yA^5(189+580yB^2-3(-3+xB)xB(-1+12(-3+xB)xB-80yB^2))+12(-3+2xA)yA^2yB(16xA^3(9(3-2xB)^2+16yB^2)+3(344+7xB-615xB^2+561xB^3-225xB^4+36xB^5+36(2+(-5+xB)xB)yB^2)-24xA^2(4(6+5yB^2)+xB(11+9xB(-5+2xB)+8yB^2))+2xA(-1786+3xB(1209-925xB+315xB^2-39xB^3-12(-9+xB)*yB^2))))
Expression nommée « coef » dans la figure
Après quelques autres repérages d’expressions communes, on arrive aux simplifications suivantes. On peut écrire l’expression de \(a\) sous forme d’une somme \(a=U-V+W\) avec
Expression de U
-((2(8yA-9xByA+3xB^2yA-9yB+4xA^2yB+9xByB-6xAxByB+4yA^2yB))/(3(3+16xA-12xA^2-18xB+8xA^2xB+9xB^2-6xAxB^2-12yA^2+8xByA^2)))
Pour V et W on note
coef2
(-16(8yA-9xByA+3xB^2yA-9yB+4xA^2yB+9xByB-6xAxByB+4yA^2yB)^2+6(3+16xA-12xA^2-18xB+8xA^2xB+9xB^2-6xAxB^2-12yA^2+8xByA^2)(6+5xA-6xA^2-9xB+4xA^2xB-6yA^2+4xByA^2-36yAyB+24xByAyB+18yB^2-12xA*yB^2))
et expVW = (coef^2+4*coef2^3)
Expression de V
coef2/(32^(2/3)(3+16xA-12xA^2-18xB+8xA^2xB+9xB^2-6xAxB^2-12yA^2+8xByA^2)(coef+sqrt(expVW))^(1/3))
Expression de W
(coef+sqrt(expVW))^(1/3)/(62^(1/3)(3+16xA-12xA^2-18xB+8xA^2xB+9xB^2-6xAxB^2-12yA^2+8xB*yA^2))
Quelques simplifications pour l’expression de \(a=U-V+W\)
Figure dynamique quand les trois nombres \(\mathbf{U, V, W}\) existent
Commençons par une première figure de travail, pour illustrer, déjà, que la démarche aboutit, mais surtout pour mieux situer les questions à résoudre.
Déplacer \(A\) ou \(B\) en conservant \(B\) à l’extérieur de l’ellipse et \(A\) à l’intérieur.
La droite disparaît quand \(expVW<0\) ou quand \()coef+\sqrt{expVW})<0\) car ces cas ne sont pas encore traités.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet. Dans tous les cas, penser à éloigner \(B\) de l’ellipse pour rendre \(expVW<0\), comme ci-dessous.

Une figure plus générique
L’expression \(coef+\sqrt{expVW}\) est un nombre réel si \(expVW>0\) et un nombre complexe si \(expVW<0\). Le traitement de la racine cubique n’est pas le même.
Quand l’expression est un nombre complexe, DGPad renvoie, naturellement, une liste de trois racines cubiques de ce nombre complexe. Ce qui va aboutir à trois solutions pour le nombre \(a\). On retrouve ici la question soulevée de la double évolution au carré dans le théorème de Ptolémée. En effet, cette double élévation au carré contient finalement les trois quadrilatères que l’on peut obtenir avec les 4 points \(P, A, Q, F\) où les diagonales deviennent des côtés et réciproquement.
La démarche retenue est de remarquer (après les calculs des trois solutions avec Mathematica) que si \(a_1=U-V+W\) est une solution réelle (ie \(V\) et \(W\) réels) les deux autres solutions sont \(a_2=U-j^2V+jW\) et \(a_3=U-jV+j^2W\) … quand ces deux nombres sont eux aussi des réels, où \(j\) est la racine cubique de l’unité \(\displaystyle j=-1+\frac{\sqrt{3}}{2}\), et \(j^2=-1-j\).
En fait ces trois valeurs \(a_1, a_2, a_3\), quand elles sont réelles, produisent trois droites, dont une seule coupe l’ellipse.
Dans un premier temps, on va commencer par mettre cette démarche en place, toujours avec \(B\) à l’extérieur de l’ellipse et \(A\) à l’intérieur. Dans une étape suivante, on étendra l’aspect dynamique de la figure, où \(A\) et \(B\) peuvent échanger leurs rôles, en reprenant les choses de manière plus compacte pour une transformation en macro-construction avec le moins d’objets crées. Dans une dernière section, on ajoutera à ce « cas 3 » de traitement algébrique, les deux cas géométriques, pour avoir une macro qui renvoie une droite générale dans tous les cas.
Prendre la racine cubique d’un nombre et d’un point en même temps
Tout d’abord, on simplifie encore un peu l’écriture en définissant deux nouvelles expressions
coefV = 32^(2/3)(3+16xA-12xA^2-18xB+8xA^2xB+9xB^2-6xAxB^2-12yA^2+8xB*yA^2)
et
coefW =62^(1/3)(3+16xA-12xA^2-18xB+8xA^2xB+9xB^2-6xAxB^2-12yA^2+8xB*yA^2)
Pour DGPad, un nombre complexe est un point. Pour prendre la racine cubique d’une expression qui peut être soit d’un nombre réel soit un nombre complexe, on transforme le nombre réel en un complexe de partie imaginaire nulle.
Pour prendre la racine cubique de (coef+sqrt(expVW))
on définit la variable (qui est alors une liste)
LesR3 = (expVW>0)?[coef+sqrt(expVW),0]^(1/3):[coef,sqrt(-expVW)]^(1/3)
Les nombres \(a_1, a_2, a_3\) s’écrivent alors (avec le préfixe « exp » pour rappeler que ce sont des points, et pas des nombres réels).
expa1 = U-(coef2/coefV)/LesR3[0]+LesR3[0]/coefW
expa2 = U-[-0.5,sqrt(3)/2](coef2/coefV)/LesR3[0]+[-0.5,-sqrt(3)/2]LesR3[0]/coefW
expa3 = U-[-0.5,-sqrt(3)/2](coef2/coefV)/LesR3[0]+[-0.5,sqrt(3)/2]LesR3[0]/coefW
On a directement écrit les points représentant \(j\) et \(j^2\) pour éviter que ces variables soient reconstruites à chaque macro. De même on présente ici séparément les trois nombres complexes \(expa_1, expa_2, expa_3\), mais dans une version plus compacte, on pourra les regrouper dans une liste.
Reste à construire ces trois droites quand les parties imaginaires des expressions ci-dessus sont nulles. Dans la première version de travail présentée au dessus on utilisait le point de la droite d’abscisse nulle, soit le point \([0,ax_B+y_B]\). Ici, comme on veut ne construire la droite que si le point correspond à un nombre réel, on utilise une expression du type
(abs(expa1[1])<0.001)?[0,expa1[0]*xB+yB]:[NaN,NaN]
Le point Ptdr1 ci-dessous, on fait de même pour Ptdr2 et Ptdr3
On ne teste pas directement l’égalité à 0 d’un nombre réel en JavaScript … même avec Mathematica, quand on teste des valeurs numériques, on n’obtient pas des réels mais des nombres complexes avec une partie imaginaire de l’ordre de \(10^{-16}\) ce qui relève, là aussi, de l’erreur d’arrondi.
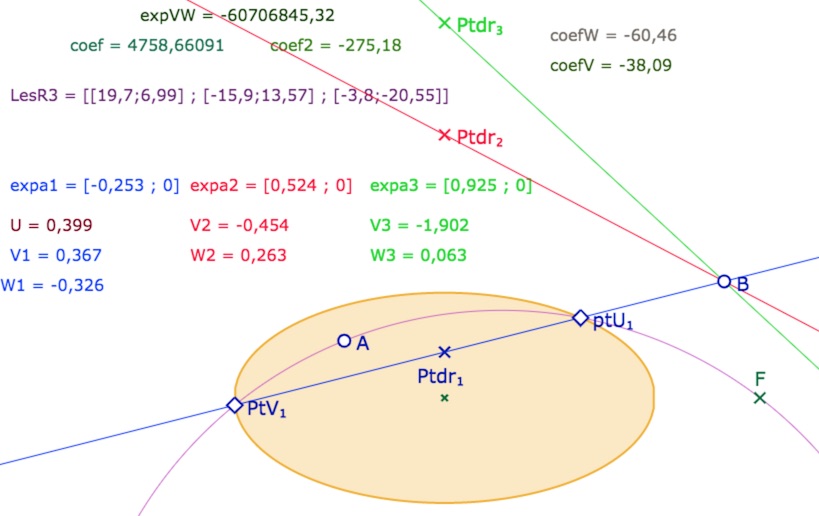
Voici une configuration où les trois nombres complexes sont bien des nombres réels et où les trois droites, pour chacune des trois racines, existent, mais une seule coupe l’ellipse, celle correspondant à \(expa_1\).
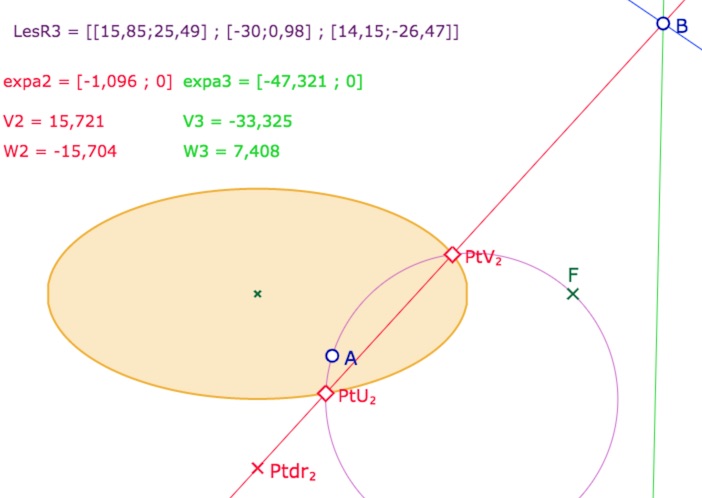
Voici une autre configuration avec, là encore l’existence des trois droites, mais où c’est la droite correspondant à \(expa_2\) qui coupe l’ellipse.
Avant de ne conserver que la droite qui coupe l’ellipse, cela peut être intéressant de manipuler cette figure intermédiaire où l’on voit (assez rarement) les trois droites en même temps :
Lancer cette nouvelle figure de travail dans un nouvel onglet.
Rappel : \(\mathbf{B}\) reste à l’extérieur de l’ellipse et \(\mathbf{A}\) à l’intérieur.
Dans la configuration illustrée ci-dessus, en rapprochant \(B\) de \(A\) en conservant la même pente, la droite solution devient rapidement la bleue, la rouge et la verte se rapprochent jusqu’à disparaître …
Construire la H-droite (AB)
Dans un premier temps, on transforme ce qui précède en une vraie droite de Hilbert. Pour cela il suffit de faire la construction géométrique basée sur les points d’intersections de la droite avec l’ellipse, par exemple à partir du milieu de ces deux points. On garde encore, temporairement, les trois droites des trois couleurs.
On peut aussi préférer ouvrir cette figure – plus grande – dans un nouvel onglet.
Remplacer ces trois droites par une seule
Il suffit de construire les points \(U_{ie}\) de \(V_{ie}\) suivants, et construire l’unique droite de Hilbert passant par \(A\) et \(B\) à partir de ces deux points.
Uie = isNaN(PtU1.getX())?(isNaN(PtU2.getX())?PtU3:PtU2):PtU1
Vie = isNaN(PtV1.getX())?(isNaN(PtV2.getX())?PtV3:PtV2):PtV1
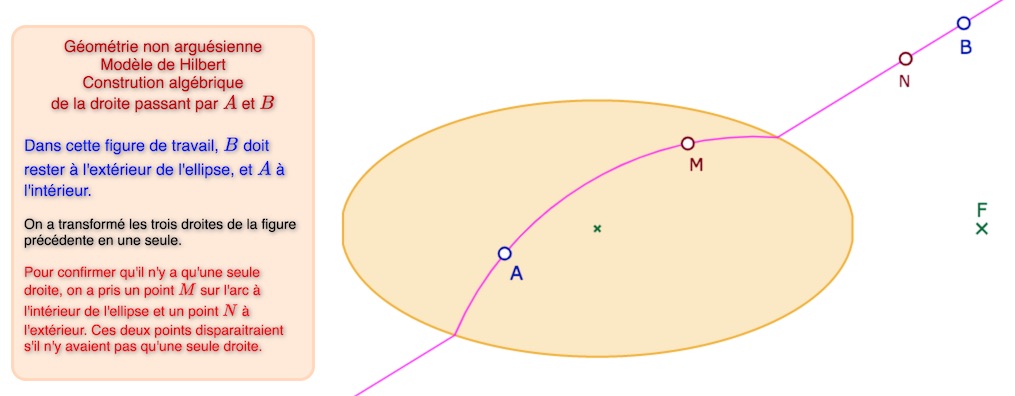
Ouvrir cette nouvelle figure dans un autre onglet.
Construction finale
Dans cette section, on commence par généraliser ce qui précède en permettant d’inverser les deux points \(A\) et \(B\) dans la manipulation de la figure, puis dans un dernier paragraphe, on ajoutera les deux cas géométriques.
Inversion des points \(\mathbf{A}\) et \(\mathbf{B}\)
Il s’agit de transformer ce qui précède tout en permettant que \(B\) soit aussi à l’intérieur et, alors, \(A\) à l’extérieur, ceci sans tout réécrire – et en particulier en conservant l’expression algébrique \(coef\) assez lourde.
Pour conserver une seule expression \(coef\), il faut que \([x_A, y_A]\) puisse devenir (aussi) le point à l’intérieur, noté désormais \(ABint\), et, en même temps \([x_B, y_B]\) le point à l’extérieur, noté \(ABext\). Pour cela on introduit, comme pour les deux premiers cas géométriques, les deux booléens \(AExt = x_A^2+4y_A^2<1\) et de même, \(BExt\) pour le point \(B\). Les points \(ABint\) et \(ABext\) sont alors :
Nouveau A : le point ABint = [x(A)(AExt==0)+x(B)(BExt==0), y(A)(AExt==0)+y(B)(BExt==0)]
Nouveau B : le point ABext = [x(A)(AExt==1)+x(B)(BExt==1), y(A)(AExt==1)+y(B)(BExt==1)]
Avec ces points, on conserve les expressions \(coef, \, coef2, \; coefV, \; coefW\). Il reste à modifier les racines cubiques, et les nouveaux points des droites solutions, les points \(Ptdr_i\). En effet, les trois expressions \(expa_1, expa_2, expa_3\) restent identiques, elles sont plus génériques. La racine cubique est immédiate à adapter :
Nouvelles racines cubiques
(AExt+BExt==1)?((expVW>0)?[coef+sqrt(expVW),0]^(1/3):[coef,sqrt(-expVW)]^(1/3)):NaN
Pour les points des droites, on peut utiliser aussi bien les points \(ABint\) et \(ABext\) (avec leurs coordonnées \(x_A, y_A, x_B, y_B\) ou les points initiaux \(A\) et \(B\) avec leurs coordonnées propres \(x(A), y(A), x(B), y(B)\). Par exemple dans ce dernier cas, on choisit les points suivants :
(abs(expa1[1])<0.001)?[0,expa1[0](x(B)(BExt==1)+x(A)(AExt==1))+y(B)(BExt==1)+y(A)*(AExt==1)]:[NaN,NaN]
(abs(expa2[1])<0.001)?[0,expa2[0](x(B)(BExt==1)+x(A)(AExt==1))+y(B)(BExt==1)+y(A)*(AExt==1)]:[NaN,NaN]
(abs(expa3[1])<0.001)?[0,expa3[0](x(B)(BExt==1)+x(A)(AExt==1))+y(B)(BExt==1)+y(A)*(AExt==1)]:[NaN,NaN]
Pour passer des trois droites produites à une seule, on procède comme dans la section précédente, avec la création des points \(U_{ie}\) et \(V_{ie}\).
Échanger les positions de \(A\) et \(B\)
Préférer ouvrir cette figure plus grande dans un nouvel onglet (où on voit aussi le point \(F\)).
Ajout des deux cas géométriques
Cette partie est très simple si on s’inspire de ce qui a été fait précédemment. L’idée est d’ajouter aux points \(U_{ie}\) et \(V_{ie}\) – qui n’existent que si \(AExt+BExt=1\) – les points \(U_{ii}\) et \(V_{ii}\) (le suffixe \(_{ii}\) signifiant que les deux points \(A\) et \(B\) sont intérieurs à l’ellipse), en faisant en sorte qu’ils n’existent que si \(AExt+BExt=0\) et les points \(U_{ee}\) et \(V_{ee}\), quand les deux points \(A\) et \(B\) sont extérieurs à l’ellipse, soit \(AExt+BExt=2\).
Le logiciel ne traitant pas l’intersection d’un cercle et d’une conique, pour le cas \(U_{ii}\) et \(V_{ii}\), on transforme le cercle en une ellipse passant par 5 points et on peut prendre l’intersection des deux ellipses (traitement spécifique déjà abordé dans cette page). On écrit par exemple :
Pour Uii : (AExt+BExt==0)?PF11:NaN si PF11 est un des points de l’intersection du cercle ellipse et de l’ellipse de référence
Pour Uee : (AExt+BExt==2)?Pe:NaN si Pe est un des points de l’intersection de la droite affine (AB) avec l’ellipse de référence.
Et bien entendu, ces points d’intersections de l’ellipse avec les 3 cas de droites étant construits, on les unifie par un classique
Ugg = isNaN(Uie.getX())?(isNaN(Uee.getX())?Uii:Uee):Uie
Vgg = isNaN(Vie.getX())?(isNaN(Vee.getX())?Vii:Vee):Vie
Toutefois, selon l’orientation de la droite, les points \(U_{gg}\) et \(V_{gg}\) peuvent s’échanger. Si cela est sans importance pour un dessin, pour une figure dynamique, en particulier quand on va ajouter un point sur la droite, cela peut provoquer de la discontinuité dans la figure, car les points seront – in fine – gérés par une barycentration vis à vis de ces deux points. On ajoute donc une couche supplémentaire avec deux points, que l’on nomme ci-dessous \(P_h\) \(Q_b\), \(P_h\) étant celui des deux (entre \(U_{gg}\) et \(V_{gg}\)) qui a l’ordonnée la plus grande. Il y a donc une demi-droite orientée vers « le haut » (de l’écran) \(R_h\) (R par Ray) et une orientée vers « le bas » \(R_b\).
Les points \(Exh, Exb\) et \(CtrArchb\) sont renvoyés (en plus) par la macro
Droite Hilbert Details qui servira pour pouvoir déplacer un point sur une H-droite.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet
Si vous savez utiliser l’interface du logiciel, dans cette dernière figure (celle ouverte dans un autre onglet), ajouter un point \(C\) à la figure et avec la macro Droite Hilbert F Hell AB, construire les droites \((AC)\) et \((BC)\) en montrant successivement le point \(F\), l’ellipse de référence et les deux points de la droite. Vous avez ainsi construit un triangle générique dans le modèle non arguésien de Hilbert.
Remarque sur l’application de la macro : pour que la droite affine \((AB)\) disparaisse quand elle n’est pas une droite de Hilbert, il y a une gestion de son apparition qui doit être dans la macro. Il apparaît donc – comme dans d’autres macros de ce site – une expression qui gère se point. Il suffit de le cacher (outil gomme) et surtout pas le supprimer (icone corbeille).
Le menu « Non Arg » sera peu à peu repris en tenant compte de cette réalisation …
Traitement algébrique de l’orthogonalité à une droite
« De l’orthogonalité », car il n’y a pas toujours de perpendiculaire à une droite issue d’un point, et il peut exister jusqu’à trois perpendiculaires à une droite, comme ci-dessous : deux hilbertiennes et une euclidienne.
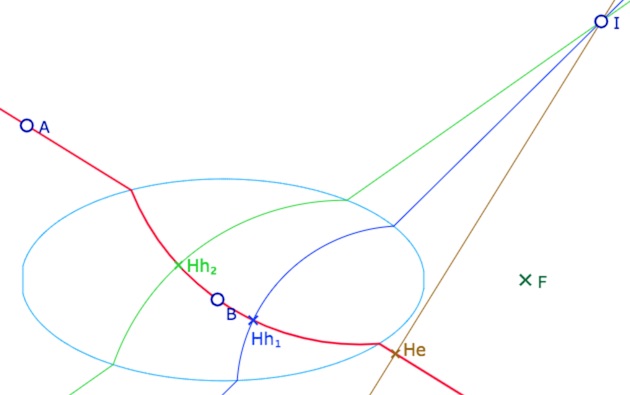
Principe de la démarche
C’est encore Dominique qui a cherché les solutions génériques avec Mathematica. On s’intéresse dans un premier temps au seul cas délicat, celui d’une droite \((AB)\) qui coupe l’ellipse et d’un point \(I\) extérieur à l’ellipse. On cherche les deux droites vertes et bleues ci-dessus, avec leurs arcs de cercle orthogonaux à celui de la droite \((AB)\), le point \(I\) étant aligné avec les deux intersections de ces arcs avec l’ellipse.
La droite \((AB)\) étant construite, on a les coordonnées du centre de l’arc de cercle, que l’on nomme \(CtrArc_{AB}\) de coordonnées \((x_C, y_C)\). C’est considéré comme une donnée initiale. On note \((x_I, y_I)\) les coordonnées du point \(I\). On cherche, comme dans le cas de la droite, le coefficient \(a\) d’e la’une droite \(y = y_I + a(x-x_I)\) qui coupe l’ellipse en deux points \(P\) et \(Q\) dont on calcule les coordonnées. On calcule ensuite les coordonnées de \(CtrOrtho\) le centre du cercle circonscrit à \(F, P, Q\). L’orthogonalité se traduit par la recherche de \(a\) tel que les droites \((F \, CtrOrto)\) et \((F \, CtrArc_{AB})\) soient orthogonales.
Les résultats
La structure de la solution est assez proche de celle de la droite, puisque justement, on cherche une droite de Hilbert. On ira donc nettement plus vite. On nomme, avec le préfixe \(p\), les expressions analogues au cas de la droite. On a alors
pCoef factorisé (beaucoup plus compact que celui de la droite)
-32(32(8+3(-3+xI)xI)^3yC^3+72(-3+2xC)(8+3(-3+xI)xI)(-26+xI(64-39xI+6xI^2))yC^2yI+27(-3+2xC)^3yI(340-758xI+582xI^2-177xI^3+18xI^4+4(4+xI(6+(-6+xI)xI))yI^2)+9(3-2xC)^2yC(460+1392yI^2+3xI(-74+3(-2+xI)xI(71+2xI(-29+6xI))-904yI^2+4xI(166-51xI+6xI^2)*yI^2)))
pCoefU=-30+20xC+36xI-24xCxI-9xI^2+6xC*xI^2
pU=-(2(8yC-9xIyC+3xI^2yC-18yI+12xCyI+9xIyI-6xCxIyI))/(3*pCoefU)
pCoefV=(-64(8yC-9xIyC+3xI^2yC-18yI+12xCyI+9xIyI-6xCxIyI)^2+12(-30+20xC+36xI-24xCxI-9xI^2+6xCxI^2)(-39+26xC+36xI-24xCxI+72yCyI-48xIyCyI-36yI^2+24xC*yI^2))
pV =-pCoefV/(6*2^(2/3)pCoefU(pCoef+sqrt(pCoef^2+4pCoefV^3))^(1/3))
pW = (pCoef+sqrt(pCoef^2+4pCoefV^3))^(1/3)/(12*2^(1/3)*pCoefU)
La solution réelle est ap1=pU+pv+pW quand celle-ci existe.
Mais comme il y a des racines cubiques complexes – les autres solutions \(ap2, ap3\) font directement intervenir les nombres complexes \(j\) et\(j^2\) comme pour la droite algébrique – on reprend la démarche utilisée pour les droites. On nomme donc, à nouveau :
exppVW=pCoef^2+4*pCoefV^3
LespR3=(exppVW>0)?[pCoef+sqrt(exppVW),0]^(1/3):[pCoef,sqrt(-exppVW)]^(1/3)
______________ Les nouveaux ap1, ap2, ap3
expap1= pU-pCoefV/(6*2^(2/3)*pCoefU*LespR3[0])+LespR3[0]/(12*2^(1/3)*pCoefU)
expap2= pU-[-0.5,sqrt(3)/2]*pCoefV/(6*2^(2/3)*pCoefU*LespR3[0])+[-0.5,-sqrt(3)/2]*LespR3[0]/(12*2^(1/3)*pCoefU)
expap3= pU-[-0.5,-sqrt(3)/2]*pCoefV/(6*2^(2/3)*pCoefU*LespR3[0])+[-0.5,sqrt(3)/2]*LespR3[0]/(12*2^(1/3)*pCoefU)
On construit un point de la droite si le nombre est réel
(abs(expap1[1])<0.001)?[xI-1,yI-expap1[0]]:NaN
(abs(expap2[1])<0.001)?[xI-1,yI-expap2[0]]:NaN
(abs(expap3[1])<0.001)?[xI-1,yI-expap3[0]]:NaN
Tout cela fonctionne parfaitement bien. Dans la figure suivante, les trois droites sont bleue, rose et verte. On a ajouté le cas de la droite euclidienne (en marron) qui parfois peut couper aussi l’ellipse.
Figure de travail temporaire qui n’est correcte que pour \(I\) extérieur à l’ellipse
Déplacer le point \(I\) pour voir, par exemple que les solutions peuvent « changer de couleur »
Préférer ouvrir cette figure dans un nouvel onglet
Ajout du cas où le point \(I\) est intérieur à l’ellipse.
Quand la droite \((AB)\) coupe l’ellipse, il y a deux cas, l’intersection intérieure à l’ellipse – intersection de deux arcs de cercle – et l’intersection euclidienne, où le pied de la hauteur est extérieure à ‘ellipse.
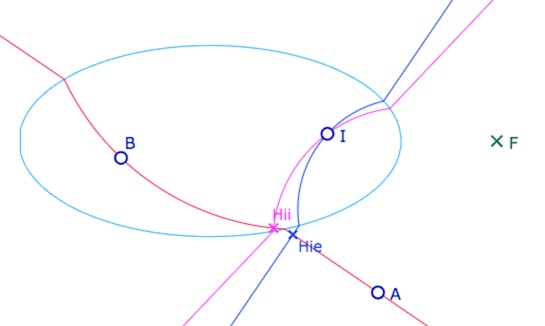
Mais il faut ajouter aussi le cas où le point \(I\) est intérieur à l’ellipse et la droite \((AB)\) extérieure. On utilise alors simplement le coefficient d’une droite orthogonale à une droite parallèle, la construction d’une parallèle est présentée dans cet autre article.
En étant un peu rapide, le coefficient principal est
bOrth
-(1/(12(pOrth(-3+2xI)+2yI)))(-9-36pOrth^2+4xI^2+16pOrth^2xI^2+36pOrthyI+4yI^2+16pOrth^2yI^2+sqrt((-9+4xI^2+36pOrthyI+4yI^2+4pOrth^2(-9+4 xI^2+4 yI^2))^2-24(pOrth(-3+2xI)+2yI)(5yI+32pOrth^2yI+pOrth(-6-5xI+6xI^2+6yI^2)+pOrth^3(-6-32xI+24xI^2+24yI^2))))
Mais il y a beaucoup de « sous cas », élémentaires, à traiter. Ainsi, au final la gestion de toutes ces droites orthogonales à la droite \((AB)\) se présente ainsi :
Hh1.setHidden(IExt==0);Hh2.setHidden(IExt==0);Hh3.setHidden(IExt==0);RH1h.setHidden(isNaN(Hh1.getX()) || IExt==0);RH1b.setHidden(isNaN(Hh1.getX()) || IExt==0 || IExt==0 || IExt==0);arcH1.setHidden(isNaN(Hh1.getX()) || IExt==0);RH2h.setHidden(isNaN(Hh2.getX()) || IExt==0);RH2b.setHidden(isNaN(Hh2.getX()) || IExt==0);arcH2.setHidden(isNaN(Hh2.getX()) || IExt==0);RH3h.setHidden(isNaN(Hh3.getX()) || IExt==0);RH3b.setHidden(isNaN(Hh3.getX()) || IExt==0 || IExt==0);arcH3.setHidden(isNaN(Hh3.getX()) || IExt==0);drtHe.setHidden(HeExt==0 ||isNaN(Heh.getX())==0 || IExt==0);RHeh.setHidden(HeExt==0 || IExt==0);RHeb.setHidden(HeExt==0 || IExt==0);arcHe.setHidden(HeExt==0 || IExt==0);He.setHidden(HeExt==0 || IExt==0 || IExt==0 || IExt==0 || IExt==0);RHeeh.setHidden(isNaN(Ph.getX())==0 || IExt==0);RHeeb.setHidden(isNaN(Ph.getX())==0 || IExt==0);arcHee.setHidden(isNaN(Ph.getX())==0 || IExt==0);Hee.setHidden(isNaN(Ph.getX())==0 || IExt==0);DrtHee.setHidden(isNaN(Ph.getX())==0 || isNaN(Peeh.getX())==0 || IExt==0);RIiih.setHidden(isNaN(Hii.getX()) || IExt==1);arcIii.setHidden(isNaN(Hii.getX()) || IExt==1);RIiib.setHidden(isNaN(Hii.getX()) || IExt==1);Hie.setHidden(IExt==1 ||HieExt==0);Rorthieh.setHidden(IExt==1 ||HieExt==0);Rorthieb.setHidden(IExt==1 ||HieExt==0);arcOrthie.setHidden(IExt==1 ||HieExt==0); »gestion des hauteurs »
La macro « Droite perpendiculaire » est nettement plus complexe que la macro « droite ». Par exemple, elle renvoie tous ces objets

On notera qu’il y a 7 pieds des hauteurs renvoyés alors qu’il n’y a que 6 droites. En fait les points \(H_e\) et \(H_{ee}\) sont un même point mais dans des contextes différents : gérer la nuance d’apparition d’un même point aurait été plus long que créer les deux points … c’est donc autant une solution d’efficacité qu’une solution de facilité …
Version finale de la perpendiculaire
On peut aussi déplacer l’ellipse en déplaçant la fenêtre au doigt ou à la souris.
Préférer ouvrir cette figure dans un nouvel onglet
La page sur l’orthogonalité du menu Non Arg montre des configurations où les trois pieds hilbertiens des perpendiculaires (\(Hh_1, Hh_2, Hh_3\) peuvent exister simultanément.
Les nouveaux développements possibles
Voici un triangle avec ses hauteurs. Il peut y en avoir 6, comme ci-dessous, avec 6 pieds des hauteurs. Le triangle est dans une configuration très proche d’un triangle biorthocentrique, avec deux orthocentres hybrides, celui de gauche à est 1/3 euclidien 2/3 hilbertien, celui de droite à 2/3 euclidien 1/3 hilbertien.
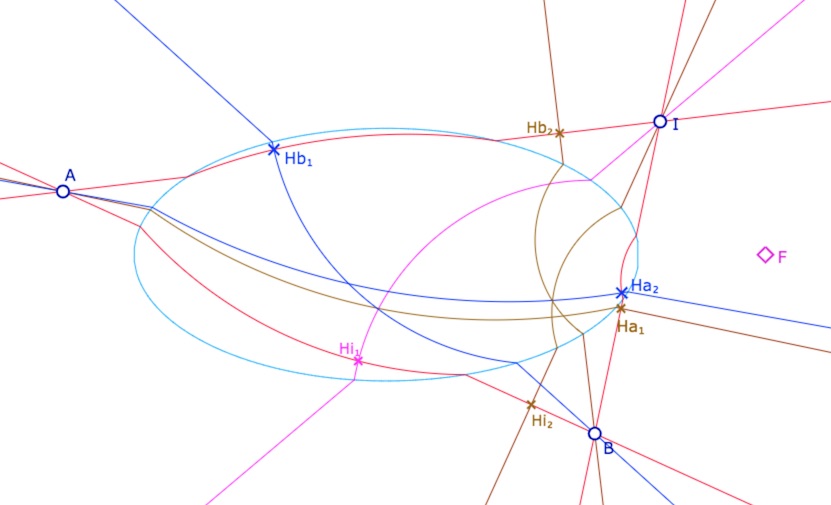
Ouvrir la figure associée dans un nouvel onglet.
De nouvelles pages du menu Non Arg abordent désormais les thèmes suivants en utilisant les nouvelles possibilités développées dans cet article :
• Les triangles orthocentriques
• Les triangles bi-orthocentriques
• Les triangles ayant à la fois un orthocentre et deux hauteurs parallèles.
Tous mes remerciements à Dominique Tournès sans qui tout ceci n’aurait pas été possible …