Contrairement aux autres pages sur les macros des différents modèles de géométries non euclidiennes, pour démystifier un peu cette géométrie si particulière qu’est la géométrie elliptique – une géométrie bornée, non orientable – après la section de présentation des macros et de leurs utilisations, on propose au lecteur le détail des constructions de plusieurs de ces macros. Il s’agit de montrer que ces objets, au comportement parfois surprenants (comme la symétrie orthogonale, le triangle elliptique), relèvent de constructions très simples.
On peut regarder rapidement les trois publications sur la géométrie elliptique de ce compte Instagram en lien avec ce site – publication « carrousel » de 10 images chacune – pour se remémorer quelques propriétés elliptiques.

Autre présentation rapide des GNE (via curvica974.re) sur le compte gne_dgpad
La liste des macro-constructions disponibles
Bien entendu, pour utiliser les macros de DGPad, il faut un peu de pratique de l’interface du logiciel. On a proposé des exemples euclidiens de manipulation dans cette page.
Les macros sont, classiquement, réparties en 5 dossiers : Points, Droites, Calculs, Cercles, Technique
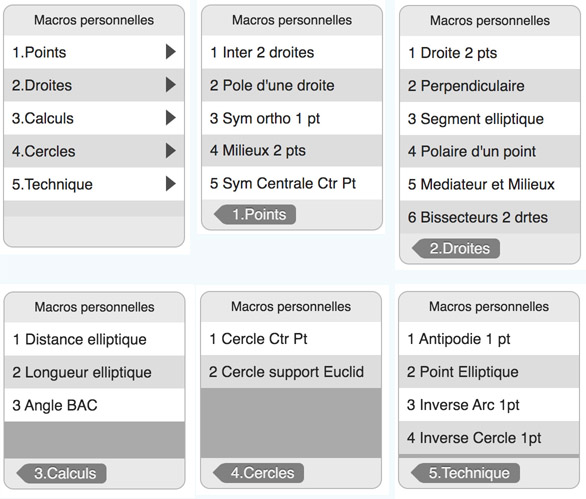
On rappel qu’a priori on ne voit que les quatre premières lignes de chaque dossier, il faut faire descendre la liste pour voir les suivantes.
Toutes les macros nécessitent comme premier objet le cercle du modèle … Toutes sauf bien entendu (on a l’habitude si on a manipulé les macros hyperboliques) celles d’inversion, les macros 3 et 4 du dossier Technique.
Le dossier Points
La macro Milieux construit, de manière cachée, pratiquement la même chose que la macro Médiateur (les deux médiatrices) et Milieux. Donc sauf si vraiment on ne doit pas utiliser de médiatrice, on lui préfèrera celle du dossier Droites pour éviter les doublons.
La symétrie centrale par rapport à un point n’est autre que la symétrie orthogonale par rapport à la polaire du point. Donc, comme ci-dessus, sauf illustration spécifique en présentation de la géométrie elliptique par exemple, on utilisera plutôt la symétrie orthogonale.
Le dossier Droites
On rappelle que l’attente d’un arc de cercle, dans la macro, est intitulée « cercle ».
La macro Bissecteur 2 drtes renvoie les deux bissectrices et les deux points bissecteurs. On n’a pas fait une macro « Points » spéciale pour deux points bissecteurs.
Le dossier Calculs
On y trouve seulement la distance entre deux points, la longueur « sur la sphère », et l’angle entre trois points. Là aussi, il faut donner en premier le cercle du modèle car ce cercle a un rayon modifiable, il n’est pas « de rayon 1 » comme dans les formules que l’on peut trouver dans les livres.
Le dossier Cercles
Comme il n’y a qu’un type de pinceau en géométrie elliptique, il n’y a aussi qu’un type de cycle. La macro cercle support sert essentiellement pour animer des points sur le cercle elliptique.
Le dossier Technique
A priori, sauf exception, et à vouloir montrer, en présentation, comment fonctionne le modèle, ces macros ne sont pas utiles dans des constructions standards. Par contre elles ont servi à construire les précédentes, comme c’est largement détaillé dans les sections suivantes de cet article.
Pour une utilisation de ces macros, lancer cette figure dans un nouvel onglet.
Premiers exemples élémentaires d’utilisation
L’axiome de Pasch
Lancer la figure de base avec toutes les macros dans un nouvel onglet.
Il s’agit de montrer que si une droite coupe un côté du triangle, quand ce triangle est de type elliptique, elle peux ne couper aucun autre côté, ou couper les trois côtés.
On n’utilise que deux macros du dossier Droites : les macros Segment Elliptique et Droite 2 pts.
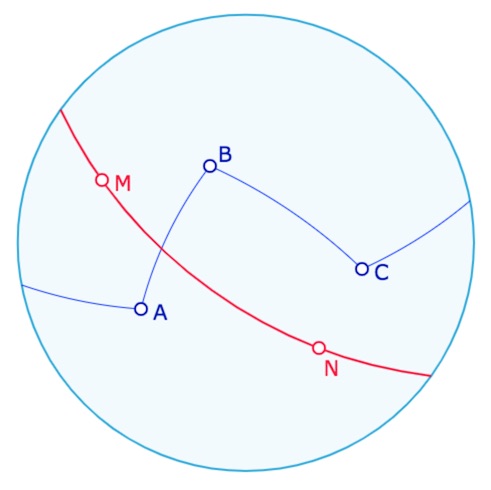
Préférer ouvrir cette figure dans un nouvel onglet
Les droites des milieux
(Proposition de construction longue en 3 étapes, avec chargement intermédiaire possible)
Lancer la figure de base avec toutes les macros dans un nouvel onglet.
Il s’agit juste d’illustrer simplement que les milieux sont alignés par trois. Cette figure utilise seulement deux macros : droites et milieux. Les noms ont été renommés avec la palette « inspecteur des objets » (icone « roue »). On pourrait ajouter par exemple la polaire de \(Jbc\) pour illustrer qu’elle passe par \(Ibc\).
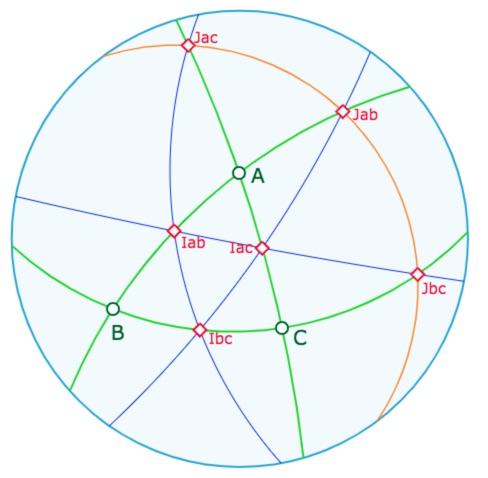
Préférer lancer cette figure dans un nouvel onglet pour prolonger la construction
Les cercles circonscrits
En effet, on poursuit cette figure, en ajoutant les pôles de des 4 droites des milieux : ce sont les 4 centres des cercles circonscrits à \(ABC\). Ci-dessous, là encore, les noms des pôles ont été renommés. Puis on rajoute les cercles. Avant cela, on a caché (icone « gomme ») les milieux et les droites des milieux.
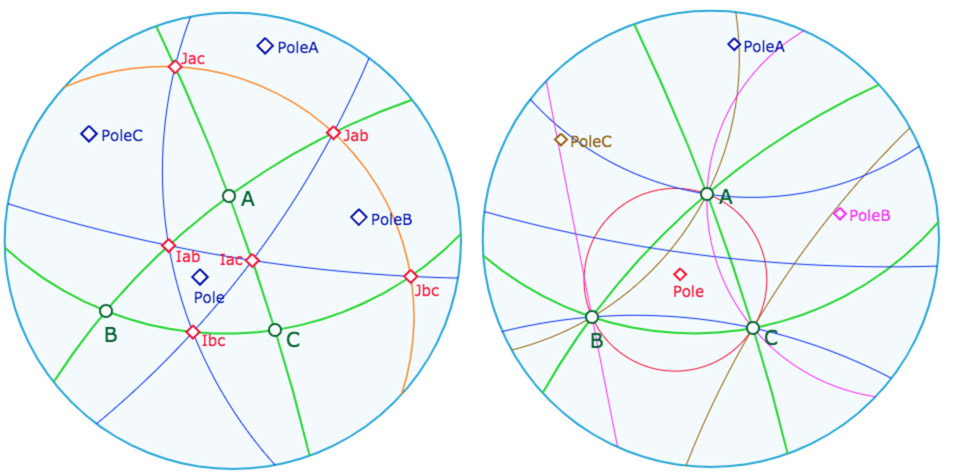
Préférer lancer cette figure pour manipuler et poursuivre la construction
Vérification des distances
(activité plus technique – nécessite d’utiliser un peu plus l’interface du logiciel)
On pourrait placer un point sur chacun des cercles et vérifier en le déplaçant que la distance au cercle est constante. On se propose pour une fois d’aller un peu plus loin. L’idée est de prendre deux points \(M\) et \(N\), d’aimanter le premier aux 4 centres, et le second aux 4 cercles – soit un cercle et 6 arcs de cercle. Cela se fait ainsi.
• Être en mode standard (flèche gauche activée). Créer deux points que l’on nommera \(M\) et \(N\).
• Pour le premier, choisir le comportement aimantation (dernière icone des comportements, à droite) puis montrer les 4 pôles un à un (laisser les 20 pixels d’aimantation). Ensuite re-selectionner la flèche du tableau de bord pour quitter le mode aimantation.
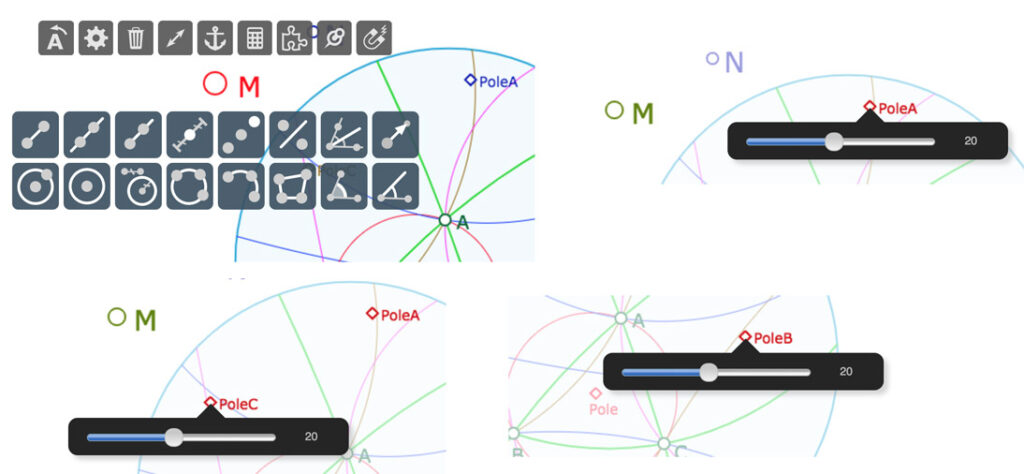
Ici on montre l’aimantation de trois des 4 pôles, mais aimanter aussi avec le quatrième.
• Puis aimanter le point \(N\) sur les 4 cercles circonscrits, soit le cercle de centre \(Pole\) et les 6 arcs de cercles qui représentent les 3 autres cercles circonscrits. On voit sur l’illustration suivante toutes les aimantations (en rouge) du point \(N\). Penser à retourner sur la flèche pour dé-selectionner le mode aimantation.
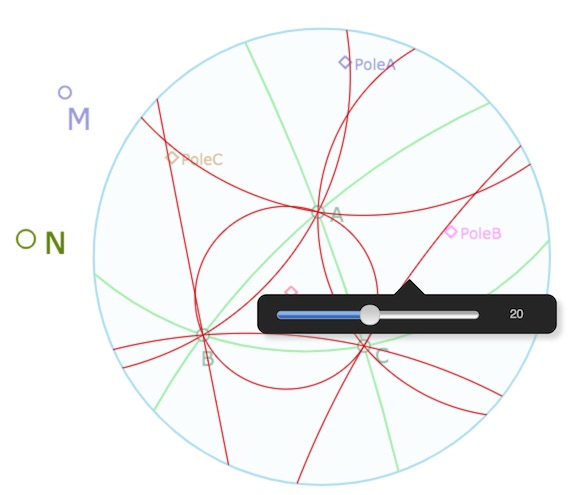
Les aimantations du point \(N\)
Placer ensuite \(M\) et \(N\) dans le disque et appliquer la macro distance à ces deux points. On peut ajouter des décimales dans l’inspecteur d’objets. On peut revenir ensuite en mode « consultation », la flèche gauche du tableau de bord désactivée, c’est plus simple. Placer \(M\) sur un centre de cercle – un des pôles – et \(N\) sur l’un des arcs du cercle associé. Déplacer \(N\), puis le placer sur l’autre arc représentant le même cercle.
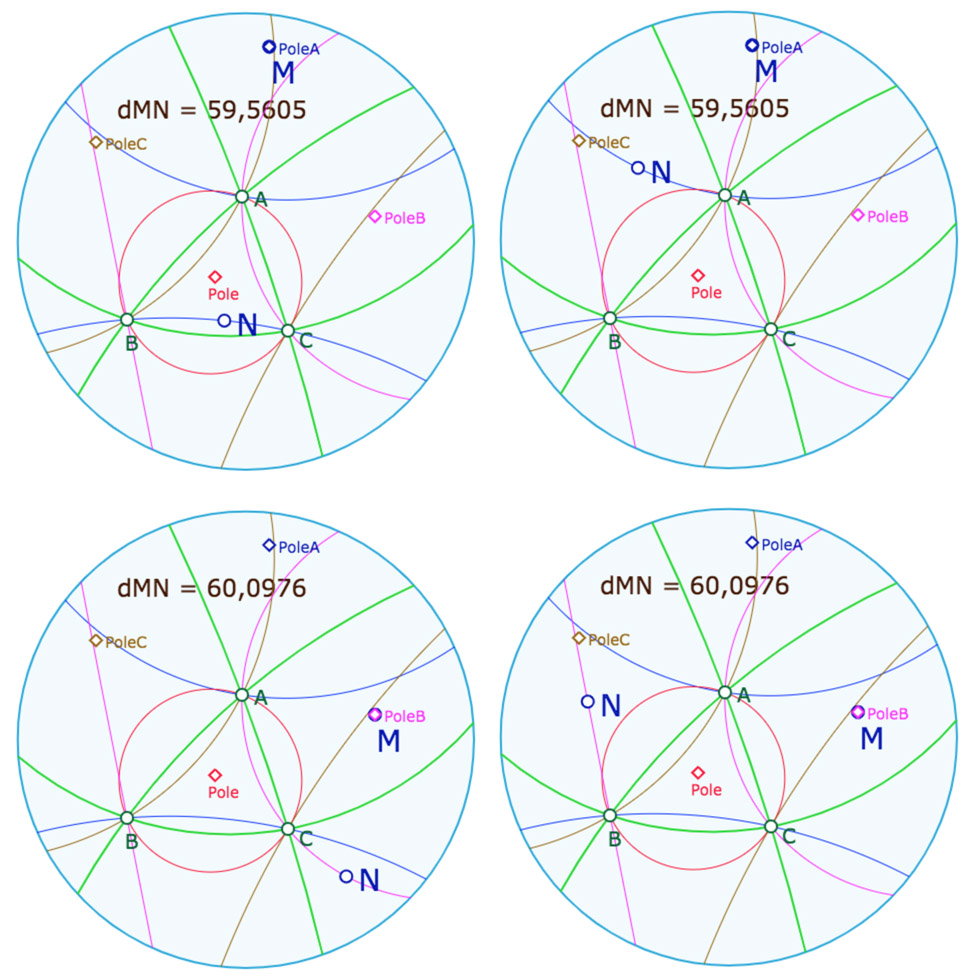
Deux des différentes illustrations possibles. En haut \(M\) en \(PoleA\), en bas en \(PoleB\).
Dans les deux cas \(N\) sur les deux arcs de cercles associés.
Préférer ouvrir cette figure finale dans un nouvel onglet
Construction de polygones réguliers
Dans cette section, on propose la construction tout d’abord d’un octogone régulier étoilé. Le principe préliminaire, pour une animation est détaillé, il sera ensuite applicable à toute situation. On prolongera par un polygone à 16 côtés.
Préparation d’un point animé sur un cercle elliptique
On se donne deux points, le centre \(O\) et un point pour la taille du cercle, nommé \(taille\). On construit alors le cercle euclidien support, en pointillé gris ci-dessous, et le cercle elliptique, rouge ci-dessous. On prend un point \(M\) sur le cercle support, et on construit \(A\) son point elliptique.

On peut alors construire un polygone régulier de centre \(O\) à partir du point \(A\), tel qu’une animation sur \(M\) permet de faire tourner le polygone … tout en pouvant modifier sa taille par le point du même nom.
Premier point du polygone
C’est dans cette partie que l’on propose des méthodes pour lesquelles il faut être attentif. On construit la droite elliptique \((OA)\) on fait apparaître son centre, caché, on le nomme ici \(coA\).
Remarque : techniquement, il y a deux points l’un sur l’autre. Le premier est le centre du cercle qui a servi à construire l’arc représentant la droite elliptique. Le centre de la droite elliptique est le second point.
Pour des questions d’orientation, on préfèrera construire le premier point comme symétrique par rapport à la bissectrice entre le point \(A\) et le premier point à construire (par principe, même si ce n’est pas indispensable pour un octogone). Donc pour construire un point à un angle \(\displaystyle \frac{2\pi}{n}\), on prend la moitié, on construit la droite à \(\displaystyle \frac{\pi}{n}\).

La figure en l’état de cette illustration peut être lancée ci-dessous
Pour un report d’angle en \(O\), il faut deux points. Toujours pour des raisons d’invariance de l’orientation de la perpendiculaire à \([O\, cOA]\) on choisit d’utiliser une rotation par les nombres complexes d’où le point \(pOrtho=O+i(cOA)O)/2\). De là on construit une demi-droite à l’angle 22,5° de la tangente à la droite elliptique en \(O\). Pour cela on met un angle quelconque, et on adapte, en mode « calculatrice » comme dans l’illustration ci-dessus.
Le centre de la droite elliptique cherchée (verte ci-dessus) est sur la perpendiculaire à la demi-droite construite par l’outil « report d’angle » et sur la médiatrice de \(O\) et \(antiO\). C’est le point \(cSym\). Le premier point de l’octogone est le symétrique de \(A\) par rapport à cette droite.
Préférer lancer la figure dans l’état de l’illustration précédente dans un nouvel onglet pour poursuivre la construction.
Finalisation de l’octogone
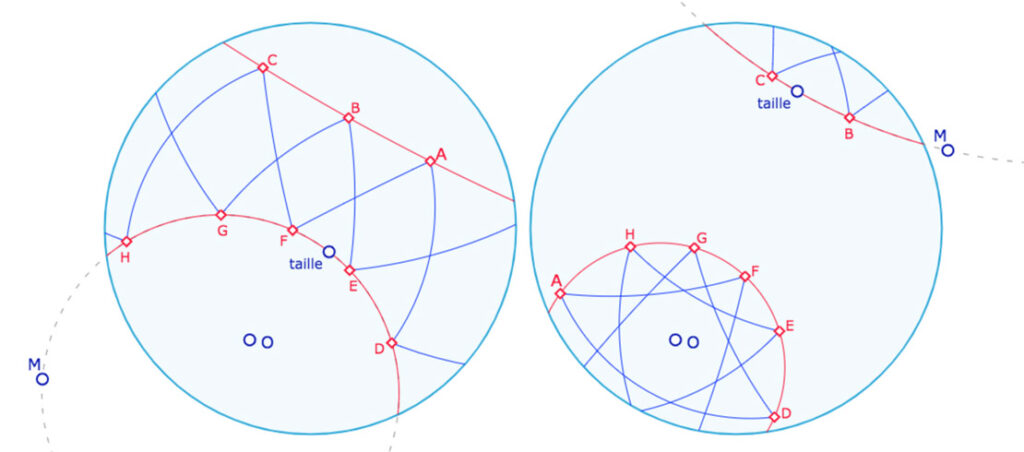
Le point \(B\) est le symétrique de \(A\) rapport à la bissectrice » verte. On construit ensuite \((OB)\) ce qui permet de construire \(C\) et ainsi de suite … Le point \(D\) est sur \((OA)\) car c’est le symétrique de \(A\) par rapport à \(O\). Donc on termine les sommets de l’octogone sans construire de nouvelles droites.
Remarque : en pratique il est bien moins « onéreux » en terme d’objets de construire les droites et le symétrique par rapport à une droite plutôt que des symétries centrales qui construisent par défaut les polaires des points.
Le polygone étoilé P(8,3)
On construit alors les segments en sautant deux points. Éventuellement, se placer dans le cas où le cercle elliptique est représenté par un cercle euclidien (et pas deux arcs de cercle).
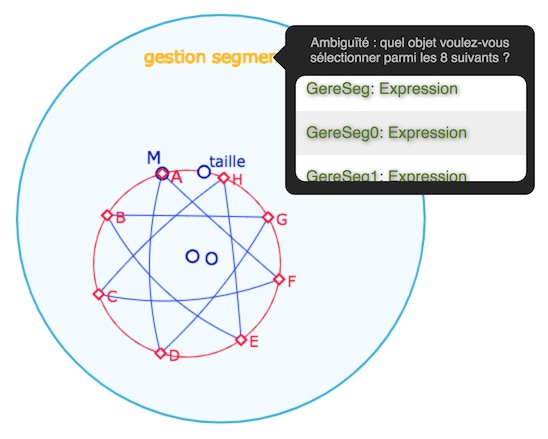
Pour des raisons esthétiques, on cachera la gestion des segments : il y a 8 expressions l’une sur l’autre, même si ce n’est pas indispensable non plus.
Finalisation
On lance une animation sur \(M\), avec l’icone « ressort », la dernière icone à droite de la palette de comportement.
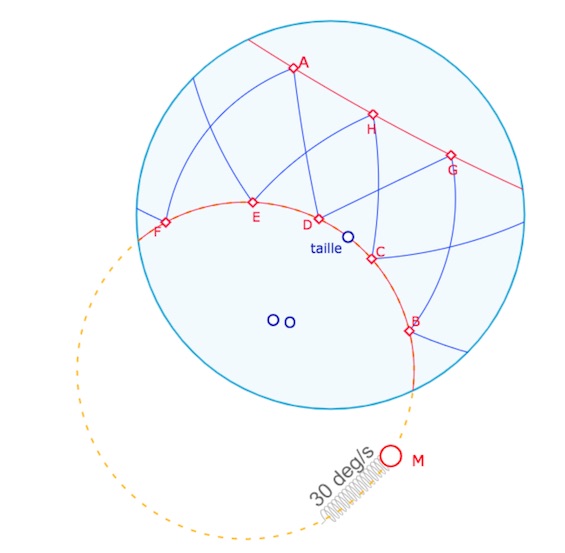
En arrêtant l’animation quand \(M\) est en dehors du disque elliptique, on peut cacher à la fois le cercle support, et même le point \(M\) lui-même, puis relancer l’animation.
Préférer lancer la figure finalisée dans un nouvel onglet.
Variante sur un polygone à 16 côtés (hexadécagone)
On modifie simplement l’angle de la première bissectrice
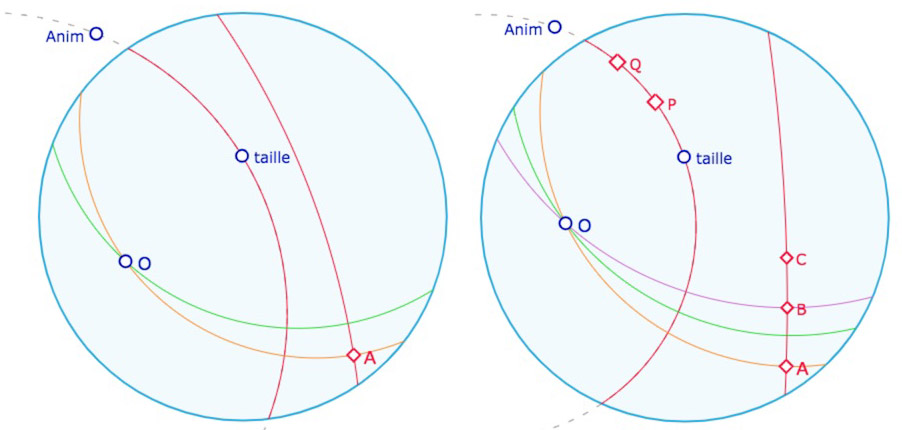
Lancer la figure précédente (état de gauche ou état de droite) dans un nouvel onglet pour poursuivre la construction des points, ou encore l’hexadécagone avec tous ses sommets comme ci-dessous.
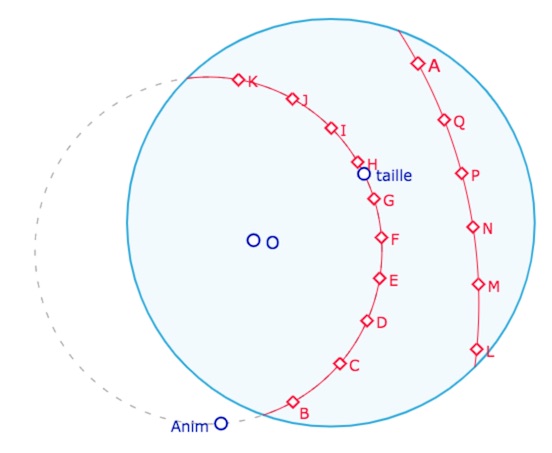
Une fois les 16 points du polygone construit, on peut choisir un des trois types du polygone étoilé, soit P(16,3), P(16,5) ou P(16,7), les autres choix produisant les mêmes polygones. Voici 5 illustrations de P(16,5). On cachera les 16 expressions « gestion segment », puis le cercle support euclidien et le point \(Anim\) avant de relancer son animation, comme dans le cas de l’octogone.
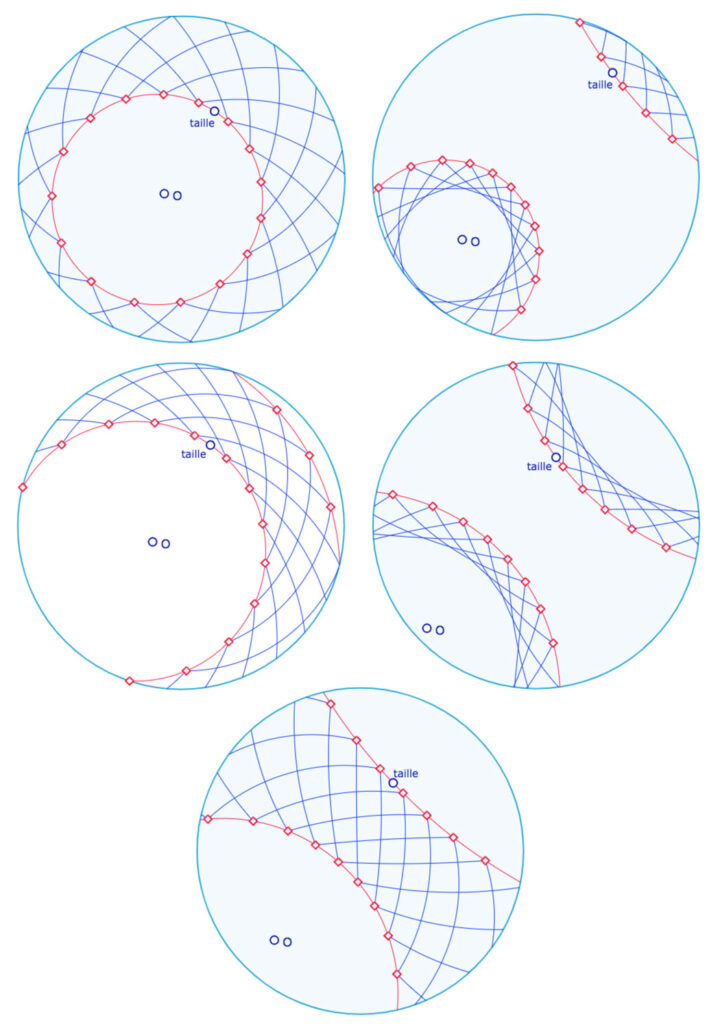
Préférer lancer cette figure (un peu longue à ouvrir) dans un nouvel onglet.
Variante hexadécagone étoilé P(16,7)
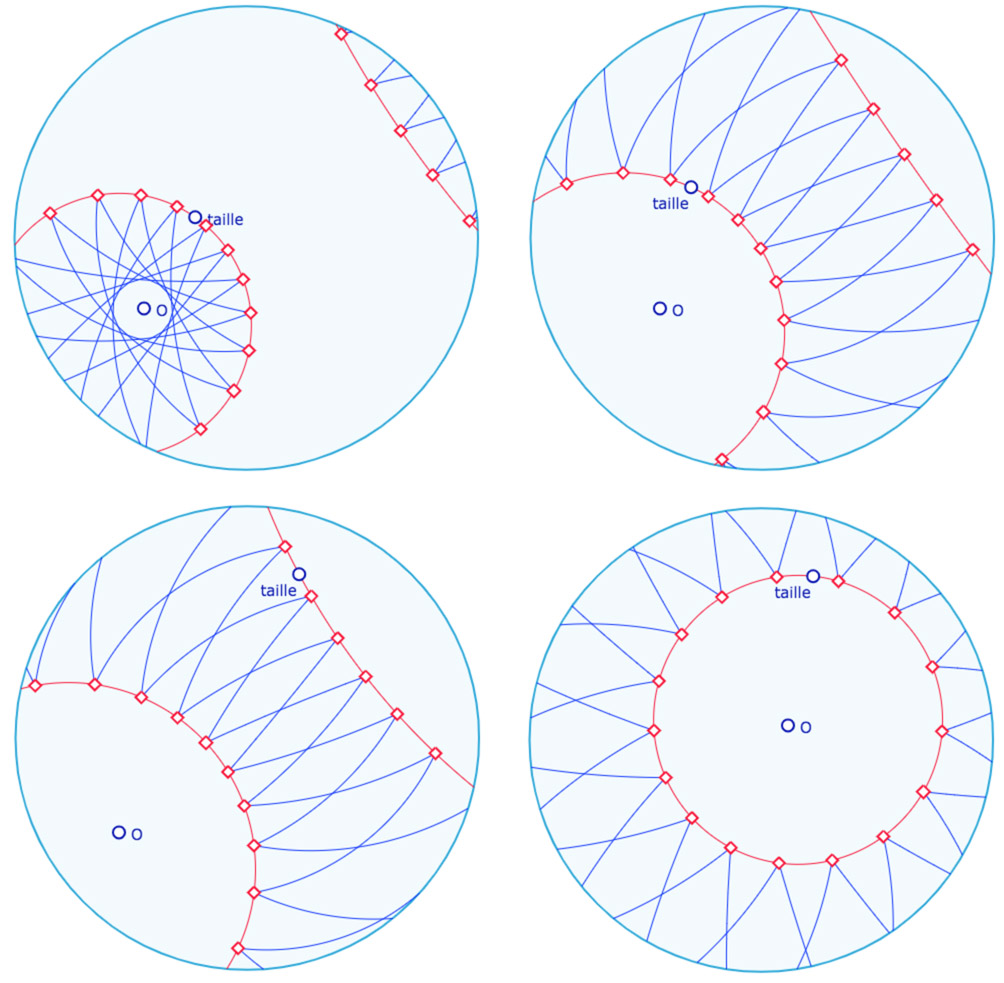
Préférer lancer cette figure finie dans un nouvel onglet.
Réalisation des premières macros
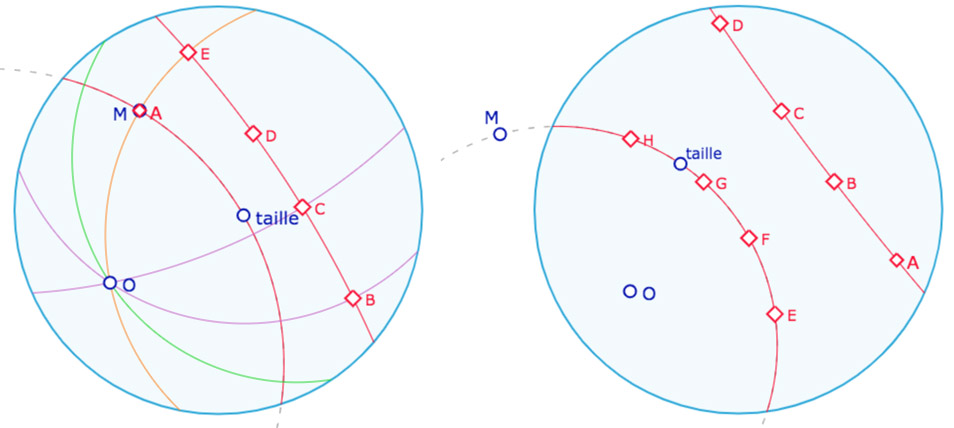
Rappel de l’obtention du modèle plan depuis la sphère
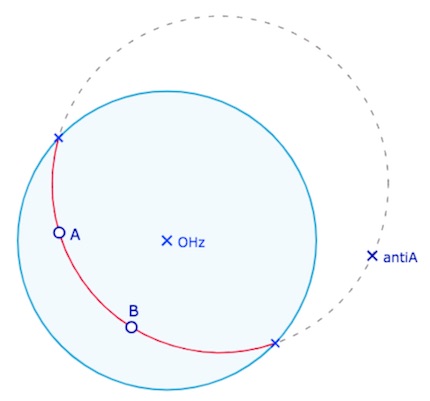
Le modèle utilisé est donc le modèle plan de Klein, projection stéréographique de la sphère de Riemann, où les points opposés sont identifiés. Pour rendre compte du modèle plan, on part de la sphère. Les points opposés sont identifiés, et on projette la sphère stéréographiquement depuis le pôle Nord sur le plan tangent au pôle Sud.
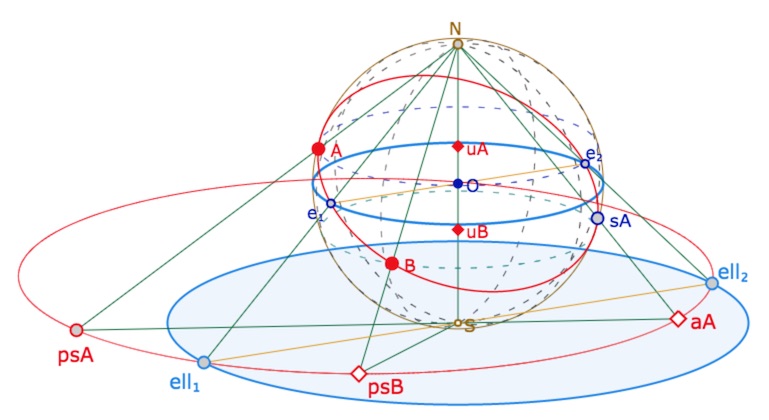
Les points \(A\) et \(B\) de la sphère sont projetés en \(psA\) et \(psB\) (\(ps\) pour « projection stéréographique ») Mais comme \(A\) est dans l’hémisphère Nord, on projette aussi son symétrique \(sA\) par rapport au centre de la sphère, ce qui donne le point \(aA\) à l’intérieur du cercle, \(a\) pour antipodie – ici antipodie spatiale composée commutative de la symétrie centrale de centre \(O\) et de la \(ps\). Dans le plan, \(aA\) est l’antipodie plane de \(psA\) c’est-à-dire la composée – toujours commutative – de la symétrie de centre le centre du cercle et de l’inversion du même cercle. Le point elliptique correspondant au point \(A\) de la sphère est celui des deux (entre \(psA\) et \(aA\)) qui est à l’intérieur du disque de Klein, lui-même projeté de l’équateur.
On rappelle que les points opposés du cercle \(Hz\) sont identifiés : pour la géométrie elliptique les points \(ell_1\) et \(ell_2\) sont un seul et même point car c’est le cas des points de l’équateur \(e_1\) et \(e_2\) sur la sphère.
La droite elliptique passant par les points \(psB\) et \(aA\) (deux points du disque) est l’arc de cercle passant par ces deux points et coupant le cercle \(Hz\) en les points opposés \(ell_1\) et \(ell_2\) .
Dans toute la suite – comme pour le cas hyperbolique – le disque du modèle elliptique est centré sur l’origine du repère, ainsi le symétrique d’un point \(A\) est le point \(-A\). Dans les macro constructions, le premier objet à montrer est ce cercle de Klein.
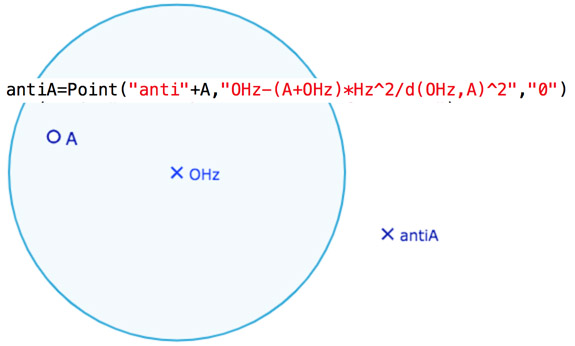
L’antipodie plane
Elle se traite en une seule ligne en incorporant l’opposé d’un point dans la formule
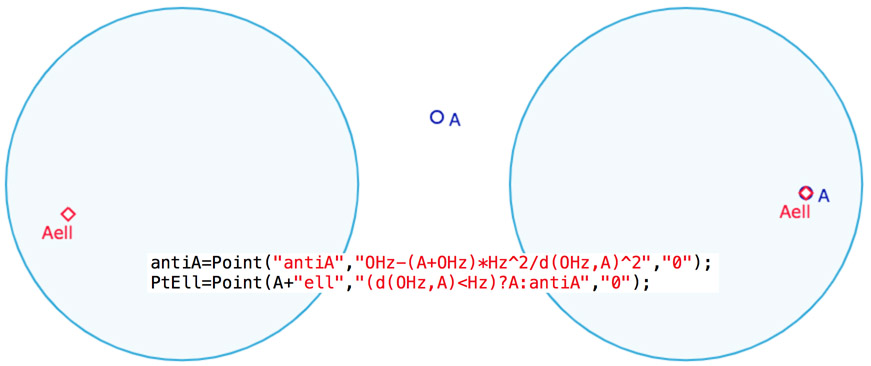
Le point elliptique
Le point elliptique est donc celui des deux points entre \(A\) et \(antiA\) qui est à l’intérieur du cercle
Le symétrique d’un point par rapport à une droite est le point elliptique associé à l’inverse du point par rapport à la droite.
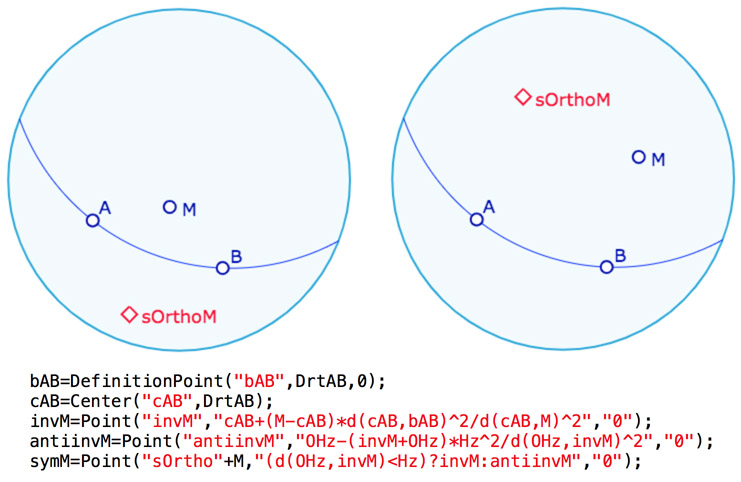
Cette illustration est essentiellement proposée pour montrer le traitement effectué selon que l’inverse est pris selon un cercle (avec le cercle \(Hz\) en particulier) ou selon un arc de cercle. En effet, si le nom d’un cercle est une variable qui représente son rayon, ce n’est pas le cas d’un arc de cercle. On prend donc un point « du bord de la droite », le point \(bAB\) – qui est un point de définition de l’arc donc ne crée pas de point supplémentaire – et on utilise la distance \(d(cAB, bAB)\) à la place du rayon. C’est aussi la raison pour laquelle on dispose de deux macros d’inversion, même si on pourrait les unifier mais au pris d’ajouter quelques objets dans des situations où ce n’est pas nécessaire.
Construction d’une droite elliptique
La droite passant par \(A\) et \(B\) est l’arc de cercle passant par les points \(A, B\) et \(antiA\). Comme on dispose d’un outil de construction « Cercle par 3 points », la construction se fait donc avec très peu d’objets
Contrairement à ce qui a été fait pour les macros hyperboliques du disque de Poincaré, ici, le premier des deux points sélectionnés est un objet de définition de l’arc représentant la droite, ce qui servira pour la construction du pôle d’une droite.
Construction du pôle d’une droite
Pour des raisons de symétrie, le pôle d’une droite est sur la droite des centres – du cercle du modèle et du cercle représentant la droite. Toute droite ayant un point constituant à l’intérieur du cercle (ci-dessous \(A\)), on prend la perpendiculaire à la droite en ce point – c’est-à-dire le cercle orthogonal. Son centre est l’intersection de la médiatrice de \(A\) et \(antiA\), et de la perpendiculaire à \(c_{AB}A\) en \(A\). Ce cercle coupe la demi-droite \([O_{Hz} \, c_{AB})\) en le pôle de la droite.

La perpendiculaire à une droite passant par un point \(M\) – autre que le pôle de la droite – est la droite passant par \(M\) et le pôle de la droite.
Les médiateurs et les milieux
La médiatrice de \(A\) et \(B\) est un axe de symétrie. On peut construire facilement d’abord celui qui passe « entre » les deux points, au sens euclidien, et ensuite le second. Tout d’abord si la symétrie – sous forme d’inversion – échange \(A\) et \(B\) le centre du cercle associé est sur la droite \((AB)\). Le cercle passe aussi par le pôle de \((AB)\) puisque la médiatrice est orthogonale à la droite, et donc son centre est sur la médiatrice du pôle de et son antipodie.
On a donc le centre par intersection de deux droites (ci-dessous orange et rouge bordeaux).
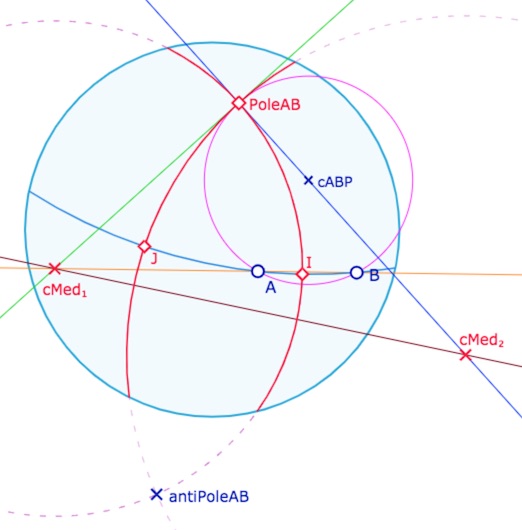
Le cercle de l’illustration, circonscrit à \(A, B\) et \(Pole_{AB}\) ne sert pas dans cette construction. Il a été ajouté pour décrire un autre argument. En notant provisoirement \(K\) le centre du cercle d’inversion cherché, comme on doit avoir aussi \(KA.KB = KP^2\) par définition de l’inversion, ce point \(K\) – propriété de la puissance d’un point – est aussi sur la perpendiculaire à \(c_{ABC}Pole_{AB}\) en le pôle. Cette droite (verte ci-dessus) passe aussi par le centre cherché mais n’est pas utilisé dans la constrution finale.c
On construit ainsi, en très peu d’objets, les deux centres des médiatrices. Pour le second, on n’a pas besoin du centre \(c_{ABC}\), on utilise simplement la perpendiculaire à \(cMed_1 \, Pole_{AB}\) en le pôle. Les points \(I\) et \(J\), intersection des deux médiatrices et de la droite \((AB)\) sont les milieux des deux points \(A\) et \(B\).
Les macros angles – longueurs – distances – segments
Les angles étant conformes (par la projection stéréographique) la construction est élémentaire

L’angle en \(A\) est le supplémentaire de l’angle formé par les centres des droites elliptiques \(c_{AC}Ac_{AB}\) et si on veut l’afficher sur la figure, il faut prendre les perpendiculaires aux rayons et prendre l’angle \(h_{AC}Ah_{AB}\).
Pour le fun … les marques d’un triangle tripolaire …
Dans les pages du menu ELL, l’angle avait été construit en prévision de la longueur puisque la longueur entre deux points \(A\) et \(B\) est l’angle \(\angle APB\) où \(P\) est le pôle de \((AB)\).
Longueur avec les nombres complexes
La longueur d’une droite est égale à \(\pi\), pour un cercle de rayon 1. On garde la même longueur pour un cercle quelconque, puisque c’est fondamentalement proportionnel à un angle. Comme on a utilisé les nombres complexes dans certaines macros hyperboliques, on se propose de faire de même ici. En effet la longueur elliptique entre deux points d’affixe \(z_1, z_2\) dans le cercle unité est donnée par \(long(A,B) = \displaystyle 2 atan \left \vert \frac{z_1-z_2}{1+\bar{z_1}z_2} \right \vert\), ce qui devient, pour un cercle de rayon \(Hz\) :
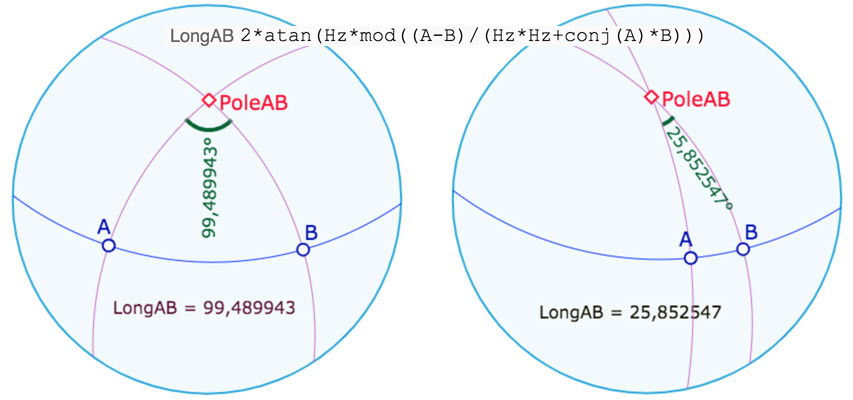
Comparaison des deux méthodes de calcul de la longueur
La distance est alors \(d(A,B) = min(180-long(A,B), long(A,B))\).
Segments
Le segment elliptique est celle des deux parties de la droite de longueur inférieure à 90°, soit la partie euclidienne entre \(A\) et \(B\), soit l’extérieur, c’est-à-dire les deux arcs \(bdA \, A\) et \(bdB \, B\). On construit alors trois autres points, les milieux euclidiens des arcs, pour construire ces trois arcs. Sur l’illustration on a fait figuré le calcul du milieu \(mbdAA\), et la gestion globale du segment elliptique.

Polaire d’un point
Là encore, on trouve rapidement une construction élémentaire, avec peu d’objets intermédiaires. Voici une construction très synthétique. Soit \(P\) un point. Le centre euclidien de la polaire de \(P\) est sur la droite passant par \(P\) et son antipodique \(antiP\). On note \(pC\) le milieu de \(P\) et \(antiP\). Alors l’antipodique de ce point (\(antipC\) si dessous) est le centre euclidien cherché. En fait, le cercle de centre \(pC\) passant par \(P\) donne les points « équateur » de la polaire … ce qui inspire pour le centre euclidien de la polaire …
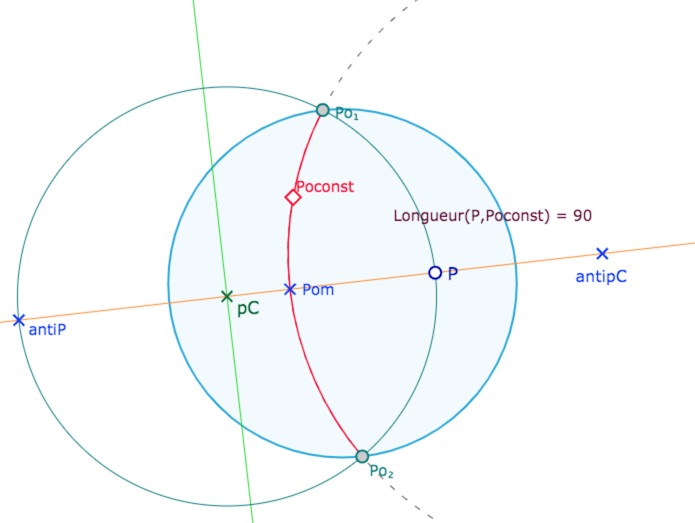
Note technique : on aurait pu construire la polaire à partir des points \(Po_1, Po_m\) et \(Po_2\). Mais \(Po_m\) étant au milieu de l’arc, certaines macros (dont celle du Pôle) utilisant ce « point définition » ne fonctionnent plus, deux droites dont on utilise l’intersection devenant parallèles. D’où l’ajout d’un autre point, \(Po_{const}\), là encore milieu euclidien sur l’arc des deux points \(Po_m\) et \(Po_1\).
Les macros bissecteurs – Points bissecteurs – Cercle
Comme en géométrie elliptique, on dispose de la polarité, on peut reprendre l’argument déjà détaillé dans cette page d’introduction au point de vue de Daniel Perrin, et en particulier cette conclusion :
La question de l’existence des bissectrices de deux droites est équivalente à celles des médiatrices et milieux de leurs pôles.
Daniel Perrin – DPPartie4 – p99 (voir le lien ci-dessus)
Étant données deux droites \((AB)\) et \((AC)\), les bissectrices et les points bissecteurs de ces deux droites sont les médiatrices et les milieux de leurs pôles. Compte tenu des macros précédentes, la construction est immédiate. Ci-dessous, en rouge les deux bissectrices des droites et leurs points bissecteurs \(bissA_1\)\(bissA_2\) qui sont à la fois les centres de symétrie des deux droites et les milieux de leurs pôles.
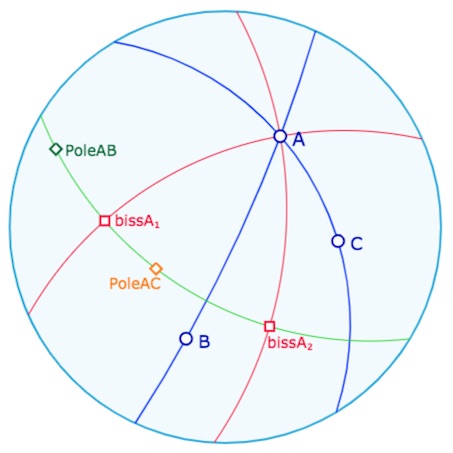
Comme milieu des pôles des droites, les deux points bissecteurs sont sur la polaire de \(A\), ce qui, géométriquement est une évidence, car envoyant un point d’une droite sur l’autre droite la symétrie centrale par rapport à un point bissecteur ne peut envoyer \(A\) que sur lui-même.
Autre argument : un point bissecteur étant le pôle de la bissectrice qui ne le contient pas, il se comporte comme la symétrie orthogonale par rapport à cette bissectrice, et donc laisse \(A\) invariant.
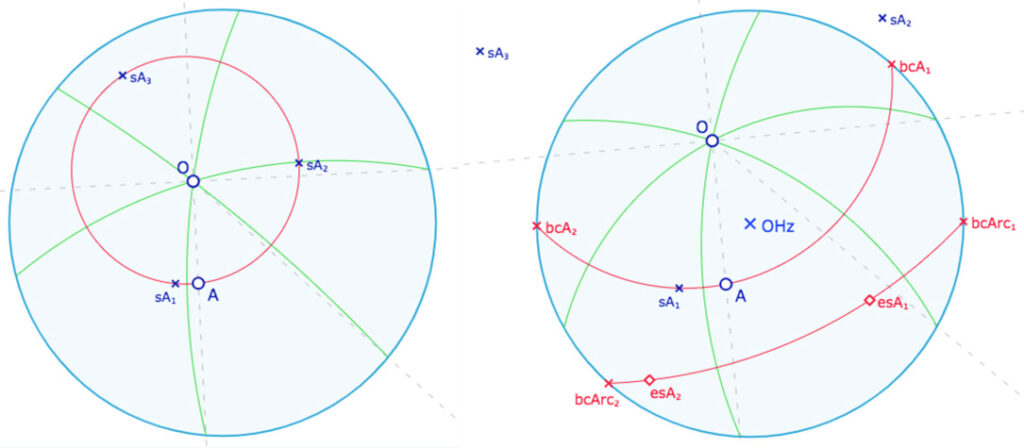
Le cercle \(\mathbf{C(O, A)}\)
On construit trois points du cercle à partir des points de référence \(O\) et \(A\), pour que cela passe aux macros. à gauche le cercle elliptique est un cercle euclidien – que l’on appellera dans les macros le « cercle support ». dans l’illustration de droite, deux points sortes du cercle modèle, les points \(esA_1\) et \(esA_2\) sont obtenus par la macro « Point elliptique ».