« […] deux figures sont égales quand on peut les superposer ; pour les superposer il faut déplacer l’une d’elles jusqu’à ce qu’elle coïncide avec l’autre, mais comment faut-il la déplacer ? Si nous le demandions, on nous répondrait sans doute qu’on doit le faire sans la déformer à la façon d’un solide invariable. Le cercle vicieux serait alors évident.[…] Cependant toute imparfaite qu’elle soit, cette définition implique un axiome. La possibilité du mouvement d’une figure invariable n’est pas une vérité évidente par elle-même, ou du moins elle ne l’est qu’à la façon du postulatum d’Euclide et non comme le serait un jugement analytique a priori. D’ailleurs en étudiant les définitions et les démonstrations de la géométrie, on voit qu’on est obligé d’admettre, sans les démontrer, non seulement la possibilité de ce mouvement, mais encore quelques-unes de ses propriétés. »
Poincaré, La Science et l’hypothèse (1902)
Historiquement, l’utilisation du mouvement dans les démonstrations de géométrie a toujours posé problème : depuis Euclide, qui n’y recourt qu’une seule fois au tout début de ses Éléments, en passant par Proclus qui le dénonce, puis les différentes écoles arabes du IXe au XIIe siècle, certains mathématiciens l’utilisant (al-Haytam), d’autres le refusant (al-Kayyam), jusqu’à Wallis qui l’utilise encore explicitement, le mouvement en géométrie traduit bien l’ambiguïté de la relation entre le monde sensible, sa modélisation, puis – pour les mathématiques – son axiomatisation. C’est essentiellement un rapport à la réification des objets mathématiques.
La démarche de David Hilbert, dans ses «Fondements de la géométrie», rentre dans cette problématique du rapport au mouvement, puisque, comme le souligne Poincaré, il axiomatise les propriétés attendues du mouvement en introduisant des axiomes minimaux de congruence de segments et d’angles. Au cours des différentes éditions, de la première en 1899 à la dernière de son vivant (la septième, en partie réécrite) en 1930, Hilbert a affiné sa réflexion, et par exemple, transformé des axiomes en théorèmes.
Les axiomes de Hilbert
L’objectif de David Hilbert est une construction catégorique – tous les modèles sont isomorphes – du plan euclidien (et de l’espace), avec un minimum d’axiomes, donc nécessairement forts pour arriver rapidement au corps de nombres qui soit l’ensemble des nombres réels. Ce sont les axiomes de continuité.
En dehors de la première édition dans laquelle il pensait que ses axiomes étaient indépendants les uns des autres, Hilbert a rapidement organisé ses axiomes en cinq groupes indépendants d’axiomes :
• Les axiomes d’appartenance (I, 1 à 8)
• Les axiomes d’ordre (II, 1 à 4)
• Les axiomes de congruence (III, 1 à 5)
• L’axiome des parallèles (IV)
• Les axiomes de continuité (V, 1 et 2)
Les axiomes du groupe I – les axiomes d’appartenance
Sur les huit axiomes, les trois premiers sont les axiomes du plan – les axiomes usuelles d’incidence – les cinq derniers sont des axiomes spatiaux.
I.1. et I.2. (existence et unicité) Deux points distincts sont sur une et une seule droite.
I.3. Sur une droite il y a au moins deux points. Il existe au moins trois points non alignés.
Les cinq autres axiomes, spatiaux, peuvent se résumer en ces trois axiomes
I.4. et I.5. (existence et unicité). Trois points non alignés sont sur un et un seul plan.
I.6. Si deux points d’une droite sont sur un plan, tous les points de la droite sont sur ce plan.
I.7. et I.8. Il existe au moins trois points non coplanaires. Si deux plans ont un point commun, ils en ont au moins un autre.
Les axiomes du groupe II – les axiomes d’ordre
II.1. Si un point \(B\) est entre un point \(A\) et un point \(C\) les trois points \(A, B, C\) sont sur une droite et \(B\) est aussi entre \(C\) et \(A\).
II.2. Etant donnés deux points \(A\) et \(C\), il existe au moins un point \(B\) sur la droite \((AC)\) qui soit entre \(A\) et \(C\) .
II.3. De trois points d’une droite, il n’y a pas plus d’un qui soit entre les deux autres.
II.4. (Axiome de Pach) Si une droite du plan d’un triangle ne passe par aucun sommet et rencontre un des côtés, alors elle rencontre un des deux autres côtés.
On notera qu’il n’y a pas d’axiomes spatiaux d’ordre, seulement trois axiomes linéaire et un axiome plan. Å partir des deux premiers groupes d’axiomes, on montre rapidement qu’une droite contient une infinité de points. Cela exclu donc les géométries finies (à cause de II.3). Ce même axiome, ou encore le seul II.4, évacue aussi la géométrie elliptique.
Segment AB : Soient deux points \(A\) et \(B\). Les points de la droite \((AB)\) situés entre \(A\) et \(B\) forment le segment \(AB\) (ou \(BA\) ). Les points entre \(A\) et \(B\) ont les points intérieurs au segment, \(A\) et \(B\) sont les extrémités du segment. Tous les autres points de la droite sont extérieurs au segment\(AB\) .
Les axiomes du groupe III – les axiomes de congruence
Premier groupe, sur les segments : les axiomes linéaires du groupe III
Définition : entre les segments, il existe certaines relations, exprimées par les mots congruent ou égal.
III.1. Sur une droite donnée et d’un côté d’un point \(A\) donné, il existe un point \(B\) tel que le segment \(AB\) soit congruent à un segment donné.
III.2. Si deux segments sont congruents à un même troisième ils sont congruents entre eux.
III.3. Si \(B\) est entre \(A\) et\(C\) , si \(B’\) est entre \(A’\) et \(C’\), si \(AB\) et \(A’B’\) sont congruents, et si \(BC\) et \(B’C’\) sont congruents, alors \(AC\) et \(A’C’\) sont congruents.
Le premier axiome introduit la notion de report de segment (l’unicité de \(B\) est alors montrée). Le deuxième aboutit à ce que la congruence des segments soit une relation d’équivalence (la réflexivité n’est pas immédiate, c’est une conséquence de III.2). Le troisième axiome donne la possibilité d’additionner des segments.
Second groupe, sur les angles : les axiomes plans du groupe III
Soient deux demi-droite \(h\) et \(k\) différentes de même origine \(O\), et appartenant à des droites différentes, l’ensemble de ces deux demi-droites est appelé un angle. On parle de l’angle \(\angle(h,k)\) ou \(\angle(k,h)\) – les deux symboles désignent le même objet. La définition exclu l’angle plat, l’angle nul mais aussi les angles concaves. \(O\) est appelé sommet de l’angle, les demi-droites sont les côtés de l’angle. Au moyens des axiomes des deux premiers groupes, on montre les premières propriétés usuelles comme l’intérieur d’un angle.
Si un angle est de sommet \(B\) et dont les côtés contiennent respectivement les points \(A\) et \(C\), on parle de l’angle \(\angle BAC\).
Puis on introduit la congruence des angles, comme pour les segments. Le report d’angle se traite comme celui de segment, mais l’unicité doit être demandée axiomatiquement alors qu’elle est démontrée pour les segments, justement par les angles, comme première conséquence des deux axiomes suivants.
III.4. Dans un plan donné, et d’un côté d’une demi droite \(h\) donnée, il existe une unique demi-droite \(k\) telle que l’angle \(\angle(h,k)\) soit congruent à un angle donné.
III.5. Si dans deux triangles \(ABC\) et \(A’B’C’\) on a les congruences entre les segments \(AB\) et \(A’B’\) , entre les segments \(AC\) et \(A’C’\) ainsi que la congruence entre les angles \(\angle BAC\) et \(\angle B’A’C’\) alors on a aussi la congruence entre les angles \(\angle ABC\) et \(\angle A’B’C’\).
L’axiome III.5 est la pierre angulaire de ce menu, puisque c’est sa mise en défaut qui permet l’émergence des géométries non arguésiennes. C’est aussi l’axiome qui fait le lien entre la congruence des segments et celle des angles.
Plan de Hilbert : traditionnellement, on appelle plan de Hilbert un plan qui vérifie ces trois premiers groupes d’axiomes, plus précisément les trois axiomes d’incidence (les axiomes spatiaux d’appartenance ne sont pas utiles puisque l’on est dans un plan), les axiomes d’ordre, et les axiomes de congruence.
Beaucoup d’études ont été produites sur les plans de Hilbert en étudiant les variantes sur la continuité ou les géométries non continues de plans de Hilbert. Nous y consacreront quelques pages de blog. Hilbert lui-même (1904) a reconstruit la géométrie hyperbolique, avec ces trois premiers groupes d’axiome, sans hypothèse de continuité. En particulier son fameux corps de extrémités est illustré de figures dynamiques ici.
Hilbert reprend ensuite l’exposé d’Euclide. Il définit alors l’angle supplémentaire d’un angle, puis l’ange droit comme étant égal à son supplémentaire. Il montre l’existence des angles droits, et leurs congruences, puis les trois cas d’égalité des triangles.
Les derniers théorèmes avant l’axiome des parallèles portent sur la possibilité de bissecter un angle et un segment.
L’axiome des parallèles (groupe IV)
Définition : deux droites coplanaires qui ne se coupent pas sont dites parallèles.
IV.1. Par un point \(A\) extérieur à une droite \(d\), dans un plan déterminé par \(A\) et \(d\), il passe au plus une parallèle à \(d\).
L’axiome proposé est minimaliste au sens où, avec les axiomes précédents, il en résulte aussitôt l’existence de cette parallèle. On en déduit aussi immédiatement que «Les angles d’un triangle font, ensemble, deux droits».
Les axiomes du groupe V – la continuité
Pour retrouver rapidement la géométrie euclidienne usuelle, et donc l’ensemble des réels comme corps de nombres construit à partir des configurations et de leurs propriétés géométriques, Hilbert utilise le fait que \(\mathbb{R}\) est le seul corps archimédien complet. On va retrouver ces propriétés avec deux axiomes, un d’archimédie et un de complétude.
V.1. (Archimédie) Si \(AB\) et \(CD\) sont deux segments quelconques, il existe un nombre entier \(n\) tel que le report du segment \(CD\) répété \(n\) fois à partir de \(A\) sur la demi-droite définie par \(B\) conduise à un point situé au delà de \(B\).
C’est l’axiome d’Archimède classique.
V.2. (Intégrité linéaire) L’ensemble des points d’une droite n’est susceptible d’aucune extension dans laquelle soient encore valable les axiomes d’ordre linéaires (II.1 à 3), de congruence linéaire (III.1 à 3) et l’archimédie (V.1).
Précision : en fait, dans cet axiome, Hilbert demande précisément «les propriétés fondamentales issues des axiomes des groupes II et III» et pas seulement la congruence linéaire car il faut avoir aussi l’unicité du report de segment qui nécessite les axiomes plans du groupe III. Ces subtilités, largement étudiées à travers les différentes éditions, ont été mise à jour, pour la 7° édition, par Bachmann dont nous avons (depuis la rédaction de cette page) présenté sa propre axiomatique dans le dernier menu de ce site.
Cet axiome V.2 permet d’arriver directement à \(\mathbb{R}\) (avec l’archimédie) car il permet de retrouver les coupures de Dedekind via le théorème de Bolzano (points d’accumulation). Plusieurs variantes des axiomes du groupe V ont été étudiées, équivalentes de cette version de la 7° édition.
La propriété de Desargues
Dans ses analyses de la causalité des propositions, Hilbert montre donc que, dans le cadre de la seule géométrie plane, la propriété de Desargues est une conséquence de l’axiome III.5, Puis il a montré que, sans cet axiome, on peut construire une géométrie vérifiant tous les autres axiomes (de Hilbert) mais pas cette propriété.
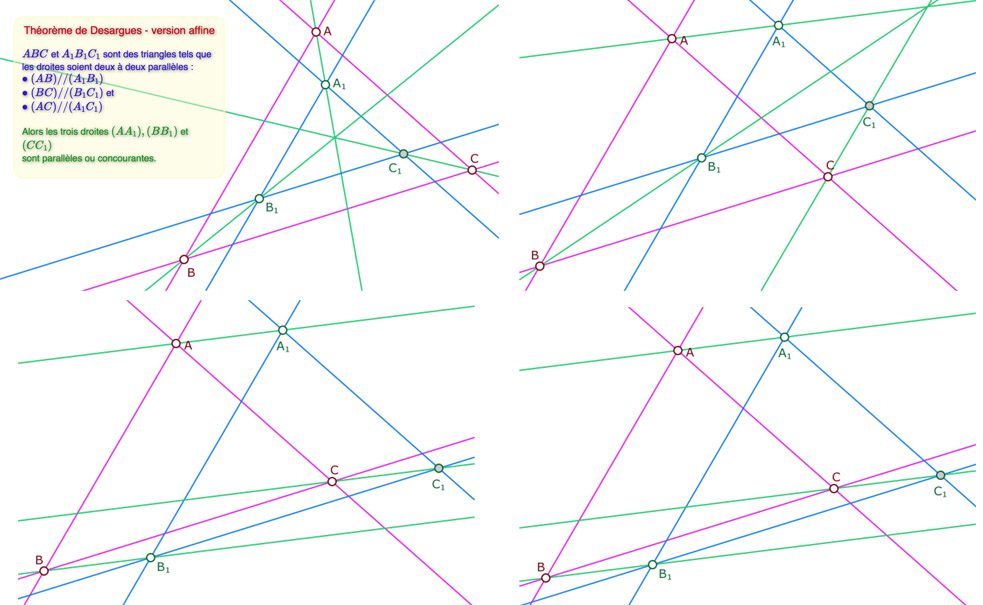
Par contre, le théorème de Desargues découle de l’existence de l’espace affine, par propriété de l’intersection des plans affines.
Il s’agit d’une figure 3D que l’on tourne au doigt ou à la souris. On déplace la figure par le point \(O\).
Les points \(A, B\) et \(C\) sont dans le plan du sol. Le point \(I\) est sur la verticale issue de \(pI\).
On peut agir sur tous les points autres que \(M, N, P\) qui sont construits. Le point \(C_1\)est aimanté sur \((IC)\) pour que \((B_1C_1)\) soit par parallèle à \((BC)\) et\(N\) à l’infini.
Hilbert montre ensuite que :
• sans le théorème de Desargues il n’est pas possible de construire de coordonnées. La multiplication n’est pas associative.
• avec le théorème de Desargues et sans l’axiome III.5 il est possible de construire une géométrie des coordonnées.
• avec le théorème de Desargues une géométrie affine plane peut toujours être considérée comme une partie d’une géométrie de l’espace vérifiant les axiomes affines.
Théorème d’Hessenberg : de Pappus à Desargues
Dans son étude approfondie des « Fondements de la géométrie » de Hilbert, Gerhard Hessenberg a montré que la configuration de Pappus (que Hilbert appelle «de Pascal») implique celle de Desargues. Sa démonstration est proposée dans la figure ci-dessous en quatre étapes. Elle peut être réservée à une seconde lecture.
«Etape – 1» pour présenter la figure, puis il y a quatre étapes. A chaque étape, on peut déplacer tous les points non construits.