Retour à la page de définition générale des droites du modèle de Hilbert
Droites (AB) avec A et B extérieurs à l’ellipse
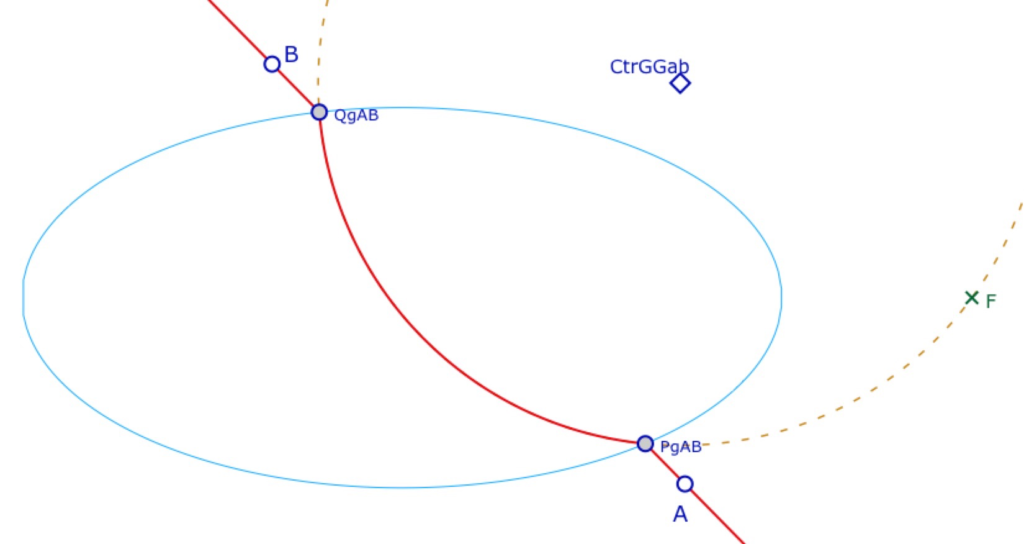
Ce premier cas ne pose pas de problème géométrique puisque l’on sait que le cercle circonscrit à \(F\) et aux intersections \(P\) et \(Q\) de l’ellipse avec la droite euclidienne \((AB)\) ne coupe l’ellipse qu’en ces deux points \(P\) et \(Q\). Toutefois il s’agit de l’intersection de deux coniques, soit un problème d’ordre 4. Le logiciel considère qu’il y a 4 intersections, et il convient de choisir les bonnes intersections. Nous détaillerons la méthode avec une illustration dynamique dans le cas 2. D’un point de vue dynamique il faut aussi conserver la droite euclidienne \((AB)\) quand celle-ci ne coupe pas l’ellipse (ou lui est tangent) car c’est alors la H-droite \((AB)\).
Configuration générale de Desargues non vérifiée
Prenons alors un triangle \(ABC\) dont les trois sommets sont extérieurs à l’ellipse. En utilisant les droites euclidiennes, par exemple la droite \((AB)\) et un point extérieur \(A_1\), on peut construire les parallèles euclidiennes à \((AB)\) passant par \(A_1\) et à \((AC)\) passant par \(A_1\). Sur la première on se donne un point \(B_1\), toujours extérieur à l’ellipse – car on ne sait tracer que ces droites – et on construit le troisième sommet \(C_1\) du triangle \(A_1B_1C_1\) dont les côtés sont parallèles à ceux de \(ABC\). On se place dans une configuration où \(C_1\) est lui aussi extérieur à l’ellipse. On peut alors construire les 9 H-droites de cette configuration affine de Desargues et vérifier que les droites \((AA_1), (BB_1), (CC_1)\) – vertes ci-contre -ne sont généralement pas concourantes, comme illustré ci-dessous à gauche, avec \((BC)\) la seule H-droite aussi euclidienne.
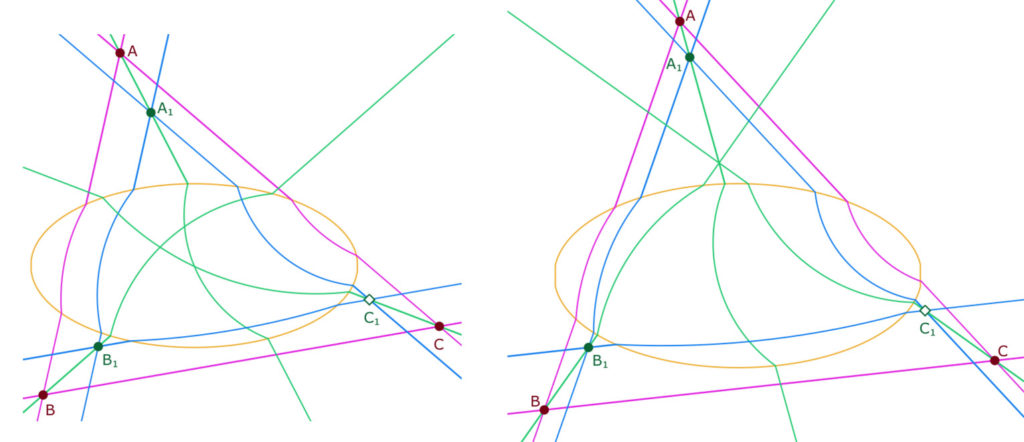
Bien entendu, si les trois H-droites \((AA_1), (BB_1), (CC_1)\) se coupent à l’extérieur de l’ellipse, elles sont concourantes car c’est le cas des droites euclidiennes support, puisque la configuration de Desargues est vraie dans le plan affine usuel. (Illustration de droite).
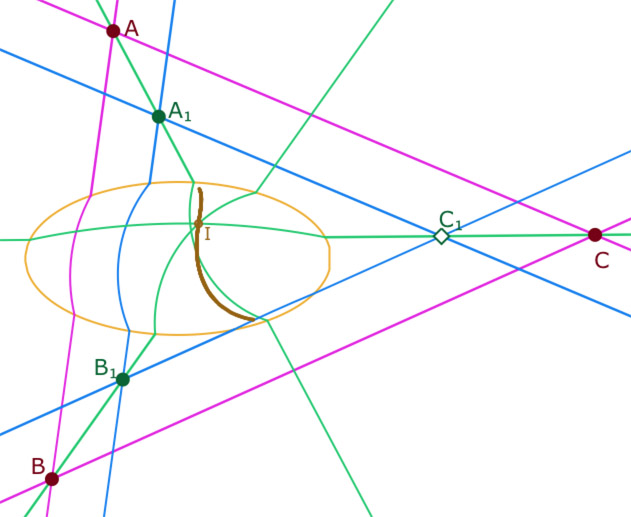
Ci-contre, \(I\) est l’intersection (dynamique) des H-droites \((BB_1)\) et \((CC_1)\). On a alors dessiné la trace du point \(I\) quand \(B_1\) décrit une partie de la H-parallèle à \((AB)\) passant par \(A_1\) du côté de \(B\), et tel que l’intersection soit à l’intérieur de l’ellipse.
On voit que cette trace coupe la H-droite \((AA_1)\). Cela illustre que, dans cette configuration, pour \(ABC\) et \(A_1\) donnés, il existe une position de \(B_1\) pour laquelle les trois H-droites vertes sont concourantes.
La question de la construction de cette position de \(B_1\) en fonction du triangle initial et de \(A_1\) est un premier questionnement (a priori non trivial) laissé au lecteur.
Manipulation de la première figure du modèle de Hilbert
Pour effacer la trace de I, recharger simplement la figure avec l’icone de l’iframe.
Premier exemple élémentaire
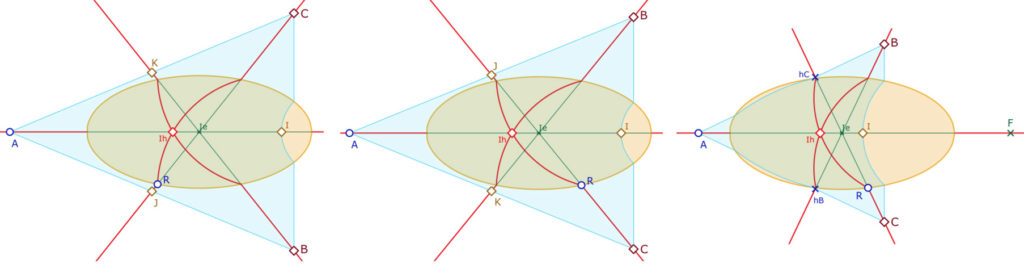
Même si, dans cette page, nous ne savons construire que des droites définies par deux points extérieurs à l’ellipse, il est possible d’explorer cette nouvelle géométrie non arguésienne dans cette situation bien particulière. En voici un premier exemple, celui des médianes. On se donne un triangle, tel que les sommets \(A, B, C\) et leurs milieux \(I, J, K\) sont tous extérieurs à l’ellipse. Si les médianes affines se coupent strictement à l’intérieur de l’ellipse, les H-médianes, vertes ci-dessous, ne sont généralement pas concourantes (à gauche). Par contre si les médianes affines sont concourantes hors de l’ellipse, c’est aussi le point de concours des H-médianes (au centre).
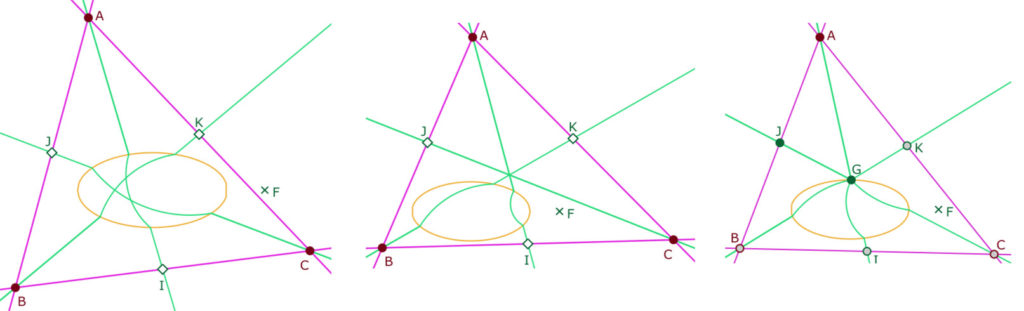
On peut s’amuser à construire (à droite) un triangle \(ABC\) dont les H-médianes sont concourantes en un point \(G\) de l’ellipse. Comme ce point \(G\) est à la fois le point de concours des H-médianes de \(ABC\) mais aussi des médianes affines de ce même triangle \(ABC\), on a construit – dans un cas très particulier, un triangle dont les médianes soient concourantes à la fois pour un triangle euclidien et pour le H-triangle associé.
A titre d’appropriation du modèle de Hilbert et des méthodes que l’on va développer par la suite, on se propose d’explorer cette possibilité dans un cadre un peu plus général et sur les différentes droites remarquables du triangle.
Droites bi-concourantes pour le triangle euclidien et le H-triangle
1 – constructions approchées
Ce paragraphe se propose d’explorer la possibilité de construire trois H-droites concourantes à l’intérieur de l’ellipse qui puissent être des droites remarquable du triangle associé. Pour construire ce triangle, on se donne comme principe de résolution – en particulier pour les médianes exemple détaillé ci-dessous – que les droites affines associées soient aussi concourantes. L’approche ici est seulement heuristique, on cherche simplement à approcher ces solutions. L’objectif est de continuer à se familiariser à ces nouvelles configurations et de construire des représentations riches.
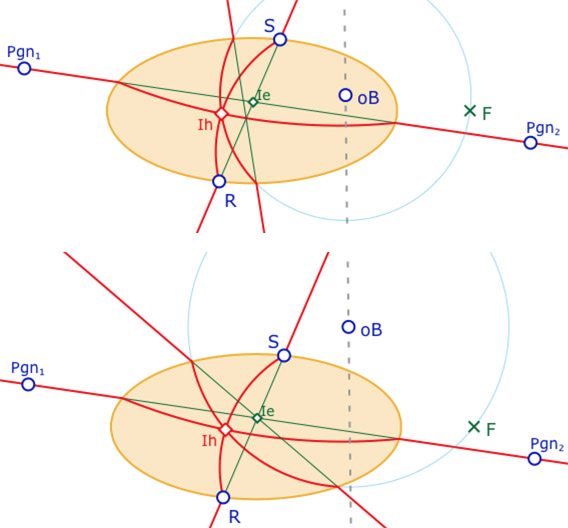
On se donne deux poignées, \(Pgn_1\) et \(Pgn_2\) d’une H-droite qui contiendra le sommet \(A\) du triangle. Deux points de l’ellipse, \(R\) et \(S\) construisent une autre droite. Elle contiendra le sommet \(B\). Les deux H-droites associées se coupent en \(I_h\) (\(h\) pour le modèle de Hilbert). Les deux droites euclidiennes associées (vertes ci-conte) se coupent en \(I_e\) (\(e\) pour le modèle euclidien). Dire que le triangle \(ABC\) a ses trois H-droites remarquables concourantes, signifie que la troisième H-droite passe aussi par \(I_h\). Mais puisque le triangle \(ABC\) a ses sommets extérieurs à l’ellipse, comme triangle euclidien, les droites euclidiennes support des H-droites sont – doivent – elles aussi concourantes, ce qui n’est pas vrai en général (illustration du haut). Il y a deux choix possibles pour une construction exploratoire :
• soit la troisième H-droite est une vraie H-droite – au sens où son cercle support passe par \(F\), et alors son centre est piloté par un point \(oB\) sur la médiatrice de \(I_h\) et \(F\). Dans ce cas on choisit à la main \(oB\) pour que la troisième droite euclidienne passe par \(I_e\) (seconde illustration ci-contre). Le point de concours euclidien des «droites remarquables» sera approximatif et donc les vérifications euclidiennes le seront aussi.
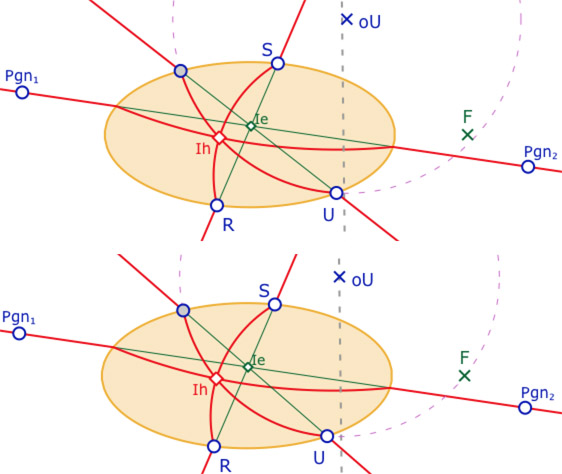
• soit on se donne un autre point de l’ellipse – le point \(U\) ci-contre, et on construit l’arc de cercle tel que la troisième droite euclidienne passe par \(I_e\). Alors cet arc de cercle n’est, en général, pas celui d’une H-droite, le cercle euclidien associé ne passe pas par \(I_e\), ou encore son centre \(oU\) n’est pas sur la médiatrice de \(I_h\) et \(F\) (ci-contre aussi). Il faut alors agir sur ce nouveau point \(U\) pour que le cercle associé passe par \(F\) (seconde illustration).
Dans cette approche de la construction, les éventuelles vérifications euclidiennes seront toujours exactes – donc inutiles à faire, mais la troisième droite du modèle – ici celle contenant \(B\), se sera pas « tout à fait » une H-droite.Dans la suite on a choisi la première option, la vérification des mesures permettant aussi d’affiner les réglages de la figure.
Mise en œuvre de cette option
Les droites étant concourantes, on se donne un sommet \(A\) de la première droite, celle avec les deux poignées. On peut alors utiliser les constructions classiques pour construire le triangle \(ABC\) tel que ces trois droites soient, respectivement, les médianes, les hauteurs ou les bissectrices. Dans le premier exemple avec les médianes, la figure n’a de sens que si les sommets \(A, B, C\) et les milieux \(I, J, K\) sont tous hors de l’ellipse. Pour cela, il suffit d’éloigner \(A\) de l’ellipse.
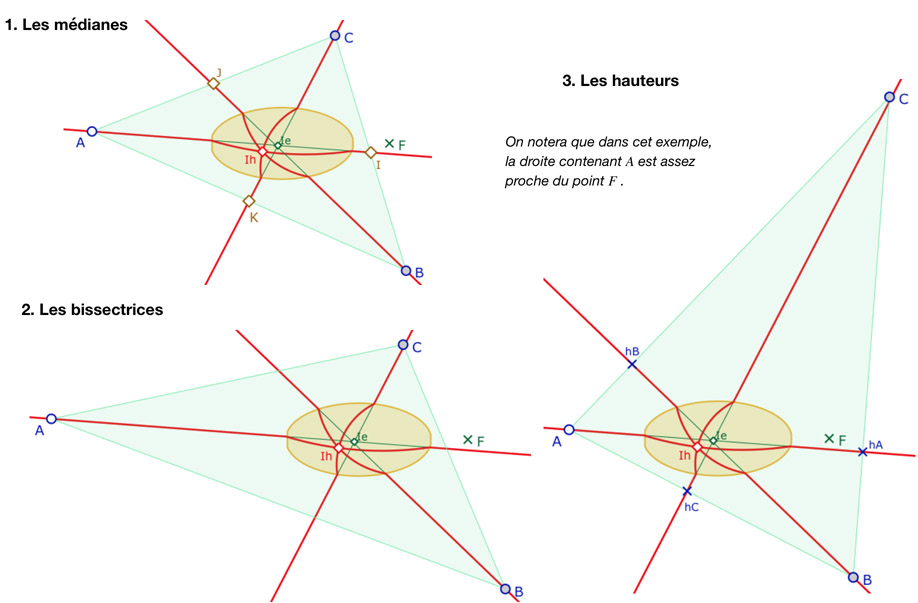

Illustration avec les vérifications euclidiennes associées
C’est aussi l’occasion de voir les différentes options de la prochaine figure.
Les médianes
Par construction \(J\) et \(K\) sont les milieux et ils sont sur les H-droites. L’approximation, liée à celle du concours des droites euclidiennes, porte sur le point \(I\) , qui par construction, est sur la H-droite passant par \(A\) mais n’est pas tout à fait le milieu de \(B\) et \(C\) … mais on atteint facilement la précision au millième.
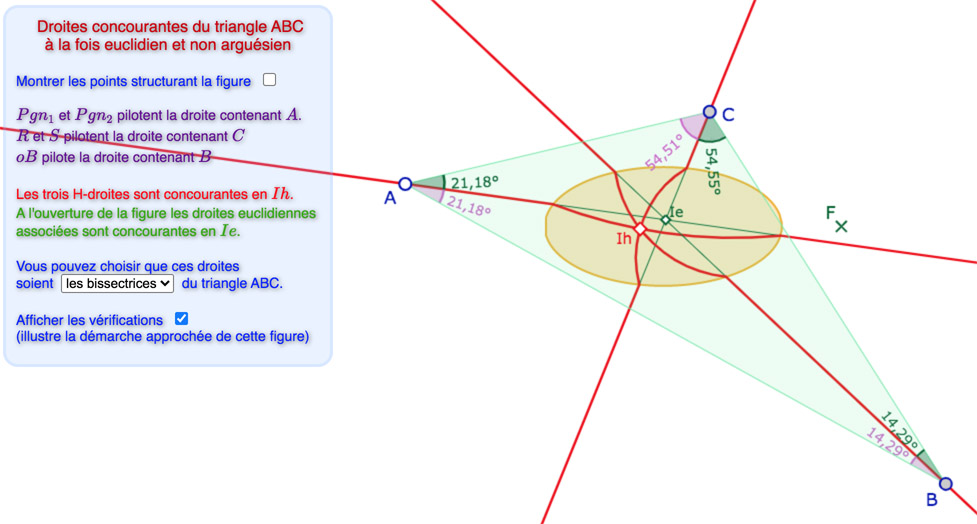
Les bissectrices
Par construction les bissectrices sont exactes en \(A\) et \(B\). La construction de \(C\) est aussi exacte d’un point de vue euclidien, mais \(C\) n’est pas tout à fait sur la H-droite qui doit la contenir, d’où des angles non égaux en \(C\), selon les choix de mesure.
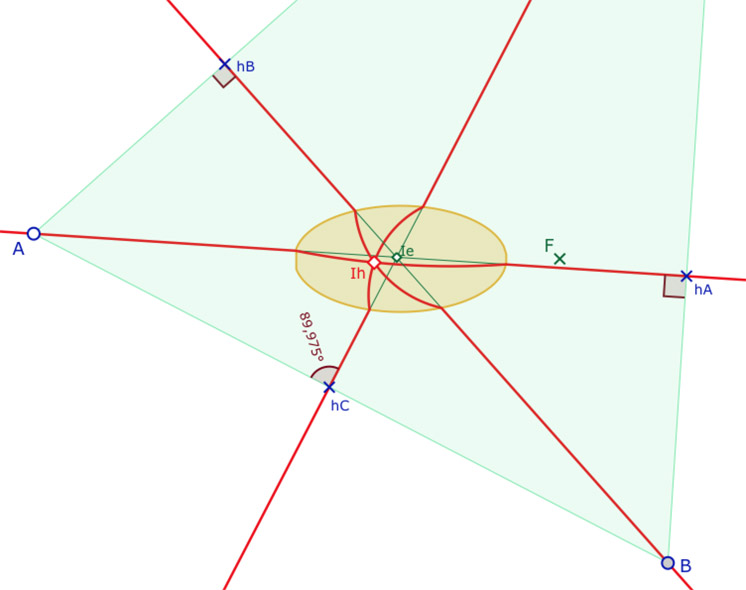
Les hauteurs
Par construction, les hauteurs issues de \(A\) et de \(B\) sont exactes, d’où les angles droits. L’approximation de la figure se porte sur la hauteur issue de \(C\) et donc l’angle en son pied qui n’est pas tout à fait droit.
Autre exemple (droite des poignées plus éloignée de \(F\))
Sur l’illustration ci-dessous, on a utilisé les vérifications numériques pour piloter les points de base afin d’affiner la précision de la figure en se réglant sur celles des angles ou des longueurs. La configuration est différente, on voit que les trois droites ont des pentes différentes.
L’angle en \(h_C\) est proche de 90° (90,006°).
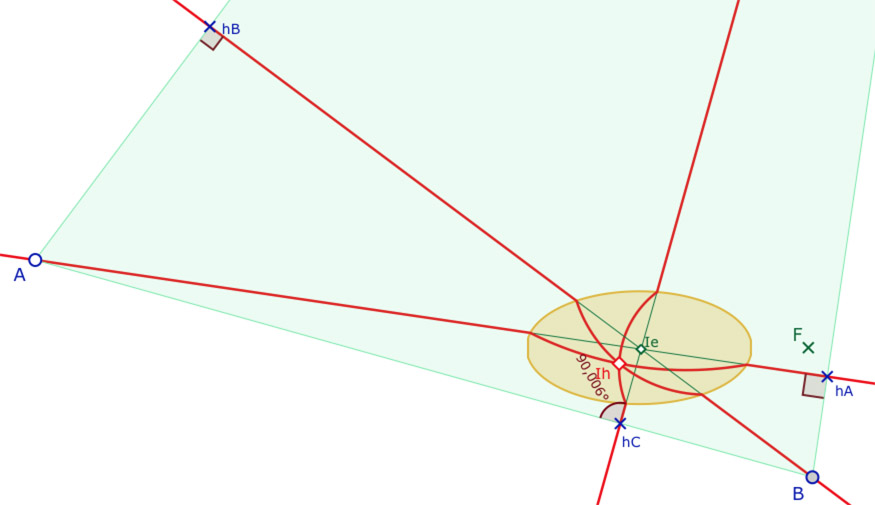
Figure associée sur les droites remarquables bi-concourantes d’un (et d’un H-) triangle extérieur à l’ellipse
Mode d’emploi
1.Activer les points de base de la figure (la case à cocher).
2.Modifier la configuration (par les poignées \(Pgn_1, Pgn_2\), et les points \(R\) et\(S\)).
Attention : la poignée de gauche est dans le widget : il faut déplacer le widget. (éventuellement travailler en plein écran)
3.Puis agir sur le centre du cercle \(oB\) pour que la 3° droite passe par \(I_e\).
4. Choisir ensuite le type de droite et agir sur \(A\) pour choisir la taille de la figure.
Rappel : on peut déplacer la figure dans la page, au doigt ou à la souris.
On peut utiliser aussi cette figure en plein écran, dans un autre onglet, sans l’environnement « responsive ». Penser à désactiver la flèche gauche du tableau de bord pour être en mode consultation.
2 – Exemples de constructions exactes de la même
propriété dans un cas particulier
Dans la figure précédente, le réglage dynamique du point \(oB\) pour que les droites euclidiennes soient concourantes en \(I_e\) pourra se faire avec la technique qui sera utilisée plus loin pour la droite générale (programmation par dichotomie). En attendant on peut réaliser des constructions exactes géométriques dans un cas bien particulier, celui où \(I_e\) est l’origine du repère, c’est-à-dire le centre de l’ellipse. Commençons par un cas statique : le cas bi-équilatéral.
Tout d’abord on se donne comme première H-droite, l’axe des abscisses (car toute droite passant par \(F\) est une H-droite). En l’origine \(I_e\), on se donne deux droites à 60°, on construit les H-droites associées. A partir d’un point \(A\) de l’axe des abscisses, on construit un triangle \(ABC\) avec les sommets sur les H-droites tel que les droites soient les médianes. Si les côtés du triangle sont entièrement extérieur à l’ellipse, il est clair que \(ABC\), euclidien, est aussi H-équilatéral et les H-droites rouges sont à la la fois les H-médianes, les H-hauteurs et les H-bissectrices du H-triangle \(ABC\) alors que les droites euclidiennes associées sont les hauteurs, médianes et bissectrice du triangle (aussi) euclidien \(ABC\). (illustration de gauche)
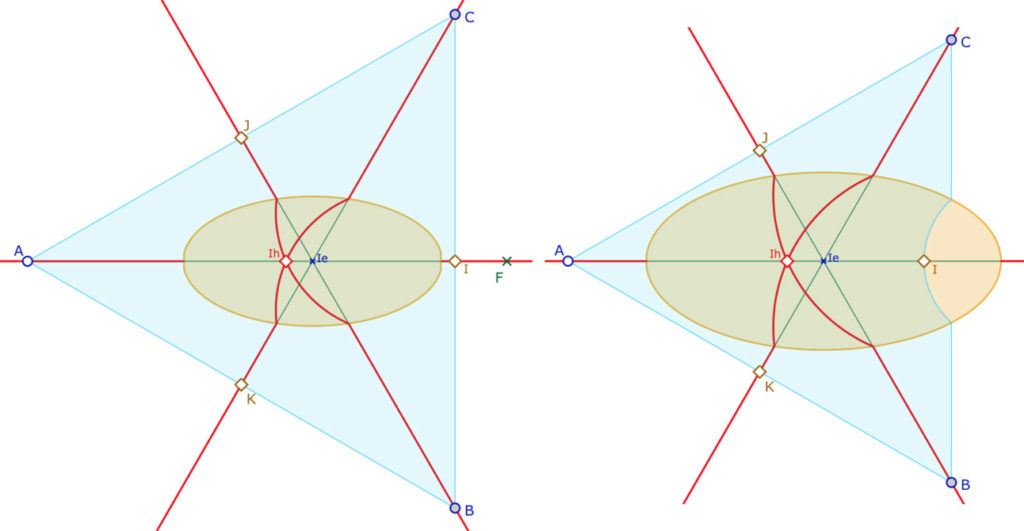
On peut aller un peu plus loin. Puisque, par construction \((BC)\) est orthogonal à \((AF)\), si la droite \((BC)\) coupe l’ellipse, on construit la H-droite \((BC)\) comme ci-dessus à droite. Alors le point \(I\) est toujours milieu de \([BC]\) (par symétrie) ainsi que le pied de la hauteur issue de \(A\). Le H-triangle \(ABC\) n’est plus équilatéral mais seulement isocèle. Et pourtant les trois angles sont égaux, et ses trois H-droites remarquables sont encore à la fois médianes, hauteurs, et bissectrices de \(ABC\).
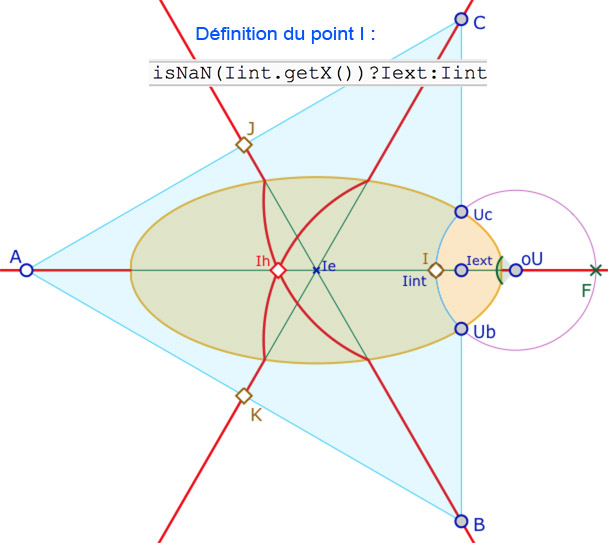
Détails techniques pour colorier l’intérieur du H-triangle dynamiquement, selon sa forme
On définit le point \(I\) comme étant l’un des deux points \(Iint\), si \((BC)\) coupe l’ellipse, ou \(Iext\) , le milieu de \(B\) et \(C\), sinon. Puis on créé une liste de segments que l’on construit par programmation Blockly. Ici sa représentation graphique se note \(l_1\).
Si \(I\) est extérieur à l’ellipse, la liste est seulement \([A,C,B,A]\), sinon on parcours l’arc de cercle allant de \(Uc\) à \(Ub\) en utilisant son centre \(oU\) et son angle \(aU\).
La programmation est élémentaire dans ce cas. Elle est proposée pour le principe : on travaille sur une expression (en pratique, une liste de segments) et on notifie les aspects de sa représentation graphique.
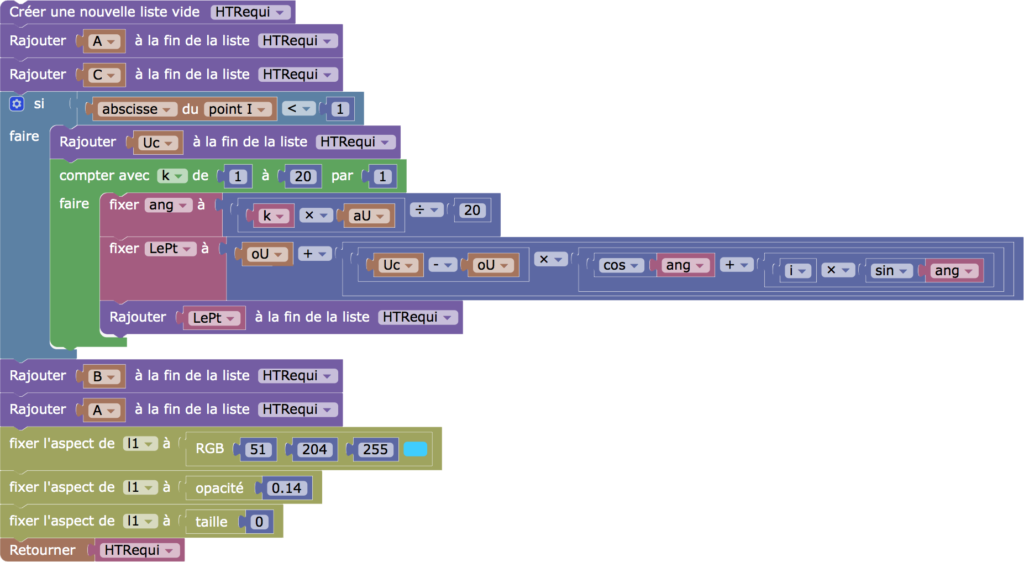
La taille à 0 (aspect de l1) est celle des points constituant la liste : ici on lisse en cachant les points.
Extension dynamique de la figure précédente
Toujours dans l’optique de réaliser une construction exacte, on conserve comme point de concours des droites remarquables du triangle euclidien l’origine du repère, centre de l’ellipse (toujours noté \(I_e\)). On se donner désormais un point \(R\) de l’ellipse qui détermine les deux autre H-droites (que l’axe des abscisses) symétriques qui permet de construire le H-triangle \(ABC\) et le triangle euclidien associé, quand celui-ci est différent.
Exemple des médianes
C’est en particulier les illustrations comme celle du centre ci-dessus, quand les droites sont les médianes, et le milieu \(I\) du H-segment \([BC]\) est intérieur à l’ellipse. On notera que, comme le sommet \(C\) est sur la H-droite pilotée par le point \(R\), selon la position de \(R\), par rapport au centre de l’ellipse, \(C\) est au dessus ou en dessous de l’axe des abscisses.Rappelons que, dans le cas des médianes, a priori la construction n’a de sens que si le segment euclidien \([AB]\) ne coupe pas l’ellipse.
Exemple des hauteurs
Par contre, pour les hauteurs, on peut aller un peu plus loin : même si le segment \([AB]\) coupe l’ellipse, on peut étendre la construction tant que les pieds des hauteurs \(h_B\) et \(h_C\) sont extérieurs à l’ellipse, ce qui peut donner un triangle avec un arc sur chaque segment à l’intérieur de l’ellipse comme ci-dessus à droite. Le point \(I\) est bien entendu aussi le pied \(h_A\) de la hauteur issue de \(A\). Le triangle euclidien \(ABC\) et le H-triangle associé sont alors bien différents, mais ils ont toujours, comme point de concours des hauteurs, respectivement les points \(I_e\) et \(I_h\).
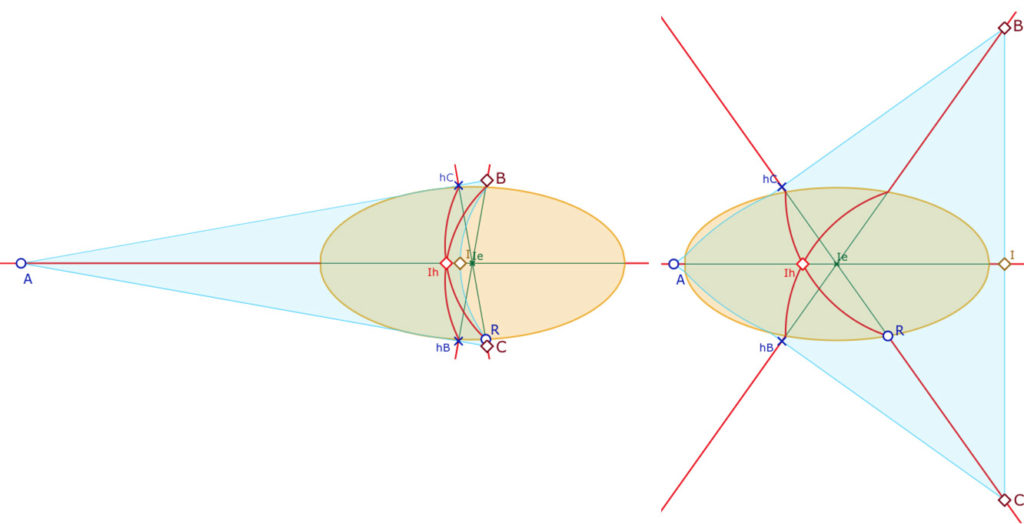
Deux autres exemple de hauteurs : à gauche avec \(I\) entre les centres \(I_e\) et \(I_h\), à droite avec I extérieur à l’ellipse.
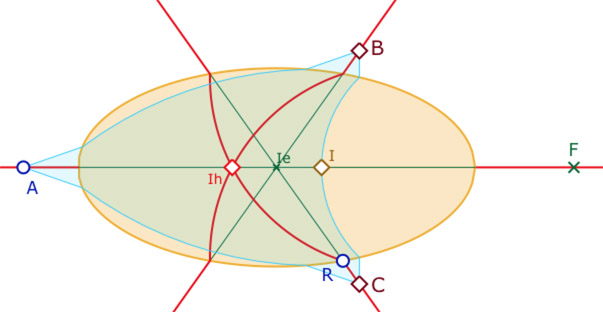
Exemple avec les bissectrices
Là encore, la construction est exacte, même si les formes des H-triangles peuvent surprendre dans un premier temps. Bien entendu, la figure n’a de sens que si les points \(B\) et \(C\) sont extérieurs à l’ellipse.
Dans la figure suivante, on choisit le type de H-droites, on peut agir sur \(A\) et \(R\).
Un message apparait si la construction perd son sens, et le H-triangle disparait.
Manipulation de la figure associée avec les bi-médianes, bi-hauteurs ou bi-bissectrices exactes
On peut aussi lancer la même figure (non restreinte) dans un onglet en pleine page.
3 – Retour sur le triangle équilatéral
réalisé par programmation Blockly
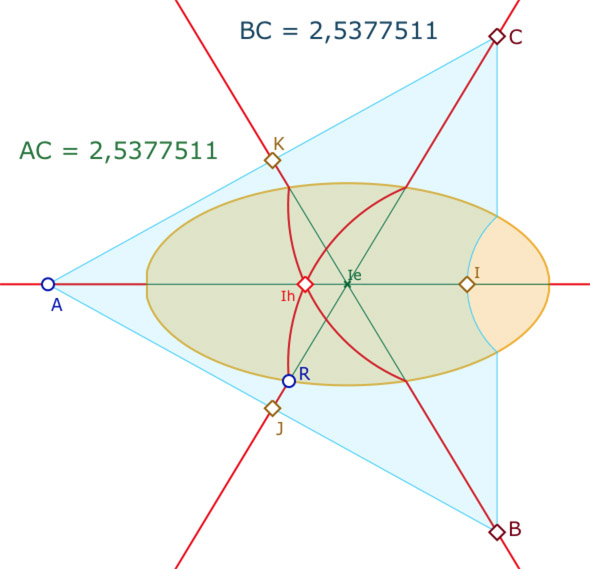
Dans ce que l’on a fait précédemment, les triangle sont toujours isocèles puisque \(AB=AC\) par construction. Mais peut-on avoir l’égalité des trois côtés, et en particulier quand \(I\) est à l’intérieur de l’ellipse comme ci-contre ?
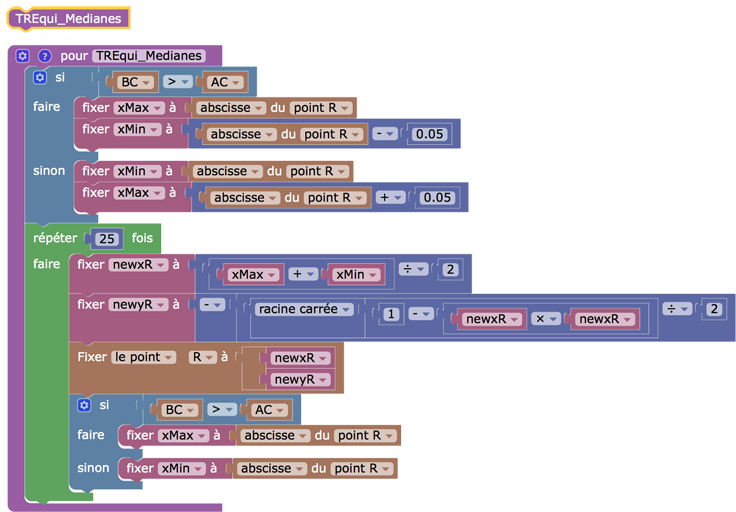
Si on cherche à effectuer les calculs on trouve une équation trigonométrique qui ne peut être résolue que par approximation. Aussi autant chercher directement une approximation sur la figure. Voici la version élémentaire du code Blockly, par dichotomie, et, pour plus de lisibilité, pour le cas de la médiane seulement.
On notera la marge de 0,05 que l’on se donne en variation d’abscisse pour \(R\). Cela signifie que le programme doit être lancé proche d’une solution (quand les longueurs sont proche à \(10^{-1}\)). C’est la grande force de la «programmation par comportement» du Blockly de DGPad : on programme, sur le point \(R\), des modifications sur lui-même en fonction de données actualisées de son environnement : les longueurs \(BC\) et \(AC\).
On peut bien sûr étendre un peu plus la démarche pour chercher des H-triangles équilatéraux avec trois arcs de cercle euclidiens, dont les droites initiales (rouges) soient les hauteurs. Ci-dessous à droite, on détaille l’expression de la longueur \(BC\) (utilisée dans la figure précédente), et celle de la longueur \(AC\).
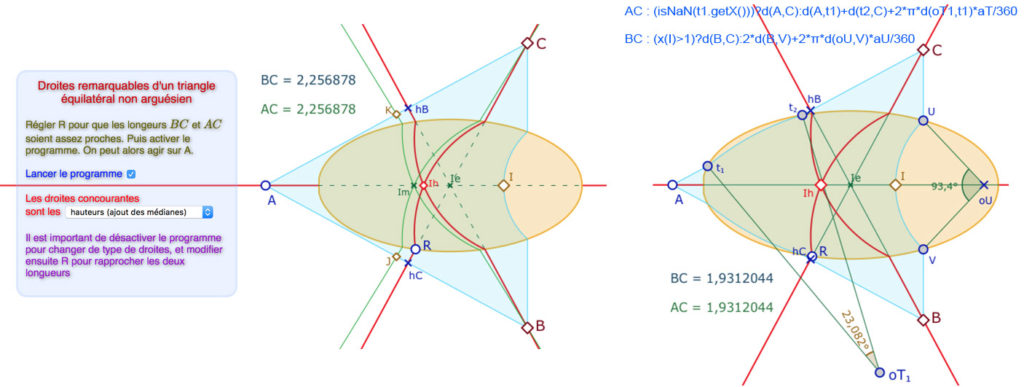
Dans l’illustration de gauche ci-dessus, le (nouveau) programme de la prochaine figure, appliqué aux hauteurs donne le H-triangle \(ABC\) tel que \(I_h\) soit l’orthocentre du triangle. On a ajouté (en vert) les médianes du triangle (\(I\) est à la fois le milieu et le pied de la hauteur issue de \(A\)). Elles sont concourantes en \(I_m \neq I_h\). Le H-triangle \(ABC\) est équilatéral tel que ses hauteurs sont concourantes ainsi que ses médianes, mais ces droites ne sont pas confondues.
Voici une nouvelle illustration avec les H-médianes, ci-dessous à gauche. Le programme construit \(ABC\) équilatéral tel que les médianes sont concourantes en \(I_h\). On a ajouté, en bleu, les hauteurs. Elles sont concourantes en \(I_{h_2} \neq I_h\). On a donc un autre triangle équilatéral avec les hauteurs et les médianes non confondues. Quand on s’intéresse au couple «médianes-hauteurs» il faut que \(K\) et \(J\) soient extérieurs à l’ellipse. Les triangles n’ont donc qu’un côté avec un arc de cercle.
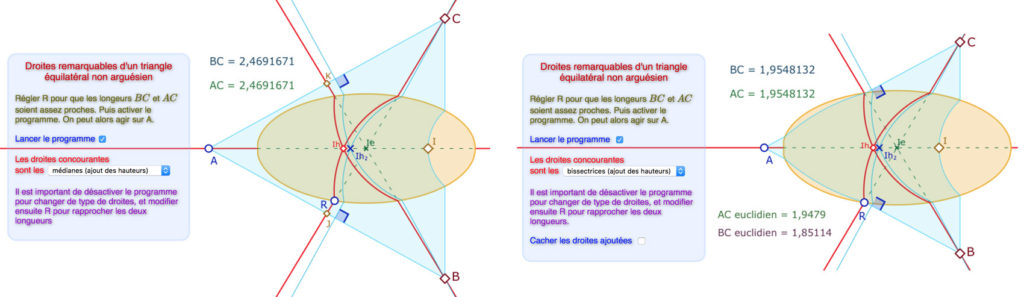
A droite, un exemple avec le triangle \(ABC\) construit depuis les bissectrices. On y a ajouté aussi les hauteurs. Le cas avec les bissectrice est plus général qu’avec les médianes car il n’y a pas de milieu à calculer, les trois côtés peuvent couper l’ellipse et avoir, chacun une partie en arc de cercle. Il faut bien entendu que les pieds des hauteurs soient extérieurs à l’ellipse pour que cette figure soit correcte.On voit qu’ici aussi, le H-triangle équilatéral \(ABC\) a ses bissectrices et ses hauteurs concourantes mais en des points différents.
Manipulation de la figure : triangle équilatéral construit à partir de ses droites remarquables.
La figure précédente est une figure restreinte. Si on veut consulter le code du programme, toujours placé dans le point R, il faut utiliser cette autre figure en ligne (sans restriction), activer le mode standard (flèche sélectionnée) … et avoir déjà pratiqué le Blockly de DGPad.
Cette figure achève notre toute première exploration des droites du modèle de Hilbert. Rappelons que jusqu’ici nous ne savons construire, et utiliser, que les droites définies par deux points extérieurs à l’ellipse.