La seule chose à savoir pour réaliser les figures de cette page est le rayon du cercle de pavage. Il vérifie \(ch38= ch(r_{38})= \displaystyle \frac{1}{\sqrt{6}-\sqrt{3}} \). Cet article de blog traite du calcul d rayons des cercles de pavage.
Ceci étant donné, la construction se fait comme à la page précédente. On arrive ainsi à un premier triangle équilatéral d’angle au sommet de 45° que l’on peut manipuler dans la figure suivante
Comme pour les triangles uniques de la page précédente, ne pas hésiter à manipuler tous les paramètres
Préférer lancer la figure dans un nouvel onglet
Illustration de présentation de la figure P(3,8)
Comme les angles au sommet sont de 45° on peut optimiser la figure en n’utilisant la polaire que d’une droite sur deux. On peut aussi – c’est ce que l’on a fait dans un premier temps – utiliser cette possibilités pour construire un point sur deux de deux façons différentes (avec l’orthogonalité et sans) et avoir ainsi une vérification que la figure est correcte.
Avec 8 triangles autour d’un point on peut jouer avec les paramètres d’affichage de la figure finale. Voici des illustrations de quelques possibilités
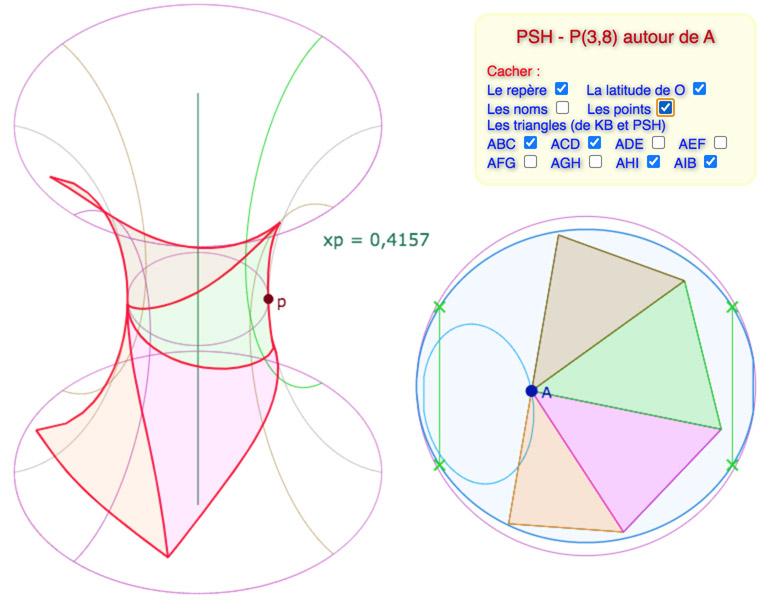
Quatre triangles équilatéraux de 45° dans une configuration plus « verticale » sur la PSH.
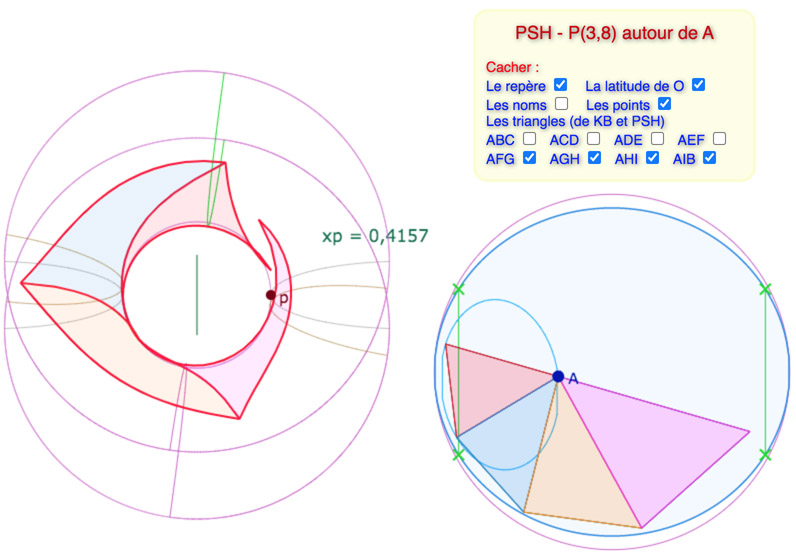
Autre configuration de quatre triangles du pavage dans une vue de dessus.
On voit clairement sur la PSH que l’ensemble fait un peu plus d’un tour
Mais peut jouer aussi à des configurations plus aérées comme celle-ci en « ailes de moulin »
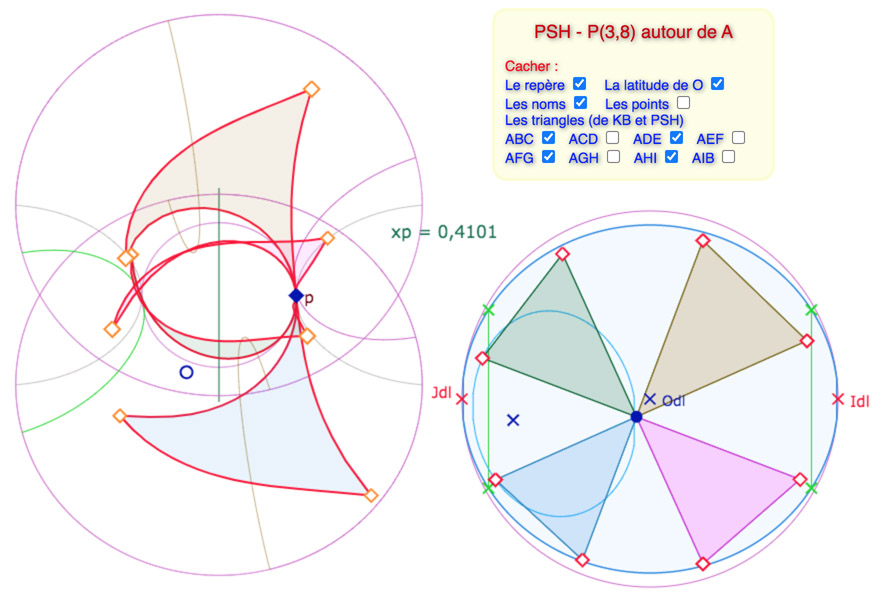
On remarque sur cette illustration, que contrairement aux pavages P54 et P45, on peut garder les huit triangles entièrement sur la pseudosphère hyperbolique tout en prenant le centre du cercle de pavage assez loin de la frontière de la feuille principale, alors que pour les pavages précédents, il devait être presque collé au méridien vert de la frontière.
Ou encore cette configuration que l’on dira « du papillon »
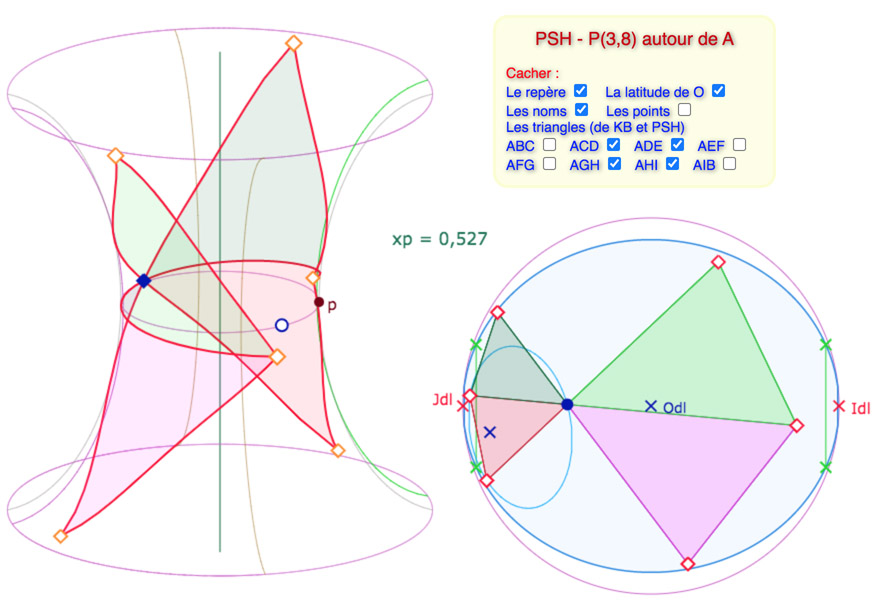
On remarquera, ci-dessous, que le centre \(O\) du cercle est au delà de la longitude nulle (milieu de la feuille principale).
En agissant sur la latitude \(u_O\) et sur le point \(A\), le pavage rentre sur la surface et même, selon la valeur de \(x_p\), entièrement sur la feuille principale (ici non car on a voulu illustrer la grande mobilité du centre du cercle).
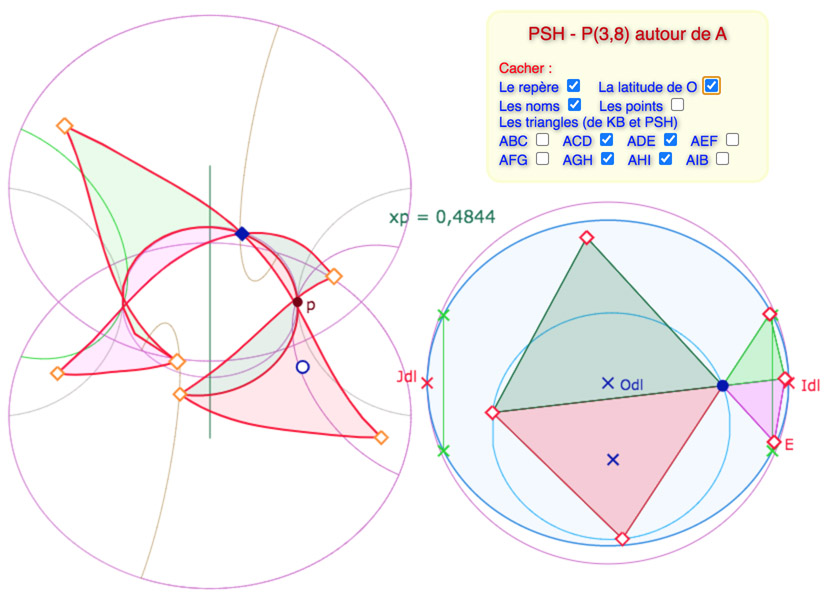
Enfin une illustration avec les huit triangles affichés

La figure à manipuler
Mêmes remarques – consignes – qu’à la figure de la page précédente.
Pour explorer les différentes possibilités de ce (début de) pavage P(3,8)
Préférer lancer la figure dans un nouvel onglet, ou encore utiliser cette version ou les segments sur la PSH sont à densité 40 au lieu de 20 pour la figure précédente.
Construction autour du pavage P(8,3)
Cette partie est l’occasion de belles illustrations, un peu imprévues, car il rentre plus d’octogones que « prévu »sur la PSH. Tout d’abord le classique octogone seul (donc de 120°).
Préférer ouvrir la figure dans un nouvel onglet.
Première illustrations autour du pavage P(3,8)
On commence par le pavage lui-même, soit trois octogone autour d’un point … même si c’est un peu déconcertant.
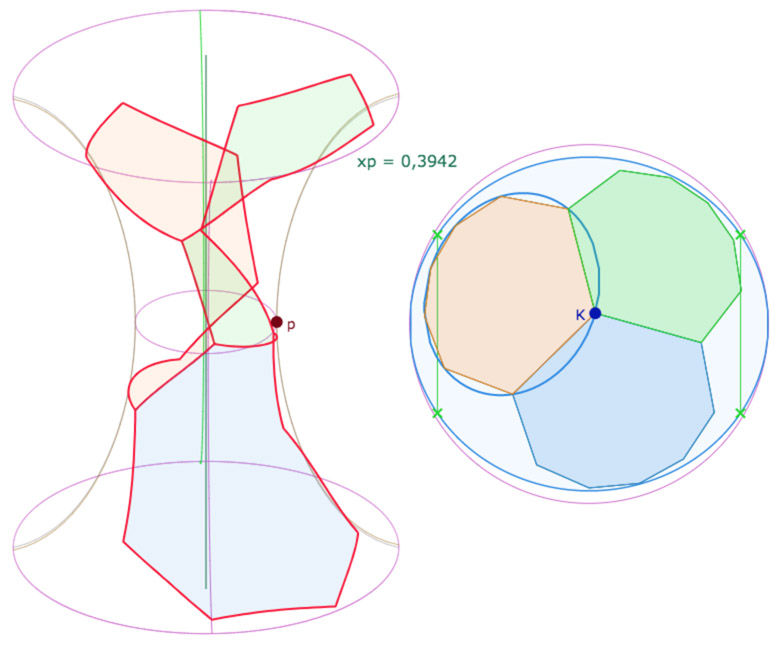
D’abord une vue de face, ensuite une vue de dessus : on voit peut-être mieux le chevauchement des octogones
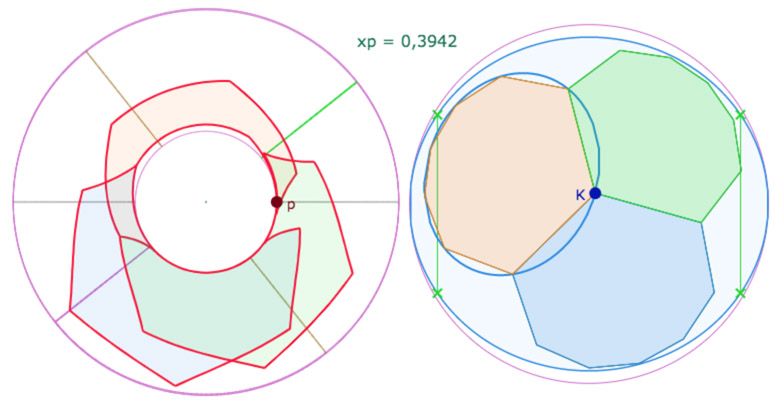
On poursuit par la vue de deux des trois octogones dans la configuration géométrique précédente
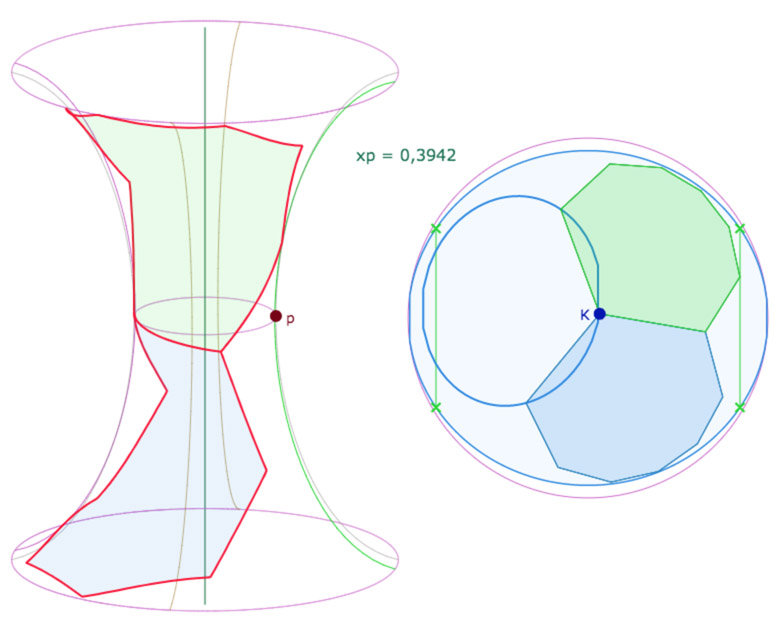
Placer un quatrième octogone dans P(8,3)
On voir bien que pour certains réglages, il peut y avoir « de la place sur la PSH » pour un quatrième octogone, on y consacre donc cette section. On propose ici une illustration détaillée en prenant les octogones deux par deux.
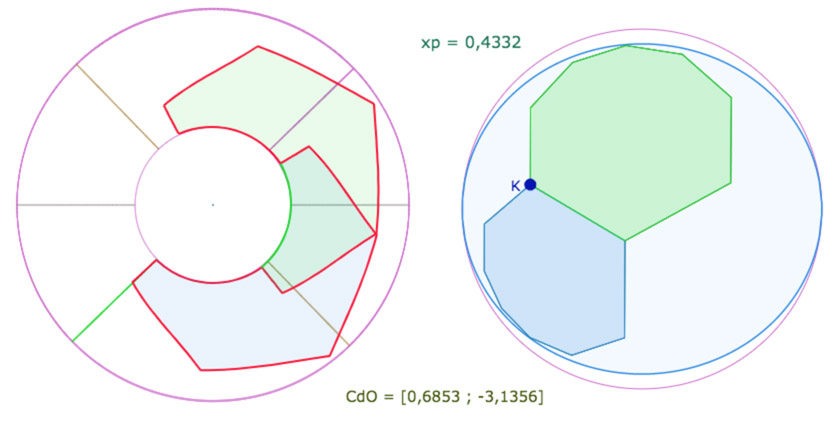
On notera plusieurs choses sur cette illustration. Tout d’abord, même s’il n’apparaît pas, on lit sur sa longitude que le centre du cercle de pavage est sur la feuille principale mais à sa toute limite inférieure puisque sa longitude est très proche (pour la manipulation à la souris en tout cas) de la valeur extrémale de \(-\pi\).
On remarquera aussi qu’un côté de l’hexagone bleu est quasiment sur le méridien vert de la frontière de la feuille principale. On a colorié aussi en vert le segment issu de \(K\), commun aux hexagones bleu et vert. Ci dessous la même configuration de face.
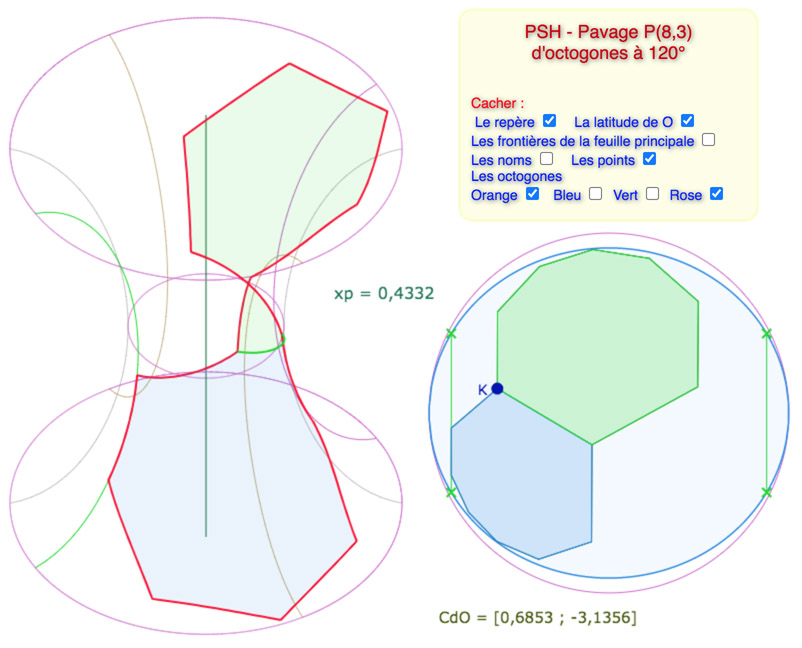
Ajout d’un quatrième octogone, à droite – sur KB – du bleu
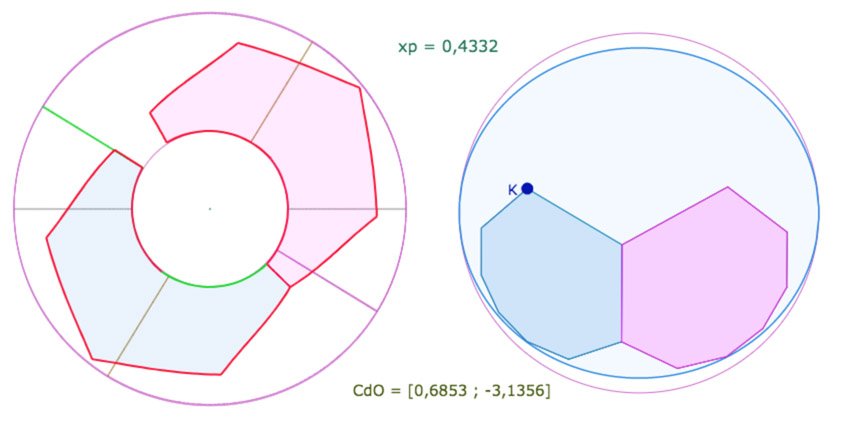
On note les mêmes repères, le côté vert de l’octogone bleu (qui bizarrement ne se voit pas sur KB) et le côté de l’octogone (vertical sur KB) qui est sur le méridien frontière vert.
Et sur l’illustration ci-dessous, on remarque qu’un des sommets de l’octogone initial orange (celui piloté par le point \(K\)) est proche du même méridien vert.
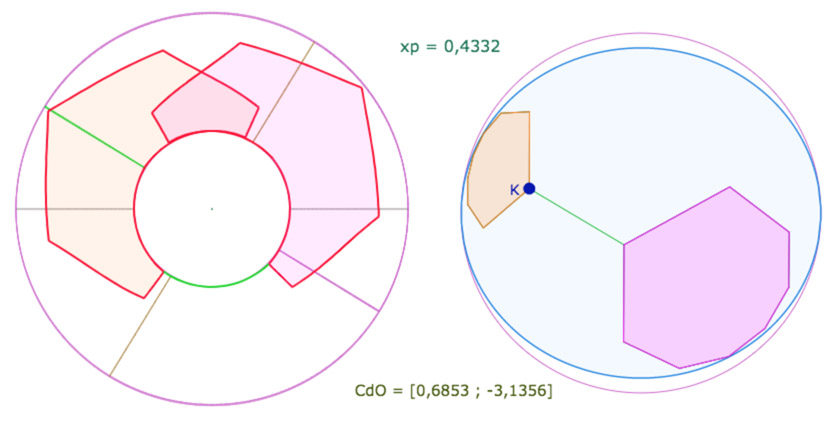
Ce qui est intéressant c’est la même configuration de face
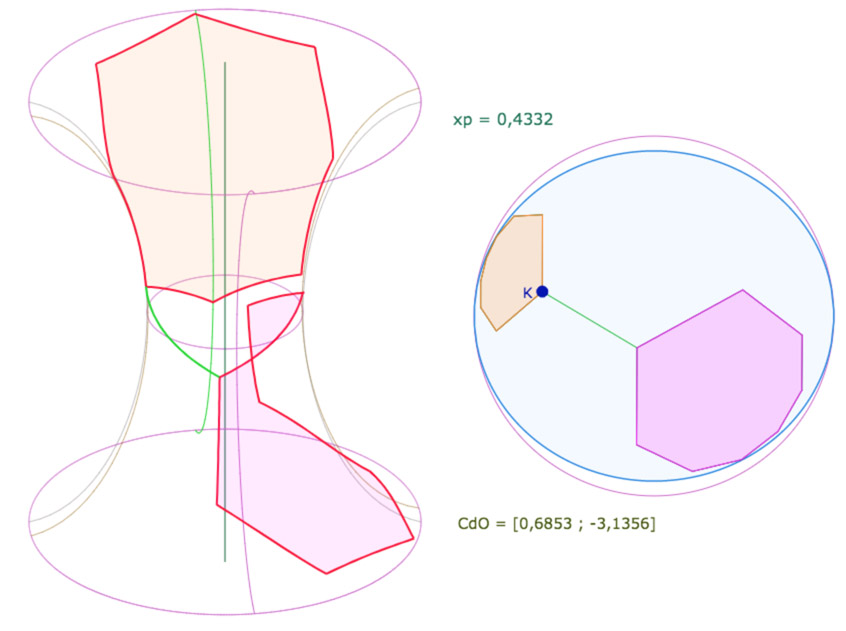
Et enfin les quatre octogones ensemble, toujours dans la même configuration, vus de face
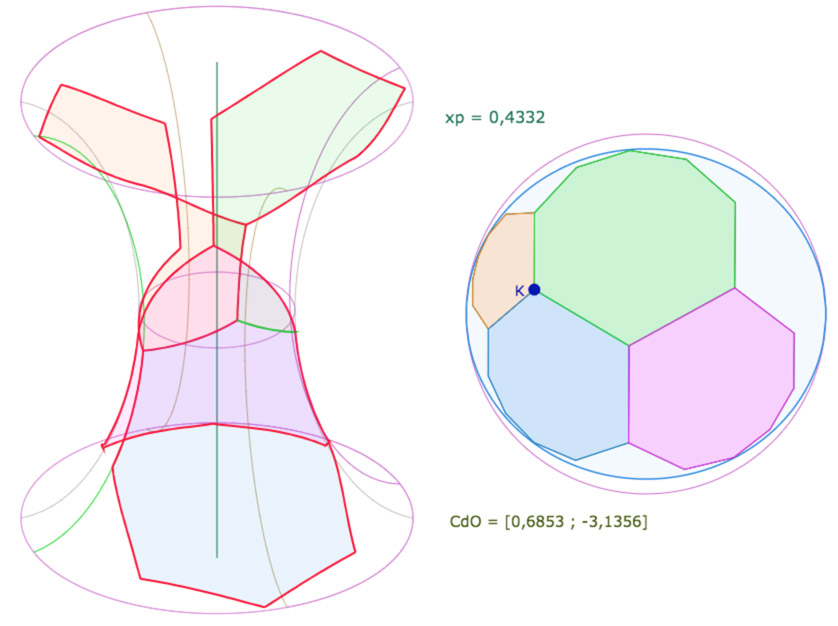
Et de dessus (trop joli)
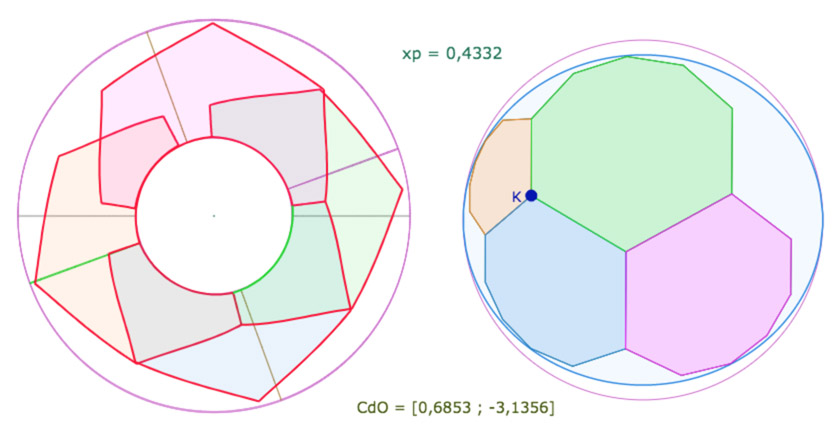
Ouvrir la figure de cette configuration dans un nouvel onglet (être en mode consultation, sans outil sélectionné)
Les octogones orange et rose dans d’autres règlages – en particulier d’autres valeurs de \(P\)
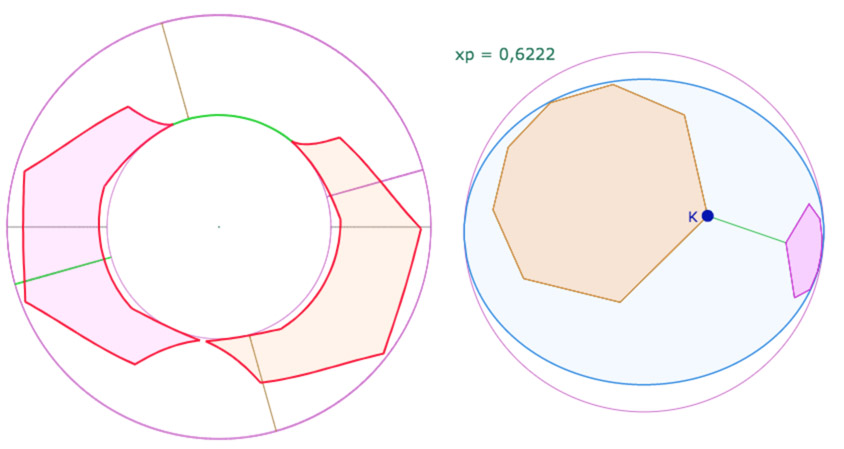
Illustration de l’illusion du contact : ils sont au contraire à une différence de l’ordre d’un demi-tour
(il faut faire tourner la PSH pour mieux voir ce qu’il en est)
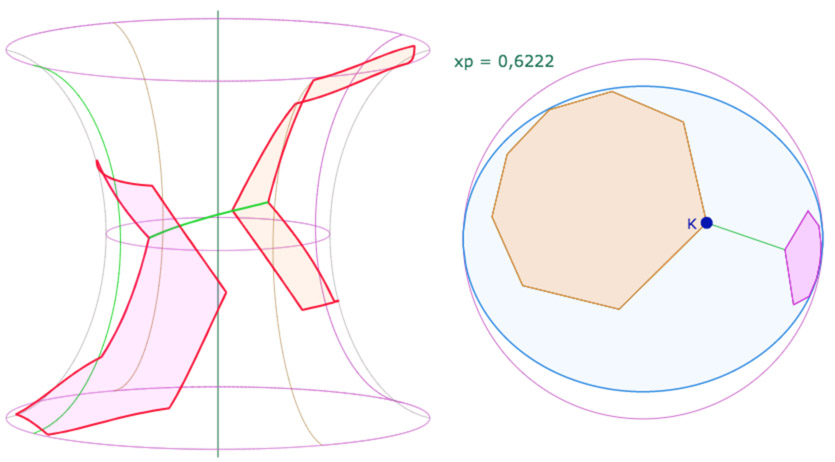
Autre situation
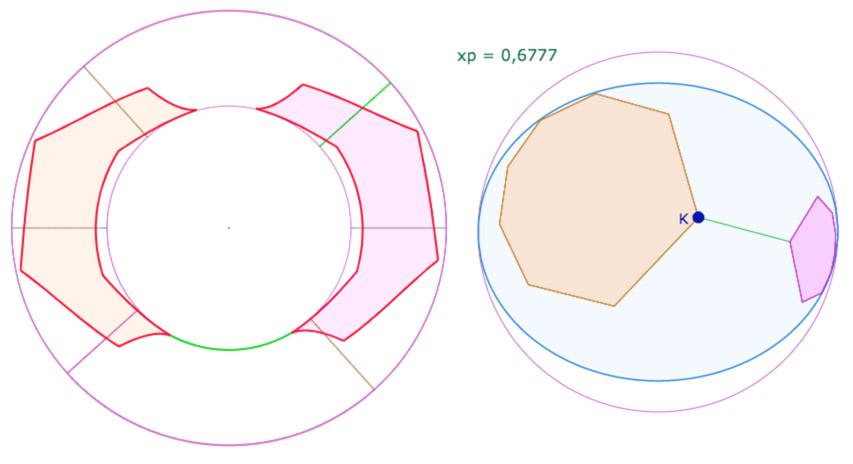
Cette fois-ci ils sont bien face à face …
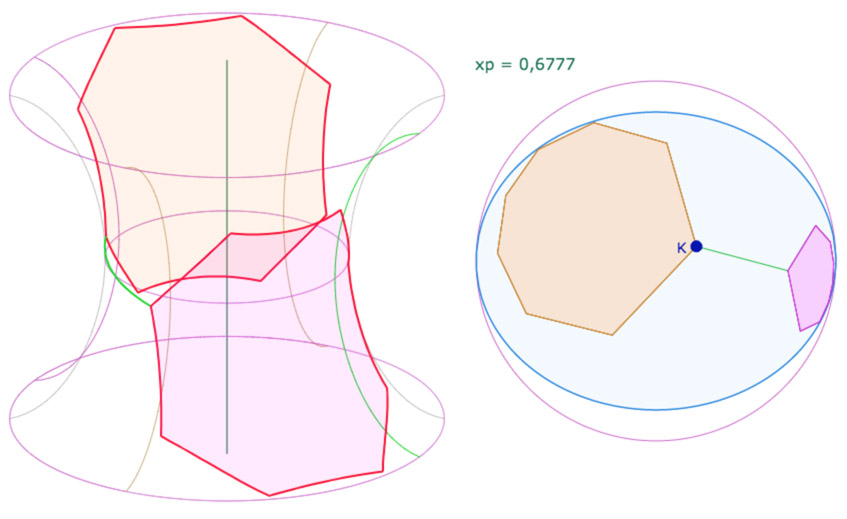
Ouvrir la figure de cette configuration dans un nouvel onglet (être en mode consultation, sans outil sélectionné)
Enfin un cas avec une PSH plus resserrée
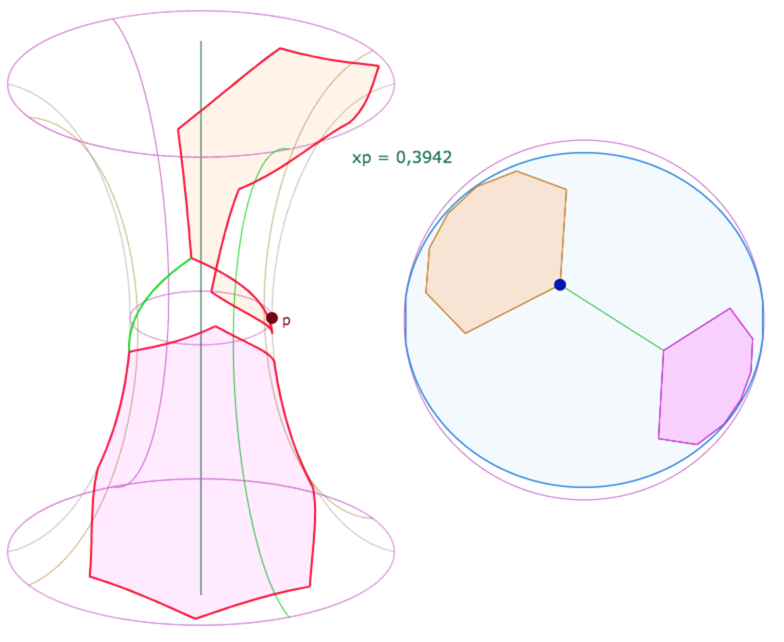
On n’a pas placé cette figure dans une iframe, car il suffit d’ouvrir une des deux figures proposées ci-dessus pour explorer toutes les situations possibles. On notera que dans ce cas le centre du cercle est toujours sur a feuille principale.