Comme déjà mentionné en introduction dans ce menu, Beltrami était surtout centré sur la validation de la géométrie de Lobatchevsky par sa réalisation concrète, matérielle, physique sur une surface euclidienne, et donc sur les surfaces pseudosphériques, plus particulièrement. En pratique, il n’a pas vu, avant la parution de son article, que ses figures intermédiaires, dans son « disque-limite », étaient déjà en soi celles d’un modèle du plan hyperbolique. À cette époque, Klein étudiait une généralisation de la théorie de la conique absolue de Cayley – encore inconnue de Beltrami – et cherchait à inclure de cette façon toutes les géométries dans une géométrie projective métrique. Il y parviendra totalement en 1871. Et sous ses yeux, ce qui n’était au départ qu’un artifice de représentation pour Beltrami va devenir tout de suite – quelques mois après la publication du « Saggio … » – un modèle complet : le cercle limite de Beltrami n’est qu’un cas particulier de la conique absolue de Cayley, dans le cas où la géométrie est hyperbolique.
C’est à sa présentation (très rapide) qu’est consacrée cette page, en vue de faire des figures plus complexes sur la pseudosphère par conjugaison avec ce modèle.
Le plan hyperbolique (on dira KB dans la suite pour parler de ce modèle) est l’intérieur d’un cercle, que nous appellerons horizon. Comme dans le modèle DP (disque de Poincaré), les points du cercle sont les points à l’infini, nous dirons, conformément à la terminologie usuelle, idéaux (ce qui n’est pas la même terminologie que le mémoire de Beltrami). Les points du modèle sont les points à l’intérieur du cercle, et les droites sont les cordes du cercle. Voici pour l’incidence. Reste l’essentiel, la partie métrique, soit la donnée d’une orthogonalité, des symétries orthogonales . Parce qu’il voulait inclure les trois types de géométrie (qu’il sera le premier à appeler hyperbolique, parabolique, elliptique) dans un plongement projectif, la lecture que fait Klein du disque limite de Beltrami est fondamentalement projective. On commence donc par quelques rappels, très ciblés, et contextualisés aux cercles (au lieu de coniques générales) sur ce thème.
Rappel de quelques définitions de géométrie projective
Division harmonique
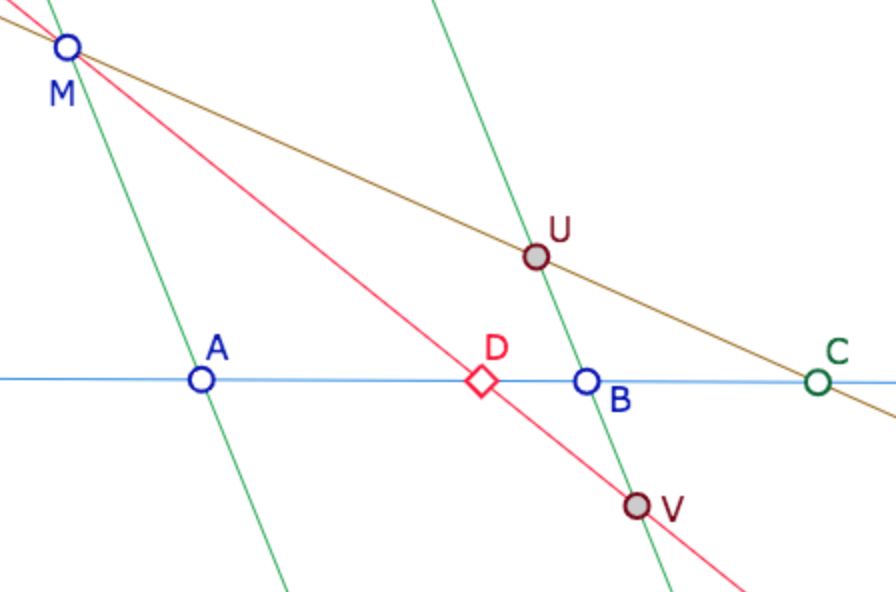
\(A, B\) étant donnés et \(C\) un point de la droite \((AB)\). À partir de tout point \(M\) n’appartenant pas à \((AB)\), on construit l’intersection \(U\) de \((MC)\) et de la parallèle à \((AM)\) passant par \(B\) . Soit alors \(V\) le symétrique de \(U\) par rapport à \(B\) . La droite ( \((MV)\) coupe \((AB)\) en un point \(D\) , indépendant du point \(M\) , et qui vérifie
\(\displaystyle \frac{\overline{CA}}{\overline{CA}} = – \frac{\overline{DA}}{\overline{DB}}\)
\(D\) est le conjugué harmonique de \(C\) par rapport à \((A, B)\) .
Pour des raisons immédiates de symétrie dans le birapport, on dit que les couples (A, B) et (C, D) sont en division harmonique.
Pôle d’une droite
Etant donné un cercle \(\Gamma\) et une droite \(d=(UV)\), la perpendiculaire à \(d\) issue du centre du cercle coupe le cercle en \(A\) et \(B\) et \(d\) en \(H\). On appelle pôle de \(d\) par rapport à \( \Gamma \) le conjugué harmonique \(P\) de \(H\) par rapport à \(A\) et \(B \).
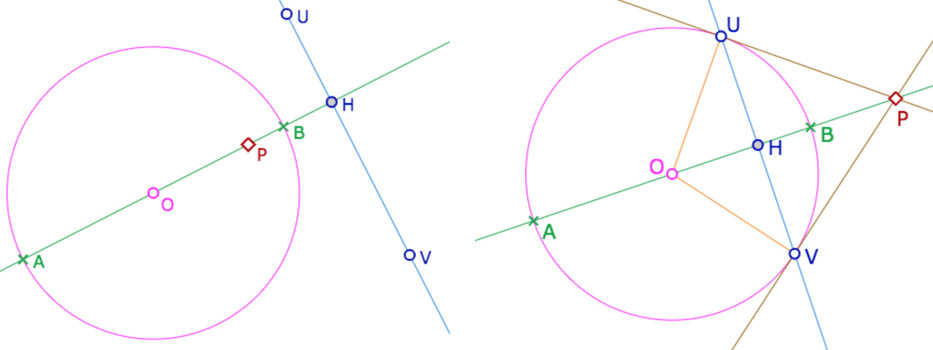
Pour ce qui va nous intéresser dans KB, on sera dans le cas de la seconde illustration où la droite coupe le cercle en deux points \(U\) et \(V\). Alors le pôle de la droite est aussi l’intersection des tangentes (relations métriques dans le triangle rectangle).

Polaire d’un point
C’est la définition réciproque : à partir de \(P\) on construit la droite \((OP)\) et \(H\) conjugué harmonique de \(P\) par rapport à \(A\) et \(B\). La polaire est la perpendiculaire à \((OP)\) en \(H\).
Homologie harmonique
Étant donnés une droite \(d\) et un point \(P\), l’application qui, à un point \(M\) du plan associe le point \(M’\), conjugué harmonique de \(M\) et \(I\) où \(I\) est l’intersection de \((PM)\) et de \(d\) s’appelle l’homologie harmonique d’axe \(d\) et de pôle \(P\).

Elle est involutive et conserve le contact. Le pôle \(P\) et les points de l’axe \(d\) sont invariants; les droites passant par le pôle sont globalement invariantes. Elle conserve la conjugaison harmonique et la polarité.
La propriété importante de l’homologie pour ce qui nous occupe est la suivante : Soit \(A\) un point. Une conique est globalement invariante par l’homologie de pôle \(A\) et d’axe la polaire de \(A\) par rapport à cette conique. Cette propriété, appliquée au cercle, va faire des homologies harmoniques – d’axe une droite coupant le cercle et de centre le pôle de son axe – les symétries orthogonales du modèle KB. Elle est aussi présente dans la prochaine construction.
Axe d’une symétrie orthogonale – d’une homologie harmonique – dans le modèle KB
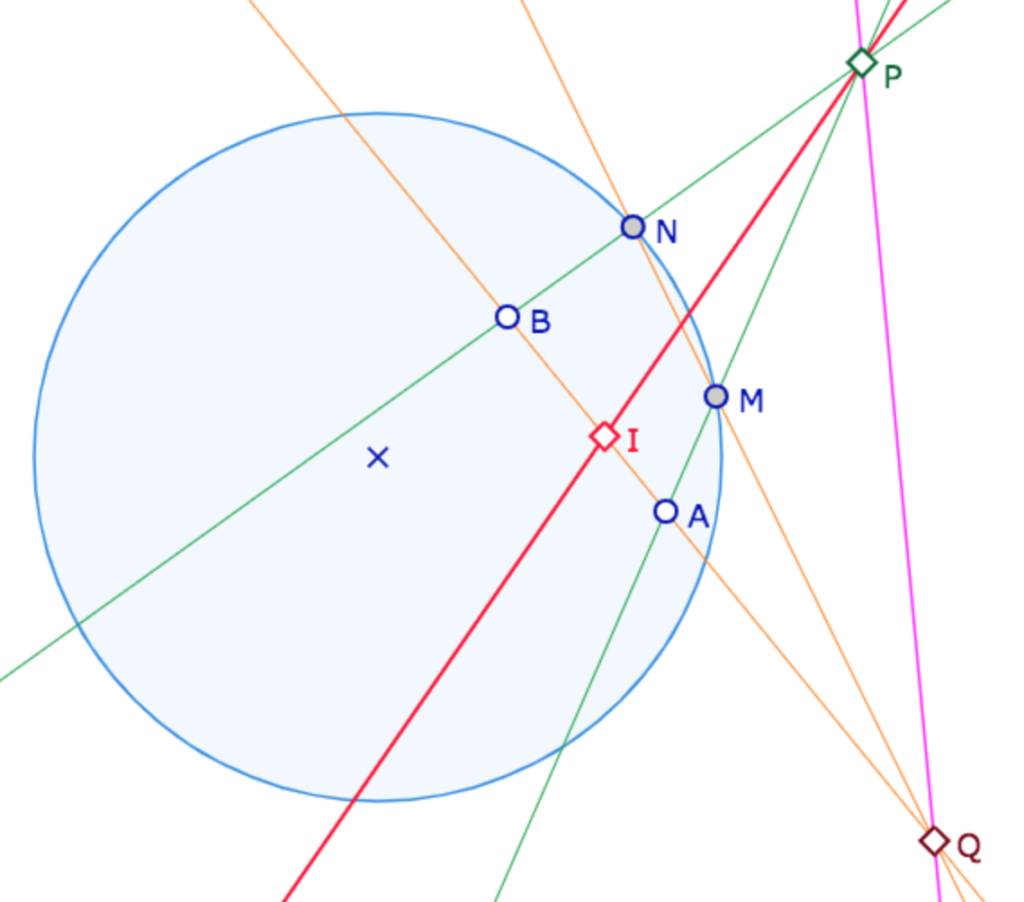
Étant donnés deux points \(A\) et \(B\) à l’intérieur du cercle horizon, il existe une infinité d’homologies harmoniques échangeant les deux points d’axe passant par \(P\) le pôle de \((AB)\), mais deux seulement laissent le cercle horizon invariant, dont une a son centre à l’extérieur du cercle : c’est celle que l’on veut construire.
Soient donc \(A\) et \(B\) à l’intérieur du cercle horizon, on construit \(P\) son pôle par rapport au cercle, puis \(M\) et \(N\) les intersections de \((PA)\) et \((PB)\) avec le cercle et \(Q\) l’intersection de \((MN)\) et \((AB)\). Alors l’axe de la KB-symétrie orthogonale est la polaire de \(Q\) par rapport au cercle (en rouge ci-contre). Ce sera aussi la KB-médiatrice de \(A\) et \(B\).
L’autre homologie harmonique échangeant \(A\) et \(B\) et laissant le cercle horizon invariant est celle d’axe \((PQ)\) et de pôle l’intersection \(I\)de \((AB)\) et de la polaire de \(Q\). Cela ne peut pas être une symétrie orthogonale pour KB, mais \(I\) est le KB-milieu de \(A\) et \(B\), et donc le centre de symétrie des deux points.
L’orthogonalité dans KB

Perpendiculaire
La perpendiculaire à la droite ou au segment \([AB]\) issue de \(M\) est la trace dans le cercle horizon de la droite passant par \(M\) et le pôle \(Pab\) de \((AB)\) par rapport au cercle. Ci-contre on illustre aussi la symétrie de l’orthogonalité (conséquence de l’homologie harmonique) : le pôle de cette perpendiculaire est sur la droite euclidienne \((AB)\) et donc la droite \((AB)\) est bien elle aussi perpendiculaire à sa perpendiculaire : la relation d’orthogonalité est symétrique.
Perpendiculaire commune
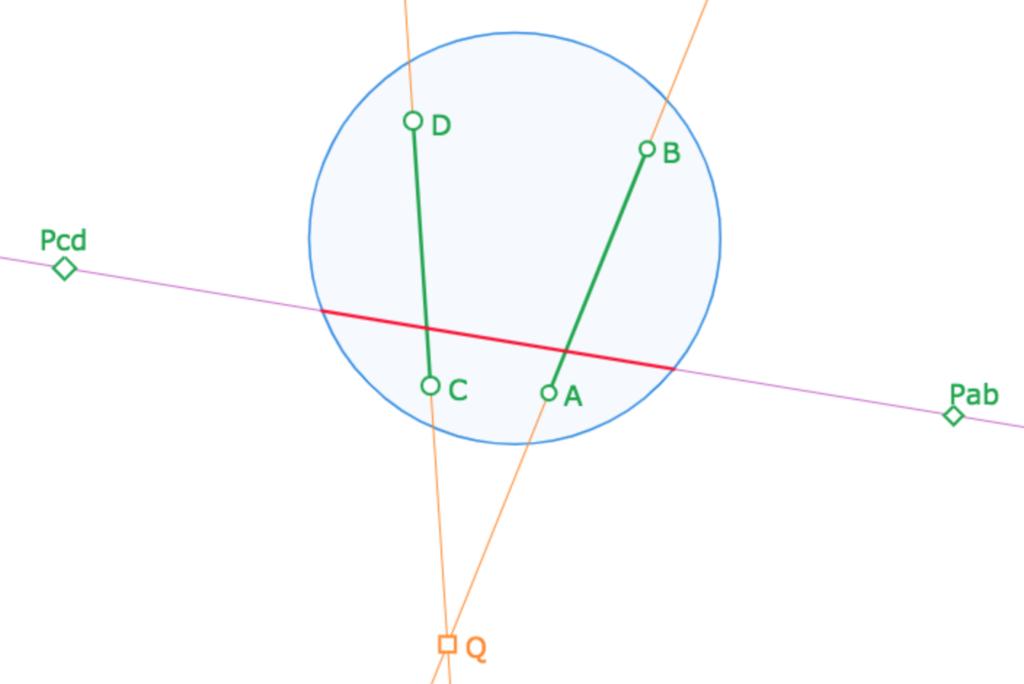
La perpendiculaire commune à deux droites ou segments \((AB)\) et \((CD)\) est aussi bien la trace sur l’horizon de leur droite des pôles que la polaire de leur intersection euclidienne.
Quand les droites hyperboliques \((AB)\) et \((CD)\) sont sécantes ou parallèles, elles n’ont pas de perpendiculaires communes et la droite euclidienne \((P_{ab}P_{cd})\) ne coupe pas – respectivement est tangente – au cercle horizon.
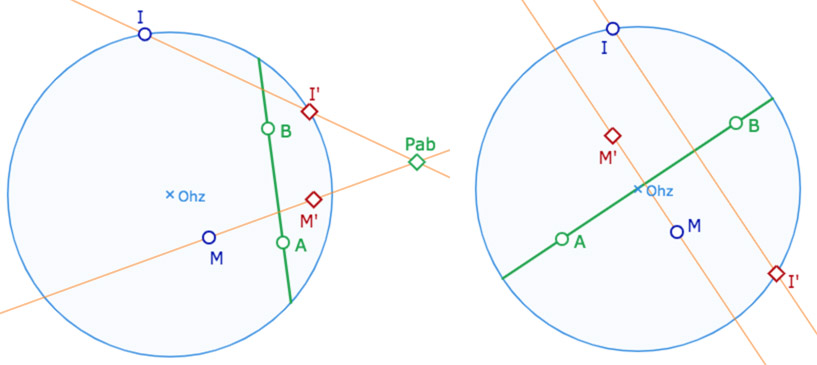
Symétrie orthogonale
Ci-dessous \(I’=s_{AB}(I)\) et \(M’=s_{AB}(M)\). Dans cette figure, on peut vérifier que
• l’image d’un demi-plan est un demi-plan (la symétrie orthogonale hyperbolique est encore un pliage, comme dans le cas euclidien).
• l’image du point idéal \(I\) est le point idéal \(I’\).
• les seules droites globalement invariantes sont les perpendiculaires à l’axe (qui donc passent par le pôle \(P_{ab}\) de la droite \((AB)\).
• Quand l’axe \((AB)\) passe par le centre du cercle, son pôle est à l’infini et la KB-symétrie orthogonale est alors la symétrie orthogonale euclidienne usuelle (car une homologie harmonique dont le pôle est à l’infini est une symétrie orthogonale)
Les cercles de KB
KB-distance

Historiquement, c’est à Cayley que l’on doit (1859) l’introduction de la distance suivante, construite sur le bi-rapport, à l’intérieur d’une conique qui fait de l’intérieur de cette conique, une géométrie hyberbolique. Ce résultat a réellement été achevé en 1871 par Klein, en particulier avec le modèle que l’on étudie ici :
\(d(A,B) = \displaystyle \frac{1}{2} \left\vert ln \left(\frac{AU}{AV} : \frac{BU}{BV}\right) \right \vert\)C’est celle que l’on utilise pour le disque de KB.
KB-cercle
Comme toujours, il y a deux approches du cercle de centre \(O\) passant par \(A\).
• L’approche métrique, celle de la ligne de niveau \(d_{KB}(O,M)=d_{KB}(O,A)\)
• L’approche géométrique, le lieu des symétriques \(M\) de \(A\) dans toutes les symétries passant par \(O\).
Par les deux approches, il est immédiat qu’un KB-cercle de centre le centre \(O_{hz}\) du cercle horizon passant par un point \(A\) est le cercle euclidien. En effet les KB-symétries d’axe passant par \(O_{hz}\) sont les symétries euclidiennes. De même \(O_{hz}U=O_{hz}V\) sur la droite \((O_{hz}A)\) comme sur la droite \((O_{hz}M)\) et donc \(d_{KB}(O_{hz},M)=O_{hz}M)\) et \(d_{KB}(O_{hz},A)=O_{hz}A\). Autrement dit la ligne de niveau \(d_{KB}(O_{hz},M)=d_{KB}(O_{hz},A)\) s’écrit, avec la distance euclidienne, \(O_{hz}M=O_{hz}A\) , le KB-cercle de centre \(O_{hz}\) est le cercle euclidien.
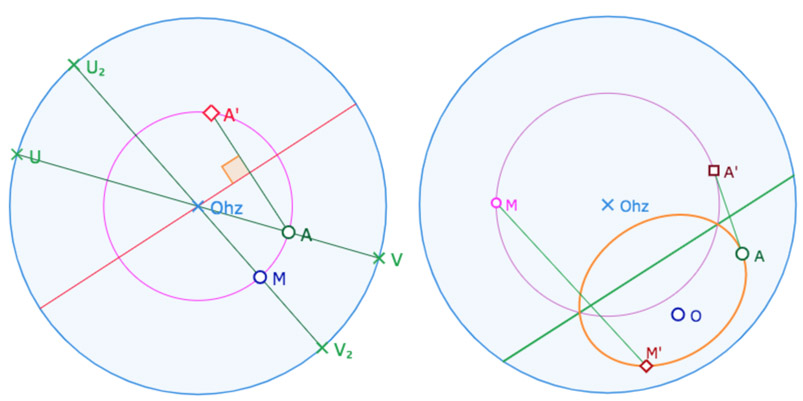
Alors, le cercle de centre \(O\) passant par \(A\) peut se construire par conjugaison avec un centre de centre \(O_{hz}\). pour cela on construit une macro Médiatrice avec \(O_{hz}\). L’image de \(A\) par la symétrie associée à cette médiatrice est notée ci-dessus \(A’\). L’image du cercle cherché est le cercle de centre \(O_{hz}\) passant par \(A’\). Un point \(M\) de ce cercle a pour image – mais aussi provient – de son symétrique \(M’\). Le cercle cherché est le lieu de \(M’\) quand \(M\) décrit le cercle euclidien. C’est une ellipse euclidienne. En pratique, pour faire la macro KB-cercle, on n’utilise pas ce lieu. En étudiant un peu plus cette figure on construit l’ellipse avec un nombre d’objets intermédiaires optimisé.
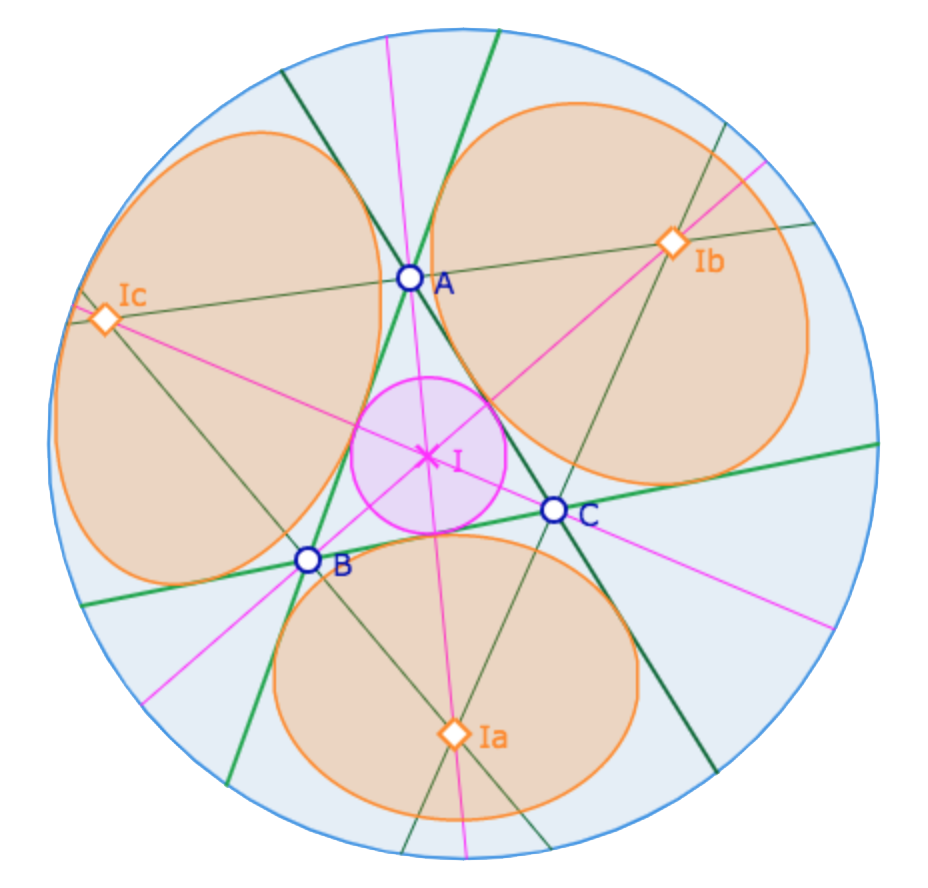
KB-bissectrices
On reprend la technique utilisée pour les bissectrices dans DP : on prolonge les segments d’un triangle en demi-droites pour utiliser un triangle avec deux points idéaux. Alors la bissectrice d’un angle du triangle est la hauteur du triangle idéal associé car celui-ci est isocèle. On peut alors construire facilement les configurations usuelles comme les cercles exinscrits ci-contre.
Pour les trilatères, les constructions sont plus simples à réaliser que dans DP car le modèle étant intimement projectif, on peut travailler directement dans son plongement projectif au plan tout entier avec les mêmes outils.
Par exemple, un faisceau de droites est toujours « à centre » dans le plongement projectif.
Ci-dessous, quelques illustrations autour du point de Gergonne d’un KB-trilatère.
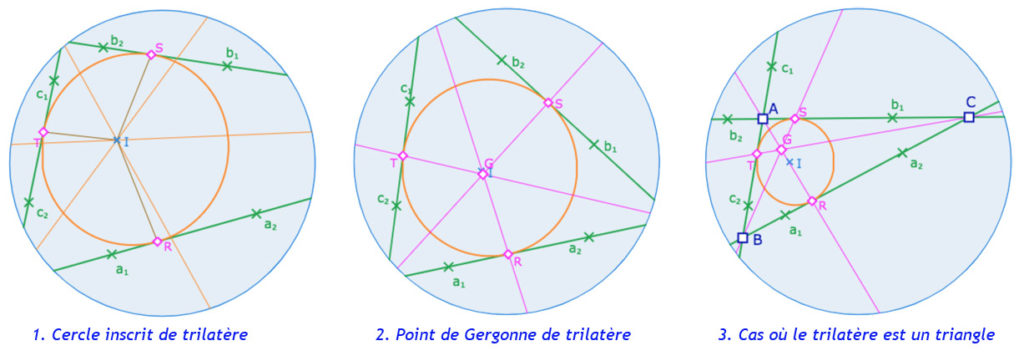
Manipulation de la figure
Dans cette figure on agit sur les droites \(a, b\) et \(c\), par leurs poignées indicées 1 et 2.

Les horicycles et les équidistantes de KB
Les constructions sont élémentaires, à partir de leurs définitions. Un KB-horicycle est représenté par une ellipse tangente au cercle horizon en son centre. Une KB-équidistante est représentée par une partie de l’ellipse passant par M, bi-tangente au cercle horizon en les points idéaux de l’axe de l’équidistante. C’est l’arc de la partie de l’ellipse – délimité par l’axe – contenant le point M.

Illustration sur les médiatrices d’un triangle selon que le faisceau des médiatrices soit, à centre, sans support, ou à axe.
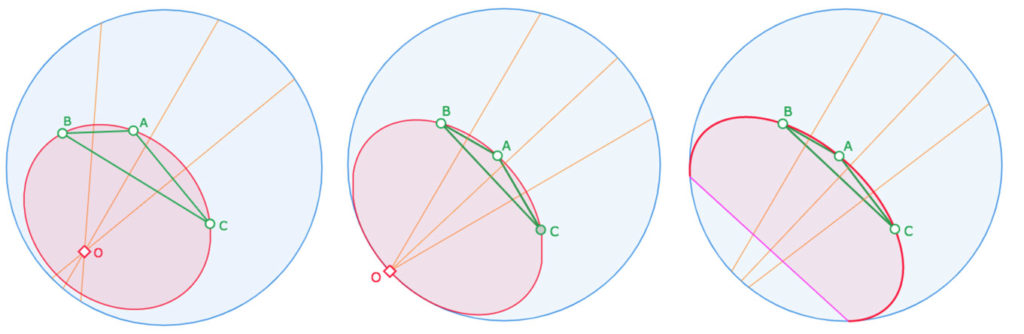
On observera que le cas des médiatrices sur un horicycle, le point \(C\) est construit, sinon l’horicycle n’aurait été que « approché ».
Cycles exinscrits d’un triangle
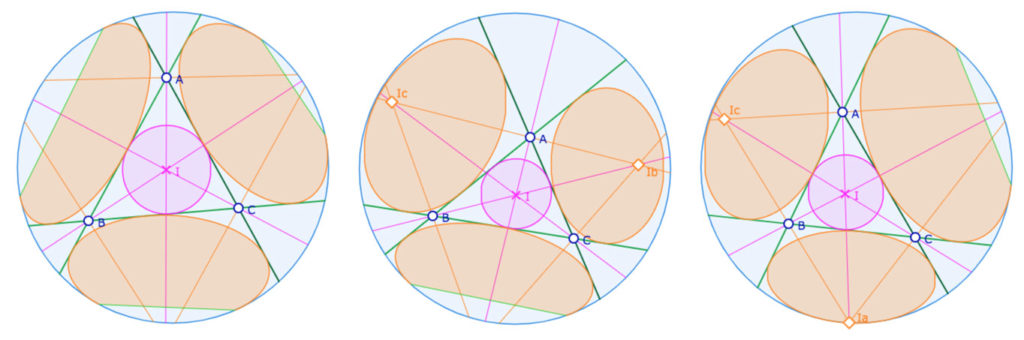
à gauche, trois équidistantes, au centre une équidistante et deux cercles,
à droite, un cercle une équidistante et un horicycle (approché)
Manipuler la figure
Dans cette figure on agit sur les points \(A, B\) et \(C\).
Horicycles exinscrits
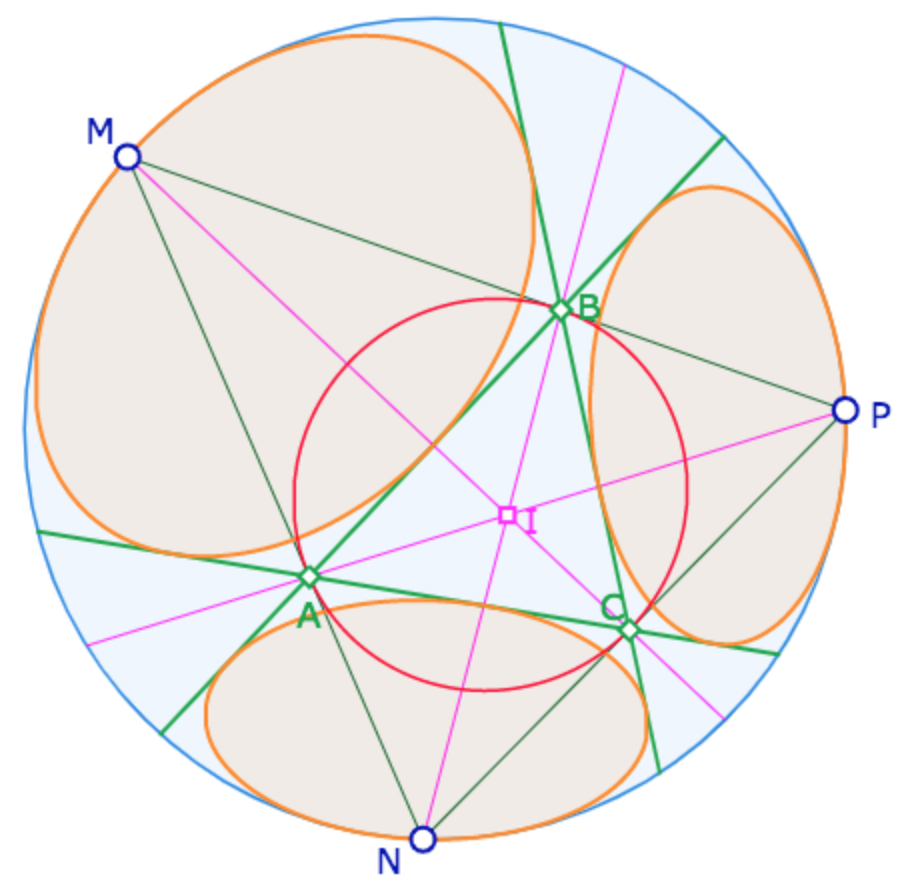
Un résultat hyperbolique classique sur les horicycles exinscrits
Comme il n’est pas possible de réaliser, « à la souris », un triangle ayant ses trois cycles exinscrits qui soient trois horicyles, on prend le problème à l’envers : on se donne trois points idéaux \(M, N, P\) et on construit, le cercle inscrit à \(MNP\), de centre \(I\), qui est aussi le cercle circonscrit à \(ABC\), le triangle podaire de \(MNP\) puisque les bissectrices de \(MNP\) sont aussi ses hauteurs : \(MNP\) est équilatéral d’angle au sommet nul (et de côté « infini »).
Alors \(ABC\) est équilatéral de côté fixe égal à \(2 ln(\varphi)\), où \(\varphi\) est les nombre d’or. Par ailleurs le rayon \(IC\) du cercle circonscrit à \(ABC\) vérifie \(IC = \displaystyle \frac{ln \,3}{2}\).
Ces résultats sont montrés dans ce petit article utilisant les calculs de trigonométrie hyperbolique du mémoire de Bolyaï.
Manipuler la figure
En déplaçant \(M, N\) ou \(P\), les calculs des distances affichées sont recalculées … et on illustre qu’elles sont constantes
Compléments
Plusieurs articles de blog sont consacrés au modèle de Klein-Beltrami, en particulier pour son utilisation avec les différentes surfaces pseudosphériques
Jouer avec les pavages de KB : contient des macros qui permettent de refaire rapidement les pavages proposés.
Troncatures de P54, P64 et P38 dans KB : continuation du précédent. Partiellement réinvestit ensuite sur la PSH.
Plongement projectif
Deux articles sont consacrés au plongement projectif de KB dans ce que l’on a appelé KH (pour Klein Hyperbolique) en lien avec le plan elliptique KE (pour Klein Elliptique).
Attention : le plongement projectif de KB est projectif, pas hyperbolique au sens que l’on a dégagé ici.
L’intérêt de ces articles est surtout son point de vue très différent de l’approche classique des GNE, par les formes quadratiques.