Géométrie intrinsèque des surfaces
En dégageant le concept de géométrie différentielle (1828), Gauss ouvrait un champ d’investigation aussi nouveau que prometteur. Sa démarche a été de considérer les surfaces comme étant intrinsèquement de dimension 2. Après y avoir défini des coordonnées curvilignes et la forme quadratique associée (forme fondamentale), Gauss dégage les notions propres à la surface (la courbure géodésique et les lignes associées par exemple) de celles qui sont liées à son plongement dans un espace euclidien environnant (courbure intégrale, seconde forme fondamentale) et fait le lien entre elles – le fameux theorema egregium. Ceci étant fait, il s’intéresse ensuite à la notion d’isométrie locale ce qui aboutit à la notion de géométrie intrinsèque des surfaces.
En 1863, Beltrami est nommé professeur de géodésie à l’université de Pise. Il s’intéresse à la cartographie, la représentation des surfaces sur un plan avec cette problématique générale et récurrente : « dans quelle mesure au plus court chemin sur la surface peut-on faire correspondre le plus court chemin sur le plan – le segment ? ». D’ où cette recherche fondamentale de la linéarisation des géodésiques.
Beltrami connaît bien le traité de Gauss, il l’a même traduit en italien. Par ailleurs, comme spécialiste de géodésie, il connaît bien entendu aussi un résultat plus ancien et qu’il imagine prometteur de Lagrange (1779) sur la construction des cartes de la planisphère : la projection depuis le centre de la sphère sur un plan fait correspondre, d’une part aux géodésiques (les grands cercles) les droites, et réciproquement, seule aux géodésiques correspondent les droites : pour la sphère, la question a donc été entièrement résolue, et de manière simple et élégante par Lagrange. Beltrami pense naturellement qu’avec les outils contemporains de la géométrie des surfaces, ce résultat sur la sphère devrait facilement trouver une généralisation. Et l’aventure de Beltrami commence par un résultat négatif qui le déçoit dans un premier temps :
« … les seules surfaces susceptibles d’être représentées sur un plan, en sorte qu’à chaque point de l’une corresponde un point de l’autre et qu’à chaque ligne géodésique corresponde une ligne droite, sont celles dont la courbure est partout constante (positive, négative ou nulle). »
« Risoluzionne del problema : Riportare i punti una superficie sopra un piano in modo che le geodetiche vengano rappresentate da linee rette » (1865)
Mais Beltrami persiste, et s’intéresse donc aux surfaces à courbure constante négative. Dans son projet, initialement, il n’y a pas de recherche de représentation de la géométrie de Lobatchevsky, il ne le lira qu’en 1866, juste l’interrogation naturelle pour une problématique fondamentale de géodésique …
Pour arriver à son résultat, dans son article de 1865, Beltrami avait déjà mis en évidence une paramétrisation totalement adaptée à la linéarisation des géodésiques des surfaces à courbure constante négative, plus précisément, ses coordonnées curvilignes (on dira « coordonnées beltramiennes » conformément à l’usage) sont telles que toute équation linéaire représente une géodésique et réciproquement toute géodésique est représentée par une équation linéaire des coordonnées beltramiennes.
La pseudosphère
Il poursuit son travail en approfondissant l’étude du cas particulier de surfaces à courbure constante négative. Il n’est pas le premier. Cette étude avait été inaugurée par Gauss lui-même qui avait déjà mentionné la pseudosphère sous le nom de « Gegenstück der Kugel » (homologue à la sphère) et montré – entre autres – que l’aire l’un triangle géodésique \(ABC\) sur une surface de courbure constante \(\displaystyle \frac{-1}{R^2}\) est \(R^2(\pi-\widehat{A}-\widehat{B}-\widehat{C})\), avec la mesure des angles en radians. Elle avait surtout été poursuivie par Minding, en 1839 lors d’une étude sur le développement d’une surface sur une autre. Lui aussi avait été amené à décrire la pseudosphère comme cas particulier élémentaire de surface à courbure constante négative : dans l’intégration d’une équation aux dérivées partielles, il choisit un des coefficients nul ce qui élimine un terme rectangle largement plus délicat à intégrer dans le cas général. Ce sont les surfaces peudosphériques hyperbolique et elliptique que l’on aborde dans le menu PSH.
La question de l’enroulement
Minding a montré que pour être « développables l’une sur l’autre », les surfaces doivent être à courbure constante et de même courbure. Ce résultat sera essentiel quand Beltrami aura à expliquer la possibilité de l’enroulement de la pseudosphère sur elle-même. On parle depuis de « revêtement » de la pseudosphère. Selon les historiens des mathématiques, les résultats de Minding, en particulier les nombreux développements trigonométriques de ses articles de 1839 et 1840 contenaient assez d’éléments pour faire le lien avec les relations trigonométriques de « la théorie des parallèles » de Lobatchevsky, mais encore fallait-il connaître ces travaux, peu répandus alors à cette époque. Or ceux-ci ont été traduits, en particulier en français par Jules Hoüel, en 1866, dans la version de 1840, écrite en allemand. Beltrami en a pris connaissance et a commencé, sur la base de ses propres développements – en particulier son système de coordonnées curvilignes – à se pencher sur la correspondance entre la géométrie naturelle des surfaces à courbure constante négative et la géométrie plane de Lobatchevsky.
Le disque limite de Beltrami
Dans son « Essai d’intreprétation de la géométrie non euclidienne » de 1868, Beltrami reprend son système de coordonnées curvilignes \((u, v)\) d’une surface à courbure constante négative et calcule l’angle entre les deux lignes géodésiques coordonnées u= constante et v = constante. Il rencontre alors le terme \((a^2-u^2-v^2)\) où \(a\) est une constante. Ses calculs n’ont donc de sens que pour \((u, v)\) – considérées maintenant comme coordonnées cartésiennes dans un plan euclidien – à l’intérieur d’un cercle de rayon \(a\) qu’il appelle cercle limite, et dont il montre en détail que les points correspondent aux points à l’infini de la surface qu’il étudie.
Pour Beltrami, son disque limite n’est qu’un outil intermédiaire pour son étude des géodésiques. Quelques mois après la publication de son essai, Klein compris immédiatement que le disque limite de Beltrami était en fait un modèle du plan hyperbolique, et même un modèle du plan hyperbolique entier, ce qui n’est pas le cas de la pseudosphère.
La mise en évidence de la géométrie hyperbolique
Dans la troisième partie de son essai, Beltrami entame l’étude des angles entre les géodésiques en fonction des angles des cordes correspondantes dans le disque limite, et il fait ce que l’on peut appeler la première « vraie » figure hyperbolique, même si lui-même ne la percevait pas comme cela – dans le futur modèle de Kein-Beltrami, figure qu’il commente ainsi :
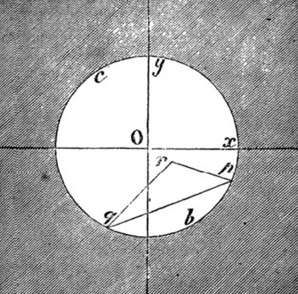
Par un point (réel) quelconque de la surface, on peut toujours mener deux lignes géodésiques (réelles), parallèles à une même ligne géodésique qui ne passe pas par ce point, et ces deux lignes géodésiques font entre elles un angle qui diffère à la fois de 0 et de 180 degrés.
Ce résultat s’accorde, sauf la différence des termes employés, avec ce qui forme la base de la géométrie non euclidienne.
« Essai d’interprétation de la géométrie non euclidienne » – Beltrami – 1868
On reviendra, dans l’item proposant une lecture illustrée de son « essai d’interprétation », sur l’ambiguité du terme « point réel » chez Beltrami.
Une construction physique de la pseudosphère
Parce qu’il n’était pas intéressé par l’axiomatique, la problématique d’un modèle d’une géométrie non euclidienne ne concernait pas Beltrami. Aussi, quand il a (très rapidement d’ailleurs) pris conscience que la géométrie des surfaces à courbure constante était – au moins localement – régie par la géométrie des plans de Lobatchevsky fut-il essentiellement concerné par la mise en place d’une correspondance bijective entre le plan de Lobatchevsky (au tout au moins une partie) et certaines surfaces à courbure constante négative.
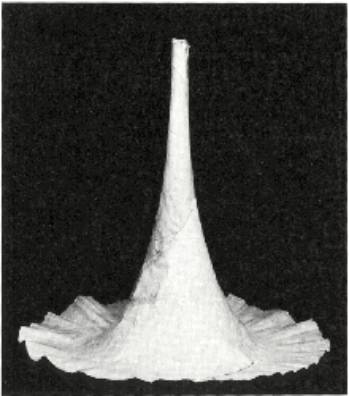
En partie pour répondre aux critiques de l’époque sur l’existence même de surfaces pseudosphériques – mais aussi pour vérifier les résultats de son essai, et expérimenter, Beltrami a plusieurs fois construit physiquement (des approximations de) ces surfaces, de 1869 à 1872.
« Ce matin, avec l’aide d’un de mes élèves, qui est bon dessinateur, j’ai découpé un modèle en carton qui m’est assez bien réussi, et qui me servira pour un nouvel essai de construction d’une surface pseudosphérique. Vous parlez de proposition empirique que l’on pourrait trouver par ce moyen, et vous avez raison, car il s’agit de surfaces dont on ne possède pas les équations générales. Voici précisément une proposition empirique que j’ai commencé à soupçonner : Une surface pseudosphérique peut toujours être pliée de manière qu’une quelconque de ses lignes géodésiques devienne une ligne droite. »
Lettre à Jules Hoüel, du 25 mars 1869 – La découverte de la géométrie non euclidienne sur la pseudosphère – lettres d’Eugenio Beltrami à Jules Hoüel (1868-1881)
Présentation des items de ce menu PS
Dans le premier item, on présente la construction pratique des segments et des droites sur la pseudosphère. On aborde rapidement la question de l’enroulement des objets sur les différentes feuilles. On présente une figure permettant de placer des points sur les deux feuilles autour de la feuille principale.
Les deux items suivants abordent les premières propriétés des triangles sur la pseudosphère, tout d’abord sur les milieux, et second sur l’orthogonalité. Ces résultats sont produits dans le cadre de la géométrie intrinsèque des surfaces : les calculs sont fait sur la pseudosphère. C’est encore le cas dans l’item suivant sur les cercles. On poursuit l’exploration des cycles dans l’item suivant, consacré aux équidistantes et aux horicycles. Pour cela, on utilise les calculs sur l’orthogonalité pour se permettre, avec les outils développés, des constructions plus géométriques sur la pseudosphère pour ces deux cycles biens particuliers. La pseudosphère étant un modèle local, on ne peut explorer que des traces de ces objets sur la pseudoshère. Jusqu’ici, tout est entièrement fait sur la pseudosphère. Et ce dernier item est l’occasion de présenter (un peu rapidement) la façon de travailler pour réaliser ces figures.
Ensuite, pour réaliser des figures plus complexes, on a choisi de travailler par conjugaison avec le « Disque Limite » (DL) de Beltrami qu’on appelle depuis le modèle de Klein-Beltrami. Pour cela un item d’interlude présente les objets de base – dont l’orthogonalité et les cycles – de ce modèle.
Puis deux items sont consacrés à la conjugaison : une page de présentation et d’application immédiate sur l’exemple des cycles circonscrits à un triangle, puis une page de réalisation plus originales comme le « rêve de Coxeter » qui consiste à enrouler une courbe – en fait une équidistante – à l’infini sur « la corne de la pseudosphère » pour reprendre les mots de Coxeter lui-même.
Un dernier item reprend quelques points du mémoire de Beltrami en les illustrant de figures dynamiques.