Somme des angles d’un triangle intérieur à l’ellipse et conséquences
Dans sa définition des angles, Hilbert précise qu’en dehors des points très spécifiques de l’ellipse, la définition des angles est celle usuelle. Dans le cas de trois points à l’intérieur de l’ellipse, la somme des angles est constante et égale à 180°. La propriété n’est bien entendu pas liée à ce que les points soient intérieurs à l’ellipse, mais bien au fait que les trois cercles définissant les côtés des triangles soient concourants en \(F\). La H-longueur des segments est la longueur euclidienne des objets utilisés. On peut donc s’intéresser à la longueur des côtés d’un triangle ayant ses trois angles égaux. Ci-dessous, à gauche, on se donne deux sommets \(B\) et \(C\) et on construit \(A\) tel que les angles en \(B\) et \(C\) soient de 60°. On mesure les longueurs des côtés. On voit alors que le triangle n’est pas équilatéral (même longueur).
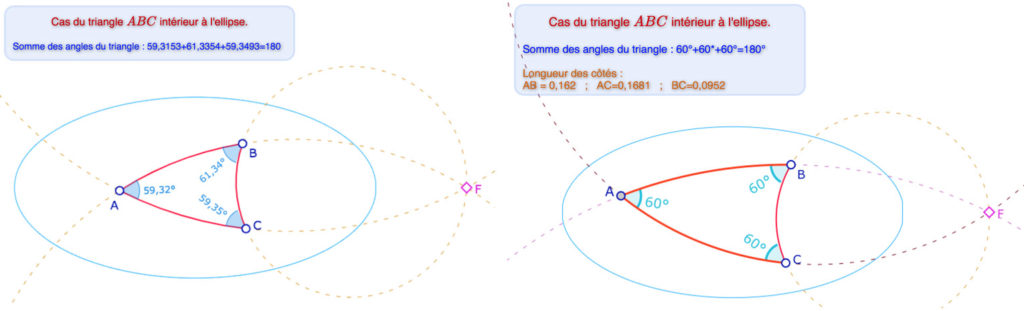
On peut manipuler ces deux figures dans d’autres onglets (se mettre en mode consultation, aucun outil sélectionné) en conservant, bien entendu, les points à l’intérieur de l’ellipse:
• H-triangle dans l’ellipse comme illustré à gauche et
• H-triangle intérieur à l’ellipse dont les trois angles mesurent 60° (illustration de droite).
Eléments de preuve pour « somme des angles égale à deux droits »
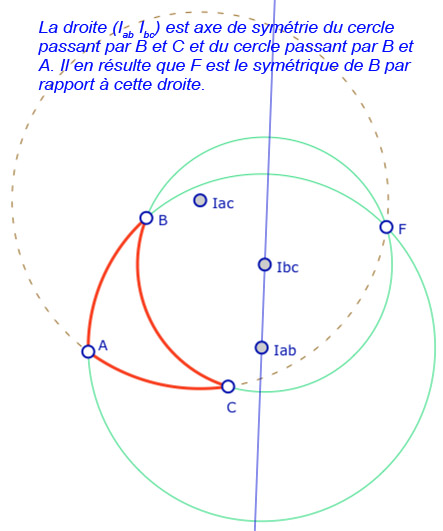
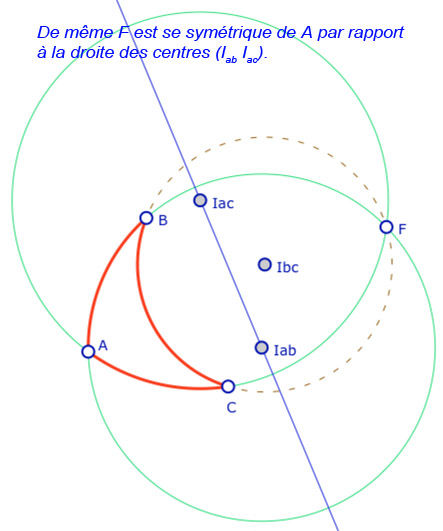
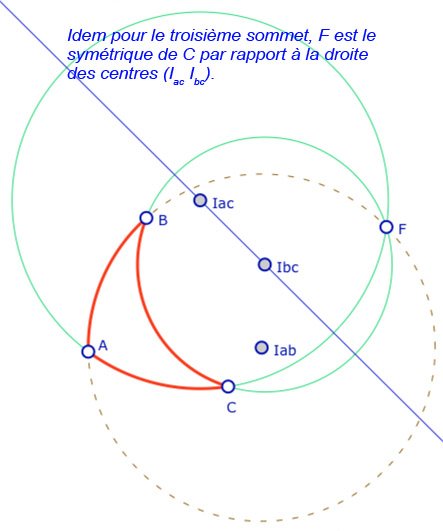
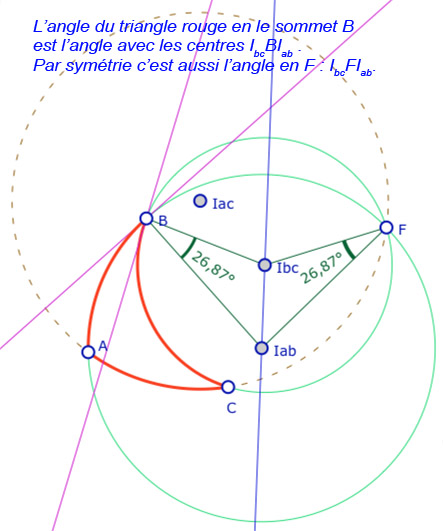
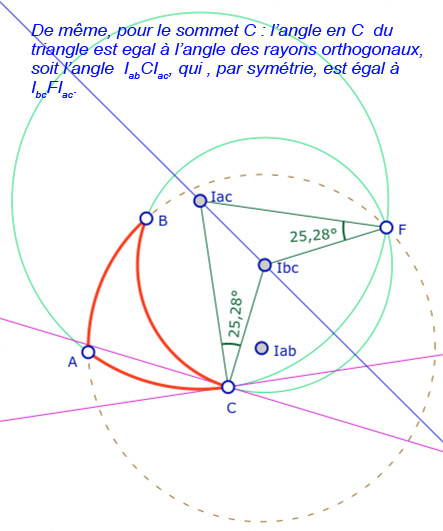
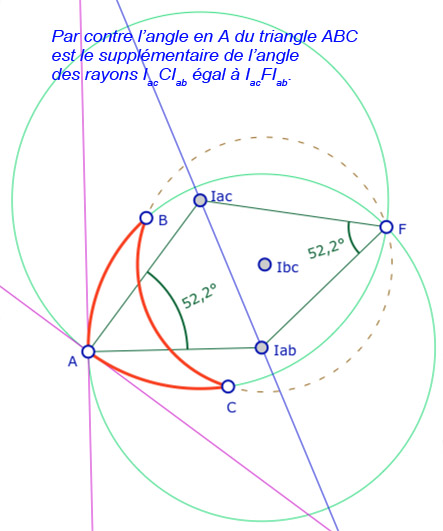
On travaille sur une figure générique (hors du rapport à l’intérieur de l’ellipse), en conservant seulement que les trois points \(A, B, C\) sont du même côté (à gauche) du point \(F\). Commençons par observer les égalités d’angles dégagées dans cette galerie (6 illustrations) :
Si, dans ces illustrations, on a l’égalité \(\angle I_{ac}FI_{bc} + \angle I_{bc}FI_{ab} = \angle I_{ac}FI_{ab}\), dans le cas général, selon quel est le segment \([I_{xy}F]\) entre les deux autres, il est clair que c’est le plus grand des trois angles en \(F\) qui est égal à la somme des deux autres … et donc selon lequel des centres des trois cercles est d’ordonnées entre les deux autres.
Or c’est aussi pour le plus grand de ces trois angles (entre \(\angle I_{bc}BI_{ab} , \angle I_{ac}AI_{ab} , \angle I_{ac}CI_{bc}\) ) qu’il faut prendre le supplémentaire pour obtenir l’angle de \(ABC\) en le sommet considéré.
La somme (des mesures) des angles est alors : \(180 + \angle I_{bc}BI_{ab} + \angle I_{ac}AI_{ab} + \angle I_{ac}CI_{bc} – 2 \times max(\angle I_{bc}BI_{ab} , \angle I_{ac}AI_{ab} , \angle I_{ac}CI_{bc})\), soit d’après ce qui précède : 180°.
Une conséquence immédiate mais significative
On se donne trois points \(A, B, C\) et tel que l’angle en \(B\) soit droit. Puis on construit \(D\) tel que \(ABCD\) ait ses trois angles en \(A\) et \(C\) droits. On a vu qu’alors l’angle en \(D\) est droit. On a donc un quadrangle rectangle : un quadrilatère dont les quatre angles sont droits.
Sur l’illustration de gauche, on fait apparaitre plusieurs résultats. Tout d’abord, une vérification « logicielle » que l’angle en \(D\) est droit (c’est le logiciel qui construit la marque « du droit »). Ensuite on voit les alignements des centres euclidiens des cercles supports. \(IorthBC\) est le centre du cercle passant par \(A\) et \(F\), orthogonal à \((BC)\). De même \(IorthAB\) est le centre du cercle orthogonal à \((AB)\)passant par \(A\) et \(F\).
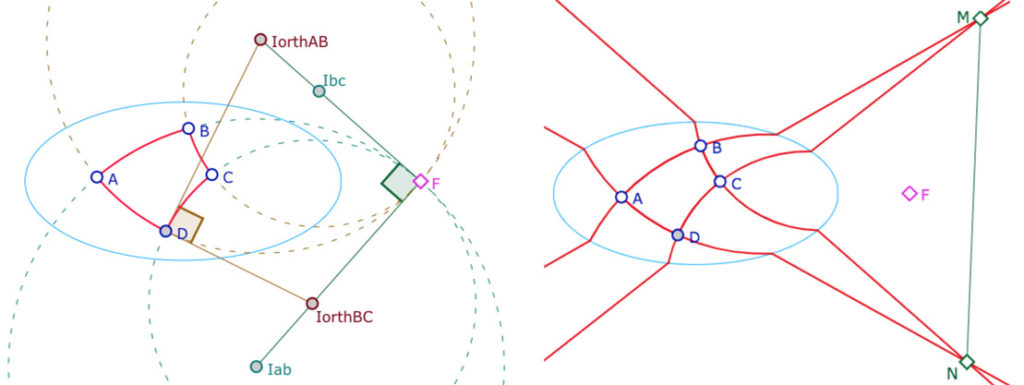
Sur l’illustration de droite, non seulement on illustre que les H-droites support des côtés opposés d’un rectangle ne sont pas parallèles. Mais surtout, il en résulte que l’on construit ainsi deux points \(M\) et \(N\) desquels on peut mener deux perpendiculaires, non seulement à une droite, mais même à deux droites non parallèles : de \(M\) on mène deux perpendiculaires à \((NB)\) mais aussi à \((NA)\) … et ce sont les mêmes. De même en inversant les rôles de \(M\) et \(N\).
Il en résulte par exemple que le triangle \(MAN\) est rectangle en \(A\) mais possède une autre hauteur issue de \(M\) et une autre issue de \(N\). On verra dans les pages sur l’orthogonalité comment modifier la figure pour que \(C\) soit un second orthocentre de \(MAN\).
Manipulation de la figure associé
Autres propriétés de la géométrie à l’intérieur de l’ellipse
Dans ce paragraphe, nous allons voir quelques propriétés immédiates d’un triangle intérieur à l’ellipse. Ce sont essentiellement des conséquences de l’inversion.
Hauteurs et intersection des médianes d’un H-triangle intérieur à l’ellipse
Les hauteurs sont les traces des cercles orthogonaux aux cercles supports des côtés du triangle. Les milieux des côtés du H-triangle sont les milieux usuels des arcs de cercle, ce qui permet de construire les médianes. Comme la figure est non liée à l’ellipse, on la construit dans un cadre général, en conservant à l’esprit que le sens de ce qui est fait doit être recontextualisé à la géométrie étudiée, celle où les trois sommets et les objets considérés sont intérieurs à l’ellipse.
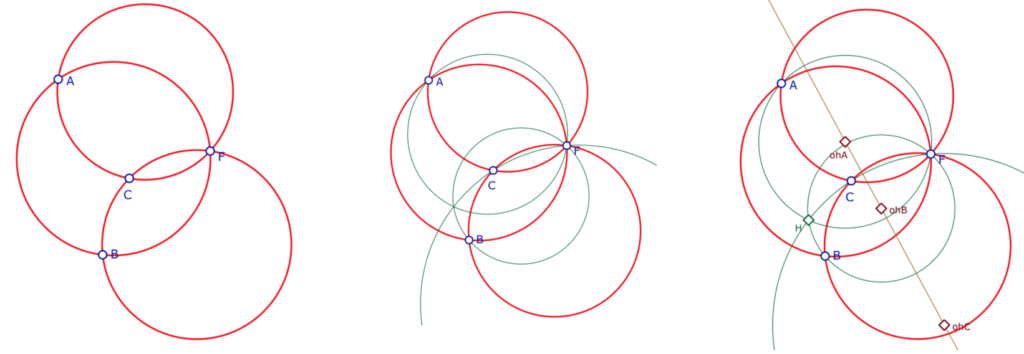
à gauche : trois cercles passant par \(F\) définissent le H-triangle \(ABC\).
au centre : chacun des cercles passant par un sommet (et par \(F\) pour être une H-droite) et orthogonal au cercle support du côté opposé est le support de la H-hauteur issue de ce sommet.
à droite : ces trois cercles orthogonaux sont concourants en un point \(H\) qui est le symétrique de \(F\) par rapport à la droite des centres des hauteurs du H-triangle \(ABC\).
Ce qui donne au sein de l’ellipse :
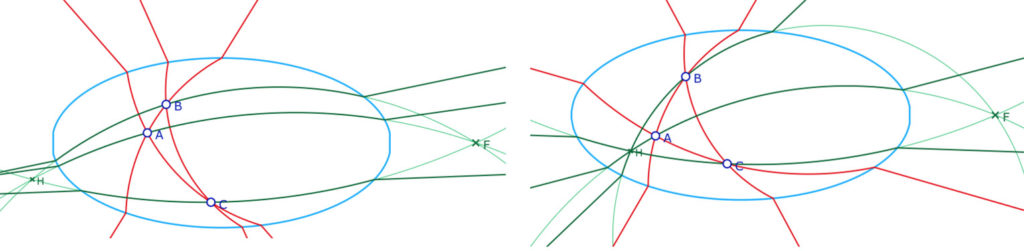
à gauche : quand \(H\) est à l’extérieur, il n’est pas sur les H-hauteurs
à droite : quand \(H\) est à l’intérieur de l’ellipse, il est sur toutes les hauteurs, c’est bien l’orthocentre du triangle \(ABC\).

à gauche : les milieux des côtés du H-triangle \(ABC\).
au centre : les H-médianes sont concourantes …
à droite : … en le symétrique de \(F\) par rapport à la droite euclidienne de centres des H-médianes.
Manipulations sur ces deux figures génériques …
On peut déplacer les points \(A, B, C\) et \(F\).
… et dans la version « Modèle de Hilbert », dans l’ellipse
Les H-hauteurs vertes, les H-médianes marrons de \(ABC\) intérieur à l’ellipse. Penser à faire sortir H de l’ellipse.
Preuve du résultat sur les hauteurs
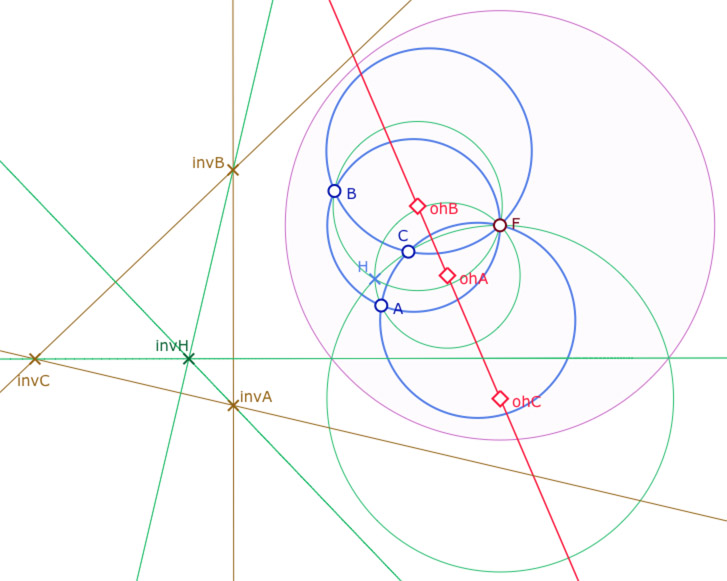
C’est une simple conséquence des propriétés de l’inversion. On sait que l’inverse d’un cercle passant par le centre de l’inversion est une droite et que l’inversion transforme un angle en son opposé et donc les cercles orthogonaux en droites orthogonales. Comme l’inversion est involutive (elle est bijective et est sa propre réciproque), l’existence de l’orthocentre d’un triangle euclidien assure celle du modèle des H-hauteurs des H-triangles (quand il est à l’intérieur de l’ellipse de Hilbert).Dans l’illustration ci-contre, on a pris un cercle centré en \(F\) et assez grand pour englober les trois cercles côtés du triangle \(ABC\) (ce n’est pas nécessaire c’est juste une question d’esthétique). L’intérieur du cercle a été coloriée pour un meilleur repère.
Dans la figure associée (s’ouvre dans un nouvel onglet) on peut modifier la taille du cercle d’inversion simplement en tirant dessus. On a ajouté des points \(M, N, P\) sur les cercles H-hauteurs, avec leurs inverses. On peut ainsi parcourir les trois inverses des hauteurs avec ces points. Le triangle euclidien des inverses a pour orthocentre le point \(invH\). Son image par l’inversion est donc un point appartenant aux trois cercles H-hauteurs, noté \(H=inv(invH)\). L’existence de \(H\) comme intersection des H-hauteurs de \(ABC\) assure aussi que les trois centres \(ohA, ohB, ohC\)de ces cercles, qui passent par \(H\) et \(F\) sont sur la médiatrice de ces deux points et donc alignés.
Preuve du résultat sur les médianes


Ouvrir et manipuler la figure associée dans un autre onglet
Utilisation de l’orthocentre pour un autre résultat spécifiquement non-arguésien
Nous allons utiliser l’existence du H-orthocentre d’un triangle intérieur à l’ellipse pour construire deux droites parallèles ayant deux perpendiculaires différentes issues d’un même point, ce qui est une situation différente de celle précédente construite à partir d’un rectangle ou on construisait des perpendiculaires communes à deux droites non parallèles.
On part donc d’un triangle intérieur à l’ellipse avec ses trois hauteurs et son orthocentre intérieur à l’ellipse. On se donne un point \(M\) sur la hauteur issue de \(B\) , extérieur à l’ellipse de façon à ce que le H-triangle \(MNP\) que l’on va construire soit un triangle euclidien. De \(M\) on mène la H-parallèle à \((AB)\). Pour cela on utilise les supports euclidiens des droites. Elle coupe la H-hauteur issue de \(A\) en \(N\). La H-parallèle à \((BC)\) issue de \(M\) coupe la H-parallèle à \((AC)\) issue de \(N\) en \(P\). A priori \(P\) n’est pas sur la H-hauteur issue de \(C\). C’est l’illustration de gauche le triangle \(ABC\) a ses côtés parallèles à ceux du triangle \(MNP\) par construction même de \(MNP\).
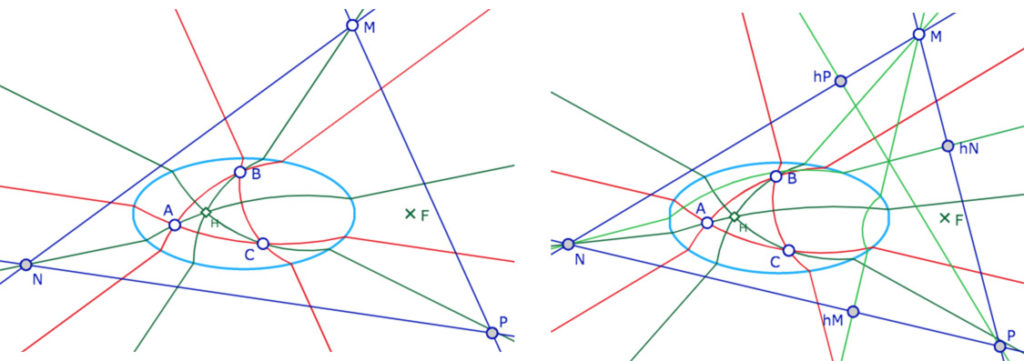
On trace ensuite les trois H-hauteurs de \(MNP\). La configuration est telle que les pieds des H-hauteurs sont les même que dans le cas euclidien, donc on peut tracer ces droites avec les macros du «cas 1». En pratique, on se place dans une configuration où le H-orthocentre de \(MNP\) existe car c’est aussi l’orthocentre euclidien de \(MNP\) euclidien. (illustration de droite)
Du point \(M\) on a donc mené
• (en vert foncé) la perpendiculaire à \((AC)\) issue de \(M\).
• (en vert clair) la perpendiculaire à \((NP)//(AC)\) issue de \(M\).
De \(M\) on a donc mené deux perpendiculaires différentes à deux droites parallèles. Idem pour \(N\).
Manipulation de la figure
Il faut activer les deux cases à cocher pour voir la propriété décrite. On peut déplacer \(A, B, C\) en gardant \(H\) dans l’ellipse.
Cependant, la figure n’est pas très stable : réalisée avec des macros transitoires, tous les cas ne sont pas traités.
Ouvrir la figure (plein écran, non restreinte) dans un autre onglet.
On ferait de même avec les bissectrices intérieures ou extérieures pour un triangle intérieur à l’ellipse, avec des arguments proches de ceux sur les hauteurs. Mais comme il y a une subtilité technique entre les bissectrices intérieures et extérieures, ce point est reporté à un post de blog.