Les figures de cette page sont légères, mais il y en a sept. S’il y a un message d’erreur, recharger la page.
Dans son article de 1902, Moulton proposait une géométrie non arguésienne avec pour axe de rupture de ses droites l’axe des abscisses, sur la base d’une réfraction sur un plan horizontal. Toutefois, depuis, on travaille plutôt avec une rupture sur l’axe des ordonnées. C’est ce que l’on fera ici.
Dans ces conditions, le plan de Moulton est alors ainsi défini :
• Les points du plan sont les points du plan euclidien usuel.
• La droite de Moulton \((AB)\), on dira « la M-droite \((AB)\)« , est :
– la droite euclidienne \((AB)\) si elle est verticale \((x_A=x_B)\).
– la droite euclidienne \((AB)\)si cette droite est à pente positive.
– Sinon, c’est la droite affine par morceau passant par \(A\) et \(B\) avec une seule rupture en un point d’abscisse nulle, tel que la pente de la demi-droite des abscisses positives soit le double de la pente de la demi-droite des abscisses négatives.
Dans toutes les illustrations suivantes, l’axe des ordonnées est en pointillés, gris clair : c’est l’axe de rupture des droites à pentes négative
Du point de vue de la géométrie dynamique, ce modèle est plus simple à implémenter que celui de Hilbert. Par exemple, contrairement au cas de Hilbert où il fallait une construction spécifique dans chacun des trois cas de droites (II, IE, EE), selon que les points définissant la droite sont à l’intérieur ou à l’extérieur de l’ellipse, et dans un cas avec nécessité de programmation, ici on peut arriver à faire une seule construction incluant les trois cas de la définition. Il en résulte que la M-droite est un véritable objet dynamique au sens où l’on peut construire, par macro-construction, la droite, la parallèle à une droite, on encore l’intersection de deux droites.
Organisation de la construction générale de la droite (AB)
Cette toute première partie est assez technique et n’intéressera que les personnes qui souhaitent voir, sur un exemple, comment on peut encapsuler trois cas particuliers de définition dans une seule construction géométrique. Elle intéressera surtout les personnes qui souhaitent en savoir plus sur le fonctionnement interne du logiciel utilisé. Elle est néanmoins présentée en préambule, pour que le lecteur, même sans entrer réellement dans les détails techniques, puisse avoir un aperçu des méthodes utilisées, et des points essentiels utilisés pour les constructions. Mais clairement on peut juste survoler cette partie.
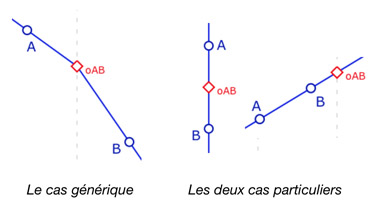
Par «générale» on entend une construction qui contient le cas que l’on dira «générique», c’est-à-dire celui de la pente négative, mais aussi des deux cas particuliers, celui de la pente positive et celui de la droite verticale. Dans le cas générique, la M-droite est la réunion de deux demi-droites d’origine un point \(o_{AB}\) de l’axe des ordonnées. Dans les deux autres cas, la droite euclidienne \((AB)\) usuelle est la M-droite associée. Mais pour réaliser un objet dynamique général, on choisit de conserver la réunion de deux demi-droites dans les trois cas. Il faut alors construire un unique point d’origine des deux demi-droites qui fonctionne dans tous les cas.
La démarche utilisée s’organise ainsi :
a – Calcul de l’ordonnée à l’origine du cas générique
b – En déduire les coordonnées générales de l’origine deux demi droites.
c – Calcul de la pente de la partie négative du cas générique
d – Calculs des coordonnées de points sur chacune des deux demi-droites.
On peut alors construire la H-droite comme réunion de deux demi-droites d’origine \(o_{AB}\) et passant par les points « généraux» calculés au point 4.
a – L’ordonnée à l’origine du cas générique
Le calcul élémentaire sur l’illustration ci-contre (pente double pour les abscisses positives) aboutit à la synthèse suivante :

Le JavaScript permet de synthétiser cette écriture par la combinaison linéaire des trois expressions algébriques affectées des coefficients booléens définis par les conditions imbriquées. Cela donne alors ceci :
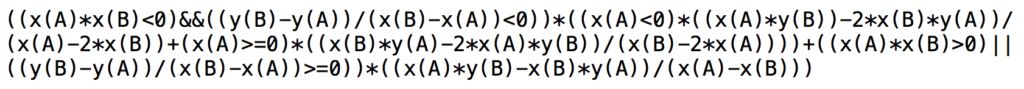
b – En déduire les coordonnées générales de l’origine deux demi droites
abscisse : si \(x_A=x_B\) alors l’abscisse \((x_{o_{AB}}\) est \(x_A\) sinon elle est 0.
ordonnée : si \(x_A=x_B\) alors \(y_{o_{AB}}=\frac{y_A+y_B}{2}\), sinon c’est l’expression présentée ci-dessus.
On utilise le test simplifié de JavaScript test?vrai:faux, sur l’abscisse et sur l’ordonnée, ce qui s’écrit ainsi :
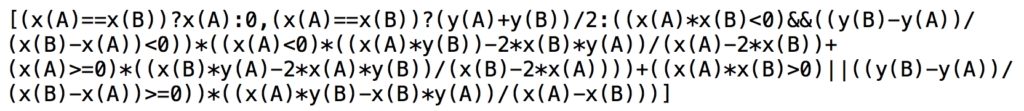
c – Calcul de la pente de la partie négative du cas générique (pABneg)
La pente de la partie négative du cas générique de la H-droite sera utilisée régulièrement dans de nombreux calculs. C’est donc intéressant, là encore, de chercher une expression compactée de cette pente qui rend compte de tous les cas. Nous laissons le lecteur vérifier que celle-ci convient.

d – Calculs des coordonnées de points sur chacune des deux demi-droites
On note dans la suite \(x_{o_{ABn}}\) et \(x_{o_{ABp}}\) deux points, le premier toujours dans la demi-droite d’abscisses négatives et le second dans celle d’abscisses positives, avec une adaptation de la définition pour une droite verticale. Sauf dans ce dernier cas, on peut toujours prendre les points d’abscisse -1 et 1 respectivement, comme dans les trois premières illustrations. L’intérêt d’utiliser ces points est qu’ils sont indépendants de la position des points \(A\) et \(B\).
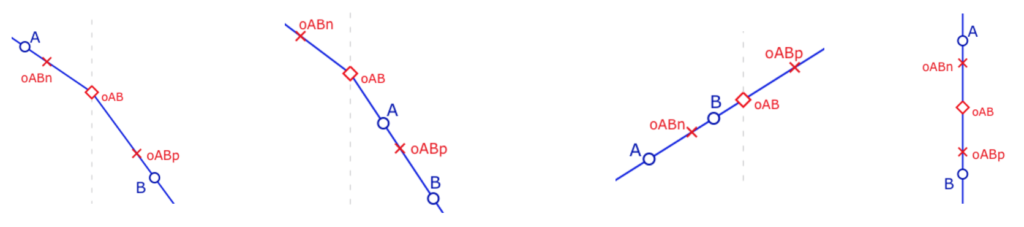
On utilise la même méthode que dans la construction du point \(x_{o_{AB}}\), en utilisant la pente pABneg. Ce qui donne :
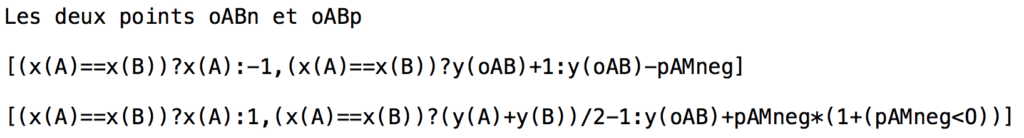
Et cela achève la construction générale de la M-droite \((AB)\), transformable en macro-construction.
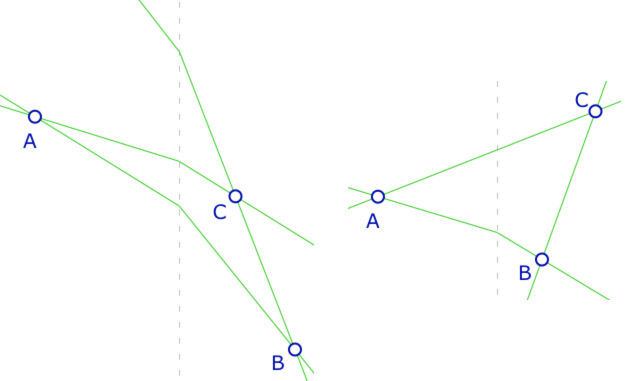
Manipulation d’un premier triangle de Moulton
On peut déplacer \(A, B\) et \(C\). Rendre \((AB)\) ou \((BC)\) verticale pour voir où sont les points de construction (case à cocher).
Premières applications
Dans cette partie, on regarde quelques « non-propriétés » affines de la géométrie du plan de Moulton.
Le plan de Moulton ne vérifie pas l’axiome III.5
Bien entendu, c’est le cœur de cette géométrie : elle et non-arguésienne car d’abord, elle ne vérifie pas cet axiome sur la congruence des angles en relation à celle des segments.
Comme pour le modèle de Hilbert, si cette géométrie est globalement non euclidienne, elle l’est localement, autour d’un point en dehors de l’axe des ordonnées. Il en résulte que, sauf si le point est sur l’axe des ordonnées, l’angle en un sommet est l’angle euclidien. De même la mesure de la longueur d’un segment est la somme des mesures des longueurs des segments euclidiens qui le compose.
On peut déplacer les points \(A, B, C\) et \(A’\). Toutefois, dans cette figure, seule la droite \((AB)\) – et donc le segment \([AB]\) –
est une vraie construction de Moulton. Il faut donc agir sur la figure en tenant compte de cette contrainte.
Illustration de la non vérification du théorème de Desargues
En mode «Moulton» – à l’ouverture de la figure – on peut agir sur tous les points nommés en bleu, en conservant toutefois leurs positions relatives
par rapport à l’axe des ordonnées ( \(I,A, A’\) à gauche, les autres à droite).
En mode «Affine» – case à cocher – seuls les points \(B, B’, C, C’\) sont modifiables.
Utilisation du parallélisme dans le plan de Moulton
Pour une meilleure fluidité de la lecture, on a reporté à une page de blog (non encore rédigée) le détail des constructions techniques diverses utilisées ici, comme les M-parallèles, le remplissage de M-triangle et de M-quadrilatère, le M-milieu.
Cette géométrie vérifiant tous les axiomes de Hilbert sauf le III.5 déjà mentionné. Il en résulte donc qu’il vérifie l’axiome d’Euclide sur les droites parallèles. Pourtant il n’y aucune propriété affine classique vérifiée.
Pas de théorème des milieux en général
Pour un M-triangle qui n’est pas un triangle euclidien, il n’y a généralement pas de parallélisme entre la droite du milieu et le troisième côté. Pour éviter d’aborder trop tôt l’orthogonalité, on vérifie le parallélisme par l’invariance (d’un côté) de la longueur d’un segment vertical, ce qui suffit puisque de chaque côté de l’axe des ordonnées, la géométrie est affine.

Dans les deux illustrations, les milieux sont pris sur des segments à pentes positives, donc ce sont les milieux euclidiens.
Figure : la M-droite des milieux dans un M-triangle
Déplacer \(M\) à droite et \(N\) à gauche de l’axe des ordonnées pour vérifier si les demi-droites à gauche et à droite sont parallèles ou non
(la longueur constante suffit). Agir sur les sommets \(A, B, C\) pour modifier le M-triangle.
Penser à rendre le M-triangle un vrai triangle euclidien pour voir qu’alors le théorème des milieux est vérifié.
Mais bien entendu, il est aussi très facile de construire des triangles de Moulton vérifiant le théorème des milieux. Dans l’illustration (de gauche) ci-dessous, on considère un segment de Moulton \([AB]\). On note \(I\) son M-milieu et \(I_e\) le milieu du segment euclidien \([AB]\). Sur la demi-droite euclidienne \([I_eI)\), et au delà du point \(oJ\) sur la droite horizontale passant par \(A\), on considère un point \(J\), puis on construit \(C\) le symétrique de \(A\) par rapport à \(J\).
Ainsi le M-triangle \(ABC\) a sa droite des milieux \((IJ)\) parallèle au côté \([BC]\).
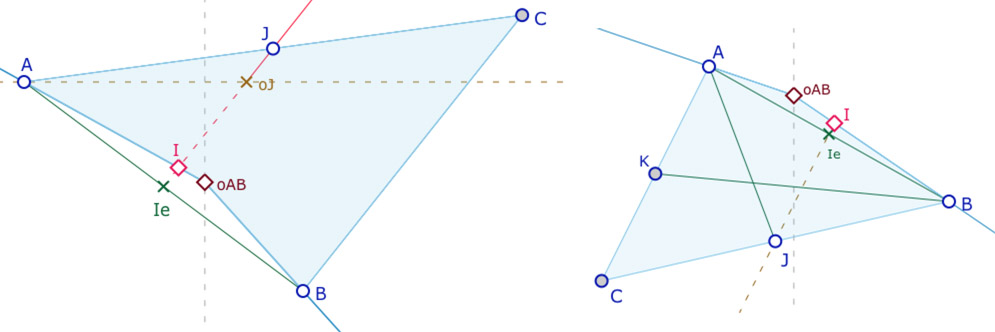
Sur l’illustration de gauche, basée sur la même démarche, il est clair que les médianes du M-triangle ne peuvent pas être concourantes, car le point d’intersection des M-médianes (aussi médianes euclidiennes) \([AJ]\) et \([BK]\) est sur la médiane euclidienne \([CI_e]\) et non pas sur la médiane de Moulton \([CI]\).
Pas de construction du milieu par le quadrilatère complet
La construction du milieu par la règle à bord parallèle n’est pas valide
Déplacer \(M\) pour voir que \(J\) n’est pas invariant. Dans le cas affine, \(J\) ne dépend pas non plus de \(C\).
Penser à tester le cas où la droite \((AC)\) est à pente négative.
Vérifier enfin le cas classique avec \(ABC\) euclidien, ie avec la droite \((AB)\) à pente positive (déplacer \(A\) et \(B\)).
Les parallélogrammes de Moulton (définis par deux couples de droites parallèles)
Dans cette figure, on agit sur les poignées des droites de base pour l’orientation du parallélogramme. Ce sont les points \(A\) et \(B\) et \(I\) et \(J\) .
Ensuite on agit sur la taille du parallélogramme par les points \(C\) et \(K\), de même abscisse que \(B\) et \(J\) respectivement.
Pas de construction possible du corps des coordonnées
C’est un des résultats théoriques important obtenu par Hilbert.
On se propose d’illustrer que, comme il n’y a pas de transitivité sur les parallélogrammes, il n’y pas de relation de Chasles sur les vecteurs associés, et donc de possibilité de construire une notion de coordonnées.
On se donne 3 points \(A, B, C\) et un point \(A_1\).
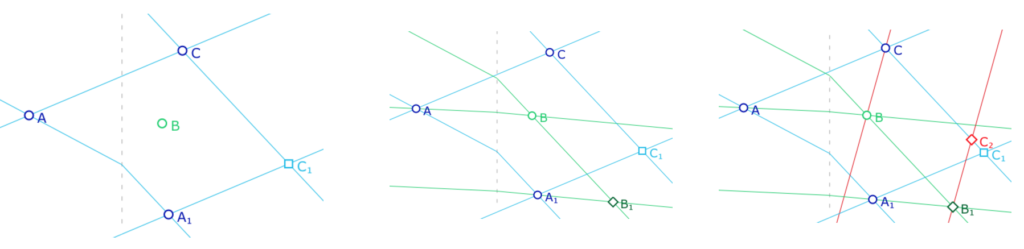
à gauche : on construit le point \(C_1\) tel que \(CAA_1C_1\) soit un M-parallélogramme.
au centre : on poursuit avec le point \(B_1\) tel que \(AA_1B_1B\) soit un M-parallélogramme.
à droite : on termine par le point \(C_2\) tel que \(CBB_1C_2\) soit un M-parallélogramme.

Et, alors, généralement, \(C_2\) est différent de \(C_1\).
Autrement dit, s’il y avait des M-vecteurs, en transformant les parallélogrammes en égalité de vecteur, on pourrait écrire \(\overrightarrow{CA}=\overrightarrow{C_1A_1}\), puis \(\overrightarrow{AB}=\overrightarrow{A_1B_1}\)(ici le segment \([AB]\) n’est pas euclidien), et on n’a pas – toujours avec les parallélogrammes – \(\overrightarrow{BC}=\overrightarrow{B_1C_1}\).
Ci-contre : le toit du théorème du même nom n’est pas pas vraiment ajusté … il y a de gosses fuites.
La figure suivante permet de construire pas à pas cette figure en 6 étapes avec 6 cases à cocher.
Figure de non constructibilité de M-coordonnées
Activer les cases à cocher dans l’ordre puis modifier les 4 points de base, \(A, C, A_1\) et \(B\).
Complément : page de présentation des macros, permettant de réaliser des figures dans le plan de Moulton