Avec la notion de segment elliptique, puis de triangle défini par ses segments, nous entrons désormais plus dans le champ des configurations. Pour définir les segments, on revient sur la sphère. Si on considère une sphère unité, la longueur d’un grand cercle est \(2\pi\), c’est la longueur, constante, de toutes les géodésiques de la sphère. Pour la géométrie elliptique, on ne considère qu’un demi cercle.
On conserve, pour la géométrie elliptique, les longueurs sur la sphère. Les géodésiques étant des cercles centrés au centre de la sphère, la longueur entre deux points \(A\) et \(B\) de la sphère est proportionnelle – on choisit même « égale » à l’angle au centre \(\angle AOB\). Mais cette définition initiale n’est pas exploitable par projection dans le plan.
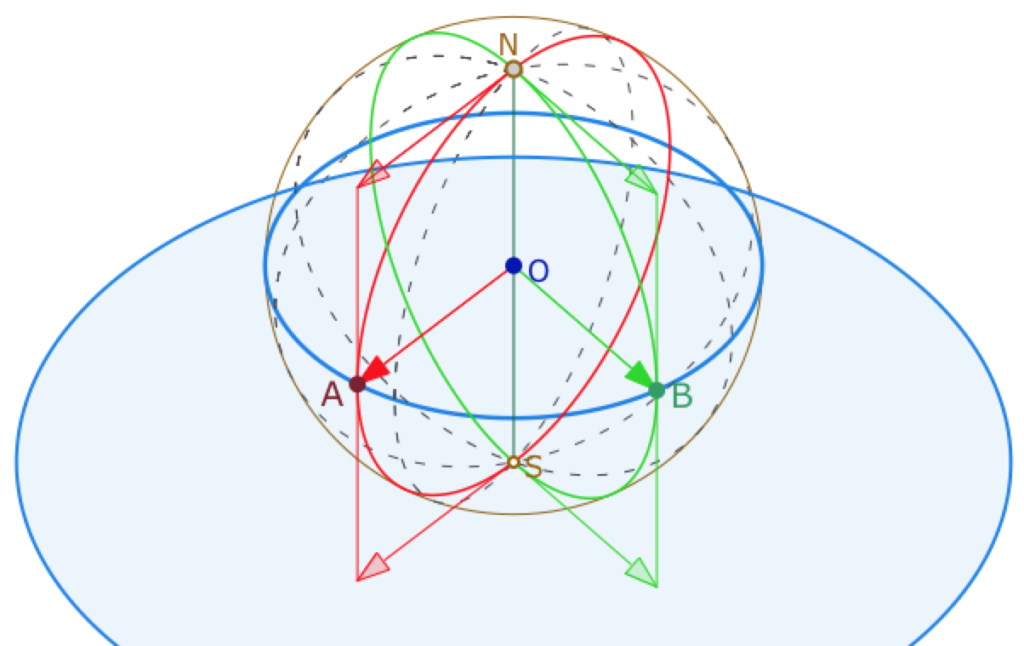
On peut remarquer que cet angle, par les tangentes aux géodésiques-cercles – les tangentes en \(N\) ci-dessus – est l’angle du triangle sphérique, issu du pôle de la droite \((AB)\). On le voit ci-dessus dans le cas générique (car, à une rotation près, un grand cercle est un équateur) où \(A\) et \(B\) sont sur l’équateur et le pôle de la droite est le pôle nord de la sphère. L’intérêt de cette nouvelle interprétation est qu’elle est transférable dans le contexte elliptique par projection stéréographique. Et comme la projection est conforme, on conserve l’angle depuis le pôle comme mesure de la longueur d’un trajet elliptique associé à celui sur la sphère. Ainsi une droite elliptique a pour longueur \(\pi\) : si \(B\) est le symétrique de \(A\) par rapport à \(O\), les vecteurs tangents verts et rouges sont opposés.
Plus généralement, la longueur entre deux points est mesurée par l’angle en \(P\) du triangle \(APB\) où \(P\) est le pôle de \((AB)\). C’est vrai sur la sphère (l’angle \(\angle AOB\) est aussi l’angle en \(N\) du triangle sphérique \(ANB\)), et par projection dans le modèle plan de Klein.
Segment – critère géométrique – critère numérique
Disposer d’une mesure de longueur va surtout permettre de simplifier les constructions des segments. On pourrait les obtenir sans cela, les constructions seraient juste plus longues – elles le seront déjà assez.
Segment – version géométrique
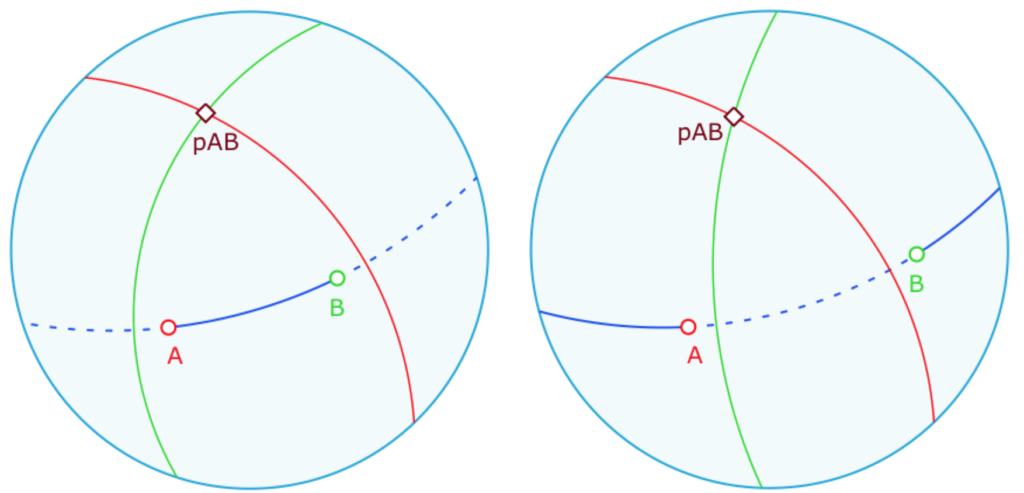
En effet, soient \((AB)\) une droite. Les polaires de \(A\) et \(B\) se coupent en \(P\) le pôle de \((AB)\). Qu’est ce que le segment elliptique [AB] ? La droite étant bornée c’est celui des deux chemins de A vers B sur (AB) qui est le plus court.
On a vu que, dans un triangle tripolaire, les côtés du triangle sont des moitiés de droites. Ainsi, sans aucun calcul de longueur, on peut dire que la partie de (AB) qui est le segment [AB] est celle qui ne coupe pas les polaires de A et B. Ci-contre on voit les deux formes du segment \([AB]\) … à rapporter sur la sphère.
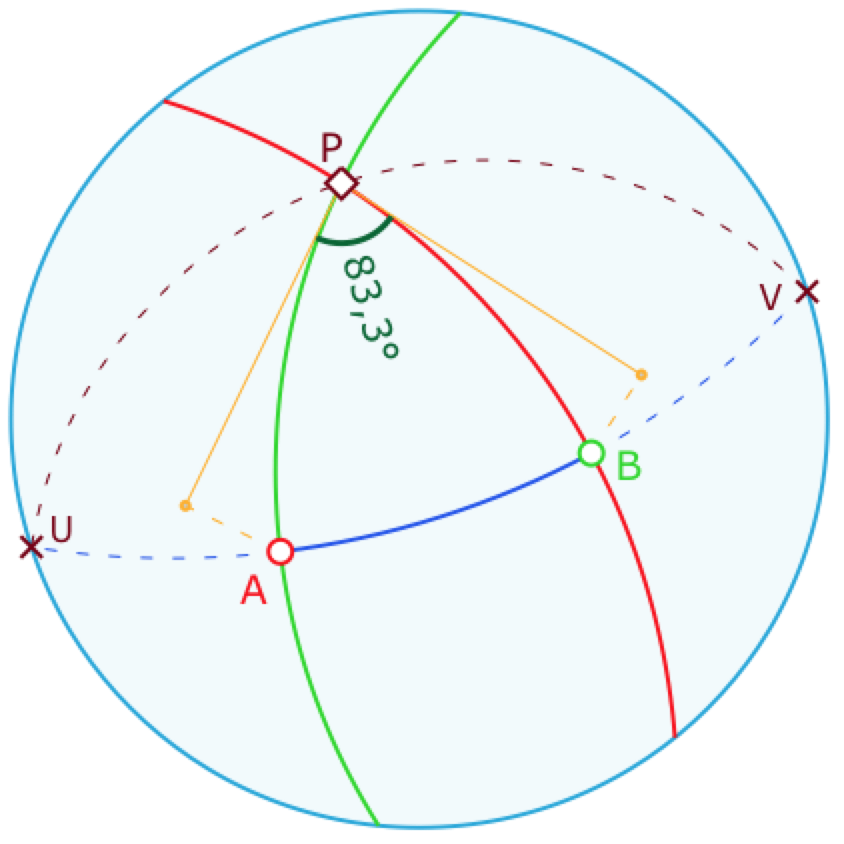
Segment – version numérique
Il y a ici une représentation prégnante liée au modèle : on entend par « aller de \(A\) à \(B\) », de fait, le chemin intérieur au cercle – le « segment interne » – ce qui défini une longueur implicite à partir de l’angle en P des droites \((PA)\) et \((PB)\) comme détaillé ci- contre.
En s’installant dans une mesure en degré, il y a donc la longueur de \(A\) à \(B\) et la distance \(d(A,B)\), avec \(d(A,B) = min(long(A,B), 180-long(A,B))\).
Tout comme le fait que les géodésiques de la sphère sont ses grands cercles, de même, que d soit une distance n’est pas un résultat immédiat.
Le segment [AB] comme intersection des deux demi-droites [AB) et [BA)
De manière un peu surprenante – car cette géométrie est fondamentalement non orientée – avec la définition que nous avons donné à la notion de demi-droite, on retrouve que le segment [AB] est bien la partie commune aux demi-droites \([AB)\) et \([BA)\). Dans les illustrations suivantes, on trace \([AB)\) et \([BA)\) dans les trois cas possibles de \([AB)\). En marron \(A\) et sa polaire, en vert \(B\) et sa polaire.
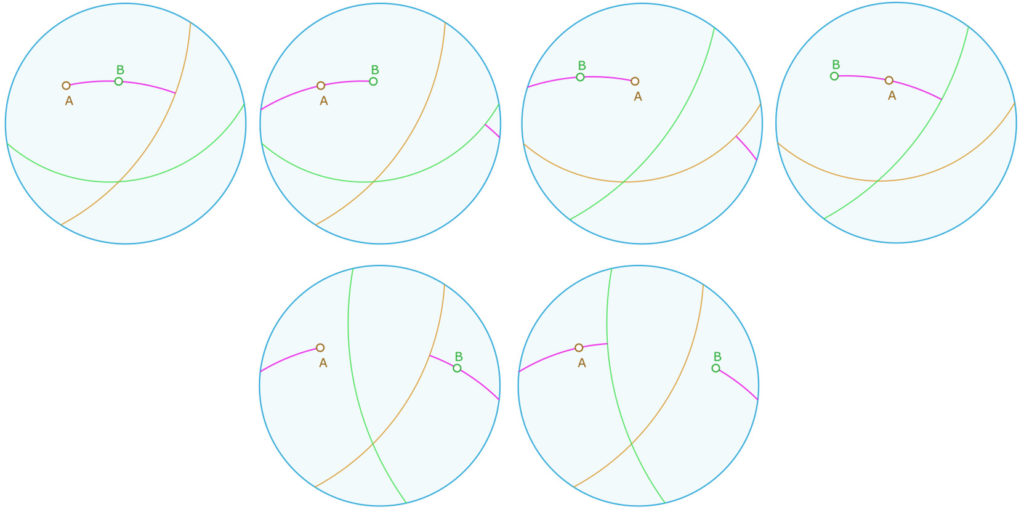
Les deux cas du haut (les deux illustrations de gauche et les deux de droite) correspondent au cas où la longueur \(AB\) est aussi la distance \(d(A,B)\). Les deux cas du bas illustrent la troisième possibilité, où \(A\) et \(B\) sont de part et d’autre des deux polaires, et donc la distance \(d(A,B)\) est réalisée par le complémentaire de la longueur \(AB\) sur la droite.
Si le segment elliptique est toujours un objet connexe, sa représentation peut l’être (ce sont les cas du haut) ou non (cas du bas). La représentation d’un segment est connexe quand la longueur \(AB\) est aussi la distance \(d(A,B)\).
Le segment elliptique est un exemple où la représentation d’un objet dans un modèle peut avoir des propriétés topologiques différentes de l’objet. On l’avait vu sur les droites de \(STS(13)\), mais c’était un cas de géométrie finie.
Le segment elliptique \([AB]\) comme intersection des demies droites \([AB)\) et \([BA)\).
\(ChBA=0\) pour la demi-droite \([AB)]\), \(ChBA=1\) pour la demi-droite \([BA)\), et \(ChBA=2\) pour le segment \([AB]\).
Cette figure est plus un «dessin dynamique» au sens où les objets ne sont unifiés (il faut 5 arcs pour une demi-droite.
Triangle – Axiome de Pasch

L’axiome de Pasch (1882) traite de l’intersection d’une droite et d’un triangle. Il dit que si une droite coupe un côté d’un triangle, en autre point qu’en un sommet, alors il coupe un autre côté du triangle. Pasch s’est aperçu qu’Euclide utilisait ce résultat implicitement.
Figure d’exploration
1. Commencer par construire les 3 segments [AB], [BC], et [CA] avec la macro associée
(les macros sont par ordre alphabétique, il faut parcourir le menu des macros pour voir Seg Ell)
2. Puis tracer la droite (MN)
3. Déplacer les points A, B, C pour voir les formes d’un triangle elliptique
4. Puis explorer l’axiome de Pasch en géométrie elliptique.
Préférer utiliser cette figure finalisée (dans un nouvel onglet)
Deux types de triangles elliptiques
On pourrait visuellement distinguer quatre types de triangle, comme proposé ci-dessous. Mais en fait, il n’y a que deux types : celui des deux illustrations de gauche, au comportement euclidien pour l’axiome de Pasch, et celui des deux illustrations de droite qui ne vérifient pas l’axiome de Pasch.
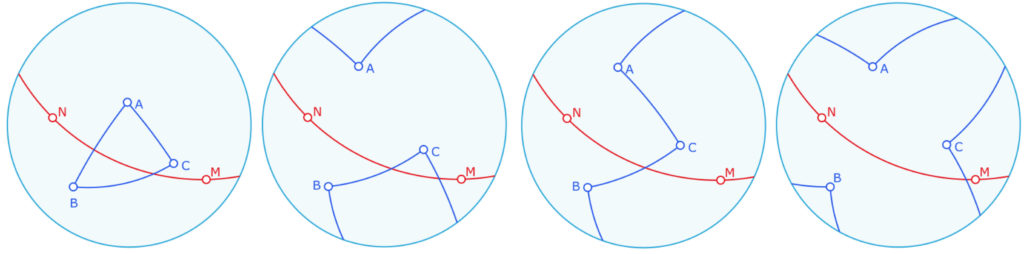
Dans les deux cas, les deux configurations proposées n’en sont qu’une elliptiquement parlant, la distinction ne venant que de spécificités du modèle. Dans le cas euclidien, à gauche, tout comme le cas elliptique, à droite, on passe d’une représentation à l’autre par une simple rotation de l’équateur sur la sphère.
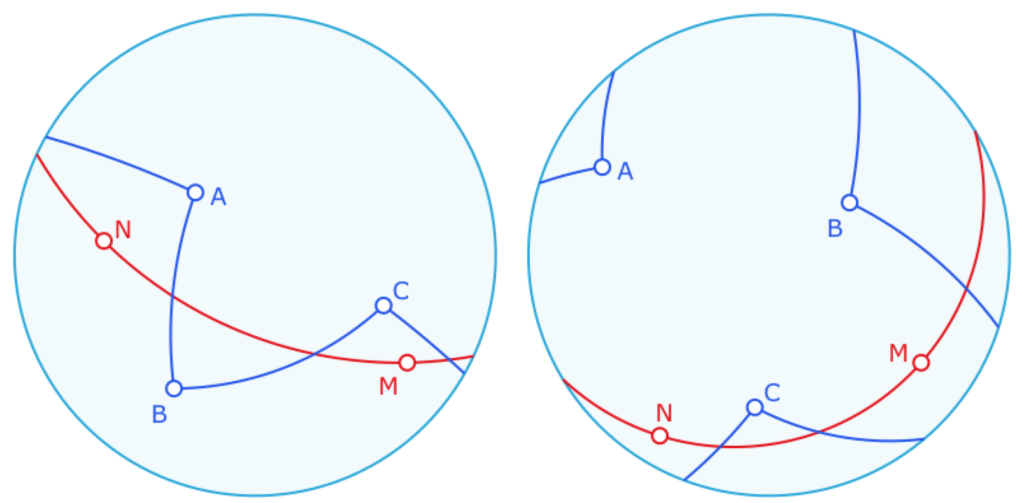
Donc l’axiome de Pasch n’est pas vérifié en géométrie elliptique. Ci-contre, la droite \((MN)\) coupe les 3 côtés du triangle.
Dans certaines éditions des éléments d’Euclide, il est implicitement utilisé dès la proposition 6, et donc tout ce qui suit, pratiquement, n’est pas elliptique.
L’axiome de Pasch est en particulier utilisé pour déterminer le nombre d’intersections de deux cercles. Sans l’axiome de Pasch, ce nombre n’est plus limité à deux.
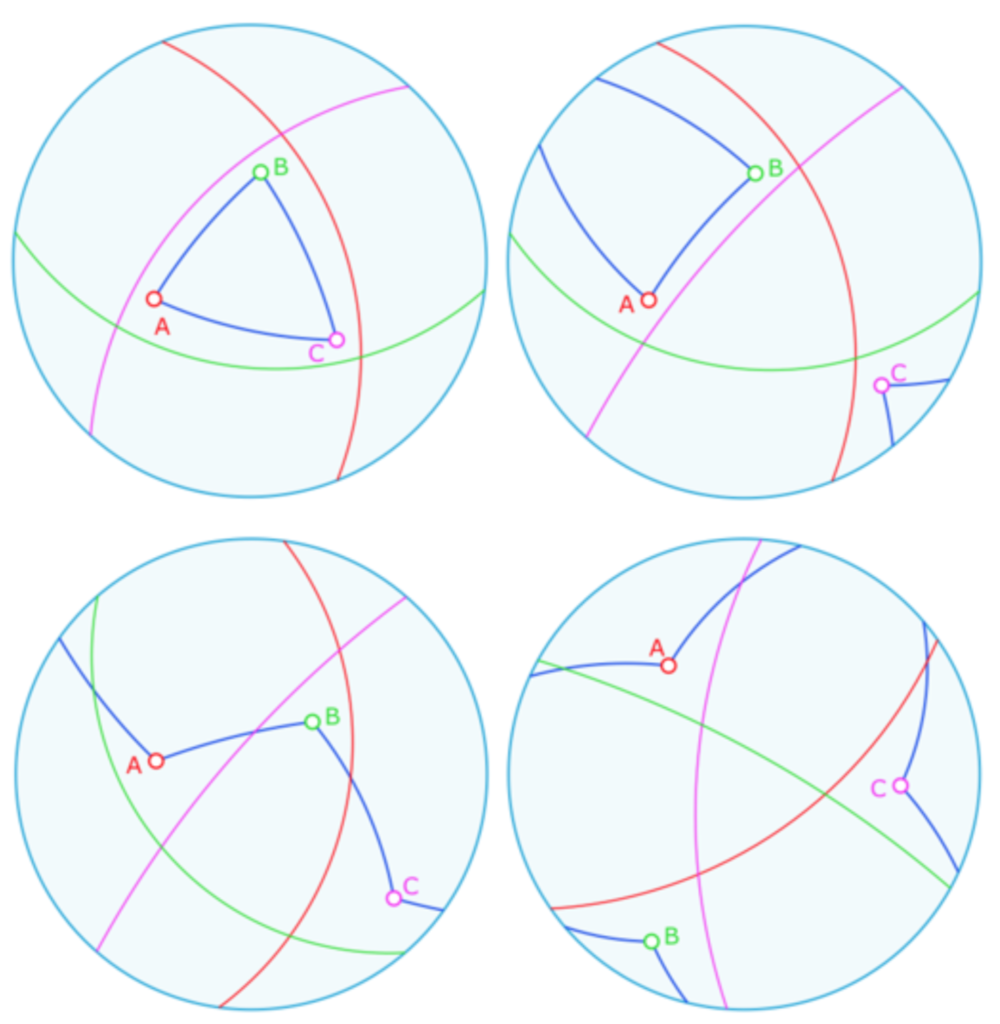
Types de triangle et polaires des sommets
Les trois polaires de trois points délimitent 4 régions du plan elliptique, ci contre celle du centre et les trois autres par identifications des extrémités.
Type euclidien : c’est un triangle qui est entièrement dans une composante connexe délimitée par les trois polaires. On dit qu’il est « relevable sur la sphère » pour dire, comme dans les deux illustrations du haut, qu’à une rotation près c’est l’image d’un triangle de la sphère placé dans un seul hémisphère.
Type elliptique : si un segment traverse la polaire d’un sommet, les trois segments traversent la polaire d’un sommet. On a donc les trois sommets dans 3 composantes connexes différentes. Ce type de triangle n’est pas relevable en un triangle sphérique car quelque soit la rotation effectuée, il y aura toujours une intersection d’un segment avec une polaire.
Ces illustrations ne rendent pas compte de toutes les configurations, même si elles sont équivalentes.
Il reste un cas très particulier, Si \(A, B\) et \(C\) sont alignés, les trois polaires sont concourantes en le pôle de la droite d’alignement.

Exploration sur les configurations dans le modèle utilisé des deux types de triangle elliptique
1. La figure d’ouverture est bien un triangle qui a une intersection avec chacune des trois polaires
2. Manipuler \(A, B, C\) pour explorer toutes les possibilités
3. Éventuellement utiliser d’autres macros-constructions proposées dans la figure