Depuis que l’on n’enseigne plus la géométrie projective, ce n’est pas courant de voir l’infini de près. Travailler dans un modèle borné – ici de la géométrie euclidienne – est l’occasion de réfléchir à ce que peut apporter de travailler dans ces modèles. C’est aussi l’occasion d’apprendre à ne pas déduire des propriétés du modèle des généralités de la géométrie étudiée. Voyons cela sur un exemple.
Tout d’abord remarquons que, dans le modèle euclidien borné, toutes les perpendiculaires à une droite ont les Tout d’abord remarquons que, dans le modèle euclidien borné, toutes les perpendiculaires à une droite ont les deux mêmes points à l’infini : les points de la direction à l’infini des perpendiculaires à la droite.
Une conséquence intéressante est dans la construction des paraboles dans ce modèle, qui donne un éclaircissement intéressant à cette propriété projective bien connue : la parabole est une conique tangente à la droite de l’infini. C’est ce que l’on se propose de faire dans cette page.
Droite de Steiner et parabole tritangente à un triangle
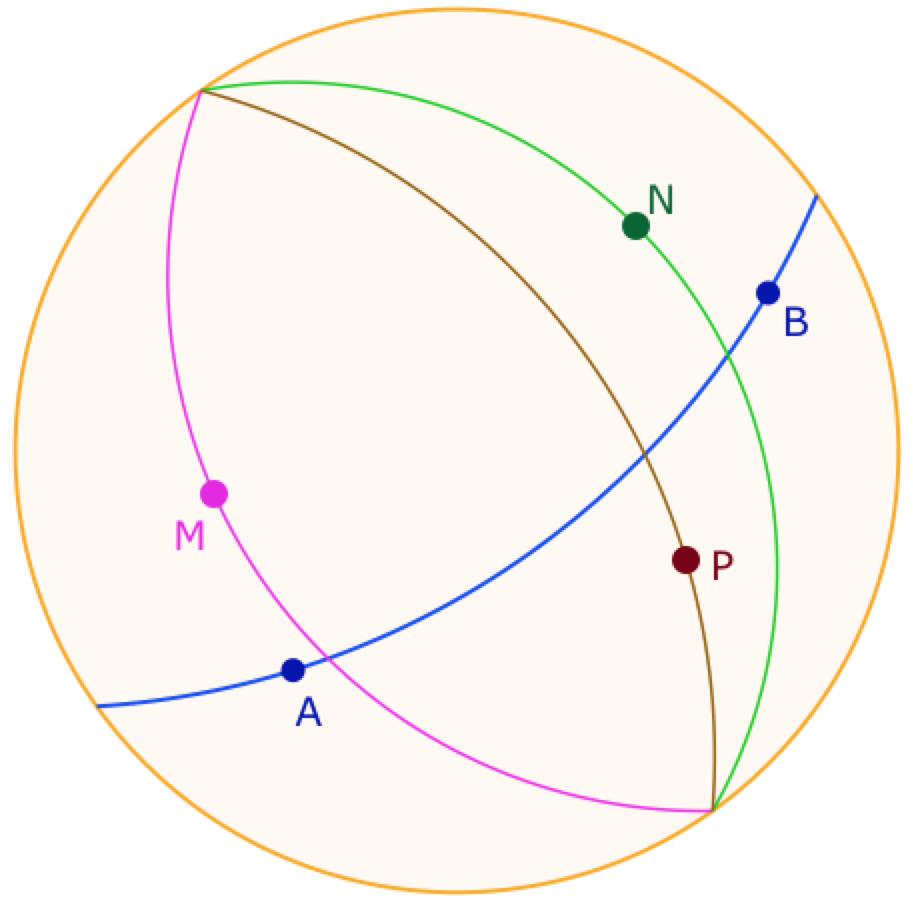
Faisons la construction dans une situation dynamique : soit un triangle \(ABC\). Alors les symétriques d’un point \(M\) par rapport aux trois côtés du triangle sont alignés si et seulement si \(M\) appartient au cercle circonscrit à \(ABC\).
Par construction, la parabole de foyer ce point \(M\) du cercle et de directrice cette droite dite droite de Steiner associée à M est tritangente au triangle.
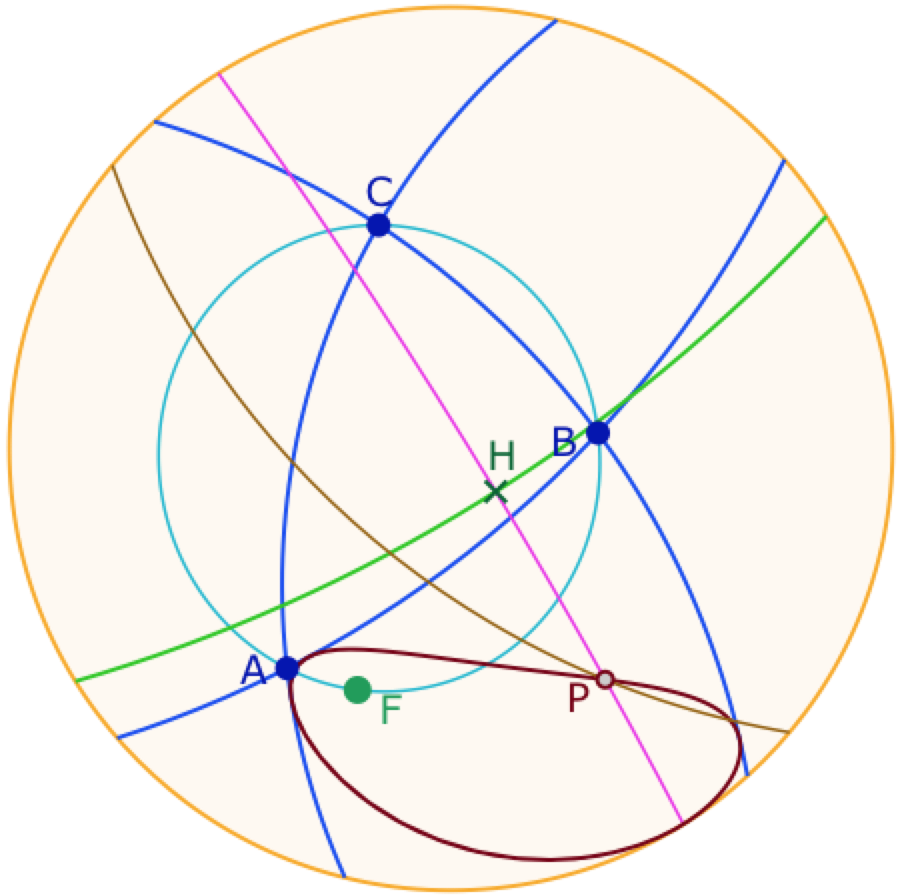
Voyons cette construction dans le cas du modèle borné. Pour construire la parabole, on se donne un point \(H\) sur la directrice, la droite de Steiner associée à \(F\) (droite verte ci-contre). Le point \(P\) de la parabole est l’intersection de la perpendiculaire en \(H\) (rose) à la directrice et la médiatrice (marron) de \(H\) et \(F\), le foyer de la parabole sur le cercle circonscrit à \(ABC\).
Alors le lieu de \(P\) est la parabole précédente, mais ici elle est tangente au cercle horizon ce qui exprime le résultat de la classification projective des coniques : les hyperboles coupent la droite de l’infini en deux points, la parabole n’a qu’un point de contact avec la droite de l’infini, et lui est donc tangente.
Dans la figure suivante vous pouvez d’abord manipuler la figure illustrée ci-contre, déplacer \(H\), pour voir \(P\) aller vers l’infini sur la parabole tangente à l’horizon, déplacer \(F\) aussi.
Puis vous pouvez cocher la case « Préparer l’animation » qui cache les éléments non essentiels, pour, ensuite, animer le point \(F\). Pour cela, activer le mode standard (sélectionner la flèche gauche du tableau de bord), puis, faire un clic droit (souris) ou touché prolongé (tablette) sur le point \(F\), et choisir le ressort (icone de droite ci-dessous). Y mettre une vitesse de 3% seulement cela suffit. Apprécier le résultat.
Point de Miquel d’un quadrilatère complet et
parabole quadritangente associée
Quand on applique le théorème du Pivot à un triangle formé de trois droites, un cas particulier intéressant est celui où les point \(M, N\) et \(P\) sont alignés. L’ensemble des trois droites d’un triangle et une droite qui le coupe comme la droite \((MN)\) s’appelle un quadrilatère complet.
Alors le point d’intersection (pivot) des trois cercles est un point du cercle circonscrit. Il s’appelle le point de Miquel. Et la parabole de foyer ce point et de directrice sa droite de Steiner est non seulement tritangente au triangle mais aussi à la droite \((MN)\), elle est donc quadritangente au quadrilatère complet.
Dans ces illustrations, le cercle circonscrit est bleu, les cercles du pivot sont violets. On voit que la parabole est bien tangente à la droite \((MN)\). Elle est bien entendu toujours tangente à la droite de l’infini.
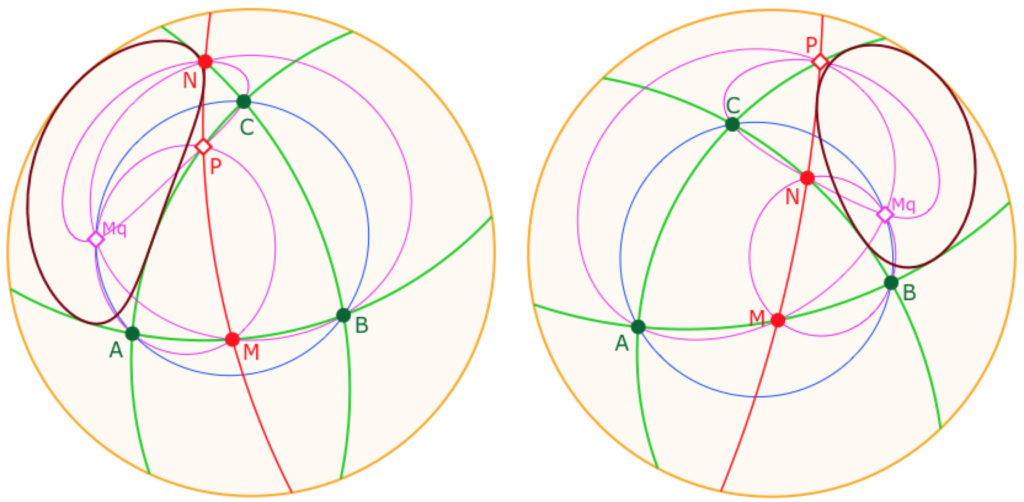
A gauche on a placé le point \(N\) en dehors du segment. On agit sur \(M\) et \(N\), le point \(P\) est construit.
Remarque sur la figure suivante : Quand on déplace l’un des points \(A, B\) ou \(C\) les déplacements de \(M\) et \(N\) ne sont pas «barycentrique dans le modèle borné». Il faut donc ajuster \(M\) et \(N\) qui vont à l’infini, ce qui perturbe la figure. En pratique, la figure n’est pas très stable quand une des droites change d’orientation en particulier. Il faut remettre \(M\) et \(N\) à distance bornée. Penser à éviter l’artefact de la directrice (non tracée ici) proche d’un diamètre.