Exemple d’une lecture absolue de construction
géométrique : la construction de Malfatti
Certaines constructions géométriques faisant appel à des propriétés issus de la cocyclicité peuvent avoir une lecture absolue, et d’autres non. Nous reviendrons en détail sur ce point dans une partie traitant de l’axiomatique de Bachmann. Dans plusieurs menu de ce site, nous allons utiliser une construction géométrique non triviale, comme fil rouge, pour la construire dans les trois géométries, et donc par conjugaison, ici, dans le modèle borné euclidien. Nous avons retenu le problème de Malfatti.

Il s’agit de construire trois cercles, inscrits chacun dans un angles d’un triangle, et tels qu’ils soient tous les trois deux à deux tangents.
Il existe de nombreuses preuves de constructions analytiques, qui ne nous intéressent pas ici. C’était le cas de celle de Malfatti. La première construction géométrique est due à Steiner, basée sur l’inversion. Nous allons ici faire une lecture « absolue » de la construction proposée par Jean Claude Carrega dans son ouvrage « Théorie des corps : la règle et le compas » (Ed. Hermann – 1981). Pour cela, il faut regarder la méthode de construction de manière non euclidienne, en tout cas sans cocyclicité.
Etape 1 : On commence par construire le centre \(I\) du cercle inscrit du triangle \(ABC\), puis les cercles inscrits des trois triangles \(AIC, BIA\) et \(CIB\). Ci-dessous à gauche on a nommé \(c_A, c_B\)et \(c_C\) leurs centres (\(c_X\) pour le cercle opposé au sommet \(x\))

Etape 2 : les bissectrices du triangle \(ABC\) sont donc, par construction, des tangentes communes à ces cercles pris deux à deux. On s’intéresse ensuite à l’autre tangente commune intérieure de ces trois couples de cercles. Ce sont les trois droites roses ci-dessus à droite.
Une lecture absolue de leurs constructions consiste à remarquer qu’on les obtient par symétrie par rapport aux droites des centres (en cyan ci-contre) des bissectrices de \(ABC\) : il n’y a pas besoin de construire les cercles, ils n’ont été ici qu’un argument euclidien d’illustration dont on peut se passer.
Alors ces trois tangentes communes (des cercles pris 2 à deux) sont concourantes en un point \(Q\). Ce résultat est absolu, se démontrerait par des propriétés sur les faisceaux (notion définie dans les menus suivants).
Etape 3 : Chacune de ces droites coupe respectivement les côtés du triangle en \(R, S\) et \(T\) : l’autre tangente commune aux cercles de centre \(c_A\) et \(c_B\) coupe \((AB)\) en \(R\), etc. (illustration de gauche)
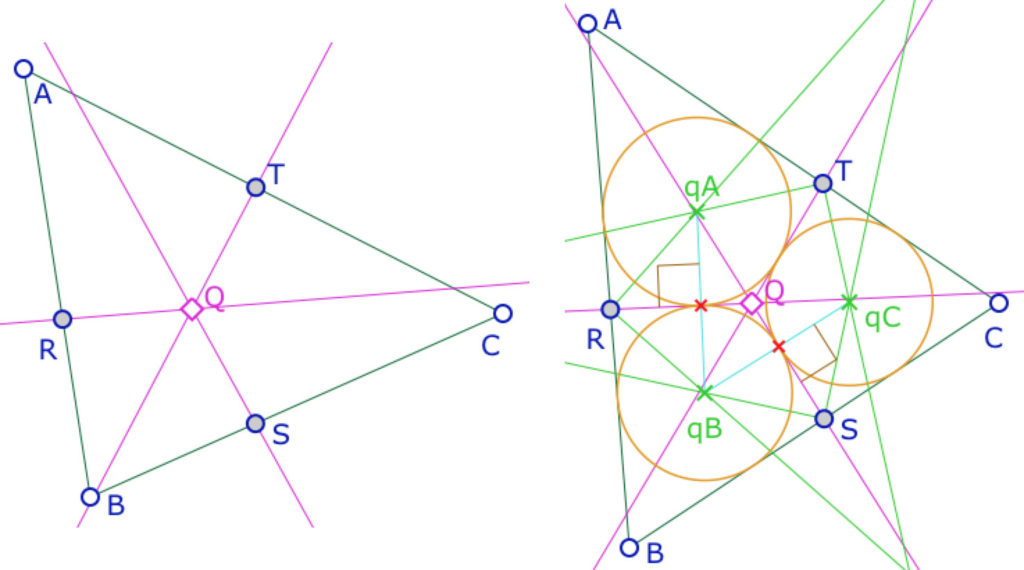
Etape 4 : alors les quadrilatères \(ARQT, BSQR\) et \(CTQS\) sont circonscriptibles et les cercles inscrits à ces quadrilatères sont les cercles de Malfatti.
Autrement dit les « autres tangentes communes intérieures » (roses) des cercles inscrits initiaux sont des tangentes communes (et axes radicaux dans le cas euclidien) des cercles solutions.
Deux autres résultats sur la construction de Malfatti sont proposées dans la figure euclidienne suivante.
Pour le second point, on peut dézoomer la figure. Pour cela rester en mode consultation (aucun outil sélectionné),
et utiliser 2 doigts (tablette ou trackpad). Sur ordinateur, fonctionne même avec un outil sélectionné.
Construction dans la version bornée du disque euclidien
On transforme la figure précédente en macro construction. Cela permet de l’appliquer directement aux points images des sommets par la macro DE vers E. Puis on renvoie les cercles (un point sur chaque cercle par la macro E vers DE). On termine la construction simplement par des lieux : les six cercles (cas second lieu de jAjima) sont les lieux d’un point pris sur les cercles de la figure issue du transformé du triangle.
Cette construction sera reprise dans le cadre de la géométrie hyperbolique, dans les trois modèles présentés (DP, PS, PSH), puis de la géométrie elliptique.