Cette page est consacrée aux principaux pinceaux remarquables, dont les médiatrices, les bissectrices, ou les hauteurs et quelques conséquences. Comme déjà mentionné dans d’autres pages du site, la question des médianes, dans ce cadre très général, est plus complexe à traiter et nécessite d’autres outils développés plus loin dans la théorie. Dans cette page, on utilise les premiers résultats de base (th 1 à 9) naturellement, mais aussi ceux autour du théorème de Hjelmslev et les théorèmes sur les pinceaux autour de la transitivité.
Les théorèmes, énoncés dans un cadre très général – en particulier indépendamment de la construction d’un corps de nombres associé à la géométrie – introduisent des hypothèses sur l’existence de certaines droites qui peuvent ne pas exister selon la richesse de la géométrie. Bachmann parle de « mobilité dans le plan », notion sur laquelle nous reviendrons dans une page consacrée aux corps associés aux géométries dégagées selon les axiomes ajoutés. Par exemple sur la géométrie minimale de Bachmann, le plan euclidien sur \(\displaystyle \frac{\mathbb{Z}}{3\mathbb{Z}}\), à 9 points et 12 droites, déjà présenté ici, par chaque point passent 4 droites, par paire, deux à deux orthogonales, chaque paire étant bissectrices de l’autre. Mais deux droites incidentes à un point et non orthogonales n’ont pas de bissectrices car il n’y a pas assez de droites.
Dans le contexte de nos illustrations hyperboliques et elliptiques, dans les modèles euclidiens construits sur \(\mathbb{R}\), il n’y a pas problème de mobilité : en général ces droites existent car il existe toujours une médiatrice de deux points, et donc un centre de symétrie de deux points, ou encore deux droites ont toujours (au moins) un axe de symétrie. Nous commenterons souvent ces illustrations avec la culture déjà acquise des menus précédents DP et ELL même si les objets mis en évidence (essentiellement des cycles) ne sont pas encore développés dans la description de l’axiomatique de Bachmann.
Médiatrices d’un triangle
Th 20 : Médiatrices d’un triangle
Soit \(ABC\) un triangle. S’il existe deux droites \(u\) et \(v\) telles que \(A^u=B\) et \(B^v=C\), alors il existe une droite \(w\) telle que \(u, v, w\) soient en pinceau et que \(A^w=C\).
Preuve : Soit (par Th 13, sur l’existence d’une droite d’un pinceau passant par un point) la droite \(g\) du pinceau \(\mathscr{P}_{uv}\) passant par \(B\). Alors \(ugv\) est une droite \(w\) et on a : \(A^w=A^{ugv}=B^{gv}=B^v=C\)et de plus, le produit est une droite du pinceau de par les propriétés déduites de la transitivité.
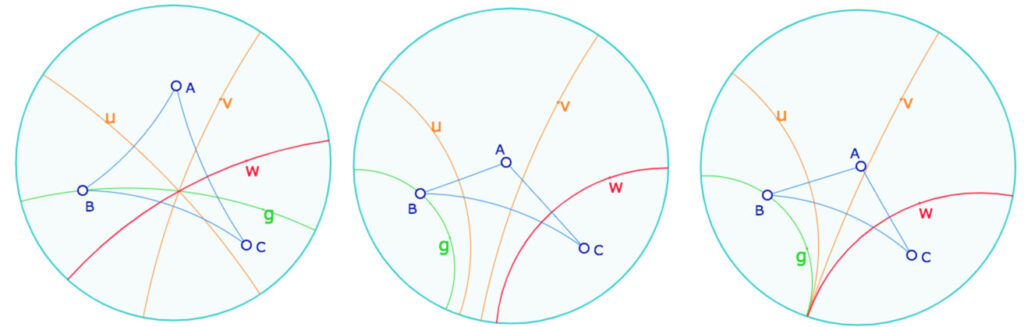
Illustration des trois types de pinceau dans le contexte hyperbolique.
Lancer cette figure dans un nouvel onglet. Le point \(C\) est aimanté par un horicycle passant par \(A\) et \(B\) pour que le pinceau puisse être réellement à centre.
Note sur la manipulation des figures de toute cette page
Les noms des droites sont en fait donnés par des points. En manipulant la figure, rapidement ces noms des droites (\(u, v, w, g\) ci-dessus) vont sur le cercle horizon. Pour les changer de place, il suffit de se rapprocher de ces noms, et quand ils sont surlignés, on peut les prendre à la souris et les déplacer.
Dans le contexte elliptique, il n’y a qu’un type de pinceau : les pinceaux à centre. On sait qu’il y a deux médiatrices pour deux points donnés et donc deux droites \(u\) (\(u_1, u_2\)) et deux droites \(v\) (\(v_1, v_2\)) ci-dessous … et donc quatre droites \(g\) (de la preuve): \(g_{11}, g_{12}, g_{21}\) et \(g_{22}\) … mais il n’y a bien que deux médiatrices \(w\) de \(A\) et \(C\) et non pas quatre. Voici une illustration :
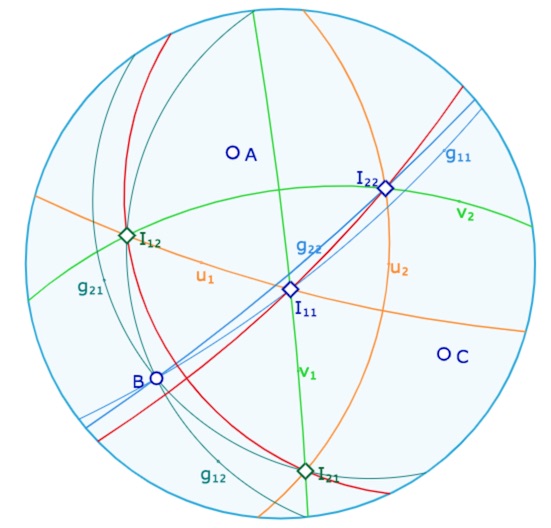
Les droites du théorème 20 dans le cas elliptique
Les droites \(w_{11}\) et \(w_{22}\) sont confondues: c’est la droite \((I_{11}I_{22})\).
Les droites \(w_{12}\) et \(w_{21}\) sont confondues: c’est la droite \((I_{12}I_{21})\).
Lancer la figure associée dans un nouvel onglet.
Les 4 intersections \(I_{11}, I_{12}, I_{21}, I_{22}\) sont les centres des 4 cercles circonscrits à \(ABC\). Des figures plus abouties ont déjà été proposées dans cette page du menu ELL.
Bissectrices de trilatères
La question des bissectrices est très intéressante dans le cas hyperbolique car les bissectrices peuvent ne pas être en pinceau. Commençons par un premier résultat élémentaire.
Th 21a : bissectrices en pinceau à centre
Soient \(a, b, c\) trois droites. S’il existe deux droites \(u\) et \(v\) telles que \(a^u=b\) et \(b^v=c\) et s’il existe \(J \mid u, v\), alors il existe une droite \(w\) telle que \(a^w=c\), et \(u, v, w\) sont en pinceau.
Preuve : Soit \(g\) la perpendiculaire à \(b\) incidente à \(J\). Alors \(ugv\) est une droite \(w\) et on a : \(a^w=a^{ugv}=b^{gv}=b^v=c\).
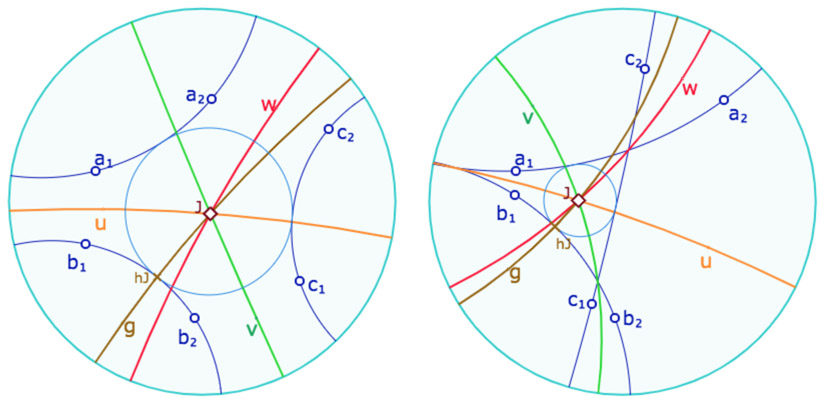
Le théorème ne nécessite pas d’hypothèses sur les droites \(a, b, c\). Voici deux illustrations
On a ajouté le cercle inscrit du trilatère … qui devient un triangle à droite.
Lancer cette figure dans un nouvel onglet
Du point de vue de la géométrie dynamique, cette figure n’est pas aussi triviale qu’il y paraît car quand les droites se coupent (comme à droite) il faut traiter la continuité de la bissectrice … pour qu’elle reste la bissectrice intérieure. Ce point délicat (y compris théoriquement) a déjà été abordé dans cette page du menu DP.
Quand les bissectrices ne sont pas en pinceau
Cela ne concerne que la géométrie hyperbolique car dans le cas elliptique, deux droites étant sécantes, le point \(J\) du théorème 21a existe toujours. Dans le cas hyperbolique, quand ce point d’intersection n’existe pas, il peut ne pas y avoir de pinceau de bissectrices.
Il existe néanmoins des points bissecteurs. Bachmann garde le terme de « milieu » de deux droites (Mittelpunk dans le Aufbau de 1959 p 52). Daniel Perrin, lui, utilise le terme de bissecteur. Voici une propriété des bissecteurs mais qui n’est pas montré par Bachmann qui n’utilise finalement pas les bissecteurs.
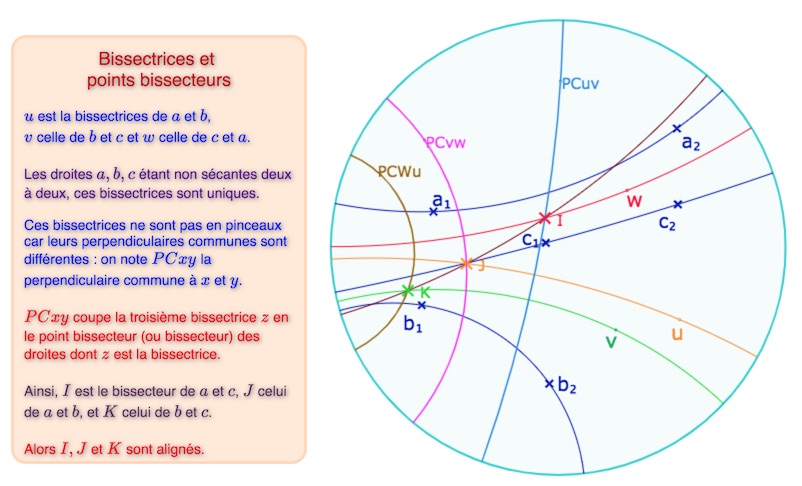
Lancer cette figure dans un nouvel onglet. Conserver les droites \(a, b, c\) non sécantes.
Un mot sur l’approche KE-KH
Sur ce thème (comme sur d’autres) l’approche – très différente – de Daniel Perrin, parce qu’elle est projective, est plus efficace. Dans les articles de ce site à propos de cette approche, on appelle KH le plongement projectif du plan hyperbolique. Comme on dispose de la polarité, les bissectrices de trois droites sont les médiatrices de leurs pôles et donc les bissecteurs, les milieux des pôles. Dans ce contexte projectif, chaque point a deux milieux, il y a donc deux bissecteurs pour deux droites (un à l’extérieur du cercle horizon bien entendu). Il y a alors, « naturellement » peut-on dire, quatre droites d’alignement des points bissecteurs pris par trois. La démonstration est p. 104 de ce fichier souvent mentionné DPPartie4.
Signalons que KH n’est pas une géométrie de Bachmann essentiellement parce que l’axiome d’incidence n’est pas respecté. Pour rappel, Daniel Perrin s’en explique ainsi :
Attention, par rapport aux textes standards sur les géométries non euclidiennes, ce livre présente une singularité. En effet, les points et les droites que nous définissons ici ne vérifient pas toujours l’axiome de base de la géométrie d’Euclide : par deux points passe une droite et une seule. Il nous semble, en effet, qu’il est préférable de renoncer à cet axiome dans un premier temps, même si le poids des traditions s’y oppose. Cette généralisation ne concerne d’ailleurs que le cas hyperbolique pour lequel elle revient à ajouter aux points du disque de Klein les points extérieurs. Dans ce cas, on verra que le surcroît d’efficacité obtenu en utilisant la polarité vaut bien quelques concessions. On verra tout au long des chapitres suivants qu’on retrouve aisément les résultats usuels en spécialisant les résultats généraux aux points et droites hyperboliques.
Daniel Perrin – Partie 4 – pages 22-23
Retour à la présentation de Bachmann
Il propose ensuite un énoncé plus général, grâce en particulier aux théorèmes de transitivité de la relation « être en pinceau ».
Th 21b : bissectrices en pinceau
Soient \(a, b, c\) trois droites non en pinceau, et \(u\) et \(w\) deux droites telles que \(c^u=b\) et \(b^w=a\). Alors :
S’il existe une droite \(v\) à la fois en pinceau, avec \(a\) et \(c\) d’une part et avec \(u\) et \(w\) d’autre part, alors \(c^v=a\).
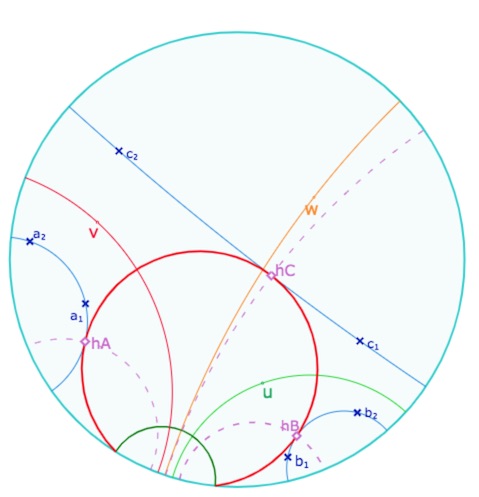
Illustration de la démonstration dans le cas de pinceau à axe,
avec les pieds \(h_B, h_C, h_A\) respectivement sur \(b, c, a\).
On a donc \(b^w=a\) et \(b^u=c\). Puisque \(v \in \mathscr{P}_{ac}, \; cva = b^uvb^w\) est une droite. de même, comme \(v \in \mathscr{P}_{uw}, \; uvw\) est aussi une droite. \(b^u=c\) s’écrit aussi \(ub=cu\), et de même \(b^w=a\) s’écrit aussi \(wb=aw\). Alors \(u(cva)w\) s’écrit aussi \(bu.v.wb\) soit \((uvw)^b\) et donc est une droite, et même (revoir le th 16) de \(\mathscr{P}_{uw}\).
Cela signifie aussi que \(b^uvb^w \in \mathscr{P}_{uw}\), et donc, au final, les deux droites \(v\) et \(b^uvb^w\) sont deux droites qui appartiennent aux deux pinceaux \(\mathscr{P}_{uw}\) et \(\mathscr{P}_{ac}\).
Pour montrer que \(v=b^uvb^w\), il suffit de montrer que les deux ponceaux sont distincts (car par le th 18 il n’existe au plus qu’une droite à l’intersection de deux pinceaux).
Pour cela, montrons que \(b^u \notin \mathscr{P}_{uw}\). En effet, si \(b^u\) tait dans ce ponceau, le produit \(b^uuw=ubw\) serait une droite – et en particulier égal à son inverse. Alors \(cba = b^ubb^w = (ub)ubw(bw) = (ub)wbu(bw) = (wbu)b(ubw)=b^{ubw}\) dont serait une droite, ce qui n’est pas car, par hypothèse du théorème, \(a, b, c\) ne sont pas en pinceau.
Et donc les deux pinceaux étant distincts, leur intersection, si elle existe, est unique (th 18), et donc \(v=b^uvb^w=cva\), soit \(c^v=a\). De plus, on a \(uvw=u(b^uvb^w)w=(uvw)^b\). Comme \(uvw \neq b\) (car sinon \(ubw\) seraient une droite) et qu’elle est stable par \(b\), alors nécessairement \(uvw \perp b\).
Cela donne la perpendiculaire aux droites \(a, b, c\) appartenant au pinceau des bissectrices simplement par le produit de ces droites, donc les points de contact des cycles exinscrits par exemple, ceci indépendamment de la nature du cycle exinscrit (cercle, horicycle ou équidistante). C’est ainsi que sont construits les points \(h_A, h_B, h_C\) dans l’illustration précédente.
Lancer cette figure dans un nouvel onglet.
Compléments sur les propriétés du cercle inscrit et des cycles exinscrits dans cet article.
Les théorèmes des milieux
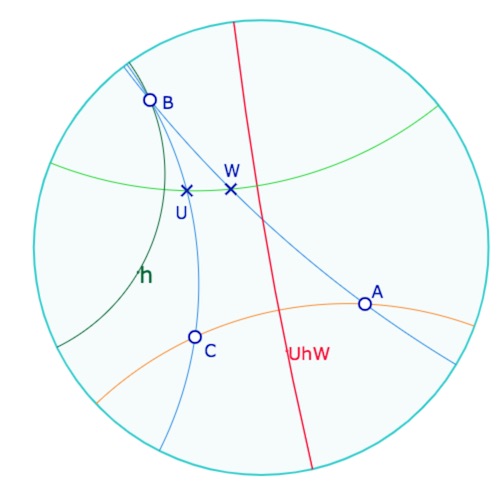
Th 22 : le théorème des milieux
Soit \(ABC\) un triangle. S’il existe deux points \(U\) et \(W\) tels que \(C^U=B\) et \(B^W=A\) alors il existe une droite \(v\) telle que \(UvW\) soit une droite et tel que \(C^v=A\).
La droite passant par deux milieux de deux « côtés » d’un triangle et le troisième « côté » de ce triangle ont pour perpendiculaire commune une médiatrice de ce troisième côté.
Le terme « côté » est un abus langagier simplificateur car on ne peut pas définir de notion de segment à ce stade de la théorie, on n’a besoin que des centres de symétrie de sommets en réalité. Par « triangle » on entend « trois droites deux à deux sécantes ».
Preuve : soit \(h\) une* perpendiculaire à la droite \((UV)\) issue de \(B\). Par le théorème 10 (la version algébrique de Hjelmselv), on sait que \(UhW\) est une droite \(v\), et on a \(C^v= C^{UhW} =B^{hW}= B^W=A\).
Lancer la figure de l’illustration hyperbolique dans un nouvel onglet.
(*) : on n’a besoin que de l’existence d’une perpendiculaire. Mais, par ailleurs, si \(B\) devait être le pôle de \((UW)\), les points \(B\) et \(C\) seraient confondus, ce qui n’est pas le cas car on parle de vrai triangle \(ABC\). Donc dans tous les cas, il s’agit de la perpendiculaire.
« une médiatrice » car dans le cas elliptique, il existe deux milieux \(U\) et \(W\) donc plusieurs droites latex]h[/latex] et ainsi plusieurs possibilités pour la droite latex]v[/latex] . En réalité, comme dans le théorème 20, deux seulement, même s’il y a quatre droites \(h\).
Dans l’illustration suivante, les droites \(h\), notées \(h_{xy}\) sont indexées en \(U, V\), ainsi \(h_{ie}\) est la perpendiculaire à \((U_{int}W_{ext})\) passant par \(B\).
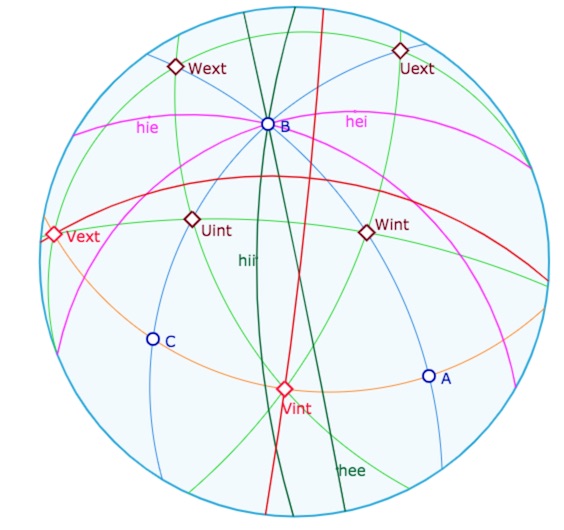
Illustration de la preuve précédente dans le contexte elliptique
En utilisant la polarité, il est facile de repérer quelle médiatrice (droite rouge) passant par \(V_{int}\) ou \(V_{ext}\) est produit de \(W_{xy}h_{xy}U_{xy}\). Pour cela on repère par quel troisième milieu passe la droite \((W_{xy}U_{xy})\). En effet comme la perpendiculaire commune de deux droites est la polaire de leur intersection, il est clair que la médiatrice passant par \(V_{int}\) est issue des deux hauteurs \(h_{ii}\) et \(h_{ee}\) : elle est la polaire de \(V_{ext}\), et donc la perpendiculaire commune de \((AB)\) et de \((U_{int}W_{int})\), mais aussi de \((AB)\) et de \((U_{ext}W_{ext})\). Et la médiatrice issue de \(V_{ext}\) provient des deux autres hauteurs \(h_{ie}\) et \(h_{ei}\).
Lancer la figure de cette illustration elliptique dans un nouvel onglet.
Th 23 : réciproque du théorème des milieux
Soit \(ABC\) un triangle. S’il existe une droite \(u\) et un point \(W\) tels que \(C^u=B\) et \(B^W=A\) alors il existe un point \(V\) tel que \(uVW\) soit une droite et \(C^V=A\).
La perpendiculaire à une médiatrice d’un côté d’un triangle passant par un milieu d’un autre côté coupe le troisième côté en un milieu. (avec les remarques précédentes sur l’expression « côté »)
Preuve : soit \(s\) une perpendiculaire à \(u\) issue de \(W\) et \(h\) une perpendiculaire à \(s\) issue de \(B\). Alors, par le théorème 10, \(uWh\) est un point \(P\), et donc \(uhW=uhu(uWh)h=h^uPh\) est un point \(V \; (\in s)\) vérifiant \(C^V=C^{uhW}=B^{hW}=B^W=A\).
Enfin \(uVW=u(uhW)W\) est bien une droite, puisque ce n’est autre que la droite \(h\).
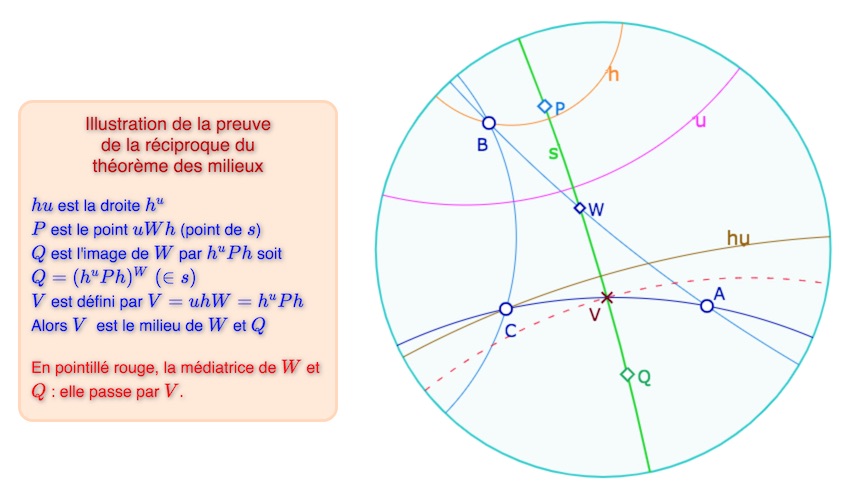
Lancer cette figure dans un nouvel onglet.
Les hauteurs d’un trilatère
Th 24 : hauteurs d’un trilatère
Soit \(a, b, c\) un trilatère non tripolaire (\(abc \neq 1\)) et \(u, v, w\) telles que
i) \(u \perp a, v \perp b\) et \(w \perp c\).
ii) \(ubc, avc\) et \(abw\) sont des droites.
Alors \(uvw\) est une droite (ie les trois droites sont en pinceau).
Remarque sur l’écriture du théorème : la seconde série d’hypothèses sur \(u, v, w\) est celle de l’existence d’une droite appartenant à l’intersection du pinceau formé de deux droites et de celui des droites orthogonales à la troisième. On a vu (Th 18) que l’intersection de deux pinceaux contient au plus une droite : les existences de \(u, v, w\) ainsi définies ne sont pas certaines a priori, elles sont donc dans les hypothèses du théorème. Par exemple dans le cas elliptique, l’écriture du théorème pourrait être différente car deux droites sont toujours sécantes.
Le théorème dit tout simplement que, quand elles existent toutes les trois, les hauteurs d’un trilatère sont toujours en pinceau. C’est en particulier le cas pour les triangles.
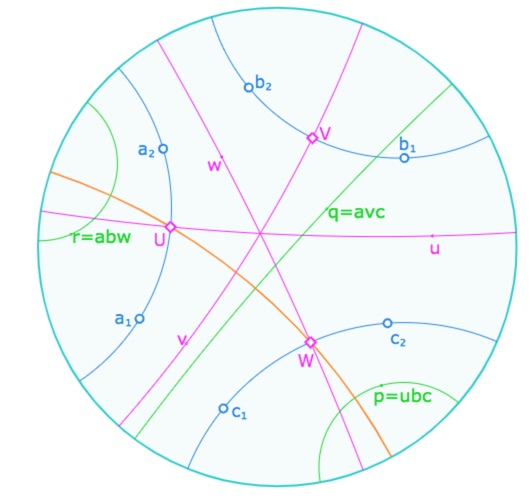
On note \(U=au=ua, V=vb=bv, W=wc=cw\) es pieds des hauteurs et \(p=ubc, q=avc\) et \(r=abw\). On a rapidement les relations \(Up=abc\), et donc \(Up=qV^c\) et \(Up=rW\).
De même, puisque \(q=avc=cva \)car une droite est égale à son inverse, on peut écrire\(pqr=(ubc)(cva)(abw) =ubvbw=uv^bw=uvw\) car \(v^b=v\) puisque \(v \perp b\). Soit \(pqr=uvw\).
Pour montrer que \(uvw\) est une droite, on va montrer que \(pqr\) en est une, et plus précisément que ces trois droites sont en pinceau à axe, d’axe la droite \((UW)\), c’est-à-dire que \(p, q, r\) sont toutes les trois orthogonales à \((UW)\).
• De \(Up=abc \neq 1\) et du Th 4 (unicité de la perpendiculaire hors polarité) , il existe une unique droite \(h\) perpendiculaire à \(p\) issue de \(U \; : \; h \mid p, U\).
• De \(Up=qV^c\), on en déduit que \(qUp=V^c\) est un point. Et donc, par le théorème 11, on sait que \(qUp\) est un point si et seulement si il existe une droite \(g\) telle que \(g \mid p, q, U\), et donc \(g\) est la perpendiculaire commune à \(p\) et \(q\) passant par \(U\). Par unicité de la droite \(h\), on a \(g=h\). Et donc \(h\) est orthogonale à \(p\) et \(q\).
• Enfin la troisième relation \(Up=rW\) s’écrit d’une part \(rUp=W\), et donc \(rUp\) est un point et donc \(h\) est aussi orthogonale à \(r\).
D’autre part \(Up=rW\) s’écrit aussi \(U=rWp\) et, toujours par le Th 11, on en déduit que la perpendiculaire commune à \(r\) et \(p\) passe aussi par \(W\). Et donc la droite \(h\) passe aussi par \(W\).
En définitive \(h=(UW)\) et \(p, q, r \mid h\). Donc, par l’axiome A4, \(pqr \)est une droite, et par le complément à l’axiome A4, c’est une droite orthogonale à \((UW)\).
Lancer la figure associée à cette preuve dans un nouvel onglet.
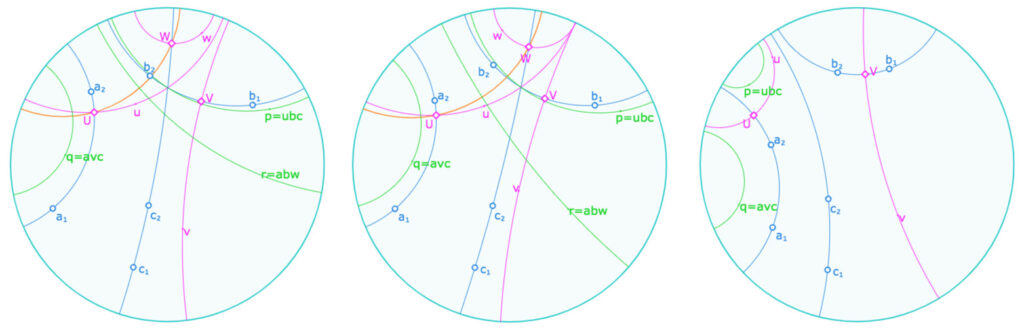
Trois illustration sur le pinceau des hauteurs d’un trilatère
à gauche les hauteurs sont en pinceau « à axe » (non construit), au centre il est « sans support » (les trois hauteurs sont parallèles), à droite il n’existe que deux hauteurs.
Th 25 : bissectrices du triangle podaire
Le pinceau des hauteurs d’un trilatère est aussi le pinceau des bissectrices de son triangle podaire.
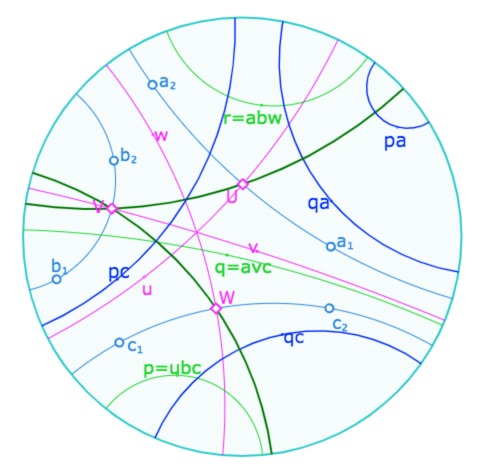
Preuve : le principe est de montrer que le symétrique de la droite \((VU)\) par rapport à la droite \(v\)est la droite latex](VW)[/latex]. Mais pour le moment on ne connait essentiellement qu’une propriété de la symétrie orthogonale : elle conserve l’orthogonalité. Donc on va montrer qu’une perpendiculaire à \((VU)\) est perpendiculaire à \((VW)\). On va ainsi être amené à montrer que \((VU)\perp q^a\) et que \((VW)\perp q^c\).
On utilise la même démarche que ci-dessus. On ira un peu plus vite.
Dans l’illustration ci-contre, les droites nommées \(pc, qp, pa, qa\) sont les droites \(p^c, q^p, p^a, q^a \) de la preuve.
On a \(q^c = cav, p^c = cub=buc\). Et donc avec \(V=bv=vb\), il vient \(q^cVp^c = caua = U^c\). Ainsi \(q^cVp^c\) est un point. Cela signifie (Th 11) que la perpendiculaire commune à \(q^c\) et à \(p^c\) passe par le point \(V\). Comme on vient de montrer au théorème précédent que les droites \(p\) et \(q\) ont la droite \((UW)\) comme perpendiculaire commune, les droites \(p^c\) et \(q^c\) ont la droite \((U^cW^c)\) comme perpendiculaire commune et donc \(W \; (=W^c)\) est sur la perpendiculaire commune à \(p^c\) et \(q^c\) : cette perpendiculaire commune est donc la droite \((VW)\).
De même, la perpendiculaire commune à \(p^a\) et \(q^a\) passe par \(U^a=U\). montrons qu’elle passe aussi par \(V\). Pour cela il faut montrer que \(p^aVq^a\) est un point. De \(p=ubc=cbu\), on a \(p^a\)=acbua, et de \(q=avc\), on a \(q^a=vca\). On insère \(V=bv=vb\), ce qui donne \(p^aVq^a=(acbua)(bv)(vca) =(acb)ua(bca)=U^{bca}\). C’est donc un point. Ainsi la perpendiculaire commune à \(p^a\) et \(q^a\) est la droite \((VU)\).
Comme indiqué en préambule de la preuve, pour montrer que \((VU)^v=(VW)\), on va montrer que c’est le cas des droites orthogonales , à savoir que \((q^a)^v=q^c\). Or c’est immédiat (maintenant … tout a été préparé pour ….). En effet \((q^a)^v=v((vca)v=cav=q^c\). Ce qui achève le fait que les hauteurs d’un trilatère sont les bissectrices de son triangle orthique.
Lancer la figure de cette preuve dans un nouvel onglet.
On rappelle qu’en déplaçant les poignées des droites (les points \(a_1, a_2, b_1, b_2, c_1, c_2\)), les noms de toutes les droites vont aller vers le cercle horizon. Il suffit de se rapprocher d’eux et les déplacer quand ils sont surlignés.
Le cycle inscrit ou exinscrit associé aux hauteurs
Dans l’illustration suivante, on voit que l’orthocentre peut être le centre d’un cercle inscrit ou exinscrit au trilatère. Et quand le pinceau devient à axe le cercle devient une équidistante. On remarquera que l’on utilise le même point (nommé \(Pt\)) du point de contact du cycle sur la droite \((UV)\), obtenu par le principe détaillé en fin du th 21b ci-dessus.
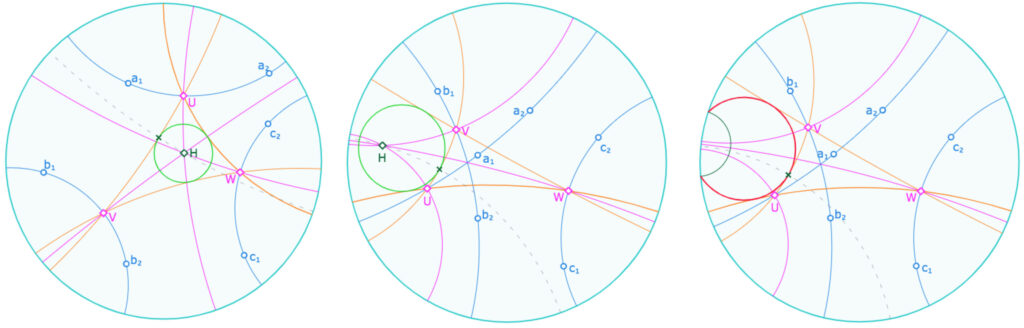
Figure dynamique associée
Cette figure contient aussi une situation non prise en compte dans ce théorème, le cas où un des pieds des hauteurs est -potentiellement – un point à l’infini (traité seulement pour le point \(U\) comme illustration) et donc quand une hauteur n’existe pas. Alors le cycle exinscrit au triangle orthique (nécessairement idéal) est l’équidistante elle-même.
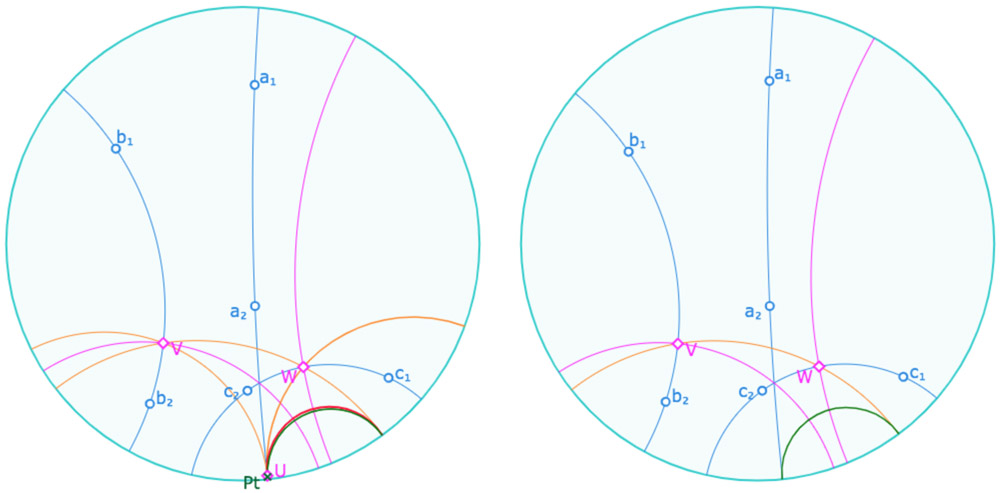
Dans l’illustration de gauche, le point \(U\) est « presque » un point idéal, mais il existe, et on voit l’équidistante rouge proche de la perpendiculaire commune.
Dans l’illustration de droite, on a juste déplacé le point \(b_1\) de quelques pixels, alors le point \(U\) devient un point idéal (ici qui a disparu).
On pourrait chercher à affiner la figure pour que le triangle orthique (idéal) continue d’exister.
Une conséquence de cet ajout est que, dans la manipulation de la figure, on peut voir apparaître parfois la perpendiculaire commune à deux hauteurs.
Préférer lancer cette figure dans un nouvel onglet.
Complément : l’isogonal de l’orthocentre
De par les définitions de \(p, q, r\), on a les relations d’isogonalité \(pc=ub, qc=av\) et \(ar=bw\). On peut alors écrire \(q.p^c.r^a =q.cub.bwa=avuwa =(vuw)^a\).
Donc les trois droites \(q, p^c, r^a\) sont en pinceau : c’est le pinceau isogonal du pinceau des hauteurs.
On notera que le pinceau isogonal d’un pinceau n’est pas nécessairement de même type. Ainsi on peut avoir les hauteurs concourantes, et le pinceau isogonal à axe comme dans l’illustration de droite.
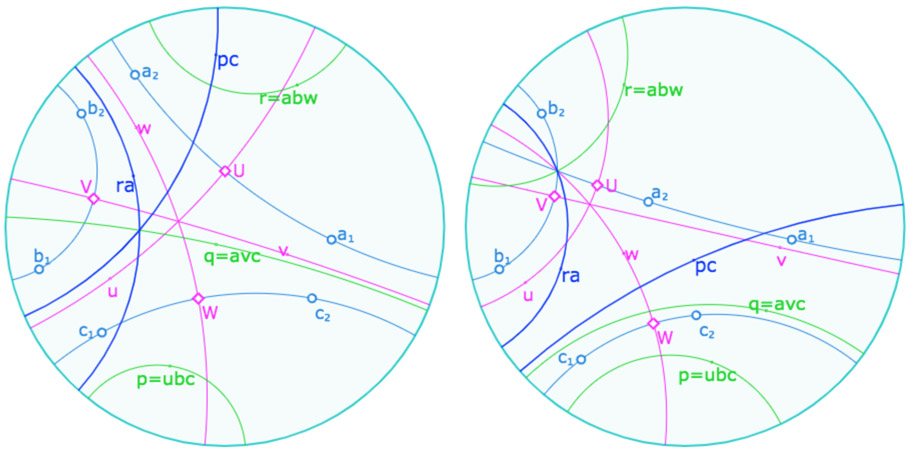
Les droites nommées \(pc\) et \(ra\) sont les droites \(p^c, r^a\).
à gauche : l’isogonal d’un pinceau à centre est à centre, à droite c’est un pinceau à axe.
De même, le résultat euclidien sur l’isogonal de l’orthocentre d’un triangle, à savoir « l’isogonal de l’orthocentre est le centre du cercle circonscrit » n’est pas une propriété absolue.
Lancer la figure précédente sur le pinceau isogonal dans un nouvel onglet.
Isogonalité de pinceaux
Th 26 : isogonalité
Soient \(a, b, c, p, q, r\) et \(u, v, w\) des droites telles que \(u=bpc, v=cqa\) et \(w=arb\). Alors si \(p, q, r\) sont en pinceau, \(u, v, w\) le sont aussi.
Preuve : si \(pqr\) est une droite, alors on peut écrire \(uvw=(bpc)(cqa)(arb) = b(pqr)a=(pqr)^a\) donc est une droite, donc \(u, v, w\) sont bien en pinceau.
Dans la figure proposées ci-dessous, les droites \(a, b, c \) sont pilotées par deux poignées chacune, mais les droites \(p, q, r\) ne sont pilotées que par une seule poignée, les points \(p_1, q_1, r_1\). Le point \(r_1\) est de plus aimanté par l’intersection des pinceaux \(\mathcal{P}_{ab}\) et \(\mathcal{P}_{pq}\) pour réaliser les illustrations de droite : \(p, q, r\) sont en pinceau, et donc \(u, v, w\) aussi. Quand elles sont en pinceau à axe, la perpendiculaire commue à \(u\) et \(v\), \(PCuv\) d’une part et celle commune à \(v\) et \(w\), la droite \(PCvw\) d’autre part, coïncident. C’est le cas à droite, et pas à gauche, quand les droites \(p, q, r\) ne sont pas en pinceau.
Les illustrations suivante montrent trois cas de type de pinceau possibles, à gauche dans le cas général, à droite quand on rend \(p, q.r\) en pinceau (par aimantation).
• En haut, les droites \(p, q, r\) sont à centre, et \(u, v, w\) sont à axe.
• Au centre, les deux sont à axe.
• En bas, les deux sont à axe.
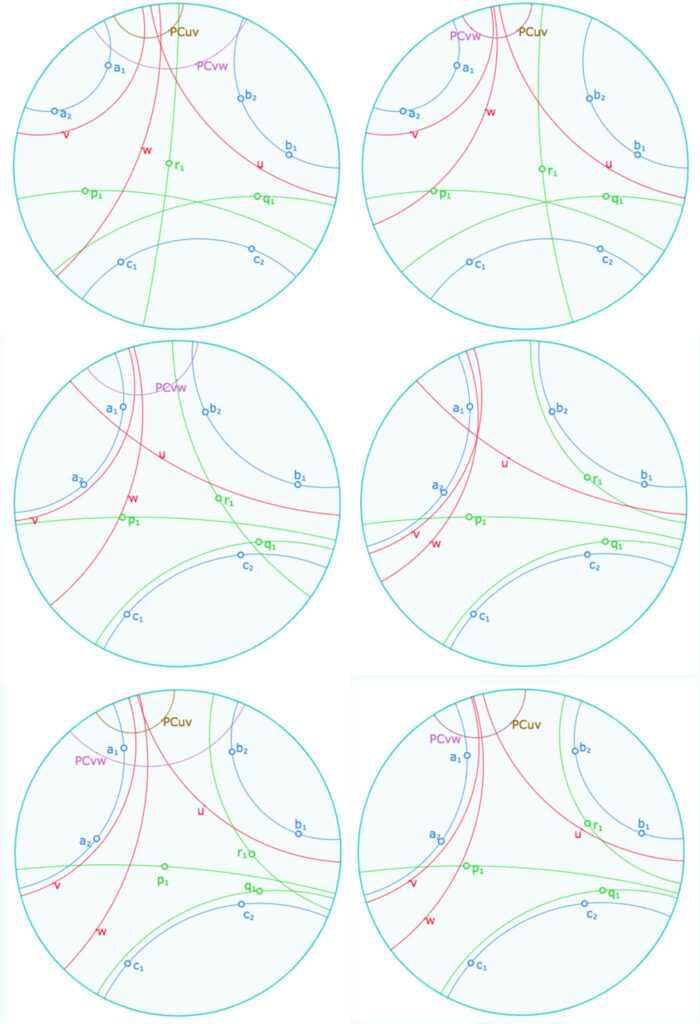
Exemple de situations que l’on peut réaliser avec la figure suivante.
Figure d’isogonalité absolue
Penser aussi à déplacer toutes les poignées des droites. On rend \(p, q.r\) en pinceau en déplaçant le point \(r_1\).
Préférer ouvrir cette figure dans un nouvel onglet.
Cas du triangle
On retrouve (presque) le contexte euclidien
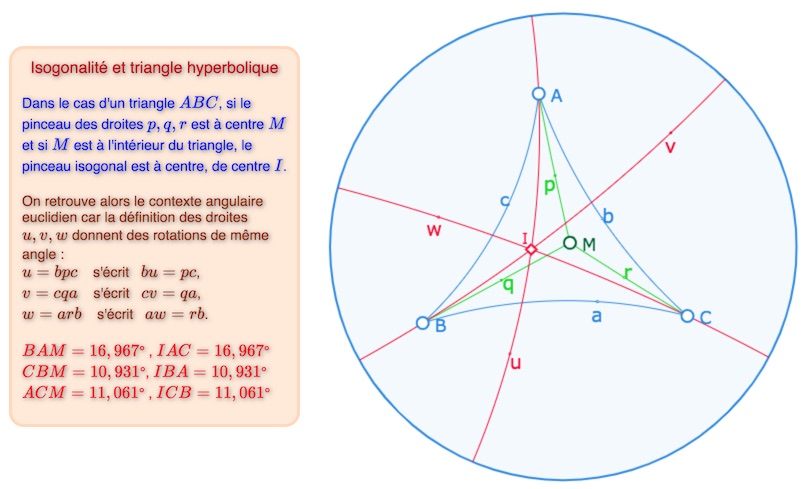
Ouvrir cette figure dans un nouvel onglet
Rappel de manipulation : en déplaçant par exemple le point \(M\), les noms des droites \(p, q, r\) peuvent tous les trois se retrouver en latex]M[/latex] ou parfois l’un d’eux en un sommet du triangle. De même les noms des droites \(u, v, w\) peuvent se retrouver sur l’horizon. On les déplace simplement en les prenant à la souris.
… contexte presque euclidien … car quand \(M\) sort du triangle, le pinceau peut être encore à centre, ou pas.
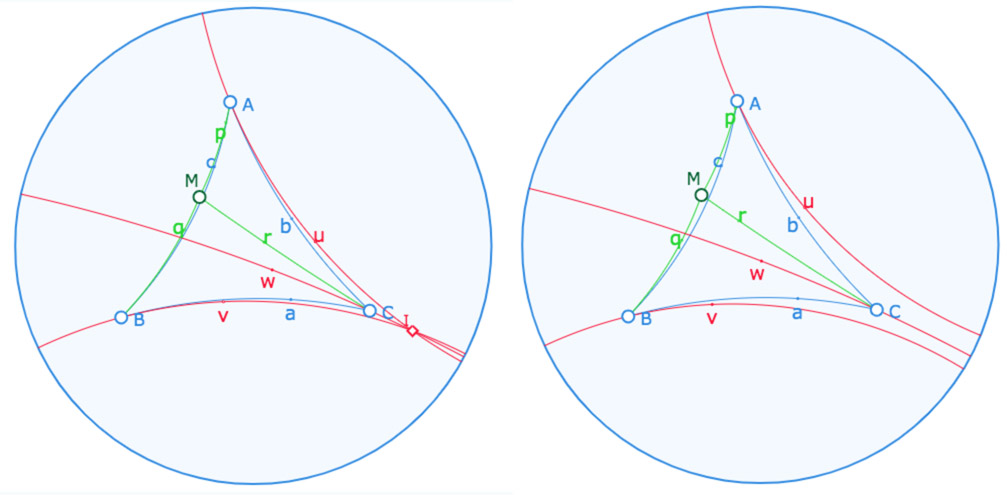
Exercice (pour de futurs posts de blog) : peut-on caractériser le lieu des points \(M\),
pour un triangle donné, tel que le point \(I\) soit un point idéal ?