Quand on manipule la figure générale des hauteurs d’un triangle de la page précédente, on observe que souvent, hors des cas que l’on a dit «géométriques», les hauteurs ne deviennent concourantes que si le triangle devient rectangle. Néanmoins, on rencontre aussi des situations où l’on arrive à produire, empiriquement – et très localement – quelques triangles orthocentriques. C’est ce que l’on se propose d’étudier ici.
Équation des hauteurs
Pour commencer, précisons les différentes écritures des (parties) des hauteurs d’un triangle de Moulton. On se donne un point \(A\) et une droite \((BC)\). L’équation de la perpendiculaire à \((BC)\) passant par \(A\), ou une partie de la hauteur – selon les demi-plans délimités par l’axe des ordonnées – est de l’une des deux formes :
\((Eq_1) \quad y= \displaystyle k\frac{x_c-x_B}{y_B-y_C}(cx-x_A)+y_A\) ou \((Eq_2) \quad y= \displaystyle k\frac{2x_c-x_B}{y_B-y_C}(x-x_A)+y_A\)
où \(k\) et \(c\) prennent les valeurs \(\frac{1}{2}, 1, 2\)
Pour une droite à pente positive, une perpendiculaire est à pente négative, il y a deux écritures algébriques selon le demi-plan. En pratique, il y a 7 écritures formelles différentes de type \((Eq_1)\). Le cas des droites à pente négative ajoute la seconde écriture \((Eq_2)\), non symétrique en \(B\) et \(C\) dans le cas où \(B\) à abscisse négative et \(C\) à abscisse positive.
Au final, on aboutit à 9 expressions possibles pour les hauteurs, et donc 81 écritures différentes de l’intersection de deux hauteurs. L’objectif de cette section n’est pas l’étude exhaustive de toutes ces possibilités, d’autant que l’on s’intéresse à trois hauteurs.
Mais surtout, la géométrie dynamique permet de repérer rapidement les configurations produisant des résultats intéressants. On se propose donc de repérer ces configurations, puis de les étudier algébriquement et produire les figures dynamiques associées.
Triangles orthocentriques à trois pentes négatives
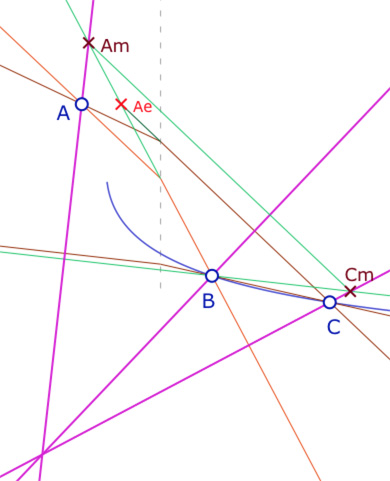
En terme d’expression des hauteurs, le cas le plus simple à traiter est celui d’un triangle ayant ses trois côtés à pentes négatives car les trois hauteurs sont alors des droites à pentes positives, donc des droites euclidiennes. Comme transition avec le cas « géométrique » de la page précédente, nous allons conserver dans un premier temps un regard géométrique. Nous verrons toutefois que celui-ci perd rapidement de sa pertinence.
Une première approche, partiellement géométrique

Dans la figure que l’on étudie ici, le triangle est à trois pentes négatives, avec \(x_A < 0, \, x_C > x_B >0\). Les hauteurs issues de \(B\) et \(C\) sont orthogonales à la partie positive du côté opposé et celle issue de \(A\) à la partie négative de son côté opposé. L’orthocentre cherché est alors à abscisse négative.
L’approche géométrique consiste à chercher un triangle \(A_mBC_m\) pour lequel les trois hauteurs du triangle de Moulton \(ABC\) – qui sont des droites euclidiennes – soit aussi les hauteurs euclidiennes de ce triangle.La parallèle passant par \(B\) à la partie négative de la M-droite \((BC)\) coupe la hauteur de \(ABC\) issue de \(C\) en \(C_m\).
La droite euclidienne support de partie positive de la M-droite \((AB)\) coupe la hauteur de \(ABC\) issue de \(A\) en\(A_m\). Le point \(A_e\) (à demi-abscisse de \(A\)) est sur le côté \([BA_m]\) de \(A_mBC_m\) et sur le support de la partie positive de la M-droite \((AC)\). Alors, par construction du triangle \(A_mBC_m\) son orthocentre euclidien est aussi celui du triangle de Moulton \(ABC\) si et seulement si \((A_eC) // (A_mC_m)\).
On cherche donc les pentes de ces deux droites et on se propose de chercher le lieu du point \(B\) (avec la contrainte initiale \(x_C > x_B >0\)) qui réalise l’égalité de ces deux expressions.
La pente de \((A_eC)\) est \(\displaystyle \frac{2(y_A-y_C)}{(x_A-2x_C)}\).
En notant \(B(x,y)\), dans le cadre des contrainte de la figure étudiée, la pente de la droite \((A_mC_m)\) est :
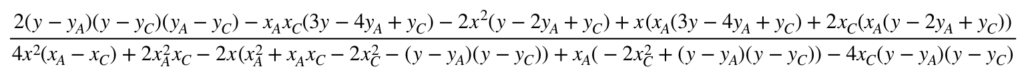
En égalant les deux pentes, on obtient le résultat suivant que l’on présente dans un contexte plus général applicable à tous les calculs effectués sur cette page.
Compte tenu des écritures générales des hauteurs et des droites de Moulton, très similaires (à un coefficient \(k\) près prenant trois valeurs), tout ce que l’on va étudier dans la suite s’inscrit dans un résultat général où les lieux solutions seront de ces seules deux formes :
\(Type \; (1) \quad y = \displaystyle \frac{a(x)-\sqrt{a(x)^2-2d(x)c(x)}}{d(x)} \;\) ou \(\; Type \; (2) \quad y = \displaystyle \frac{a(x)+\sqrt{a(x)^2-2d(x)c(x)}}{d(x)}\)
En posant \(a(x)=(x_A-2x_C)(3x_A-2x)+4(y_A^2-y_C^2), \quad d(x) = 8(y_A-y_C)\) – ici \(d\) est fixe, et
\(c(x) = 4x_Ay_A(x-x_C)+y_C(3x_A-2x_C)(x_A-2x)+y_Ay_C(y_A-y_C)\).
Alors \(B(x,y)\) réalise un triangle orthocentrique de Moulton \(ABC\) pour l’écriture de Type (1) ci-dessus, avec la contrainte initiale de la figure \(x_C > x_B >0\).
Dans la figure suivante, on peut agir sur les points de base, y compris \(B\) qui est aimanté par le lieu solution – en bleu dans l’illustration – ce qui permet d’explorer les cas solutions (\(B\) sur le lieu) et les cas non solution, quand les droites \((A_eC)\) et \((A_mC_m)\) ne sont pas parallèles.
Premier exemple de triangle orthocentrique «algébrique». \(B\) à abscisse positive.
Déplacer les points \(A, B\) ou \(C\), en respectant les contraintes pour lesquelles la figure a été calculée.
Préférer ouvrir la figure dans un nouvel onglet
Cette approche géométrique a été proposée pour montrer qu’on peut chercher un triangle euclidien pour lequel les orthocentres euclidien et de Moulton vont coïncider avec une condition géométrique particulière à résoudre. Mais compte tenu de l’expression de la pente de \((A_mC_m)\) calculée plus haut, on voit qu’il peut être tout aussi efficace de chercher les coordonnées des intersections des M-hauteurs prises deux à deux et de les égaliser. Nous allons même voir que dans certains cas, de vraies surprises de simplification nous attendent.
Traversée de l’axe des ordonnées par le point \(B\)
On poursuit sur la même configuration de trois droites à pentes négatives, mais en plaçant \(B\) à gauche de l’axe des ordonnées, soit \(x_A < x_B <0\) et \(x_C >0\), avec les contraintes associées sur les ordonnées. Les hauteurs issues de \(B\) et \(C\) sont à nouveau orthogonales à la partie positive de leur côté opposé respectif, et celle issue de \(A\) à la partie négative de son côté opposé \((BC)\). Mais les équations changent et les résultats sont sensiblement différents.
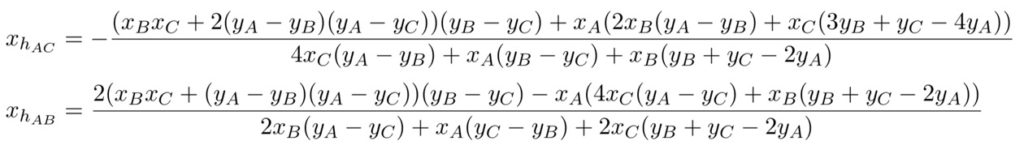
On commence par calculer les abscisses des intersections \(h_{AB}\) et \(h_{AC}\) des hauteurs issues de \(A\) et \(B\) d’une part et celles issues de \(A\) et \(C\) d’autre part.
En égalisant ces deux abscisses, on a une relation entre les coordonnées des trois points. On peut chercher celles d’un point en fonction des quatre autres. Commençons, dans la continuité de ce qui précède, par \(B\) en fonction de \(A\) et \(C\). \(B(x, y)\) est alors solution d’une relation de Type (2) avec :
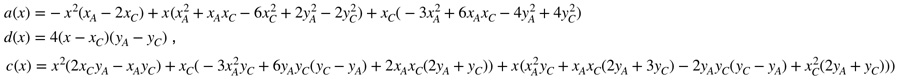

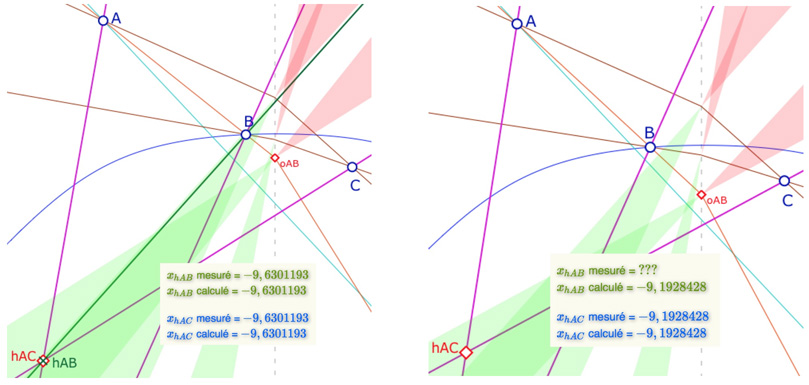
Sur l’illustration on a laissé le lieu des points \(B(x, y)\) mais les contraintes de la figure limitent, sur cette courbe, à ne prendre \(B\) qu’entre l’axe des ordonnées et la droite issue de \(AB\), en bleu sur la figure, qui est telle que le point \(o_{AB}\)est sur la hauteur issue de \(C\), donc position limite pour que la hauteur soit prise sur la partie positive de la M-droite \((AB)\). La limite de la pente de la droite \((AB)\) est donnée par \(p_{AB} min = \displaystyle \frac{y_A-y_C+\sqrt{(y_A-y_C)^2-2x_Ax_C}}{2x_A}\).
Ainsi \(B\) est limité à être, sur la courbe, entre cette droite et l’axe des ordonnées.
Avant de proposer cette figure à la manipulation, signalons d’autres contraintes assez spécifiques qui n’apparaissent pas sur l’illustration ci-contre. Il s’agit du cas où la courbe rencontre la zone verte \(pdp_{AC}\) avant la droite à pente minimale. Alors la partie de la courbe avant la droite bleue et après la zone verte n’est pas solution pour le point \(B\) tout simplement parce que la perpendiculaire à la partie droite de la M-droite \((AC)\) n’existe pas.
Dans les illustrations suivantes, à gauche, le cas ordinaire où il y a un orthocentre. Á droite, \(B\) étant en dehors de \(pdp_{AC}\), il n’y a pas de perpendiculaire à la partie positive de la droite \((AC)\). On remarque pourtant que le calcul de \(x_{hAB}\) est encore effectué, et qu’il donne le bon résultat. En effet, le calcul est algébrique et est effectué dans le logiciel, comme indiqué par les formules, indépendamment de l’existence effective des M-perpendiculaires. Il n’y a donc pas d’incohérence, juste un calcul algébrique permanent. La partie mesurée, elle, n’existe pas, car il n’y a pas de perpendiculaire réelle.
Manipulation de la figure « lieu de B »
En déplaçant \(C\) lentement, \(B\) reste sur la courbe, sinon, on peut remettre facilement \(B\) sur la courbe. On peut explorer en détail les différente situations exposées.
Préférer ouvrir la figure dans un nouvel onglet
Clairement, le lieu de \(B\) est assez limité et très contraint. Même si c’est mathématiquement équivalent, d’un point de vue de la dynamique des figures, il est plus intéressant, dans l’égalité \(x_{hAB}=x_{hAC}\), de chercher le lieu des points \(C\) en fonction de \(A\) et \(B\) . On trouve alors les valeurs suivantes, pour une formule de Type (1) :
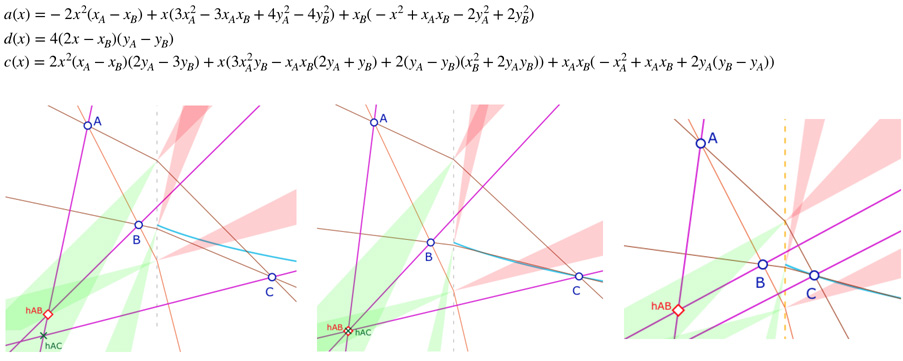
à gauche : \(C\) n’est pas sur la courbe, pas d’orthocentre. Au centre : \(C\) est sur la courbe, les deux points sont confondus,, il y a orthocentre.
à droite : il y a une nouvelle contrainte, \(C\) doit être en dessous de \(psp_{AB}\) sinon la hauteur issue de \(C\) coupe la partie négative de la droite \((AB)\) alors que les calculs ont été faits pour la partie positive.
Comme pour les autres figures, on peut décoller \(C\) de la courbe.
En déplaçant lentement \(A\) ou \(A\) , \(C\) reste collé à la courbe solution.
Préférer ouvrir la figure dans un nouvel onglet
Triangles orthocentriques à une seule pente de Moulton négative
Comme on a vu, à la page précédente, que le cas à deux pentes négatives se traite simplement par des arguments géométriques, il reste à étudier le cas où un triangle a une seule pente de Moulton négative. Ce sera la droite \((AB)\). Pour les calculs, on se fixe \(x_A<0\) et \(x_B>0\).
Il y a alors deux configurations génériques possibles : soit \(y_C>y_A\), soit \(y_C<y_B\), ce dernier cas étant très riche car il contient des situations à cinq hauteurs.
Dans chacune de ces deux situations, on peut chercher un orthocentre à abscisse négative ou à abscisse positive, ce qui donne a priori quatre cas à étudier.
Cas 1 – \(C\) au dessus de \(A\) et orthocentre à abscisse négative
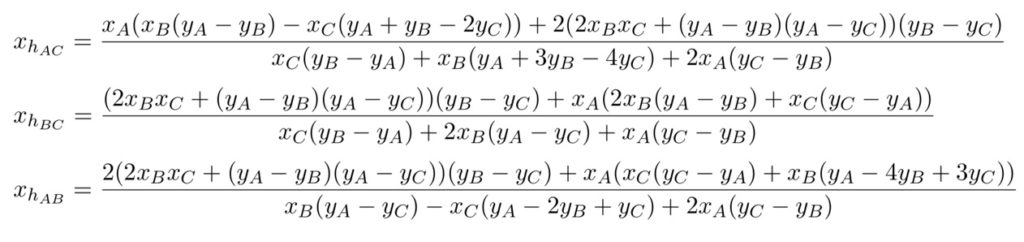
C’est le cas le plus simple à envisager, et il va produire une solution très simple, a priori assez inattendue. Les équations des hauteurs de Moulton donnent pour les abscisses de leurs intersections deux à deux les expressions ci-contre.
L’égalité \(x_{hAC}=x_{hAB}\) aboutit à l’équation factorisée suivante :
\((3x_B-x_C)(y_B-yC)^2(x_A^2+2x_Bx_C-x_A(2x_B+x_C)+(y_A-y_B)(y_A-y_C)) = 0\)
La solution \(x_C=3x_B\) est la solution générale que l’on va mettre en œuvre. L’égalité \(y_B=y_C\) ne correspond pas à la situation. Le troisième terme de la factorisation aboutit à un angle droit en \(A\) car on cherche un orthocentre à abscisse négative.
On a choisit d’écrire le cas \(x_C=3x_B\) sous la forme \(x_B=\frac{x_C}{3}\) (soit \(B\) point construit à partir de \(C\)). La figure est suffisamment générale pour chercher un argument géométrique. La preuve géométrique sera proposée dans le cas dual de cette configuration, un peu plus loin. Elle est néanmoins claire dans l’illustration ci-dessous. La limite de l’ordonnée de \(B\) est le cas où l’orthocentre du triangle est d’abscisse nulle (car on est dans le cas où elle est négative). L’ordonnée \(yMax\) est donnée, elle aussi, par une formule de Type (2) avec les constantes suivantes :
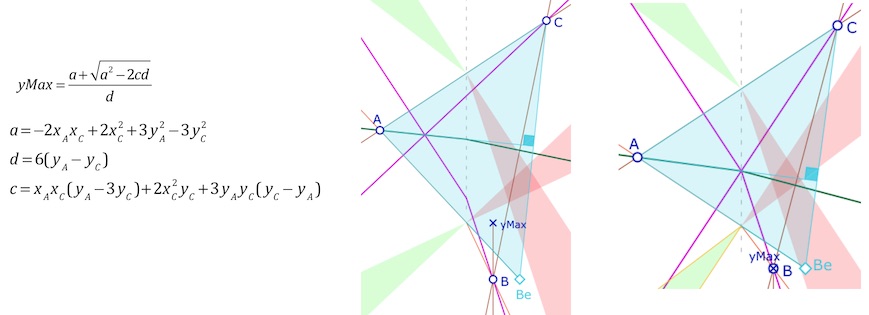
On voit bien l’argument euclidien sur l’illustration du centre. A droite quand \(y_B=yMax\), l’orthocentre se place sur l’axe des ordonnées.
Figure « Triangle orthocentrique avec un seul côté de Moulton à pente négative » (1/2)
On peut agir sur \(A\), \(B\) et \(C\), en respectant les conditions de la figure.
Préférer ouvrir la figure dans un nouvel onglet
Cas 2 – \(C\) au dessus de \(A\) et orthocentre à abscisse positive
On a rassemblé dans une même illustration toutes les données de ce cas : d’abord les coordonnées des intersections des hauteurs prises deux à deux. Ensuite, l’égalité \(x_{hAC}=x_{hAB}\) aboutit à chercher un point en fonction des deux autres. On a choisi, une nouvelle fois, de chercher \(B\) en fonction des deux autres points. On trouve une relation \(y=f(x)\) de Type (2) pour \(B(x, y)\) avec les expressions données ci-dessous.

Le lieu de \(B\) est la courbe de \(f\), bleue ci-dessus. En pratique le «lieu effectif» sur cette courbe est très limité. Il l’est par la zone rouge \(psp_{AC}\) à sa droite et par le point \(B_m \displaystyle \left( \frac{x_C}{3}, f \left( \frac{x_C}{3}\right) \right)\) à sa gauche, point qui correspond à l’orthocentre d’abscisse nulle.
Il n’y a pas à prolonger la courbe bleue au delà de \(psp_{AC}\) (à sa droite) car la perpendiculaire à \((AB)\) issue de \(C\) change de branche sur \((AB)\)et donc d’expression. Le calcul montre qu’il n’y a pas d’orthocentre pour \(B\) au delà de \(psp_{AC}\) dans cette configuration. Par ailleurs chercher le lieu de \(C\) au lieu de celui de \(B\) ne donne pas une plus grande marge puisque le lieu reste limité par la relation \(x_C < 3x_B\) pour que l’orthocentre soit à abscisse positive.
Les valeurs numériques affichées sont celles des valeurs calculées par les relations données ci-dessus.
Sortir \(B\) de la courbe pour vérifier que les valeurs sont bien différentes quand le sommet \(B\) n’est pas sur la courbe.
Préférer ouvrir la figure dans un nouvel onglet
Cas 3 – \(C\) en dessous de \(B\) et orthocentre à abscisse positive
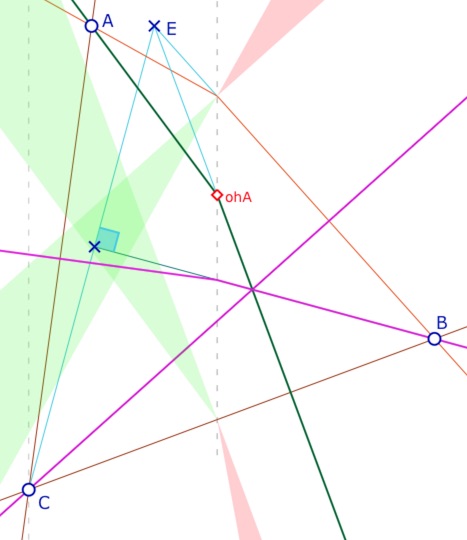
C’est la situation duale du premier cas de cette section que l’on avait traité algébriquement. Nous allons voir une solution géométrique élémentaire qui aurait pu être faite aussi pour la situation précédente.
Soit \(E \displaystyle \left( \frac{x_A}{2}, y_A \right)\). Compte tenu du contexte, les hauteurs de Moulton du triangle \(ABC\) issues de \(C\) et de \(A\) (partie positive) sont les hauteurs euclidiennes du triangle \(EBC\).
Il en résulte qu’il ne peut y avoir un orthocentre pour le triangle de Moulton \(ABC\) que si la hauteur issue de \(B\) pour \(EBC\) coïncide avec la partie positive de la hauteur de \(ABC\) issue de \(B\).
La partie positive de cette hauteur est de pente \(\displaystyle \frac{2(x_C-x_A)}{y_A-y_C}\). Elle est orthogonale à la droite \((EC)\) de pente \(\displaystyle \frac{y_A-y_C}{\frac{x_A}{2}-x_C}\) si et seulement si \(x_C = \frac{3x_A}{2}\).
Impossibilité de triangle bi-orthocentrique dans cette configuration

Quand \(A\) et \(C\) sont placés dans les parties à deux perpendiculaires, on pourrait chercher une configuration qui donnerait un second orthocentre. Voyons que c’est impossible. Soit \(F(2x_B,y_B) \). Les hauteurs de Moulton de \(ABC\) issue de \(B\) et \(C\) sont la hauteur euclidienne issue de \(C\) et la partie positive de la hauteur euclidienne issue de \(F\) du triangle euclidien \(ACF\). Ces droites se coupent en \(h_{ACF}\).
La seule possibilité qu’il y ait un nouvel orthocentre pour \(ABC\) serait que la perpendiculaire à \((CB)\) issue de \(A\) soit aussi perpendiculaire à \((CF)\), ce qui est impossible. Ainsi cette configuration ne permet pas de produire un triangle bi-orthocentrique.
Figure dynamique associée
Penser à mettre \(A\) et \(C\) dans les parties vertes à deux perpendiculaires.
Ouvrir la figure d’un nouvel onglet
Cas 4 – \(C\) en dessous de \(B\) et orthocentre à abscisse négative
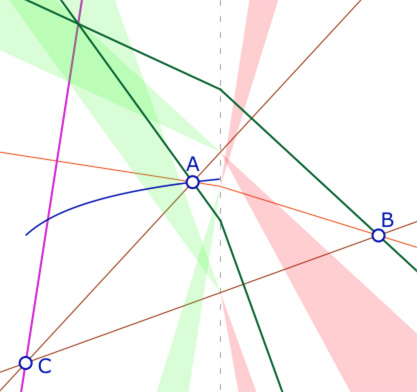
Un orthocentre à abscisse négative implique qu’il soit sur les parties négatives des hauteurs issues de \(A\) et \(B\), et donc que les pieds de ces deux hauteurs (vertes ci-contre) soient à abscisses positives. Les intersections de ces hauteurs ont pour abscisses :
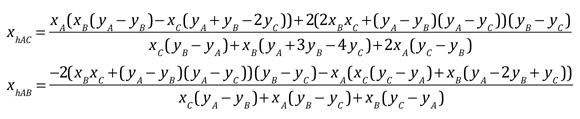
En les égalant, on peut chercher, par exemple, le lieu de \(A(x, y)\) à partir de \(B\) et \(C\). C’est une relation de Type (1) avec les paramètres :
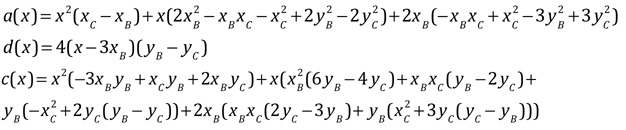
La partie du lieu pour que l’orthocentre existe est entre l’axe des ordonnées et la frontière gauche de la partie à deux perpendiculaires pour la droite \((BC)\). Au delà, ce n’est plus la même perpendiculaire issue de \(A\).
A l’ouverture, le point \(A\) n’est pas sur la courbe, il n’y a donc pas d’orthocentre.
En plaçant \(A\) sur la courbe, on vérifie que les valeurs numériques deviennent égales.
Préférer ouvrir la figure dans un nouvel onglet