Contrairement aux pages de géométrie hyperbolique dans le disque de Poincaré (menu DP) ou aux pages de géométrie elliptique (menu Ell) conçues comme une découverte non technique, avec les outils appropriés sous forme de macro-construction, nous donnerons ici plus d’éléments techniques de réalisation, car la pseudosphère est moins documentée sur les réseaux. Le lecteur aura donc droit à un petit formulaire pseudosphérique. On peut aussi se centrer simplement sur les figures sans entrer dans les détails techniques.
Milieu
Coordonnées du milieu I de deux points A et B.
La longitude \(\theta_I\) est donnée par cette « formule de la moyenne » \(\displaystyle th^{-1} \left(\frac{\theta_I+c_{AB}}{k_{AB}}\right)=\displaystyle \frac{th^{-1} \left(\frac{\theta_A+c_{AB}}{k_{AB}}\right)+th^{-1} \left(\frac{\theta_B+c_{AB}}{k_{AB}}\right)}{2}\).
Ensuite le point \(I\) est placé sur la droite car on connaît sa longitude et les constantes de la droite \((AB)\).
On peut donc déjà construire l’intersection des médianes d’un triangle.
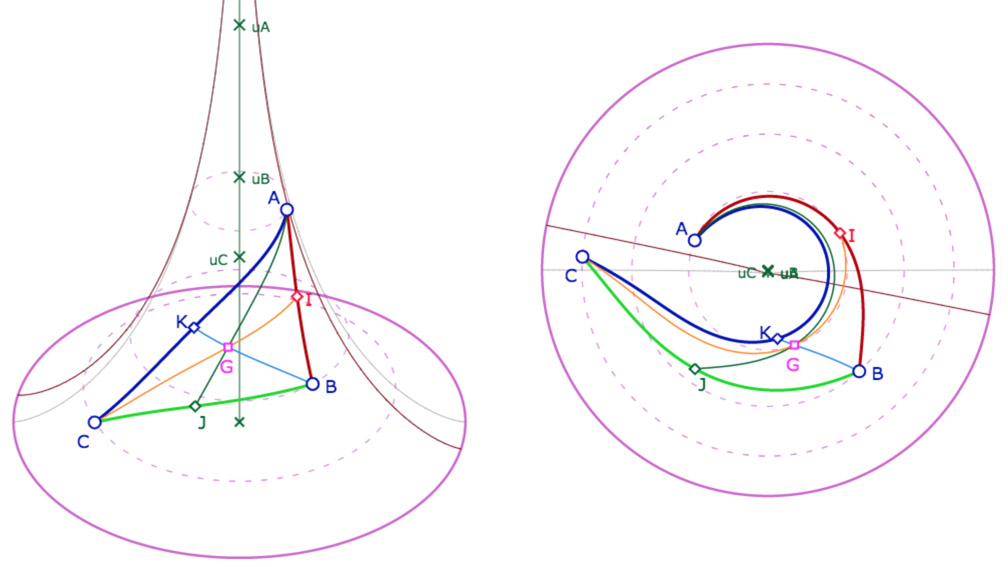
Deux illustrations que les médianes sont concourantes. Dans les deux cas tous les points sont sur la feuille principale
Manipulation de la figure
On peut déplacer les sommets du triangle par leur altitude ou leur longitude, mais aussi changer la feuille de chaque point.
Penser à tourner la pseudosphère
L’intersection de deux droites se fait directement à partir de leurs constantes : ce n’est qu’une résolution d’une équation à une inconnue \(\theta_{Inter}\), longitude que l’on replace sur une des des deux droites depuis ses constantes.
Symétrie centrale
La symétrie centrale peut s’obtenir sans calcul, depuis la « formule de la moyenne » précédente. En effet si on écrit, formellement, comme dans le cas affine \(\displaystyle I = \frac{A+B}{2}\), alors clairement, le symétrique \(B\) de \(A\) par rapport à \(I\) s’écrit aussi \(B=2I-A\), ce qui donne automatiquement la longitude \(\theta_B\) du symétrique : \(\displaystyle th^{-1} \left(\frac{\theta_B+c_{IA}}{k_{IA}}\right)=\displaystyle 2th^{-1} \left(\frac{\theta_I+c_{IA}}{k_{IB}}\right)-th^{-1} \left(\frac{\theta_A+c_{IB}}{k_{IB}}\right)\)
Cette symétrie par rapport à un point permettra de construire, toujours sans calculs supplémentaires, l’image d’un point par une symétrie orthogonale une fois qu’on aura traité de l’orthogonalité.
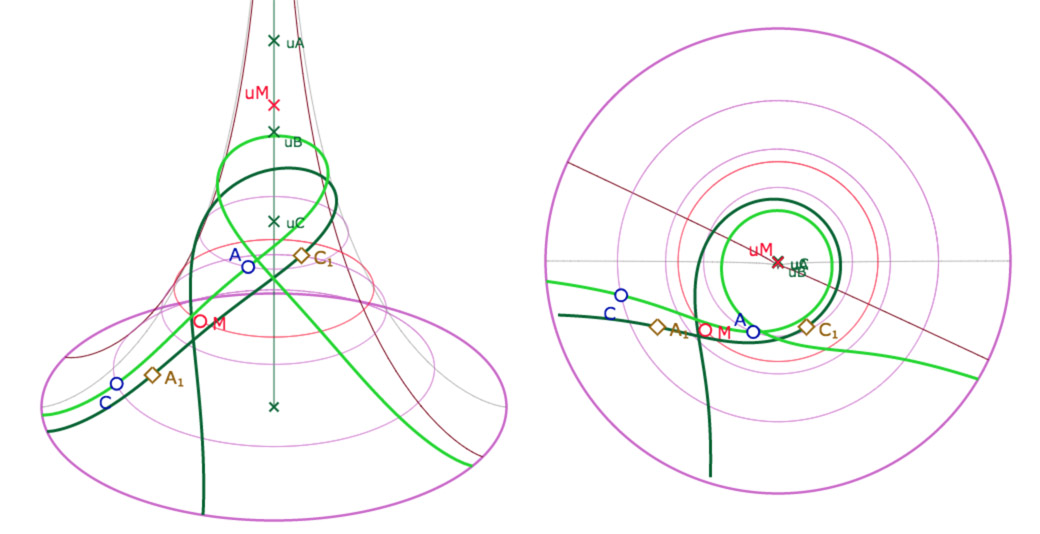
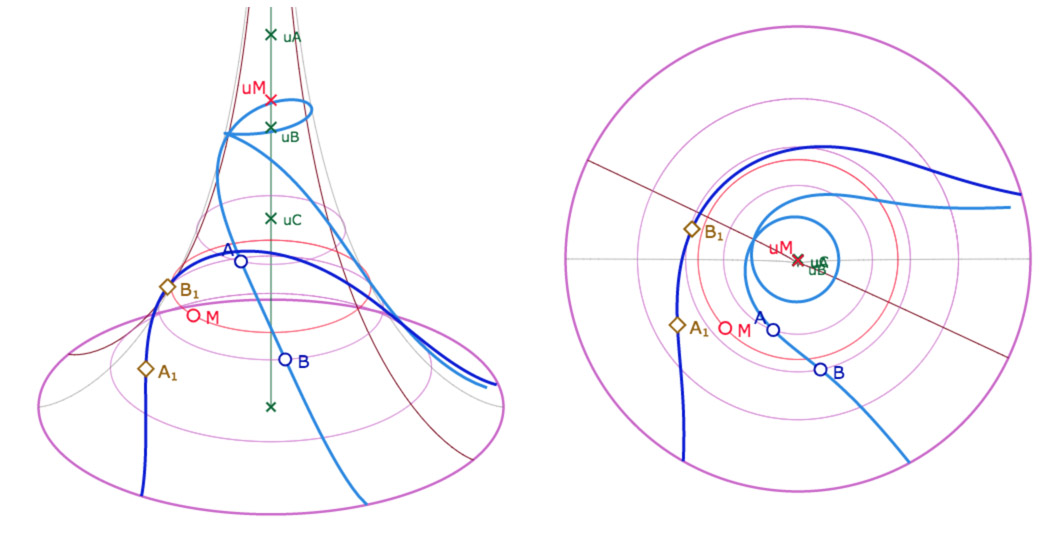
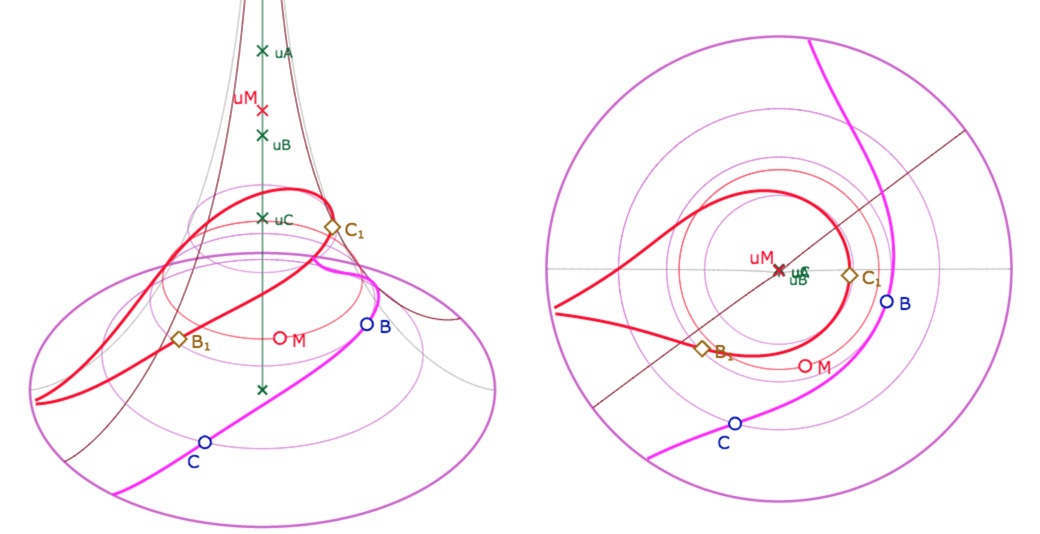
Voici quelques illustrations de la figure suivante : on peut manipuler trois points \(A, B, C\) et un point \(M\) par leurs longitudes et latitudes. La figure construit les points \(A_1, B_1, C_1\), les symétriques des premiers par rapport à \(M\).
Galerie de quatre illustrations de la figure suivante
La figure associée
Rappel : on glisse simplement la souris enfoncée ou le doigt vers le bas sur la figure pour passer progressivement en mode « vue de dessus ».
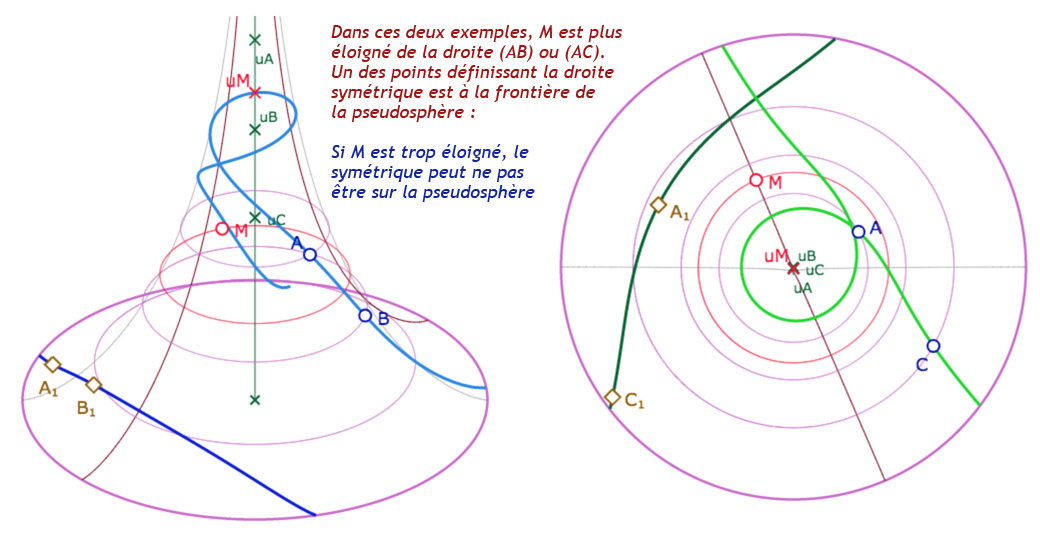
Manipuler les 4 points \(A, B, C\)et \(M\). Attention à ce que le symétrique ne sorte pas de la surface :
en effet, la pseudosphère n’est qu’une représentation locale du plan hyperbolique.